DIGITAL IMAGE PROCESSING IMAGE COMPRESSION Introduction q Image































- Slides: 41

DIGITAL IMAGE PROCESSING IMAGE COMPRESSION

Introduction q Image Compression: It is the Art & Science of reducing the amount of data required to represent an image. q It is the most useful and commercially successful technologies in the field of Digital Image Processing. q The number of images compressed and decompressed daily is innumerable.

Introduction q To understand the need for compact image representation, consider the amount of data required to represent a 2 hour Standard Definition (SD) using 720 x 480 x 24 bit pixel arrays. q A video is a sequence of video frames where each frame is a full color still image. q Because video player must display the frames sequentially at rates near 30 fps, SD video data must be accessed at 30 fps x (720 x 480)ppf x 3 bpp = 31, 104, 000 bps fps – frames per second, ppf – pixels per frame, bpp – bytes per pixel & bps – bytes per second

Introduction Thus a 2 hour movie consists of 31, 104, 000 bps x (602) sph x 2 hrs ≈ 2. 24 OR sph = second per hour x 1011 bytes. 224 GB of data q Twenty seven 8. 5 GB dual layer DVDs are needed to store it. q To put a 2 hr movie on a single DVD, each frame must be compressed by a factor of around 26. 3. q The compression must be even higher for HD, where image resolution reach 1920 x 1080 x 24 bits/image.

Introduction q Web page images & High-resolution digital camera photos also are also compressed to save storage space & reduce transmission time. q Residential Internet connection delivers data at speeds ranging from 56 kbps (conventional phone line) to more than 12 mbps (broadband). q Time required to transmit a small 128 x 24 bit full color image over this range of speed is from 7. 0 to 0. 03 sec. q Compression can reduce the transmission time by a factor of around 2 to 10 or more. q Similarly, number of uncompressed full color images that an 8 Megapixel digital camera can store on a 1 GB Memory card can be increased.

Introduction q Along with these applications , image compression plays an important role in many other areas including:

Fundamentals q Data Compression: It refers to the process of reducing the amount of data required to represent a given quantity of information. Data Vs Information q Data and Information are not the same thing; data are the means by which information is conveyed. q Because various amount of data can be used to represent the same amount of information, representations that contain irrelevant or repeated information are said to contain redundant data.

Fundamentals

Fundamentals q Let b & b’ denote the number of bits in two representations of the same information, the relative data redundancy R of the representation with b bits is • R = 1 – (1/C); where, C commonly called the compression ratio, is defined as • C = b / b’ q If C = 10 (or 10: 1), for larger representation has 10 bits of data for every 1 bit of data in smaller representation. So, R = 0. 9, indicating that 90% of its data is redundant.

Fundamentals q 2 D intensity arrays suffers from 3 principal types of data redundancies: 1) Coding redundancy: A code is a system of symbols used to represent a body of information or sets of events. q Each piece of event is assigned a code word (code symbol). The number of symbols in each code word is its length. q The 8 -bit codes that are used to represent the intensities in most 2 D intensity arrays contain more bits than are needed to represent the intensities.

Fundamentals 2) Spatial & Temporal redundancy: q Because the pixels of most 2 D intensity arrays are correlated spatially, information is replicated unnecessarily. q In video sequence, temporally correlated pixels also duplicate information. 3) Irrelevant Information: q Most 2 D intensity arrays contain information that is ignored by the human visual system. It is redundant in the sense that it is not used.

Fundamentals 1) Coding Redundancy: § Assume a discrete random variable rk in interval [0 – L-1] is used to represent the intensities of an M x N image. § Also the each rk occurs with probability pr (rk). § pr(rk) = nk / MN k = 0, 1, 2, …………. L-1 -----(a) § Where, L is no. of intensity values & nk is no. of times kth intensity appears in the image. If no. of bits used to represent each value of rk is l(rk), then avg no of bits required to represent each pixel is L-1 Lavg = Σ l(rk) pr(rk) k=0 Thus, total no. of bits required to represent an Mx. N image is MNLavg.

Fundamentals § § § If the intensities are represented using a natural m-bits fixed length code, the RHS reduces to m bits. i. e. Lavg = m where m is substituted for l(rk). Constant m can be taken out the summation leaving only sum of pr(rk) for 0 ≤ k ≤ L-1, which = 1. rk pr(rk) r 87 = 87 0. 25 r 128 = 128 0. 47 r 186 = 186 0. 25 r 255 = 255 0. 03 rk for k ≠ 87, 0 128, 186, 255 code 1 l 1(rk) 01010111 8 10000000 8 11000100 8 1111 8 8 code 2 l 2(rk) 01 2 1 1 000 3 001 3 0

Fundamentals With respect to the above table, If a natural 8 -bit binary code is used to represent its 4 possible intensities, Lavg = 8, coz l 1(rk) = 8 bits for all rk. On the other hand, If code 2 scheme is used, the avg length of encoded pixels is, Lavg = 0. 25(2) + 0. 47(1) + 0. 25(3) + 0. 03(3) = 1. 81 bits. Total no. of bits rqd to represent entire image = MNLavg = 256 x 1. 81 = 118, 621 Resulting compression C = 256 x 8 / 118, 621 = 8 / 1. 81 ≈ 4. 42 Relative redundancy R = 1 – 1/4. 42 = 0. 774 Thus, 77. 4% of data in original 8 -bit 2 D intensity array is redundant.

Fidelity Criteria: • Removal of irrelevant visual information involves a loss of real or quantitative image information. • Since information is lost, a means of quantifying the nature of loss is needed. Objective fidelity criteria Subjective fidelity criteria Ø Objective fidelity criteria: When information loss can be expressed as a mathematical function of input & output of a compression process. Eg RMS error between 2 images. Error between two images e(x, y) = f’(x, y) – f(x, y) So, total error between two images M-1 N-1 Σ Σ [f’(x, y) – f(x, y)] x=0 y = 0

Fidelity Criteria RMS error is given by M-1 N-1 erms = [(1/MN)Σ Σ [f’(x, y) – f(x, y)]2]1/2 x=0 y = 0 If f’(x, y) is considered to be the sum of original image f(x, y) & an error or noise signal e(x, y), the Mean Square SNR of output image denoted by SNRrms can be defined as M-1 N-1 SNRrms = Σ Σ f’(x, y)2 x=0 y = 0 M-1 N-1 Σ Σ [f’(x, y) – f(x, y)]2 x=0 y = 0

Fidelity Criteria Ø Subjective fidelity criteria: • A Decompressed image is presented to a cross section of viewers and averaging their evaluations. • • It can be done by using an absolute rating scale Or By means of side by side comparisons of f(x, y) & f’(x, y). Side by Side comparison can be done with a scale such as {-3, -2, -1, 0, 1, 2, 3} to represent the subjective valuations {much worse, slightly worse, the same, slightly better, much better} respectively. •

Image Compression Models • The image compression system is composed of 2 distinct functional component: an encoder & a decoder. • Encoder performs Compression while Decoder performs Decompression. • • Both operations can be performed in Software, as in case of Web browsers & many commercial image editing programs. • Or in a combination of hardware & firmware, as in DVD Players. • A codec is a device which performs coding & decoding.

Image Compression Models • Input image f(x, …. . ) is fed into the encoder, which creates a compressed representation of input. • It is stored for future for later use or transmitted for storage and use at a remote location. • When the compressed image is given to decoder, a reconstructed output image f’(x, …. . ) is generated. • In still image applications, the encoded input and decoder output are f(x, y) & f’(x, y) resp. • In video applications, they are f(x, y, t) & f’(x, y, t) where t is time. • If both functions are equal then the system is called lossless, error free. If not then it s referred to as lossy.

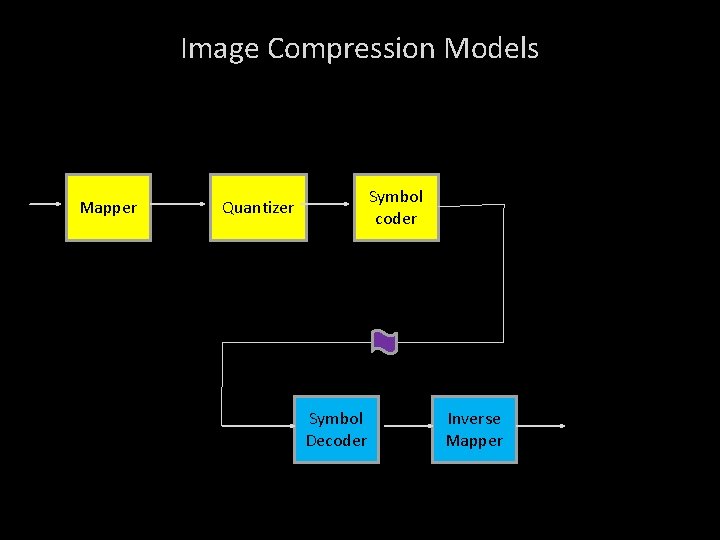
Image Compression Models Mapper Symbol coder Quantizer Symbol Decoder Inverse Mapper

Image Compression Models Encoding or Compression process: Encoder is used to remove the redundancies through a series of 3 independent operations. Mapper: It transforms f(x, …) into a format designed to reduce spatial and temporal redundancies. • It is reversible • It may / may not reduce the amount of data to represent image. Ex. Run Length coding • In video applications, mapper uses previous frames to remove temporal redundancies.

Image Compression Models Quantizer: It keeps irrelevant information out of compressed representations. • This operation is irreversible. • It must be omitted when error free compression is desired. • In video applications, bit rate of encoded output is often measured and used to adjust the operation of the quantizer so that a predetermined average output is maintained. • The visual quality of the output can vary from frame to frame as a function of image content.

Image Compression Models Symbol Encoder: Generates a fixed or variable length code to represent the quantizer output and maps the output in accordance with the code. • Shortest code words are assigned to the most frequently occurring quantizer output values. Thus minimizing coding redundancy. • It is reversible. • Upon its completion, the input image has been processed for the removal of all 3 redundancies.

Image Compression Models Decoding or Decompression process: • Quantization results in irreversible loss, an inverse quantizer block is not included in the decoder block.

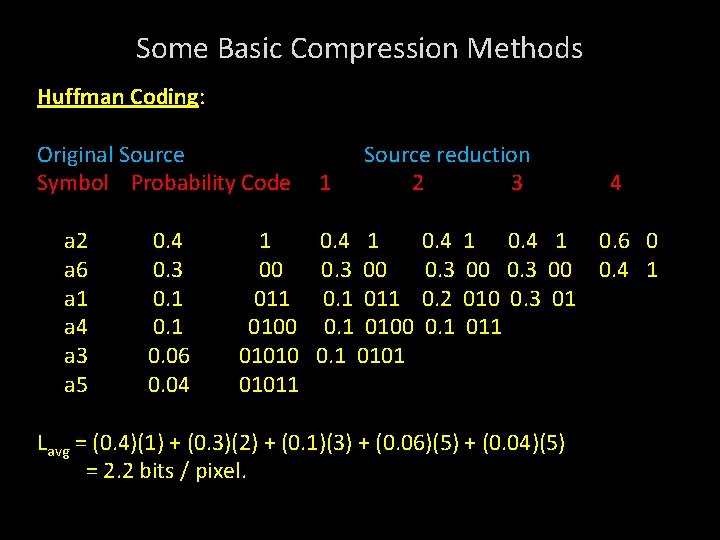
Some Basic Compression Methods Huffman Coding: • Most popular technique for removing coding redundancies. • It yields smallest possible code symbol per source symbol. Original Source Symbol Probability a 2 a 6 a 1 a 4 a 3 a 5 0. 4 0. 3 0. 1 0. 06 0. 04 Source reduction 1 2 3 0. 4 0. 3 0. 1 0. 4 0. 3 0. 2 0. 1 0. 4 0. 3 4 0. 6 0. 4

Some Basic Compression Methods Huffman Coding: Original Source Symbol Probability Code a 2 a 6 a 1 a 4 a 3 a 5 0. 4 0. 3 0. 1 0. 06 0. 04 1 00 011 0100 01011 1 Source reduction 2 3 0. 4 1 0. 3 00 0. 1 011 0. 1 0100 0. 1 0101 0. 4 0. 3 0. 2 0. 1 4 1 0. 6 0 00 0. 3 00 0. 4 1 010 0. 3 01 011 Lavg = (0. 4)(1) + (0. 3)(2) + (0. 1)(3) + (0. 06)(5) + (0. 04)(5) = 2. 2 bits / pixel.

Some Basic Compression Methods Huffman Coding: • It is instantaneous. • Coz each code word in a string of code symbols ca be decoded without referencing succeeding symbols. • • It is uniquely decodable. Coz any string of code symbols can be decoded by examining individual symbols of string from left to right. Ex. 010100111100

Some Basic Compression Methods Huffman Coding: • It is instantaneous. • Coz each code word in a string of code symbols ca be decoded without referencing succeeding symbols. • • It is uniquely decodable. Coz any string of code symbols can be decoded by examining individual symbols of string from left to right. Ex. 01010 011 1 1 00 First valid code: 01010 – a 3, 011 – a 1, Thus, completely decoding the message, we get, a 3 a 1 a 2 a 2 a 6

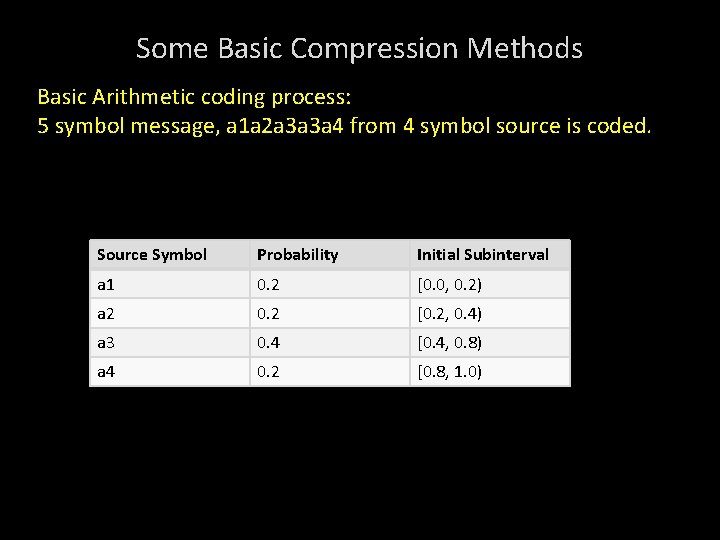
Some Basic Compression Methods Arithmetic coding: It generates non block codes. One to One correspondence between source symbols and code words does not exist. Instead, an entire sequence of source symbols is assigned a single arithmetic code. Code word defines an integer of real numbers between 0 & 1. As No. of symbols in msg. interval to represent it no. of bits to represent info Each symbol of msg size of interval in accordance with its probability of occurrence.

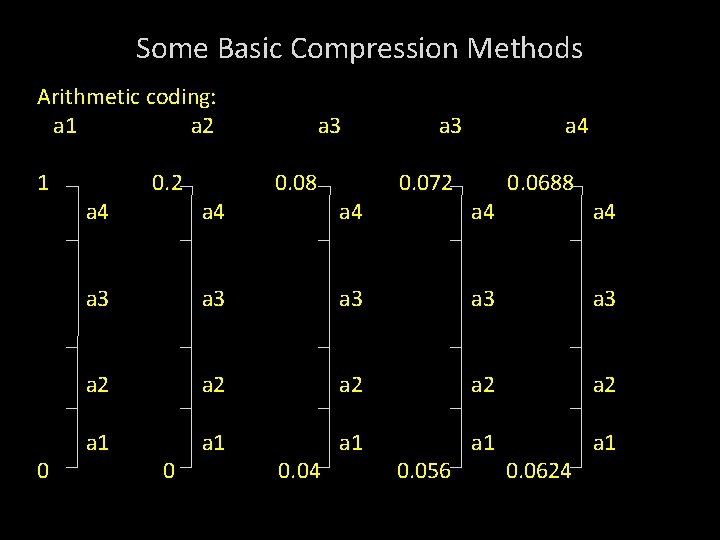
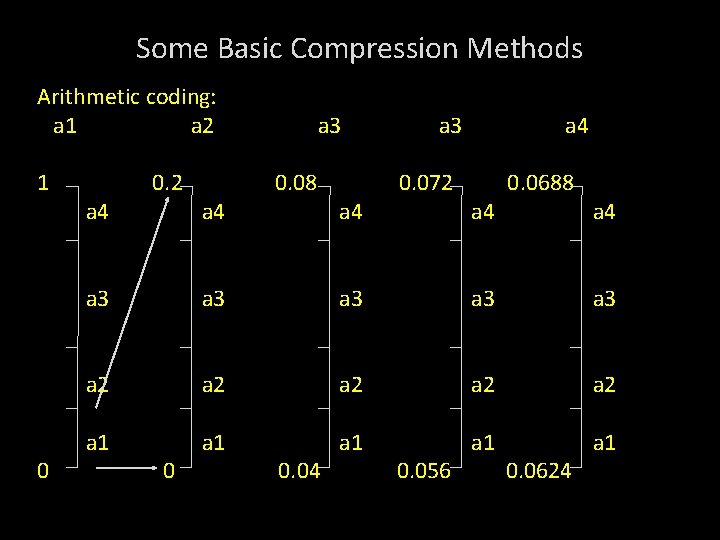
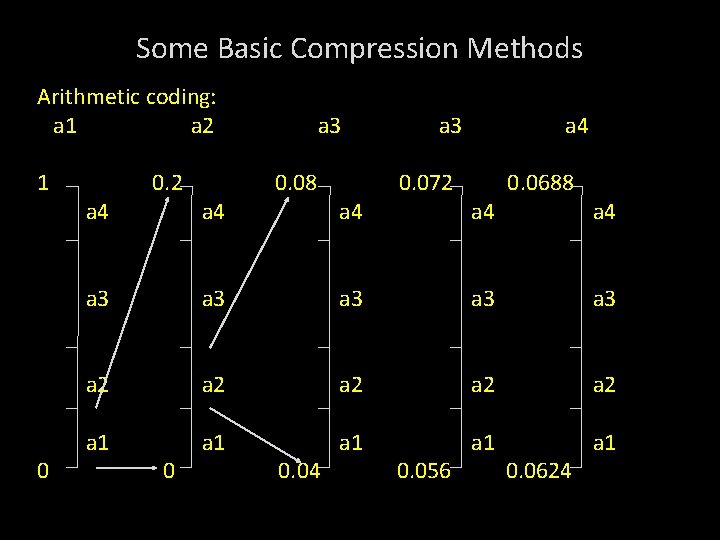
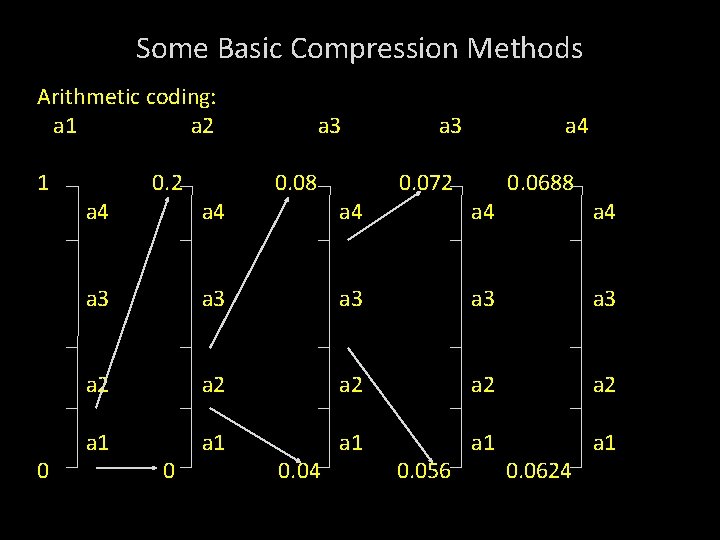
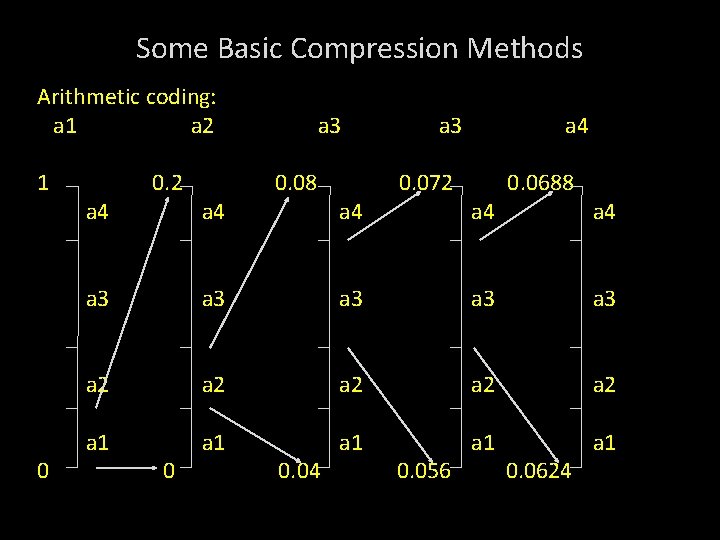
Some Basic Compression Methods Basic Arithmetic coding process: 5 symbol message, a 1 a 2 a 3 a 3 a 4 from 4 symbol source is coded. Source Symbol Probability Initial Subinterval a 1 0. 2 [0. 0, 0. 2) a 2 0. 2 [0. 2, 0. 4) a 3 0. 4 [0. 4, 0. 8) a 4 0. 2 [0. 8, 1. 0)

Some Basic Compression Methods Arithmetic coding: a 1 a 2 1 0 a 4 0. 2 a 4 a 3 0. 08 a 4 a 3 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

Some Basic Compression Methods Arithmetic coding: a 1 a 2 1 0 a 4 0. 2 a 4 a 3 0. 08 a 4 a 3 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

Some Basic Compression Methods Arithmetic coding: a 1 a 2 1 0 a 4 0. 2 a 4 a 3 0. 08 a 4 a 3 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

Some Basic Compression Methods Arithmetic coding: a 1 a 2 1 0 a 4 0. 2 a 4 a 3 0. 08 a 4 a 3 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

Some Basic Compression Methods Arithmetic coding: a 1 a 2 1 0 a 4 0. 2 a 4 a 3 0. 08 a 4 a 3 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

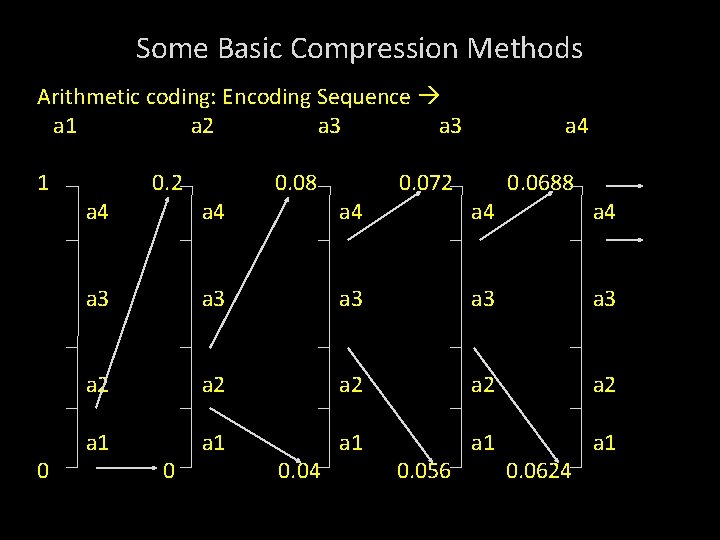
Some Basic Compression Methods Arithmetic coding: Encoding Sequence a 1 a 2 a 3 1 0 a 4 0. 2 a 4 0. 08 a 4 0. 072 a 4 0. 0688 a 4 a 3 a 3 a 3 a 2 a 2 a 2 a 1 a 1 a 1 0 0. 04 0. 056 0. 0624

Some Basic Compression Methods The final message symbol narrows to [0. 06752, 0. 0688). Any number between this interval can be used to represent the message. Eg. 0. 068 3 decimal digits are used to represent the 5 symbol message.

Some Basic Compression Methods Bit-plane coding: q Another effective method to reduce interpixel redundancies. q Image’s bit planes are processed individually. q Based on decomposing a multilevel (monochrome / color) image into a series of binary images & compressing each binary using any binary compression method. Bit plane decomposition: q Gray levels of an m-bit gray level image can be represented in form of base 2 polynomial. am-12 m-1+am-22 m-2+……. . +a 121+a 020 ………(1)

Some Basic Compression Methods § A simple method of decomposing the image into a collection of binary image is to separate the m coefficients of the polynomial into m-1 bit planes. Disadvantage: § Small changes in gray level can have significant impact on complexity of bit planes. Ex. If two adjacent pixels have intensity of 127 (01111111) and 128 (10000000), every bit plane will contain a corresponding 0 to 1 (or 1 to 0) transition.

Some Basic Compression Methods Alternate decomposition approach: § Reduces the effect of small gray level variations. § Requires the representation of image into m-bit gray code. § m-bit gray code gm-1…. . g 2 g 1 g 0 can be computed from gi = ai xor ai+1 0 ≤ i ≤ m-2 gm-1 = am-1 § This code has unique property that successive code words differ by only 1 bit position. Small changes in gray level are less likely to affect all m bit planes. Ex. 127 (11000000) & 128 (01000000). §

Some Basic Compression Methods Run-Length Coding: § Standard compression approach used in facsimile (FAX). § Basic concept is to code each contiguous group of 0’s & 1’s encountered in L to R scan of a row by its length & to develop a convention for determining the value of run. § Most common approach for determining the value of run: i) Specify value of first run of each row. ii) To assume each row begins with a white run whose run length may in fact be zero.