DIGITAL IMAGE PROCESSING Part I Image Transforms 1

DIGITAL IMAGE PROCESSING Part I: Image Transforms

1 -D SIGNAL TRANSFORM GENERAL FORM • Scalar form • Matrix form

1 -D SIGNAL TRANSFORM cont. REMEMBER THE 1 -D DFT!!! • General form • DFT

1 -D INVERSE SIGNAL TRANSFORM GENERAL FORM • Scalar form • Matrix form

1 -D INVERSE SIGNAL TRANSFORM cont. REMEMBER THE 1 -D DFT!!! • General form • DFT

1 -D UNITARY TRANSFORM • Matrix form

SIGNAL RECONSTRUCTION

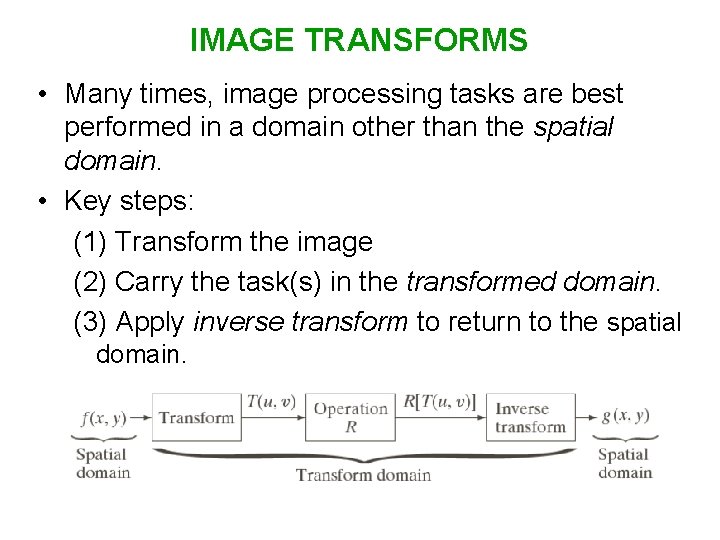
IMAGE TRANSFORMS • Many times, image processing tasks are best performed in a domain other than the spatial domain. • Key steps: (1) Transform the image (2) Carry the task(s) in the transformed domain. (3) Apply inverse transform to return to the spatial domain.

2 -D (IMAGE) TRANSFORM GENERAL FORM

2 -D IMAGE TRANSFORM SPECIFIC FORMS • Separable • Symmetric

• Separable and Symmetric • Separable, Symmetric and Unitary

ENERGY PRESERVATION • 1 -D • 2 -D

ENERGY COMPACTION Most of the energy of the original data concentrated in only a few of the significant transform coefficients; remaining coefficients are near zero.

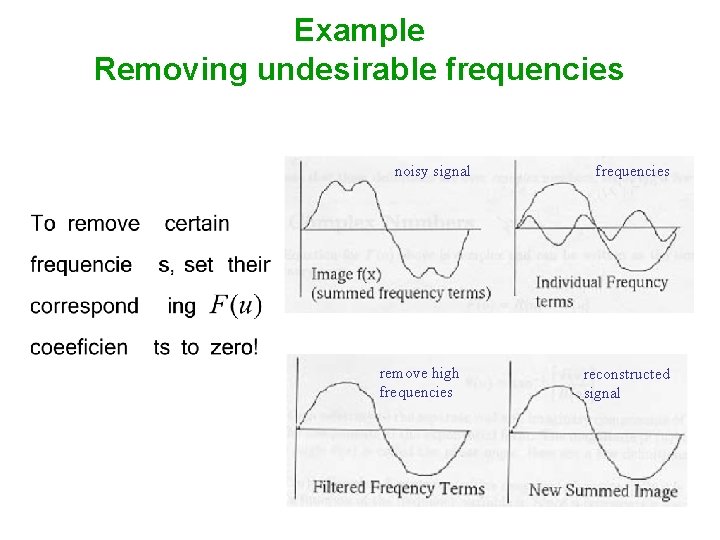
Why is Fourier Transform Useful? • Easier to remove undesirable frequencies. • Faster to perform certain operations in the frequency domain than in the spatial domain. • The transform is independent of the signal.

Example Removing undesirable frequencies noisy signal remove high frequencies reconstructed signal

How do frequencies show up in an image? • Low frequencies correspond to slowly varying information (e. g. , continuous surface). • High frequencies correspond to quickly varying information (e. g. , edges) Original Image Low-passed

2 -D DISCRETE FOURIER TRANSFORM

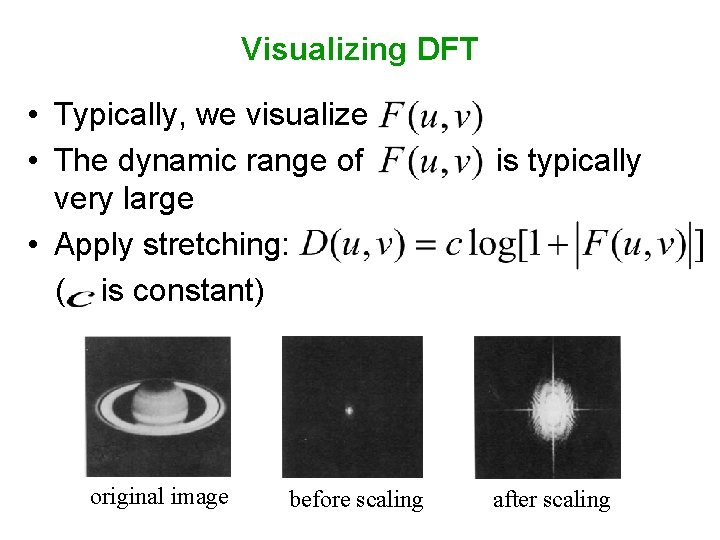
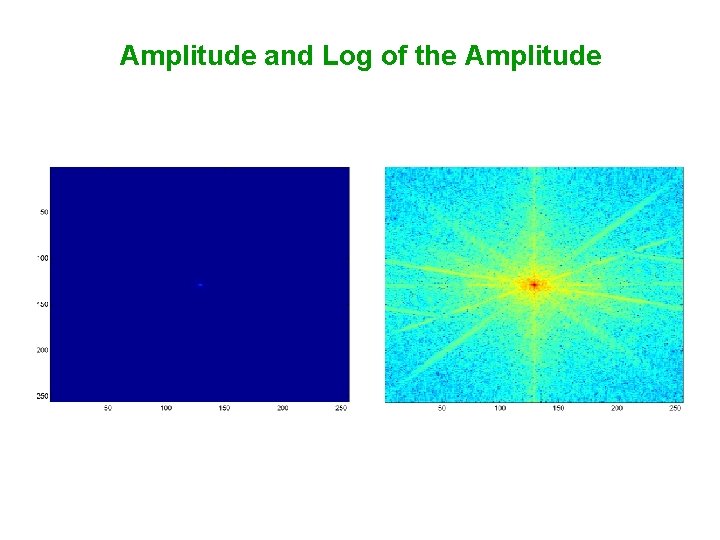
Visualizing DFT • Typically, we visualize • The dynamic range of very large • Apply stretching: ( is constant) original image before scaling is typically after scaling

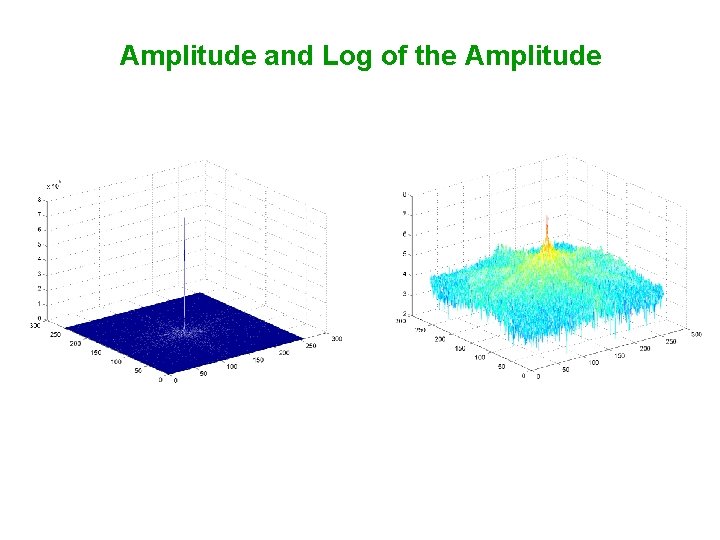
Amplitude and Log of the Amplitude

Amplitude and Log of the Amplitude

Original and Amplitude

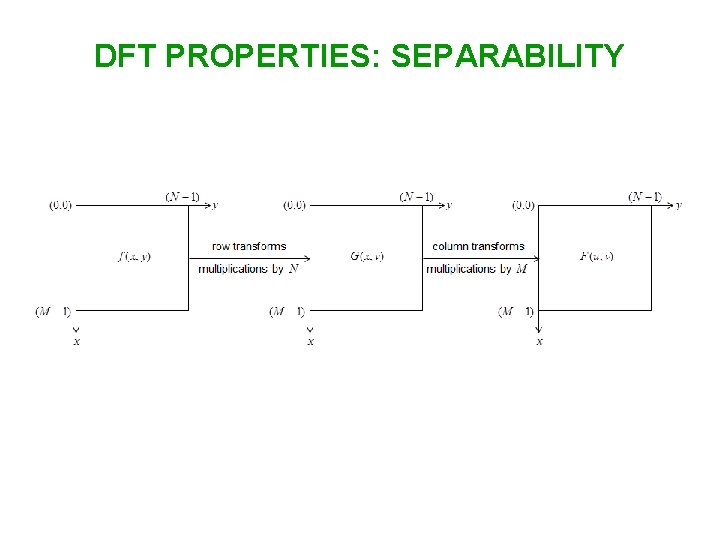
DFT PROPERTIES: SEPARABILITY Rewrite If we set: Then: as follows:

DFT PROPERTIES: SEPARABILITY • How can we compute ?

DFT PROPERTIES: SEPARABILITY

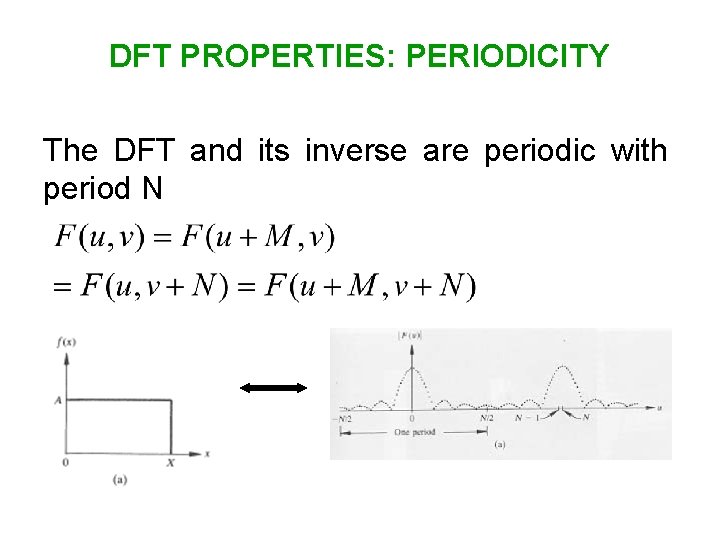
DFT PROPERTIES: PERIODICITY The DFT and its inverse are periodic with period N

DFT PROPERTIES: SYMMETRY If is real, then

DFT PROPERTIES: TRANSLATION • Translation in spatial domain: • Translation in frequency domain:

DFT PROPERTIES: TRANSLATION Warning: to show a full period, we need to translate the origin of the transform at

DFT PROPERTIES: TRANSLATION

DFT PROPERTIES: TRANSLATION no translation after translation

DFT PROPERTIES: ROTATION

DFT PROPERTIES ADDITION-MULTIPLICATION

DFT PROPERTIES: SCALE

DFT PROPERTIES: AVERAGE

Original Image Fourier Amplitude Fourier Phase

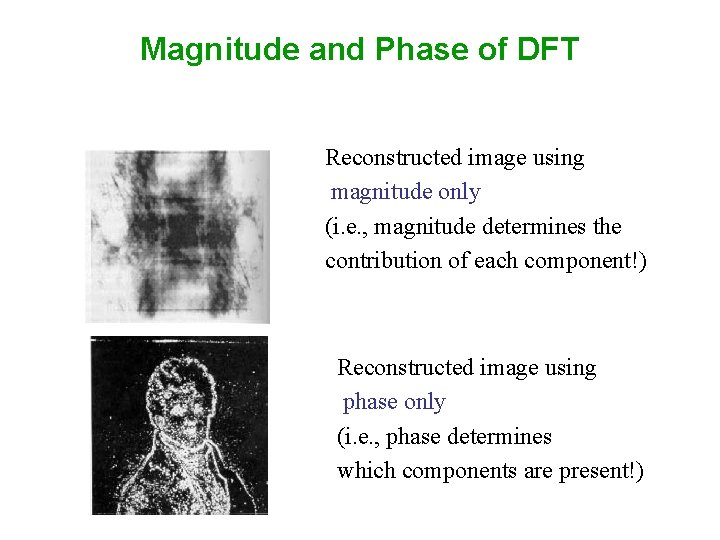
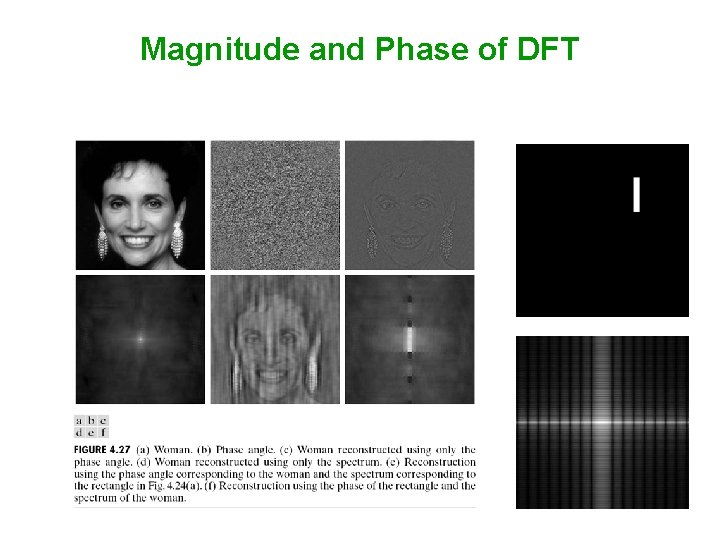
Magnitude and Phase of DFT • What is more important? magnitude phase • Hint: use inverse DFT to reconstruct the image using magnitude or phase only information

Magnitude and Phase of DFT Reconstructed image using magnitude only (i. e. , magnitude determines the contribution of each component!) Reconstructed image using phase only (i. e. , phase determines which components are present!)

Magnitude and Phase of DFT

Original Image-Fourier Amplitude Keep Part of the Amplitude Around the Origin and Reconstruct Original Image (LOW PASS filtering)

Keep Part of the Amplitude Far from the Origin and Reconstruct Original Image (HIGH PASS filtering)

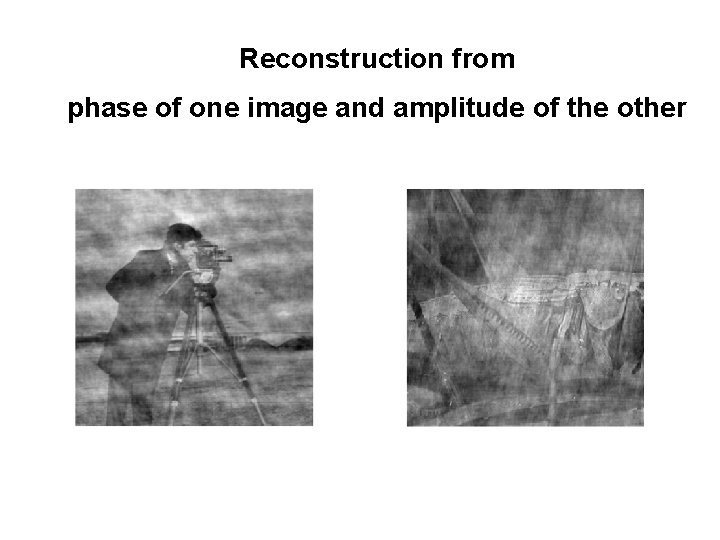
Reconstruction from phase of one image and amplitude of the other

Reconstruction from phase of one image and amplitude of the other