Natural Homogeneous Coordinates In projective geometry parallel lines

Natural Homogeneous Coordinates Ø In projective geometry parallel lines intersect at a point. • The point at infinity is called an ideal point. • There is an ideal point for every slope. • The collection of ideal points is called an ideal line. • We might think of the line as a circle.

Representing Points in the Projective Plane Ø A coordinate pair (x, y) is not sufficient to represent both ordinary points and ideal points. Ø We use triples, (x, y, z), to represent points in the projective plane

Representing Ideal Points Using Triples: (x, y, z) Ø Consider two distinct parallel lines: • ax + by + cz = 0 • ax + by + c'z = 0 (c not equal to c') • (c - c') * z = 0 hence z = 0. Ø We use z=0 to represent ideal points.

Projective Coordinate Triples And Cartesian Coordinate Pairs • Let z = 1. – Then a projective coordinate line given by ax + by +cz=0 becomes ax + by + c = 0. – The second equation corresponds to the equation of a line in Euclidean coordinates. – We can make the correspondence between points (x, y, 1) in parallel coordinates and points (x, y) in Euclidean coordinates

Projective Points And Euclidean Points • If a point ( x, y, 1) is on the line ax + by + cz=0, so is point (px, py, p) for any p. Note: apx + bpy + cpz = p * (ax + by + cz)=0 • Multiple projective coordinate points correspond to the same Euclidean coordinate. • To obtain Euclidean coordinates from non-ideal points represented as projective coordinates, divide by the last coordinate so it becomes 1.

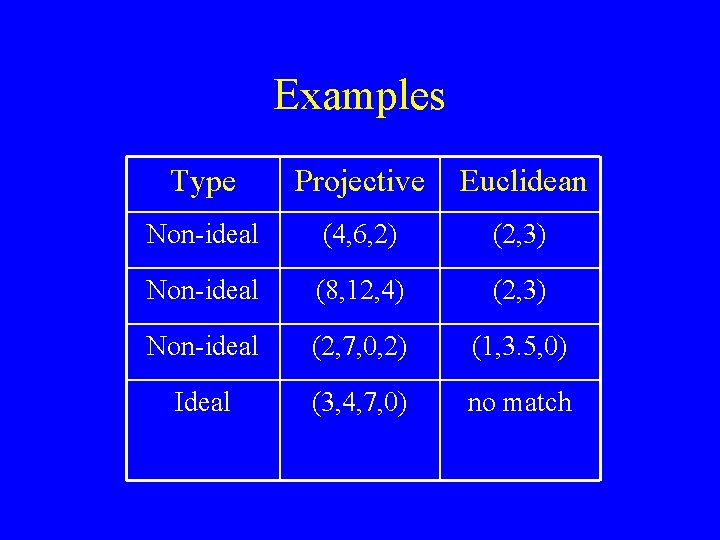
Examples Type Projective Euclidean Non-ideal (4, 6, 2) (2, 3) Non-ideal (8, 12, 4) (2, 3) Non-ideal (2, 7, 0, 2) (1, 3. 5, 0) Ideal (3, 4, 7, 0) no match