GEOMETRY Angles and Parallel Lines Intersecting Lines Lines

GEOMETRY Angles and Parallel Lines

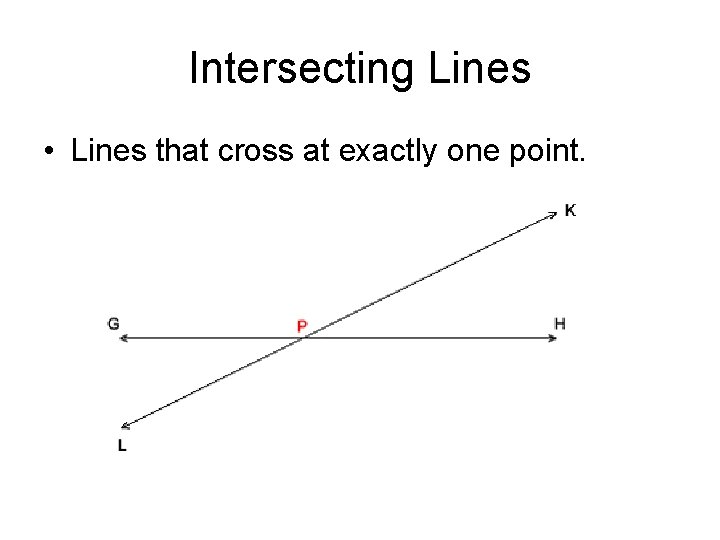
Intersecting Lines • Lines that cross at exactly one point.

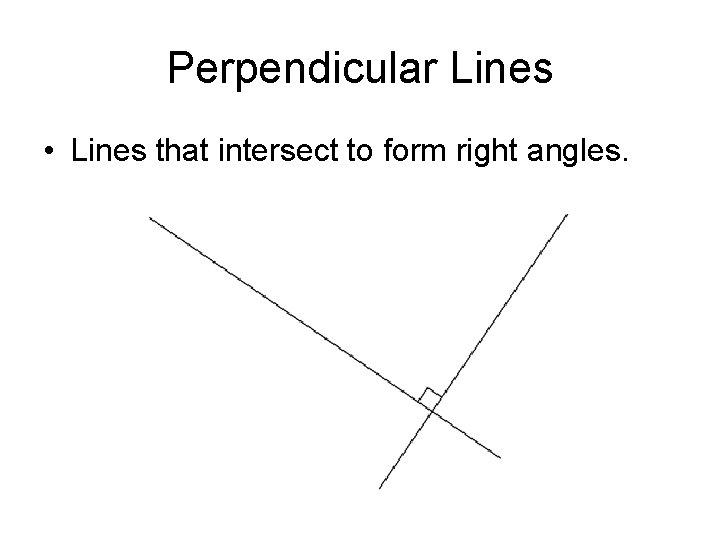
Perpendicular Lines • Lines that intersect to form right angles.

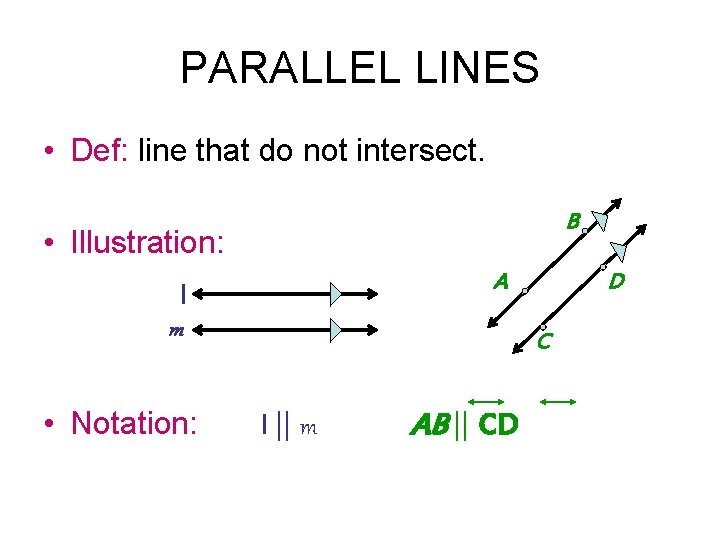
PARALLEL LINES • Def: line that do not intersect. B • Illustration: A l m • Notation: D C l || m AB || CD

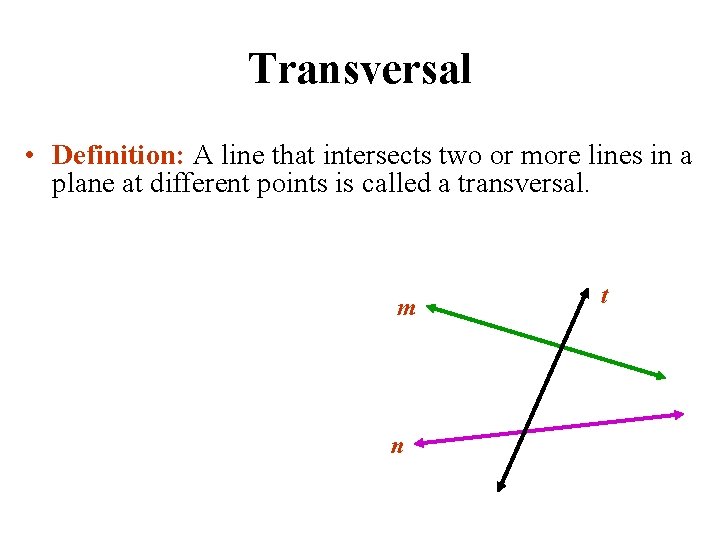
Transversal • Definition: A line that intersects two or more lines in a plane at different points is called a transversal. m n t

Vertical Angles & Linear Pair Vertical Angles: Two angles that are opposite angles. Vertical angles are congruent. 1 4, 2 3, 5 8, 6 7 Linear Pair: Supplementary angles that form a line (sum = 180 ) 1 & 2 , 2 & 4 , 4 & 3, 3 & 1, 5 & 6, 6 & 8, 8 & 7, 7 & 5 1 3 4 5 7 6 8 2

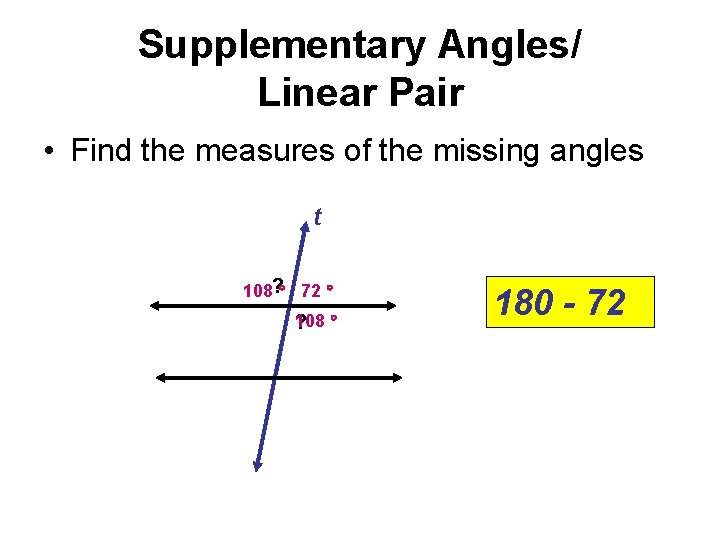
Supplementary Angles/ Linear Pair • Find the measures of the missing angles t 108? 72 108 ? 180 - 72

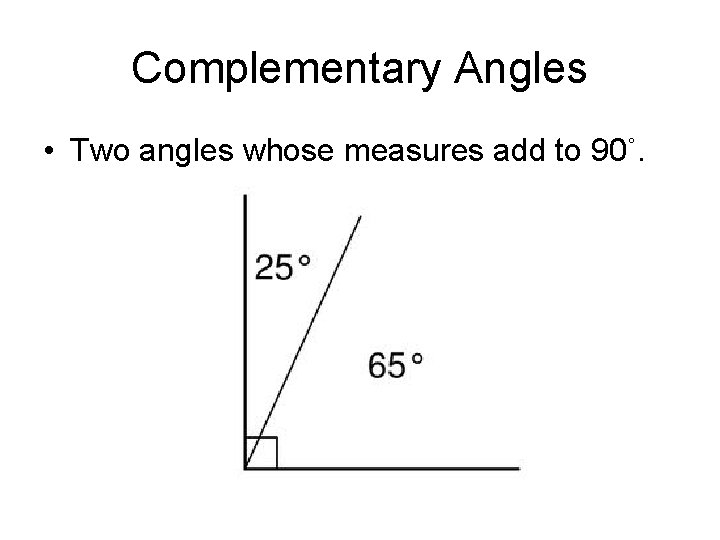
Complementary Angles • Two angles whose measures add to 90˚.

Adjacent Angles • Angles in the same plane that have a common vertex and a common side.

Angles and Parallel Lines • 1. 2. 3. • 1. 2. If two parallel lines are cut by a transversal, then the following pairs of angles are congruent. Corresponding angles Alternate interior angles Alternate exterior angles If two parallel lines are cut by a transversal, then the following pairs of angles are supplementary. Consecutive interior angles Continued…. . Consecutive exterior angles

Corresponding Angles: Two angles that occupy corresponding positions. 2 6, 1 5, 3 7, 4 8 1 3 4 5 7 2 6 8

Consecutive Angles Consecutive Interior Angles: Two angles that lie between parallel lines on the same sides of the transversal. m 3 +m 5 = 180º, m 4 +m 6 = 180º Consecutive Exterior Angles: Two angles that lie outside parallel lines on the same sides of the transversal. 1 2 m 1 +m 7 = 180º, m 2 +m 8 = 180º 3 4 5 6 7 8

Alternate Angles • Alternate Interior Angles: Two angles that lie between parallel lines on opposite sides of the transversal (but not a 3 6, 4 5 linear pair). 2 lie outside 7, 1 8 • Alternate Exterior Angles: Two angles that parallel lines on opposite sides of the transversal. 1 3 4 5 7 2 6 8

Example: If line AB is parallel to line CD and s is parallel to t, find the measure of all the angles when m< 1 = 100°. Justify your answers. A 1 4 C 5 8 m<2=80° m<3=100° m<4=80° 2 12 3 6 13 14 16 15 7 s m<5=100° m<6=80° m<7=100° m<8=80° m<9=100° m<10=80° m<11=100° m<12=80° m<13=100° m<14=80° m<15=100° m<16=80° 9 t 10 11 B D

Exampl. If line AB is parallel to line CD and s is parallel to t, find: e: 1. the value of x, if m<3 = 4 x + 6 and the m<11 = 126. 2. the value of x, if m<1 = 100 and m<8 = 2 x + 10. 3. the value of y, if m<11 = 3 y – 5 and m<16 = 2 y + 20. ANSWERS: 1. 30 A 4 C 5 8 2. 35 3. 33 1 s 2 9 12 3 6 13 14 16 15 7 t 10 11 B D