Topic 3 2 D Transformations Homogeneous coordinates Homogeneous

Topic 3: 2 D Transformations • Homogeneous coordinates • Homogeneous 2 D transformations • Affine transformations & restrictions

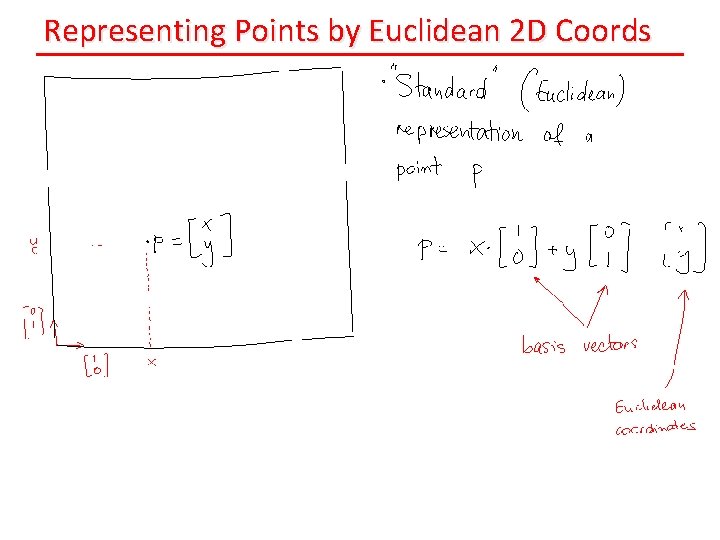
Representing Points by Euclidean 2 D Coords

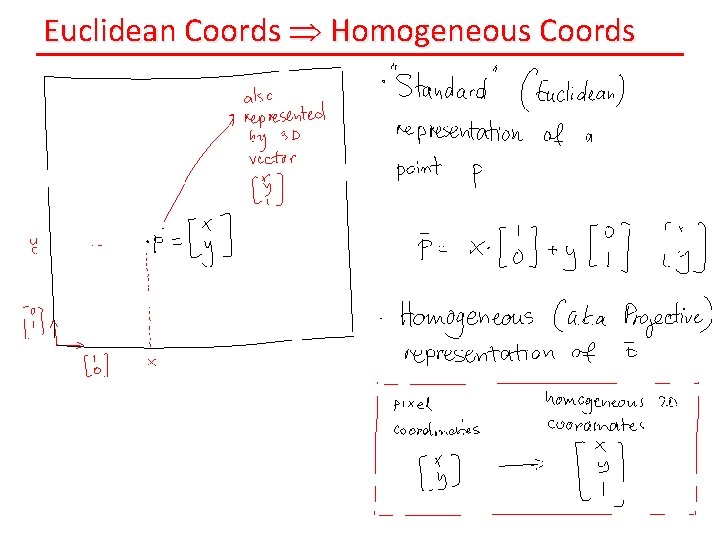
Euclidean Coords Homogeneous Coords

2 D Homogeneous Coordinates: Definition

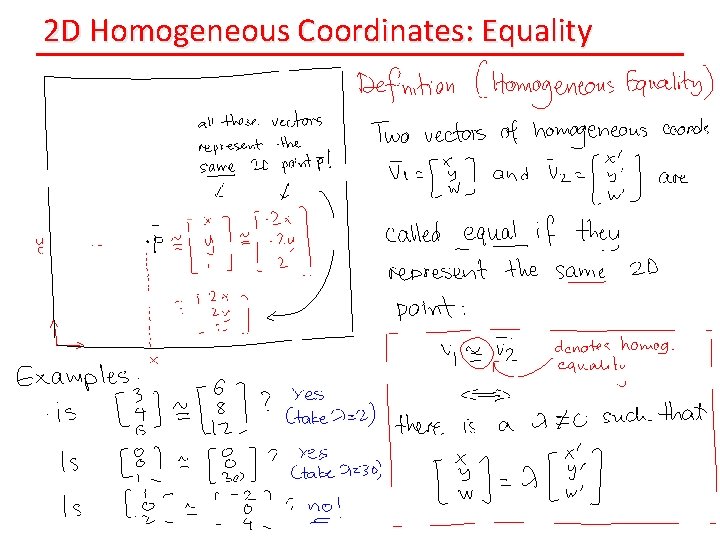
2 D Homogeneous Coordinates: Equality

Homogeneous Coords Euclidean Coords

Homogeneous Coords Euclidean Coords

Points at ∞ in Homogeneous Coordinates

Points at ∞ in Homogeneous Coordinates

Points at ∞ in Homogeneous Coordinates

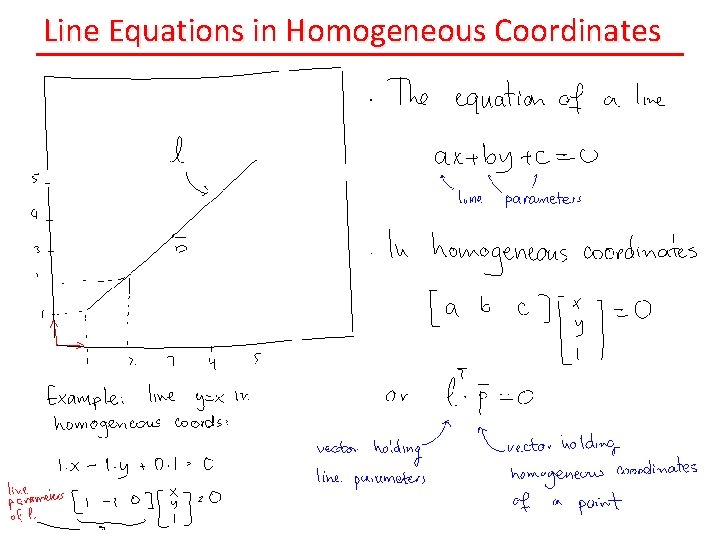
Line Equations in Homogeneous Coordinates

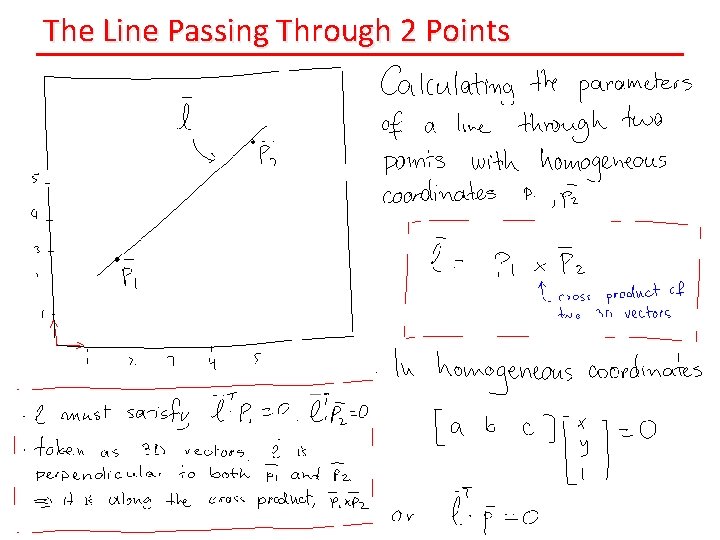
The Line Passing Through 2 Points

The Point of Intersection of Two Lines

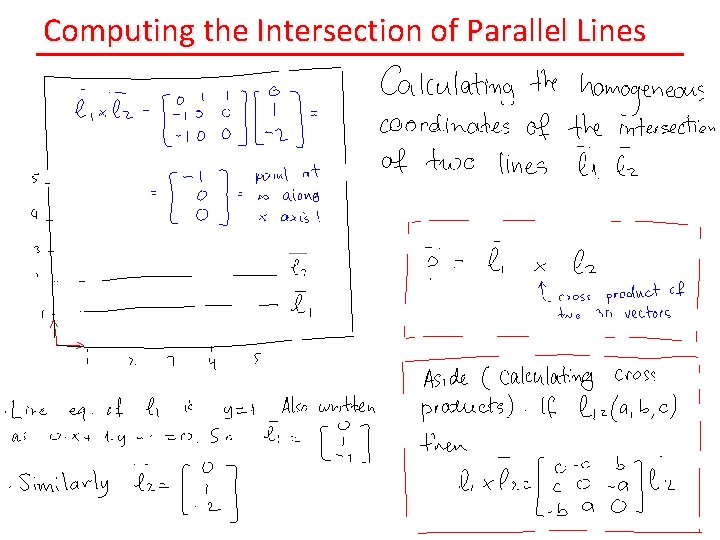
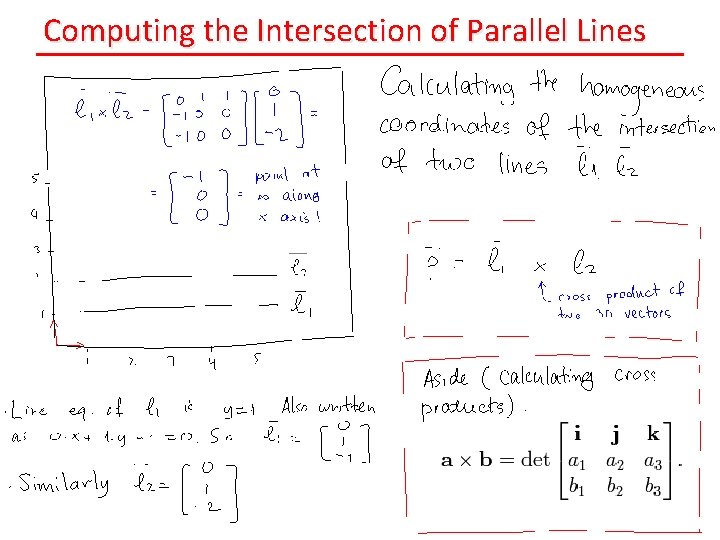
Computing the Intersection of Parallel Lines

Computing the Intersection of Parallel Lines

Computing the Intersection of Parallel Lines

Lines from Points & Points from Lines

Topic 3: 2 D Transformations • Homogeneous coordinates • Homogeneous 2 D transformations • Affine transformations & restrictions

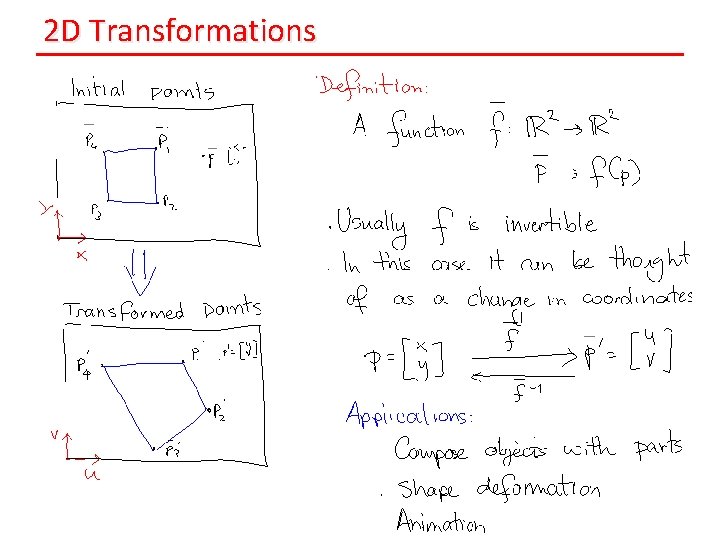
2 D Transformations

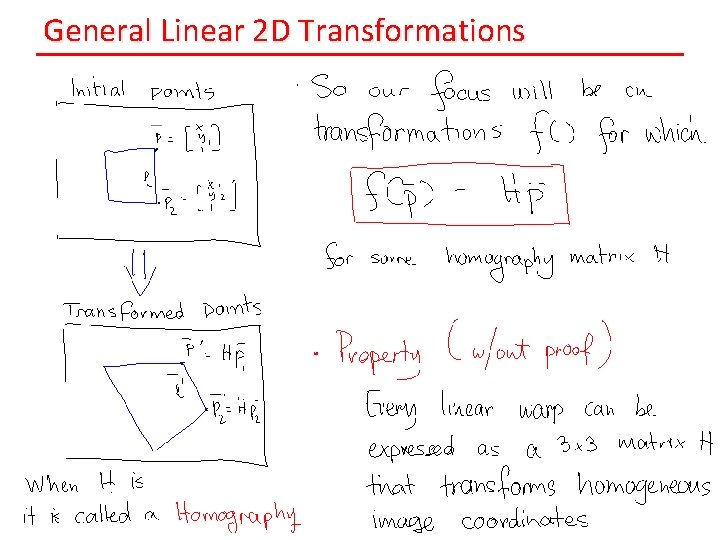
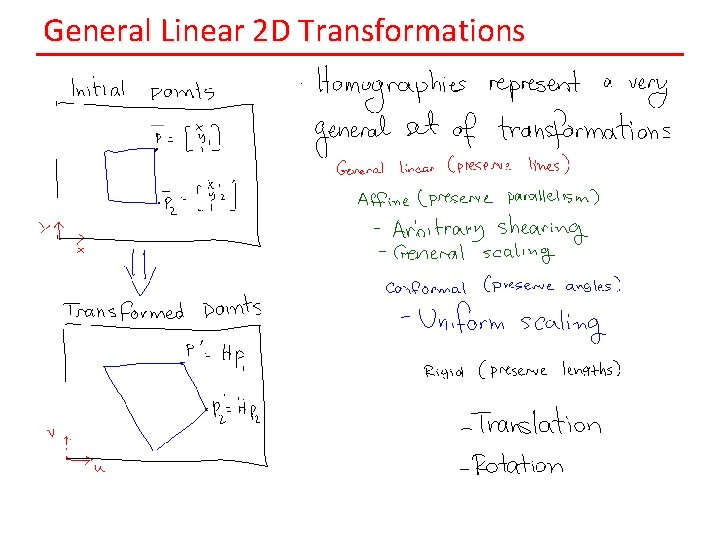
General Linear 2 D Transformations

General Linear 2 D Transformations

Homographies: Basic properties

Homographies: Basic properties Why can’t we just multiply H into the line equation?

Homographies: Basic properties

Homographies: Basic properties

Homographies: Basic properties

Homographies: Basic properties

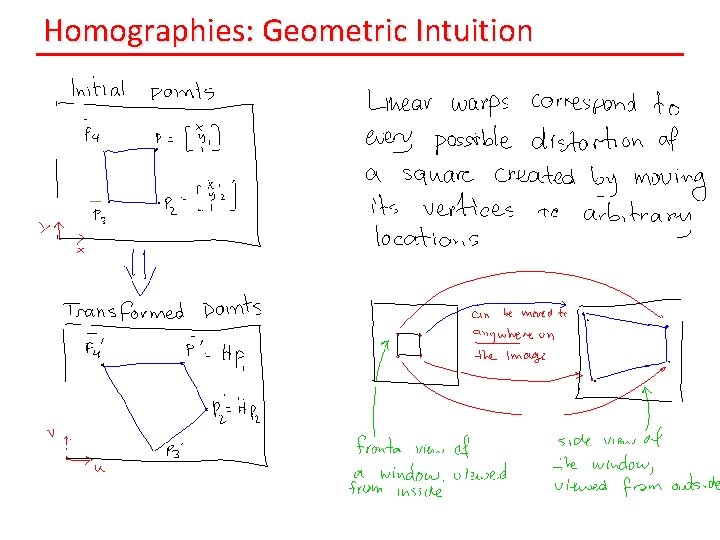
Homographies: Geometric Intuition

Homographies from Point Correspondences

Homographies from Point Correspondences

Homographies from Point Correspondences

Topic 3: 2 D Transformations • Homogeneous coordinates • Homogeneous 2 D transformations • Affine transformations & restrictions

General Linear 2 D Transformations

Affine Transformations

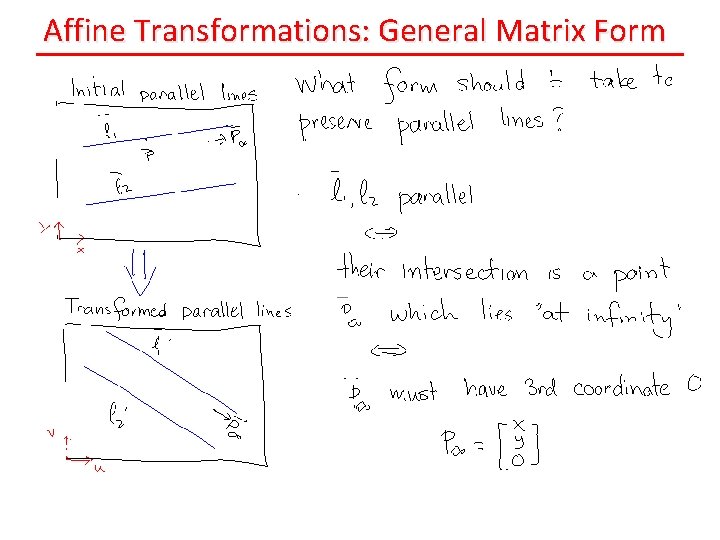
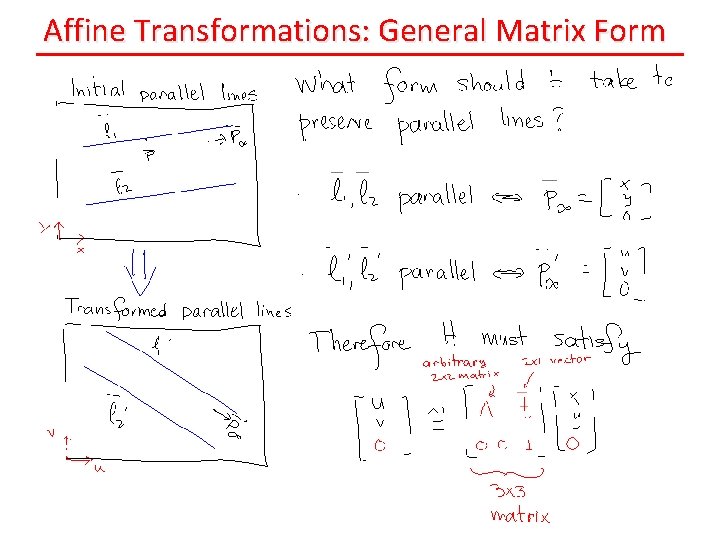
Affine Transformations: General Matrix Form

Affine Transformations: General Matrix Form

Affine Transformations: Basic Properties

Affine Transformations: Basic Properties

Affine Transformations: Basic Properties

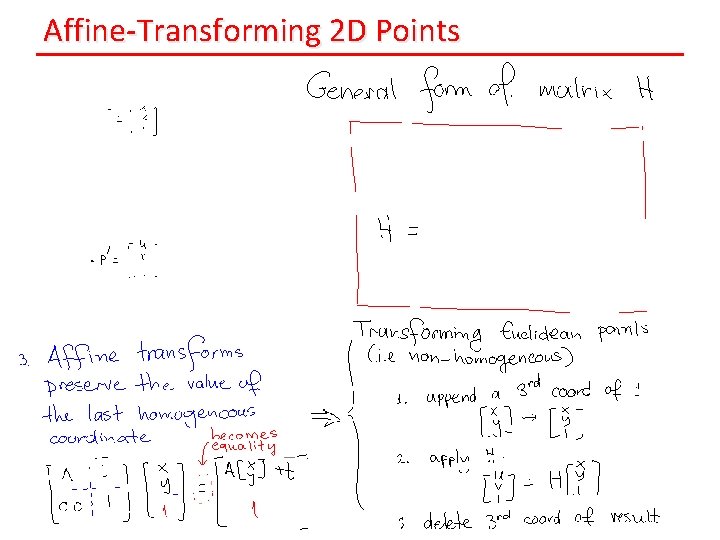
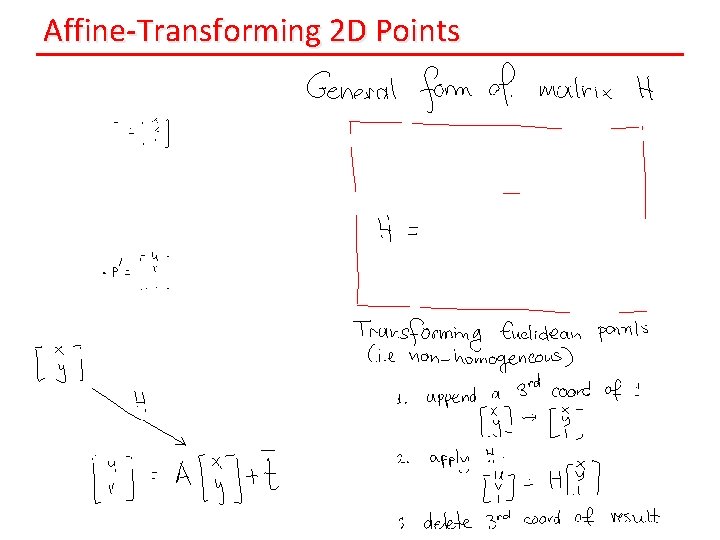
Affine-Transforming 2 D Points

Affine-Transforming 2 D Points

Affine-Transforming 2 D Points

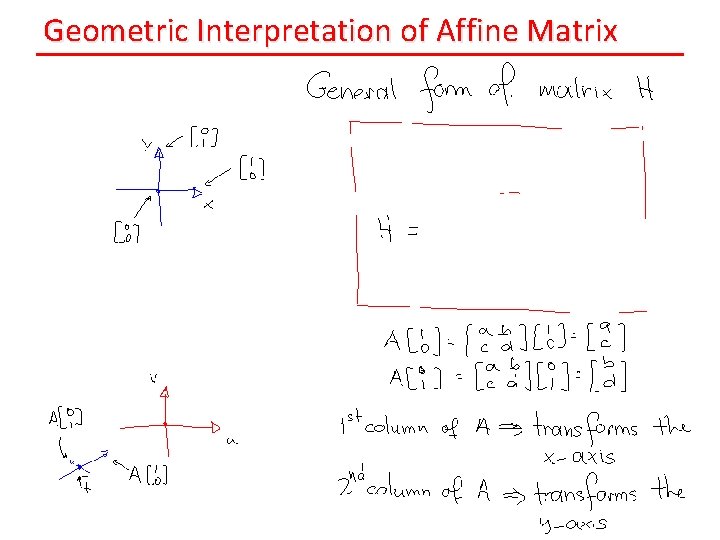
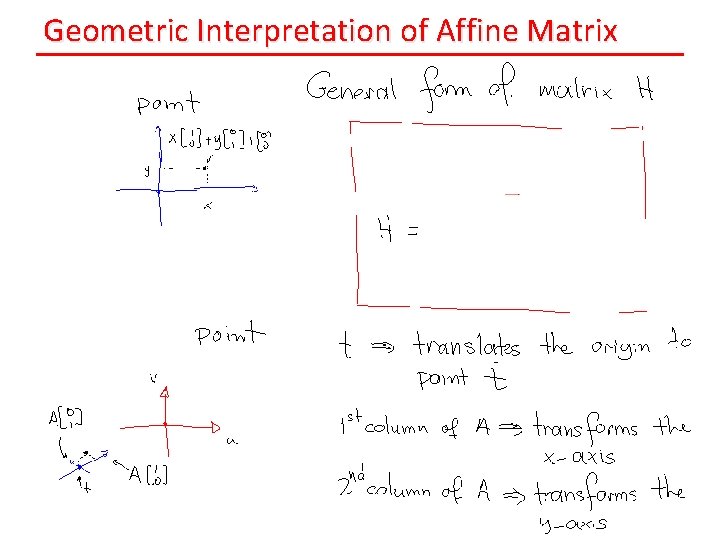
Geometric Interpretation of Affine Matrix

Geometric Interpretation of Affine Matrix

Geometric Interpretation of Affine Matrix

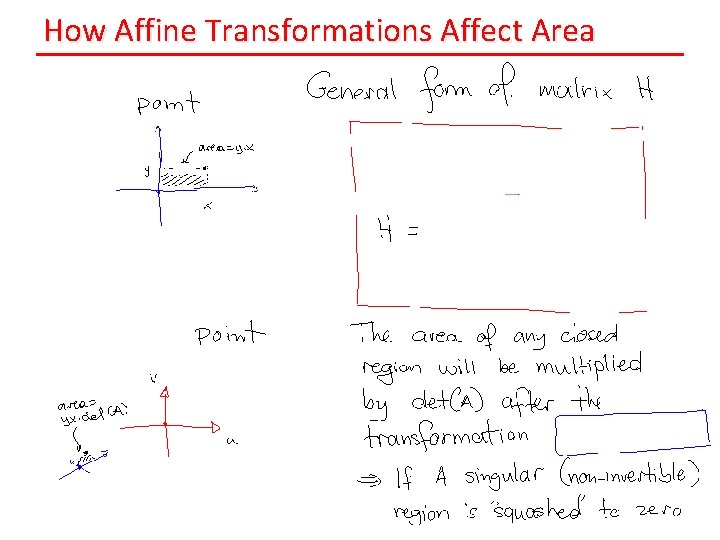
How Affine Transformations Affect Area

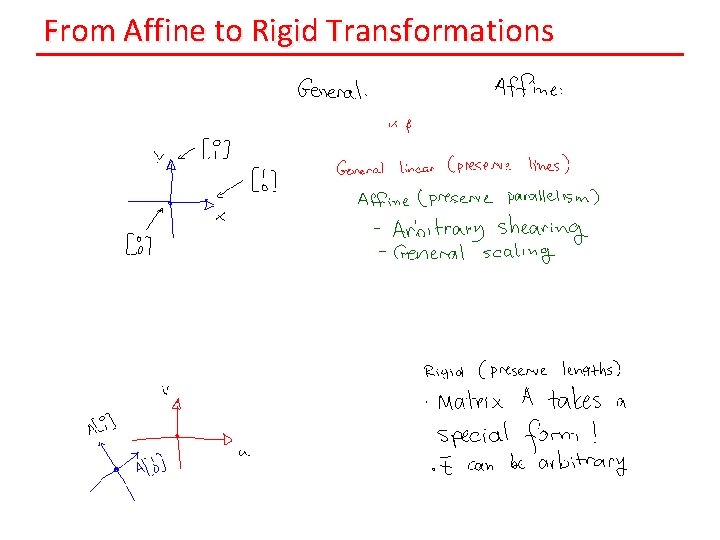
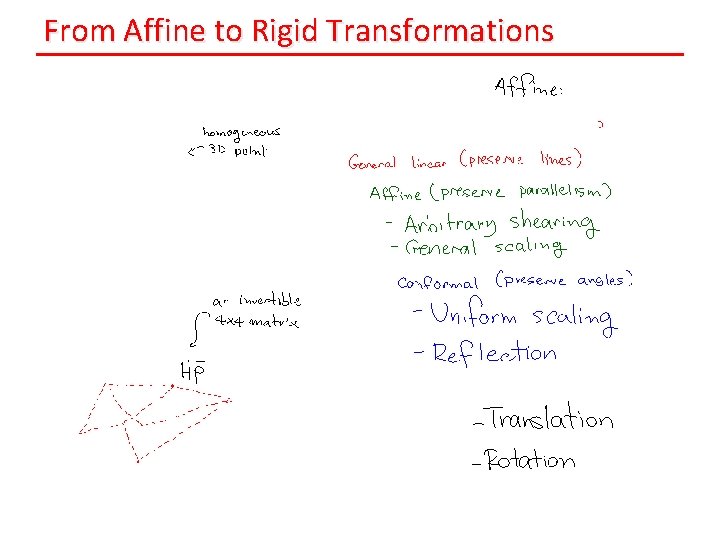
From Affine to Rigid Transformations

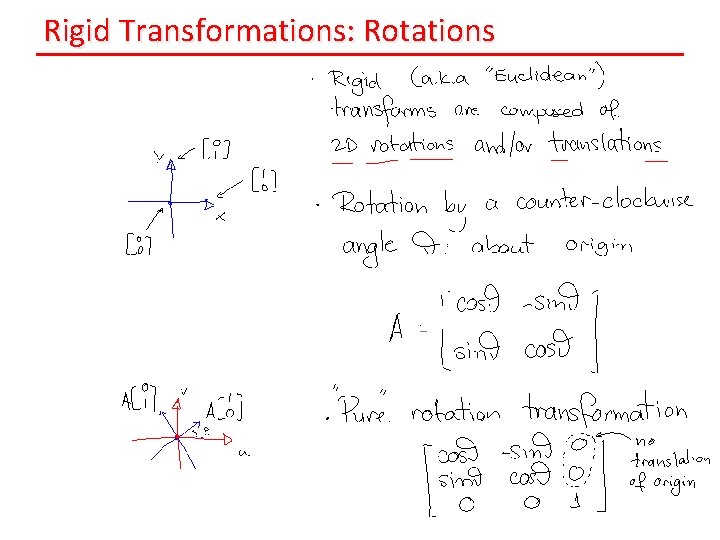
Rigid Transformations: Rotations

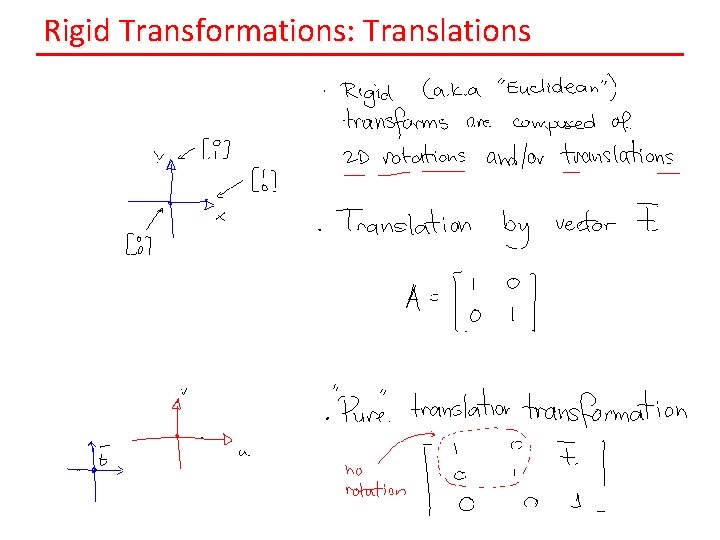
Rigid Transformations: Translations

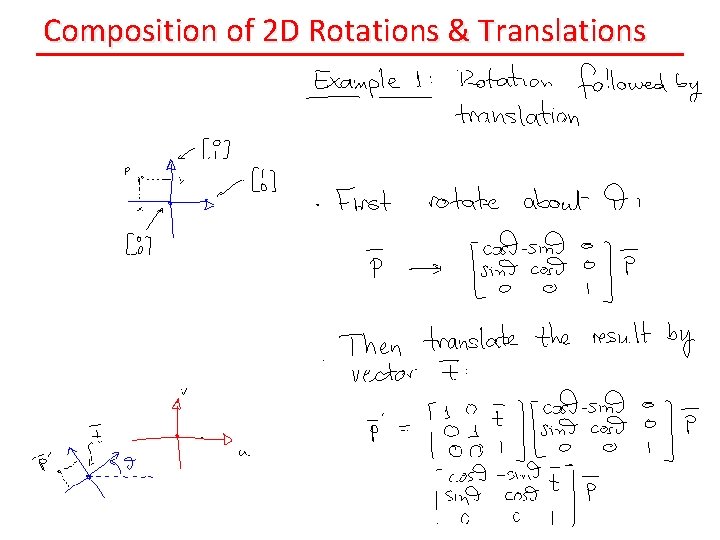
Composition of 2 D Rotations & Translations

Composition of 2 D Translations & Rotations

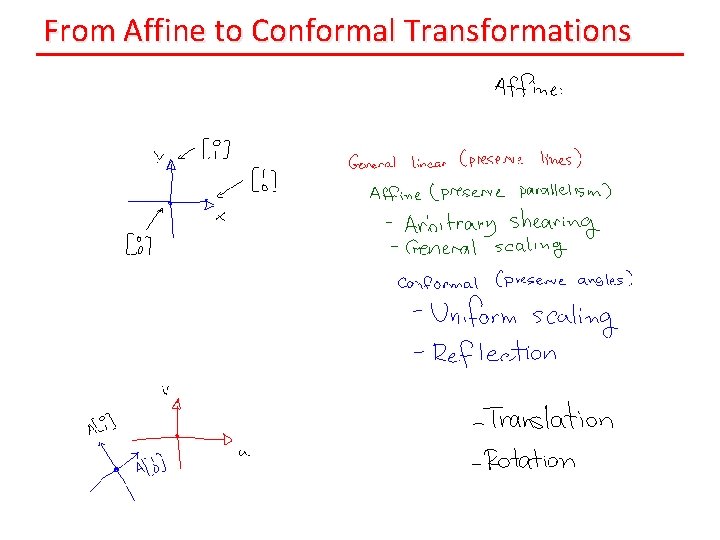
From Affine to Conformal Transformations

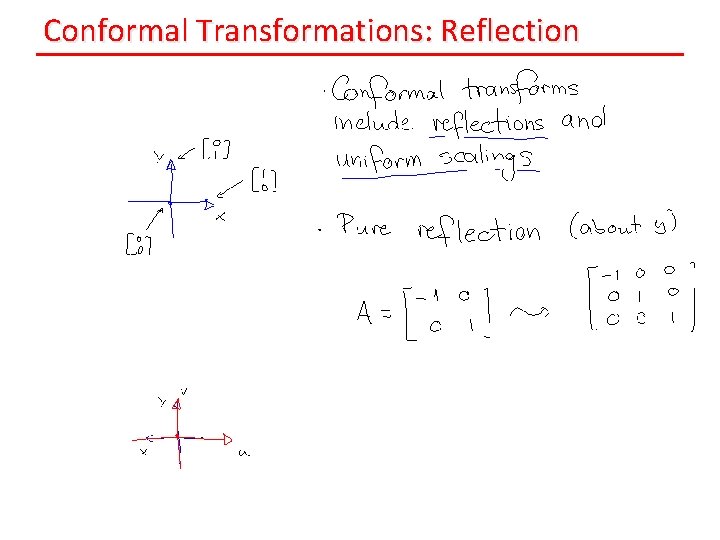
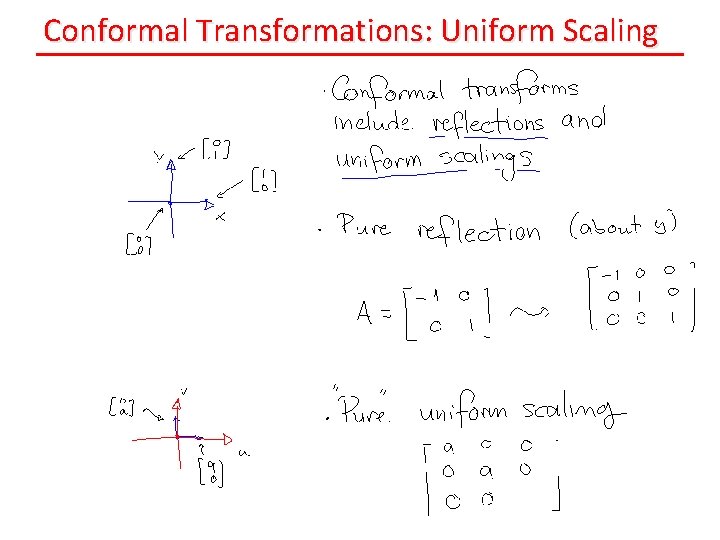
Conformal Transformations: Reflection

Conformal Transformations: Uniform Scaling

Topic 4: Coordinate-Free Geometry (CFG) • A brief introduction & basic ideas

Doing Geometry Without Coordinates

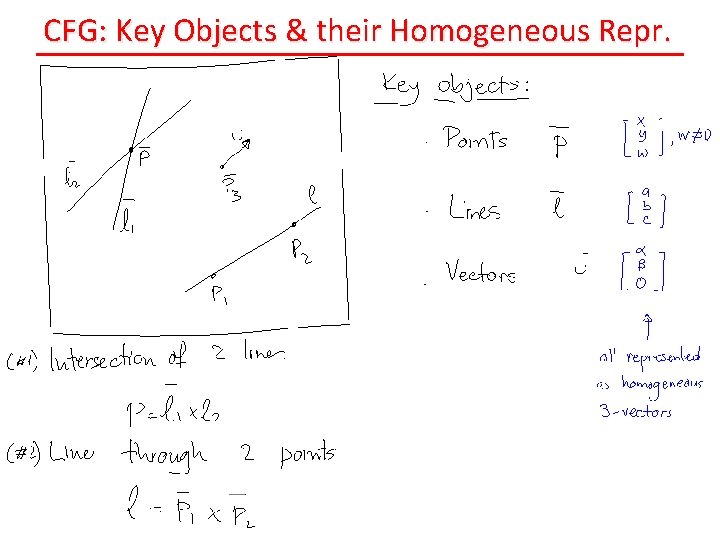
CFG: Key Objects & their Homogeneous Repr.

CFG: Basic Geometric Operations

CFG: “Legal” vs. “Undefined” Geometric Ops

More CFG Ops: Linear Vector Combination

More CFG Ops: Affine Point Combination

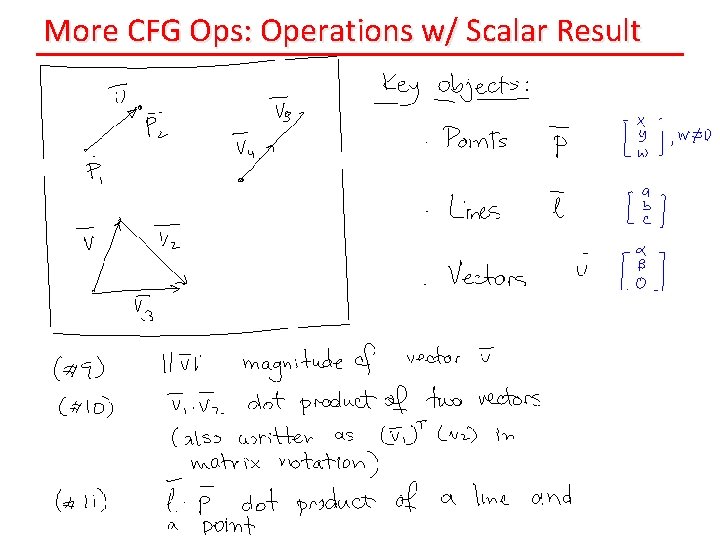
More CFG Ops: Operations w/ Scalar Result

Topic 5: 3 D Objects • • General curves & surfaces in 3 D Normal vectors, surface curves & tangent planes Implicit surface representations Example surfaces: surfaces of revolution, bilinear patches, quadrics

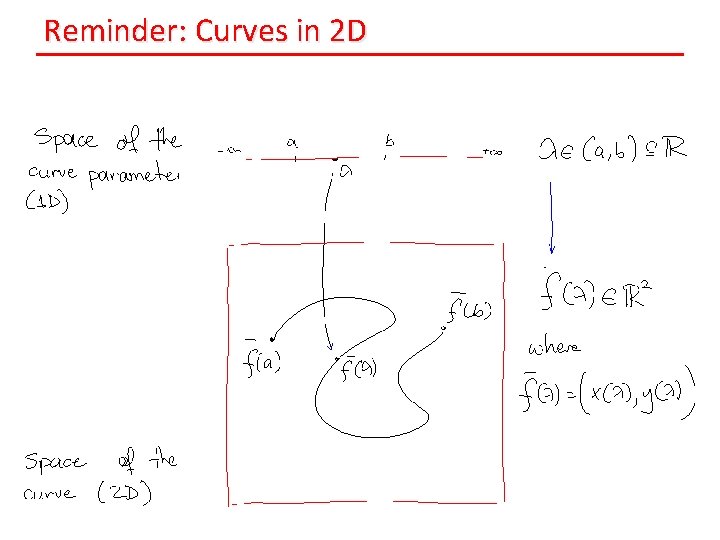
Reminder: Curves in 2 D

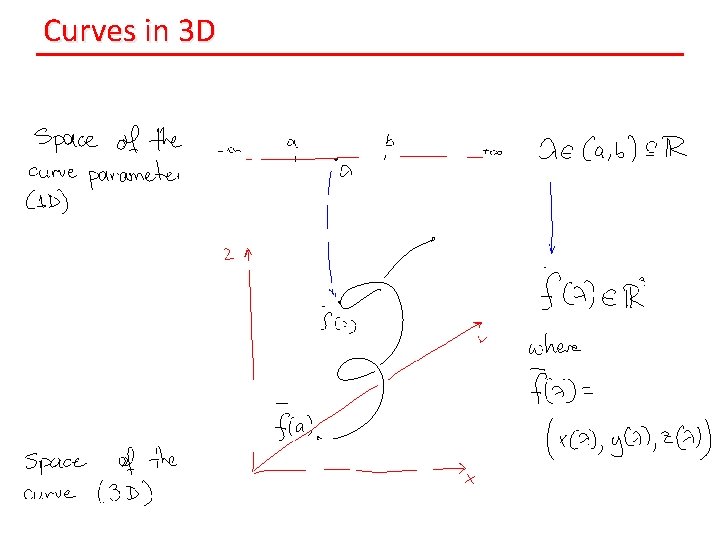
Curves in 3 D

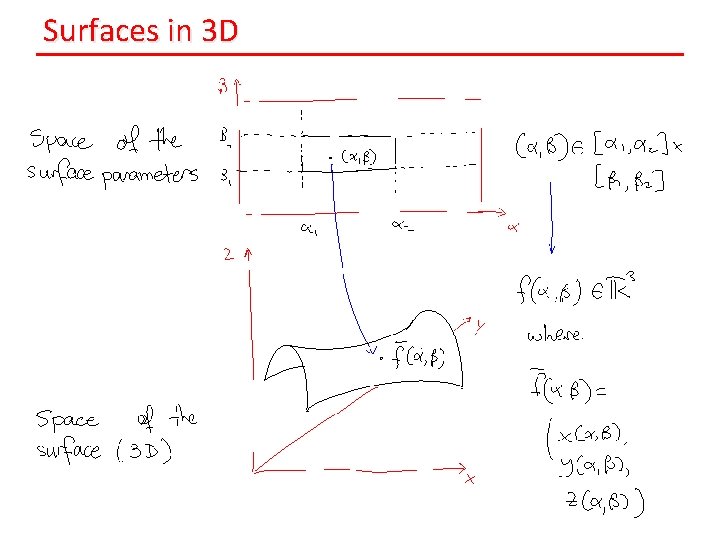
Surfaces in 3 D

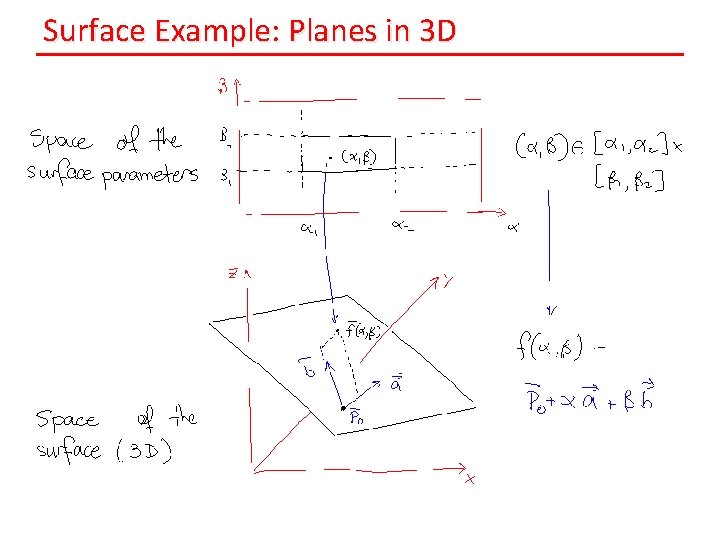
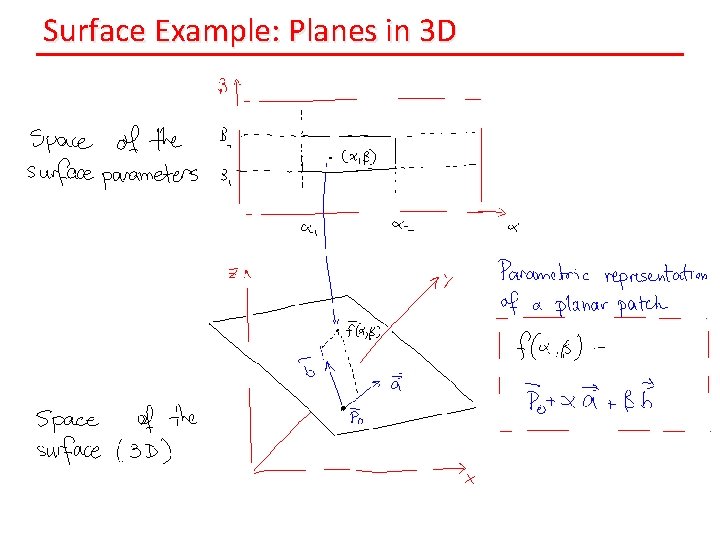
Surface Example: Planes in 3 D

Surface Example: Planes in 3 D

Topic 5: 3 D Objects • • General curves & surfaces in 3 D Normal vectors, surface curves & tangent planes Implicit surface representations Example surfaces: surfaces of revolution, bilinear patches, quadrics

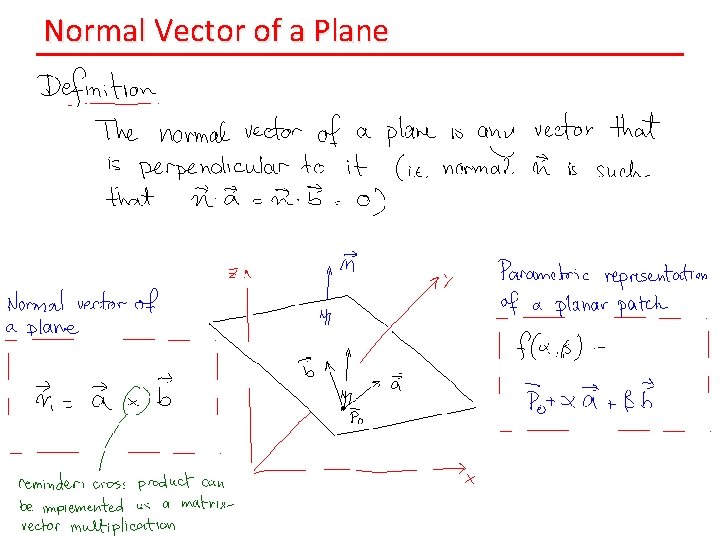
Normal Vector of a Plane

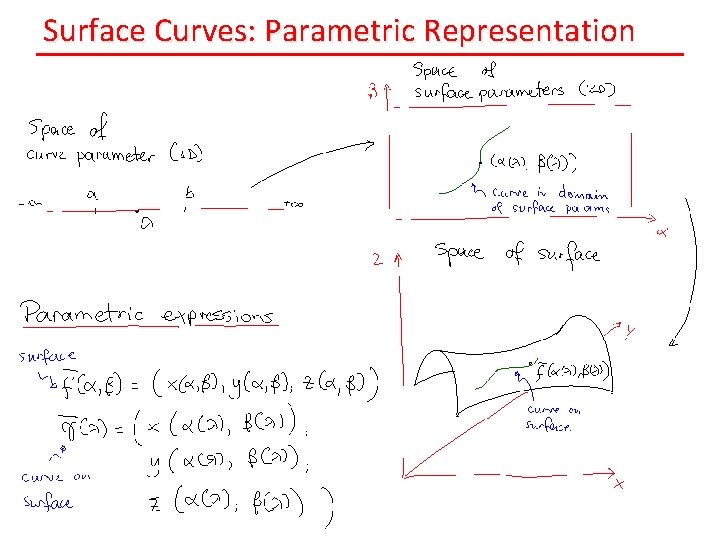
Surface Curves: Parametric Representation

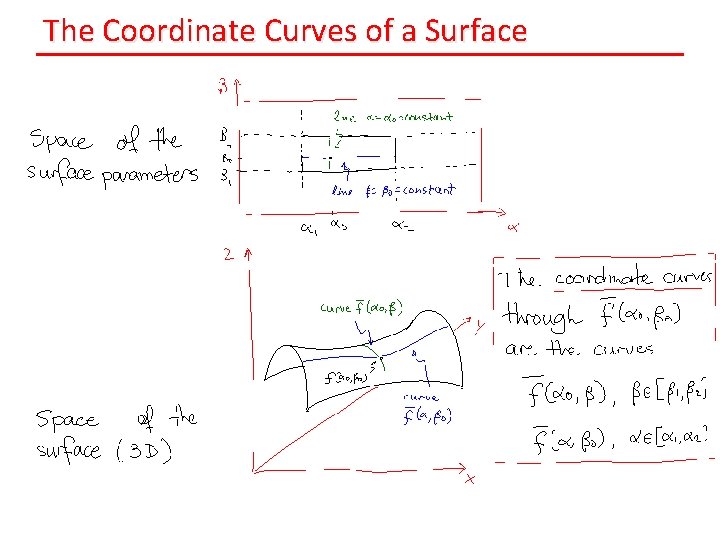
The Coordinate Curves of a Surface

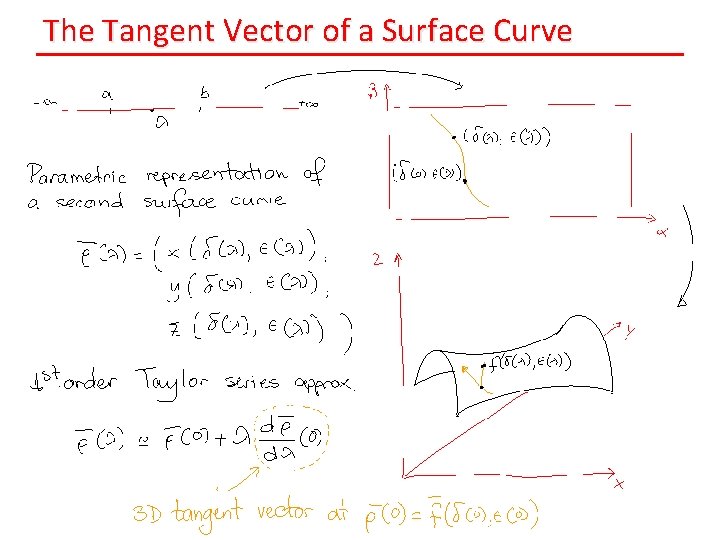
The Tangent Vector of a Surface Curve

The Tangent Vector of a Surface Curve

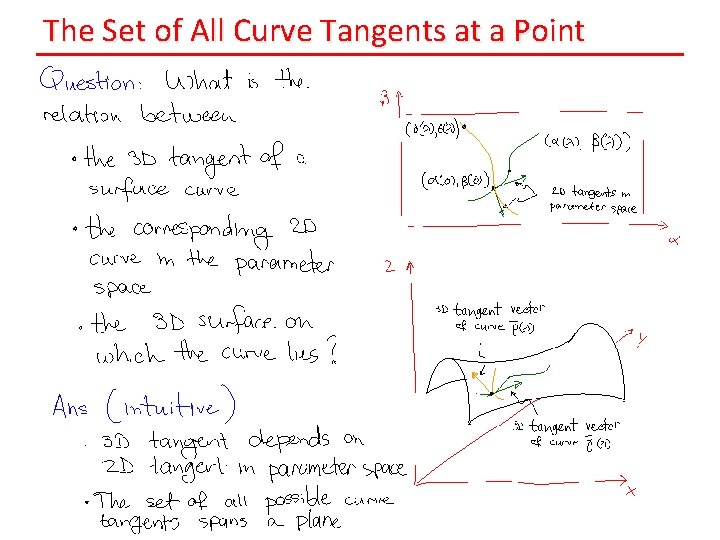
The Set of All Curve Tangents at a Point

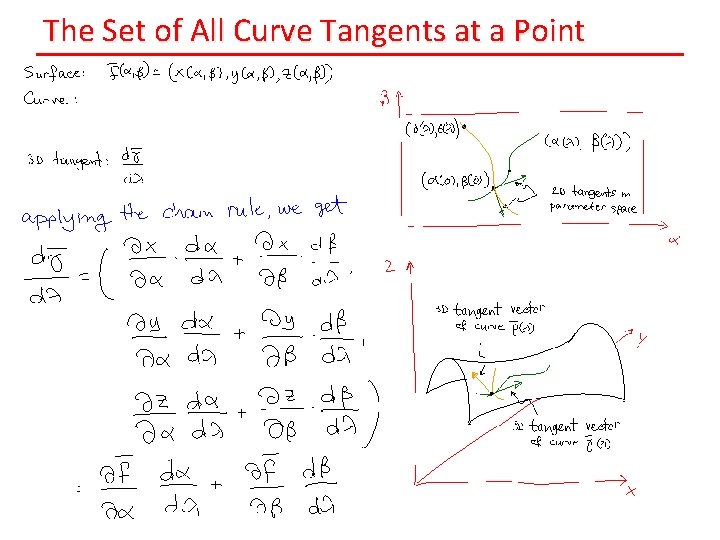
The Set of All Curve Tangents at a Point

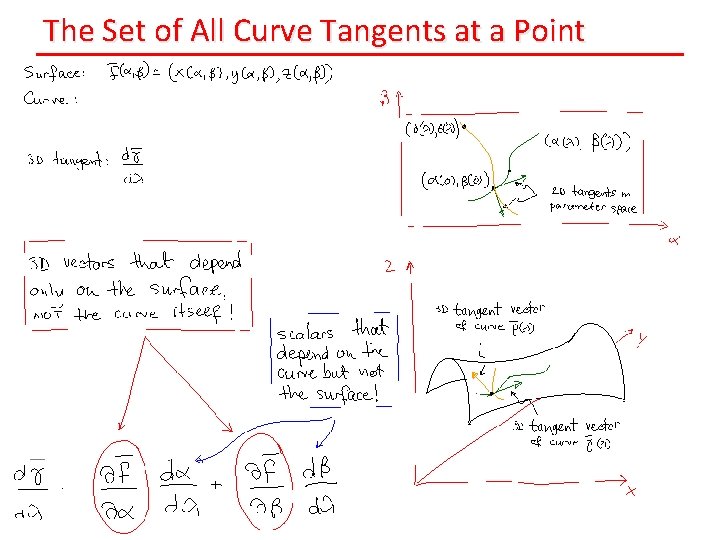
The Set of All Curve Tangents at a Point

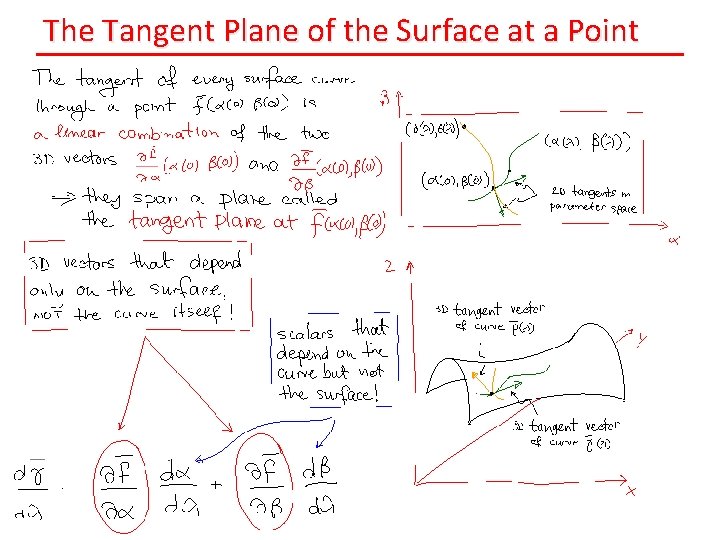
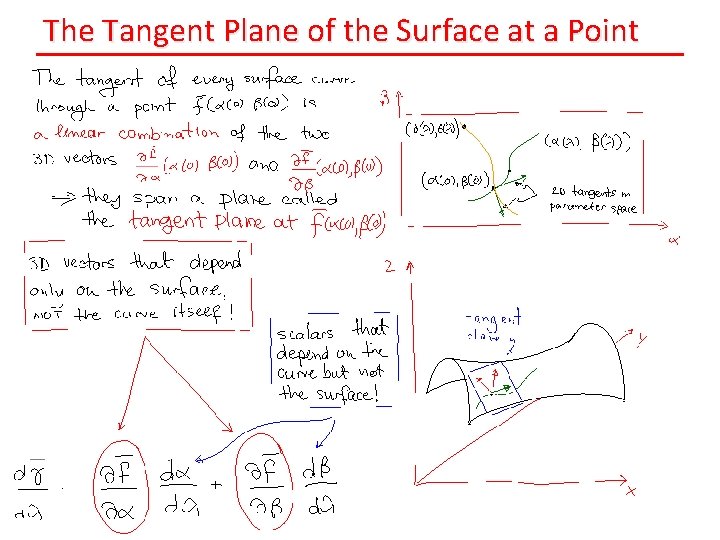
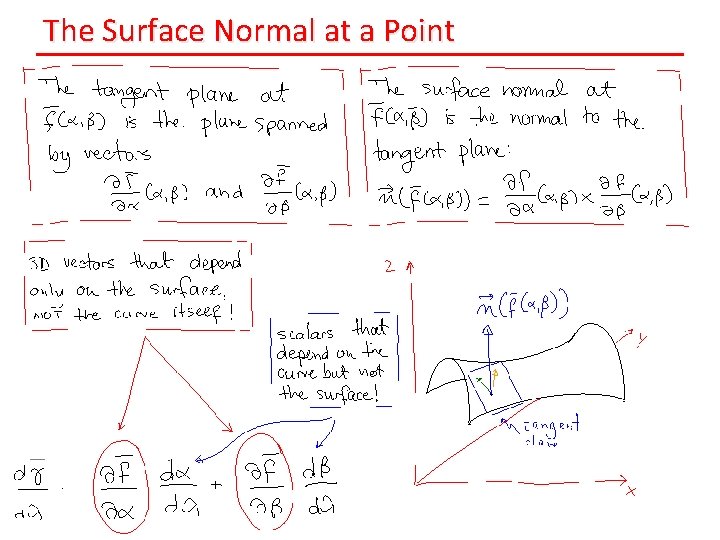
The Tangent Plane of the Surface at a Point

The Tangent Plane of the Surface at a Point

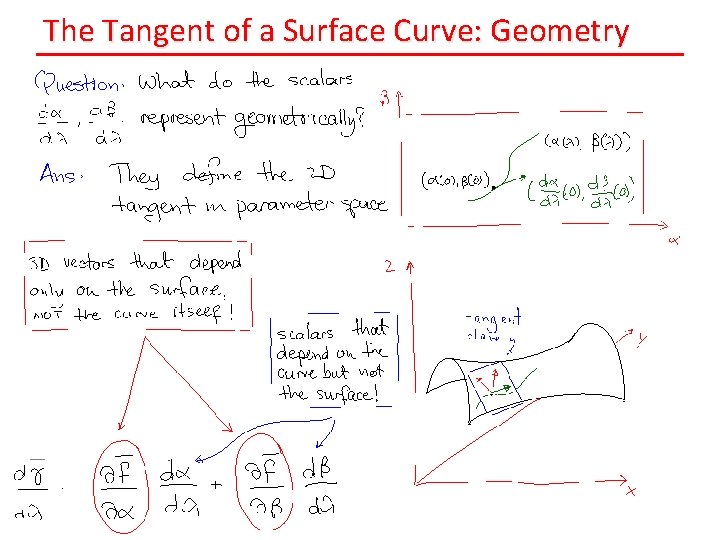
The Tangent of a Surface Curve: Geometry

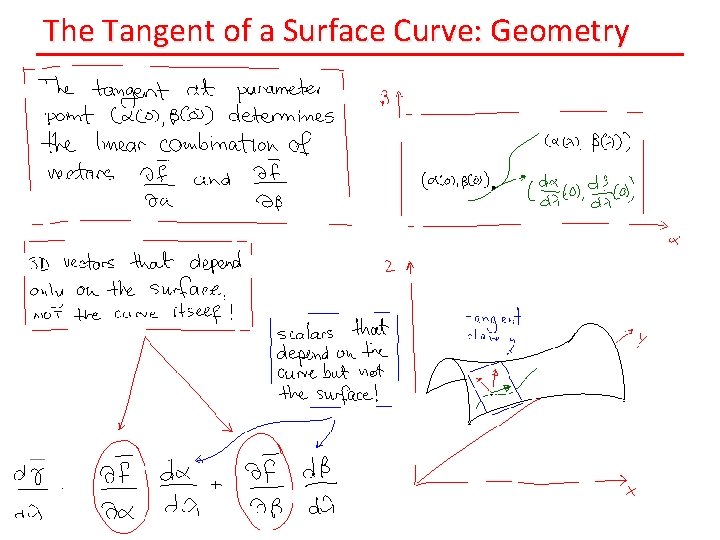
The Tangent of a Surface Curve: Geometry

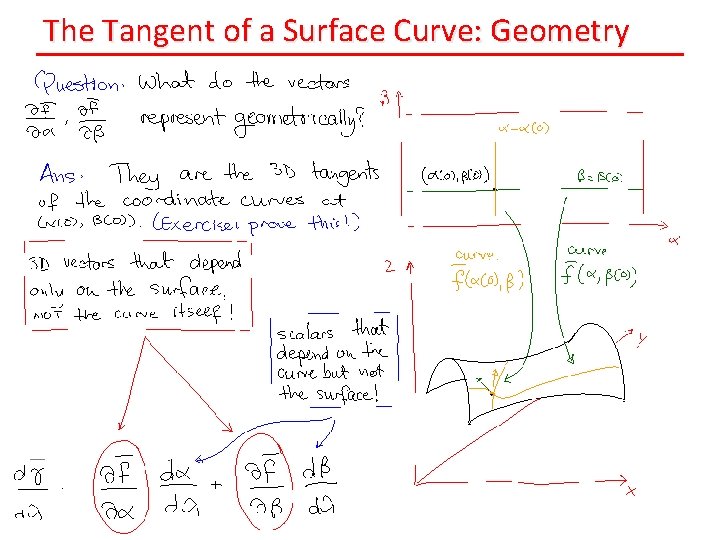
The Tangent of a Surface Curve: Geometry

The Surface Normal at a Point

Topic 5: 3 D Objects • • General curves & surfaces in 3 D Normal vectors, surface curves & tangent planes Implicit surface representations Example surfaces: surfaces of revolution, bilinear patches, quadrics

Representing Surfaces by an Implicit Function

Example: The Implicit Function of a Plane

The Level Sets of an Implicit Function

Surface Normals from the Implicit Function

Surface Normals from the Implicit Function

Surface Normals from the Implicit Function

Topic 5: 3 D Objects • • General curves & surfaces in 3 D Normal vectors, surface curves & tangent planes Implicit surface representations Example surfaces: surfaces of revolution, bilinear patches, quadrics

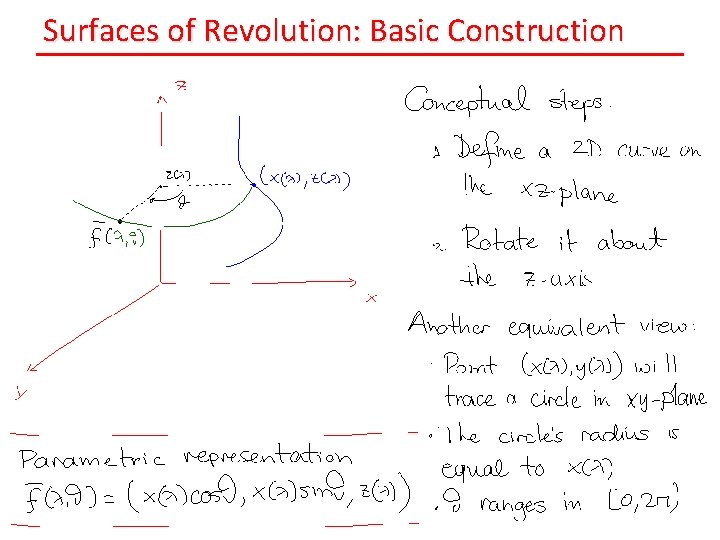
Surfaces of Revolution: Basic Construction

Example: The Cylinder

Example: Implicit Function of the Cylinder

Example: The Torus as a Surface of Revolution

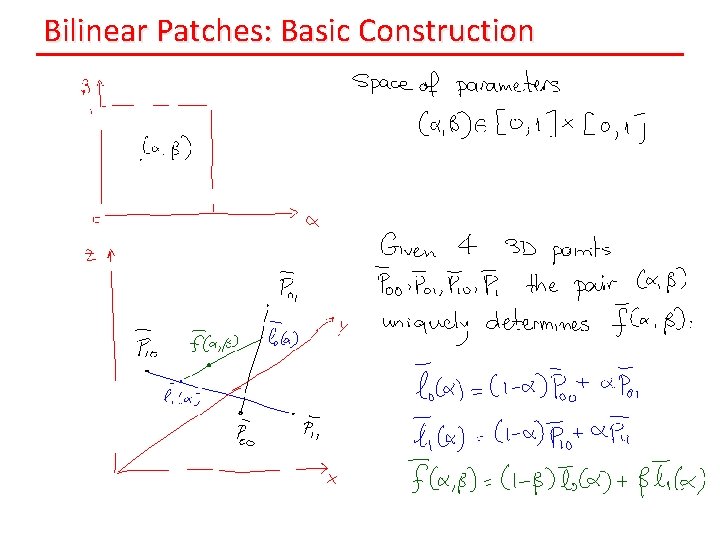
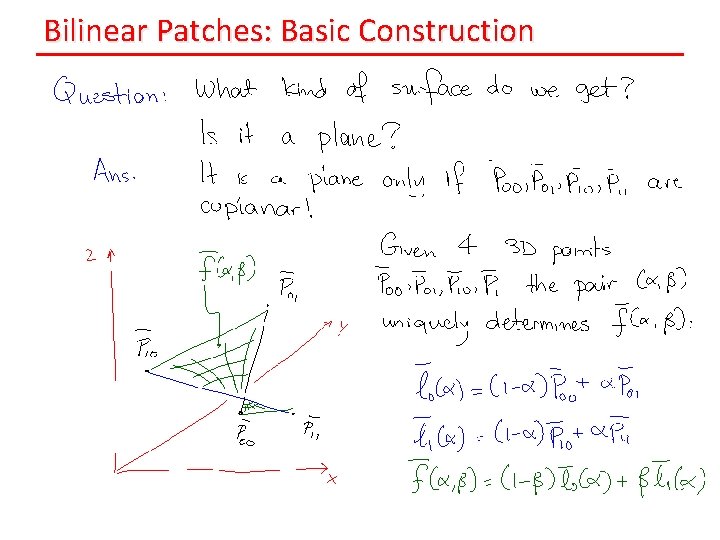
Bilinear Patches: Basic Construction

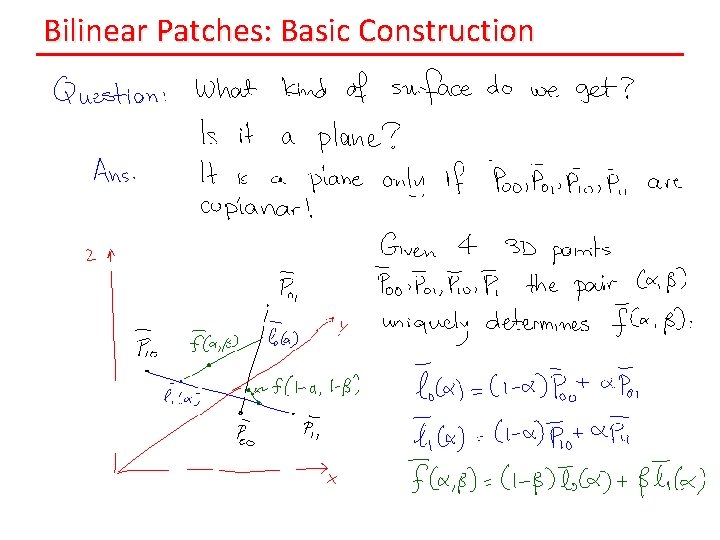
Bilinear Patches: Basic Construction

Bilinear Patches: Basic Construction

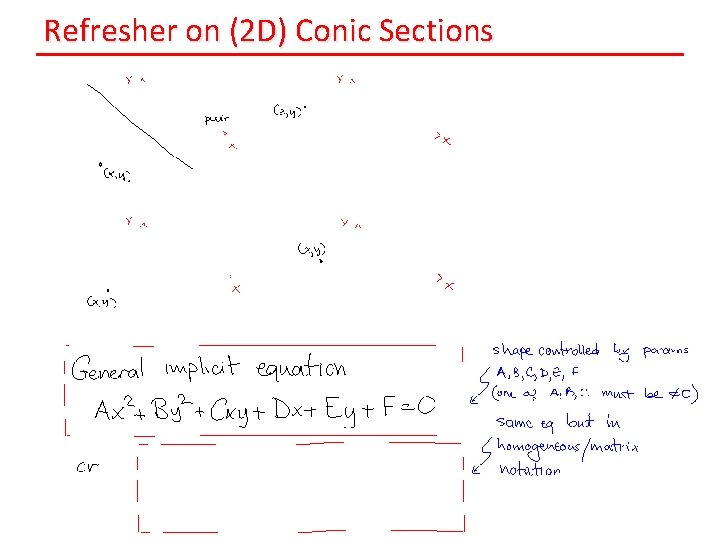
Refresher on (2 D) Conic Sections

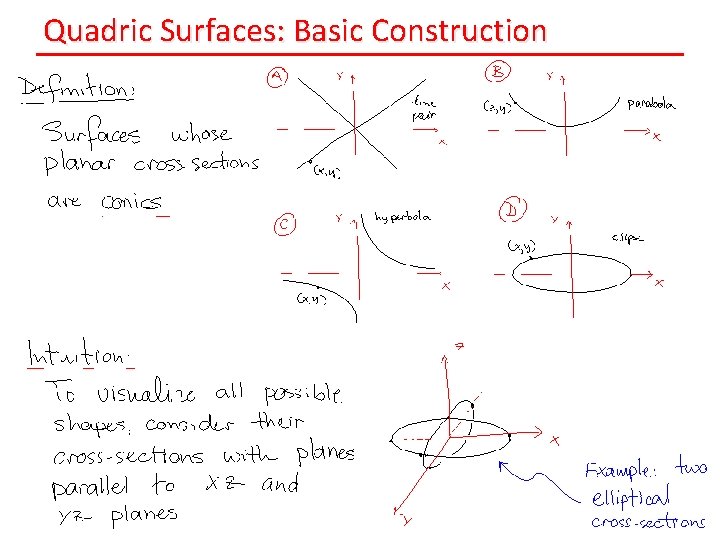
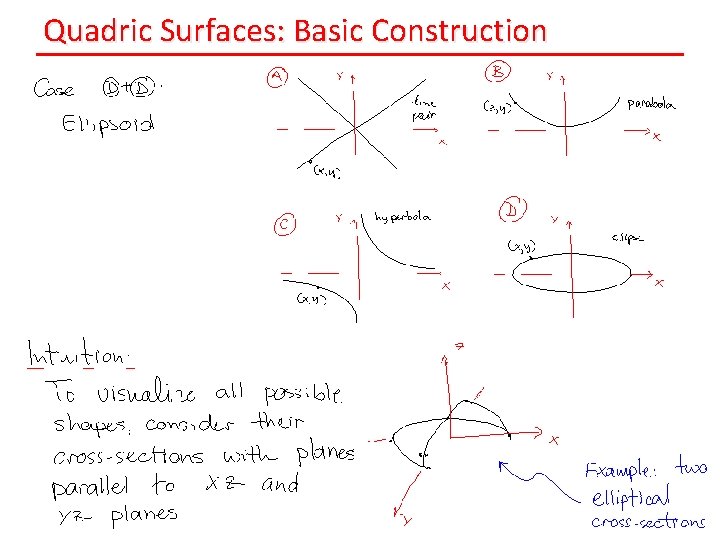
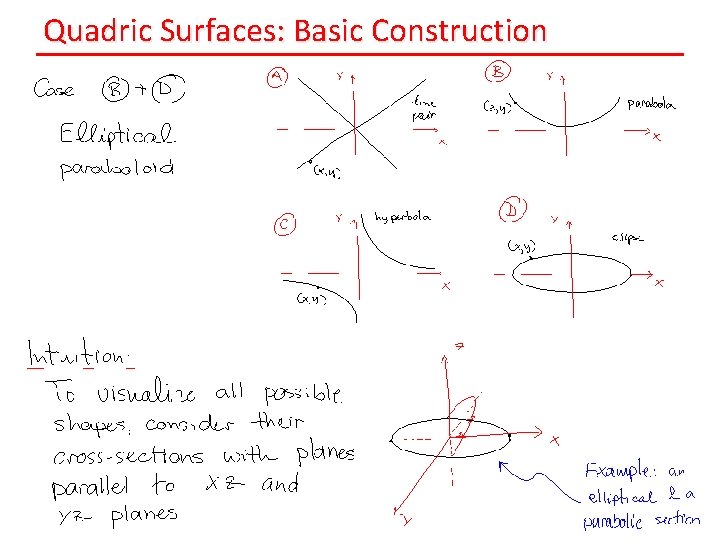
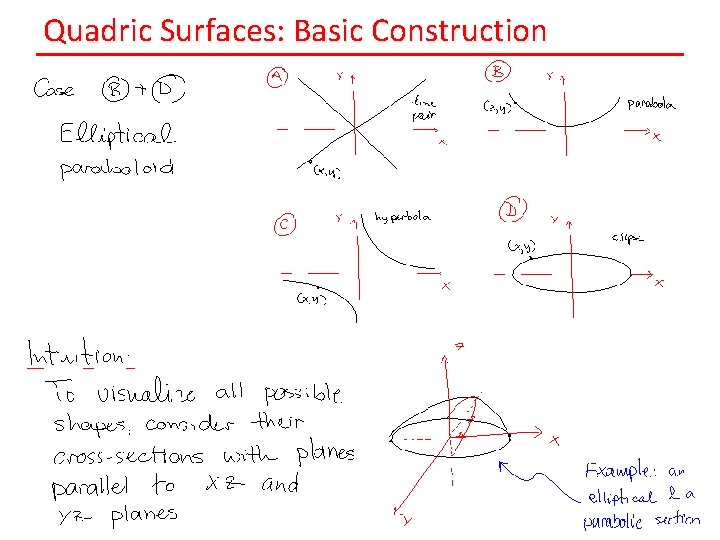
Quadric Surfaces: Basic Construction

Quadric Surfaces: Basic Construction

Quadric Surfaces: Basic Construction

Quadric Surfaces: Basic Construction

Quadric Surfaces: Basic Construction

Quadric Surfaces: Implicit Equation

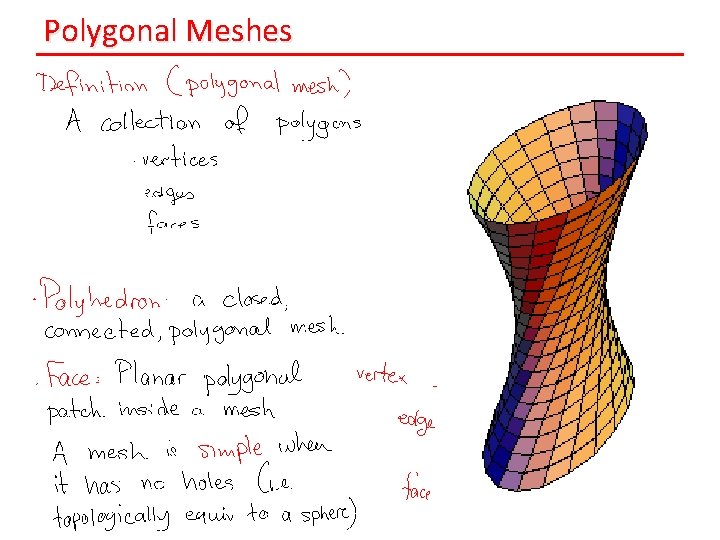
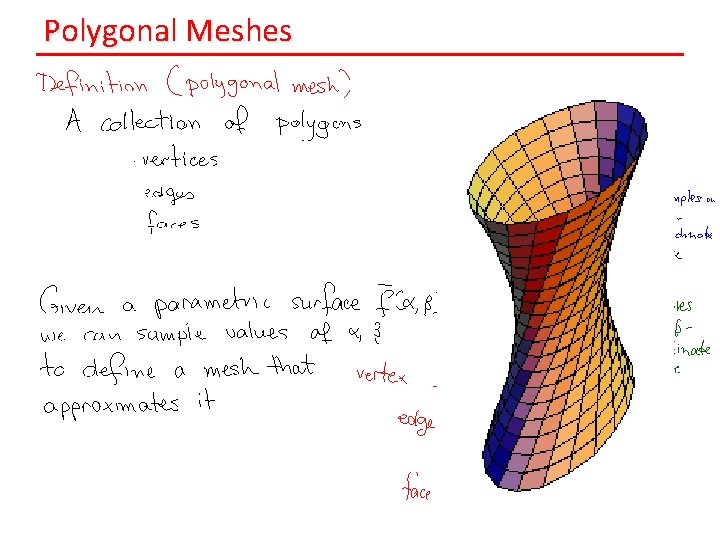
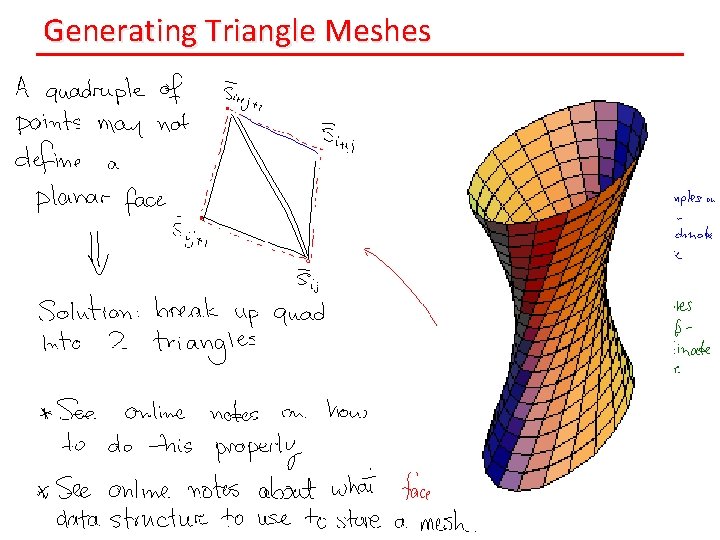
Polygonal Meshes

Polygonal Meshes

Generating Triangle Meshes

Topic 6: 3 D Transformations • Homogeneous coordinates in 3 D • Homogeneous 3 D transformations • Affine transformations & rotations in 3 D

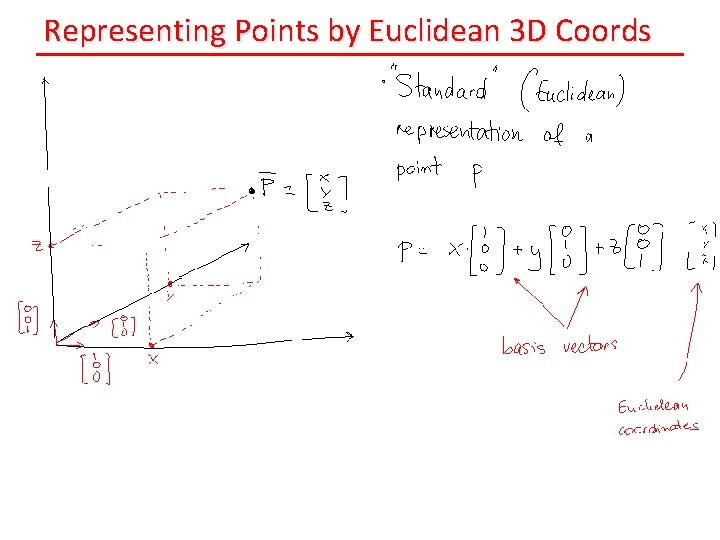
Representing Points by Euclidean 3 D Coords

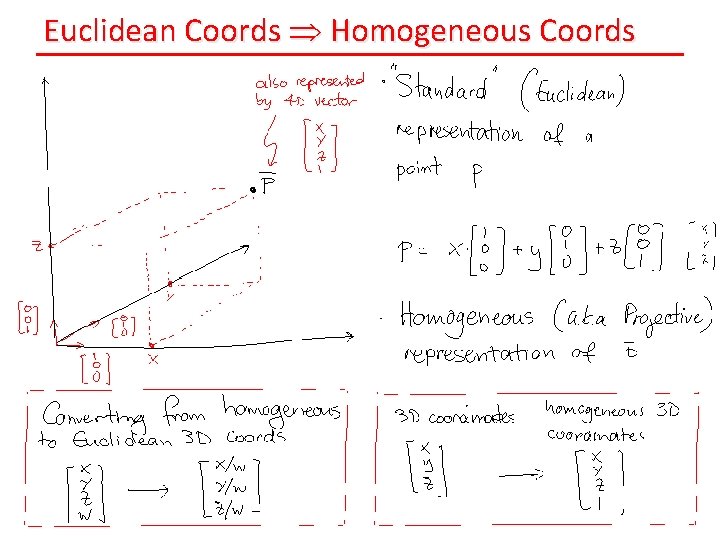
Euclidean Coords Homogeneous Coords

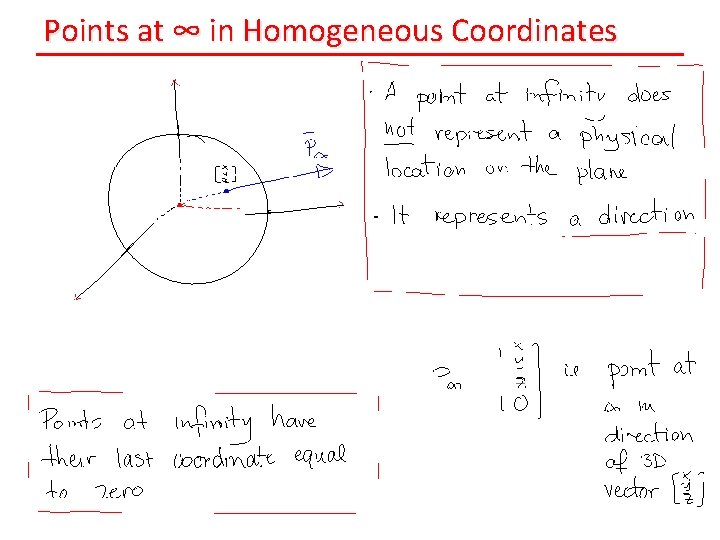
Points at ∞ in Homogeneous Coordinates

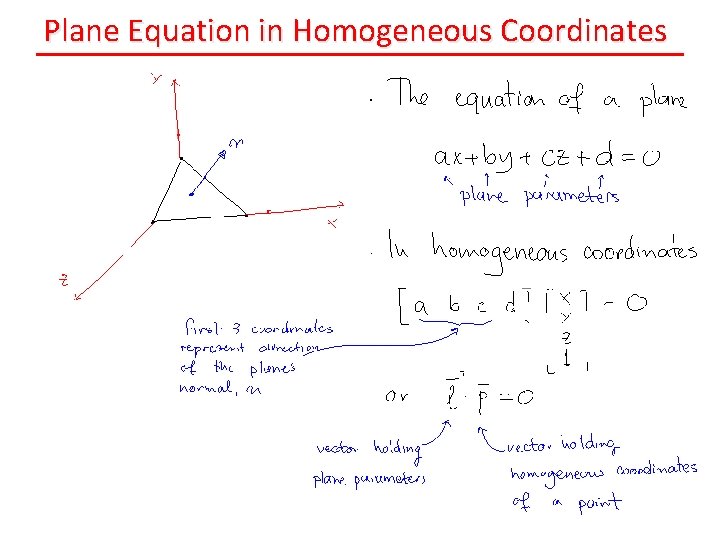
Plane Equation in Homogeneous Coordinates

Topic 6: 3 D Transformations • Homogeneous coordinates in 3 D • Homogeneous 3 D transformations • Affine transformations & rotations in 3 D

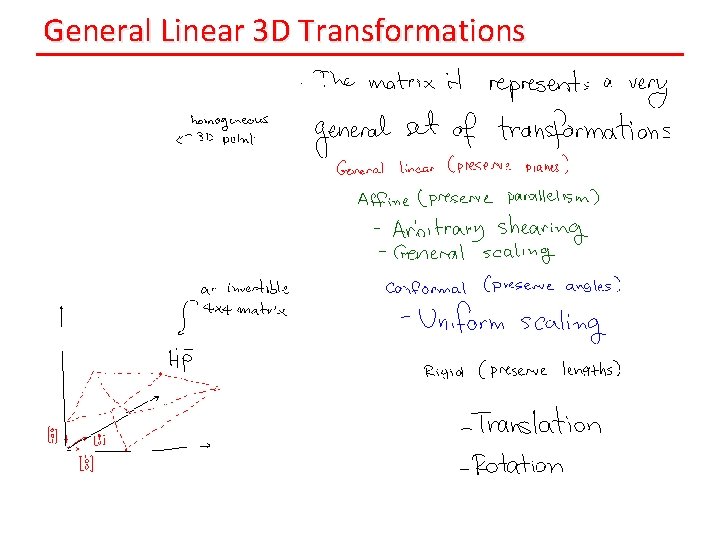
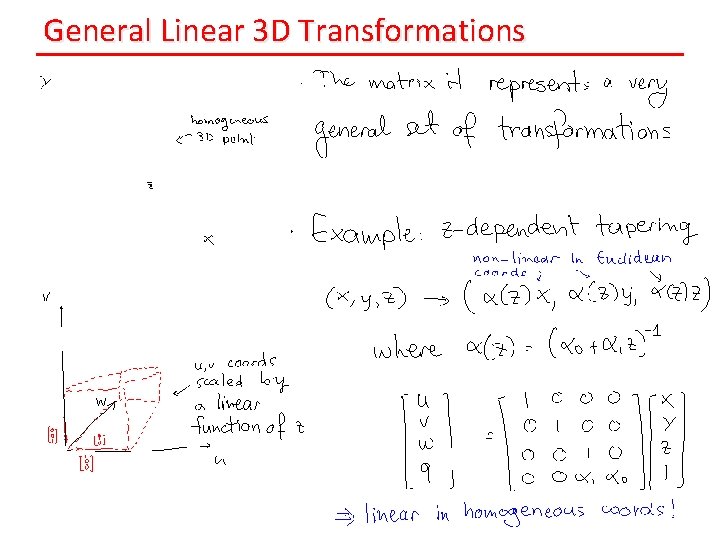
General Linear 3 D Transformations

General Linear 3 D Transformations

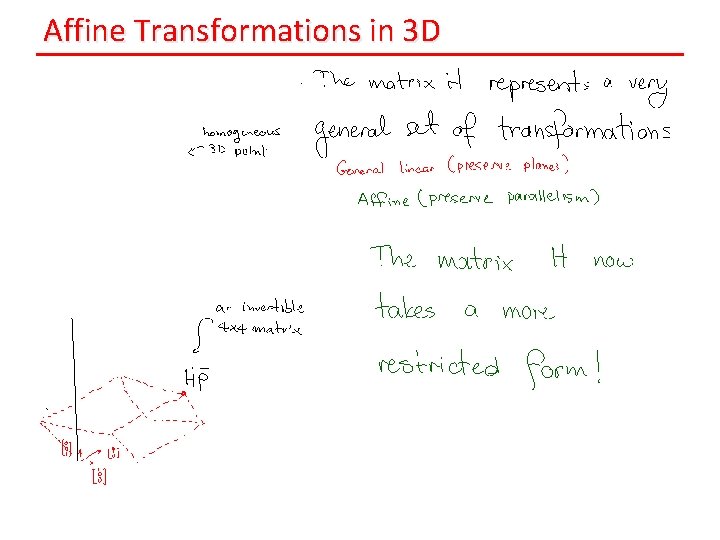
Affine Transformations in 3 D

Affine Transformations: Basic Properties

From Affine to Rigid Transformations

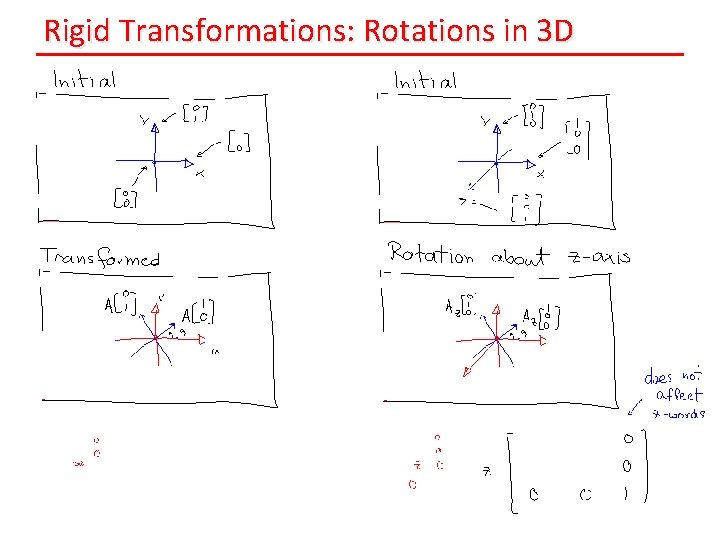
Rigid Transformations: Rotations in 3 D

Elementary Rotations in 3 D

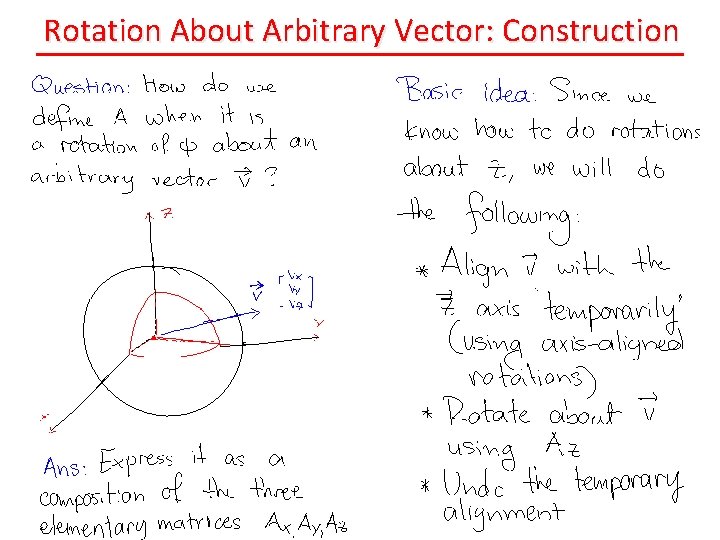
Rotation About Arbitrary Vector?

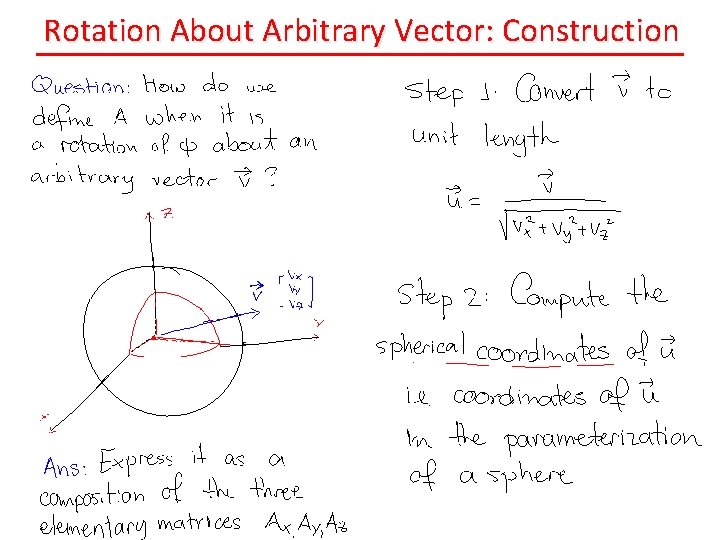
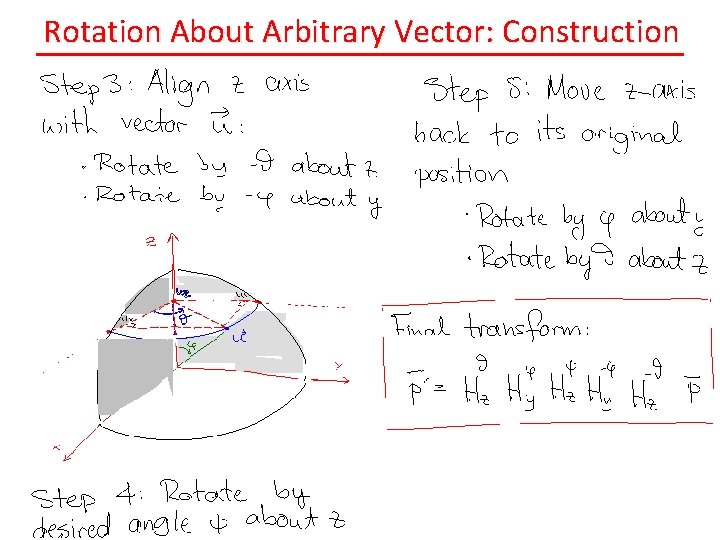
Rotation About Arbitrary Vector: Construction

Rotation About Arbitrary Vector: Construction

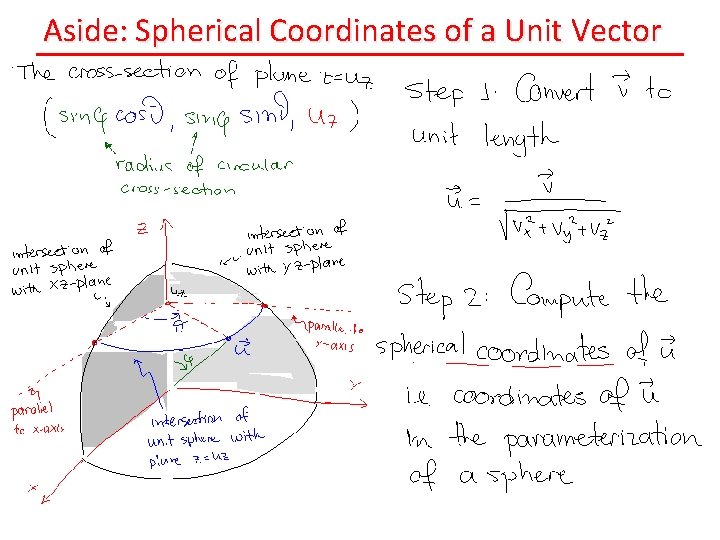
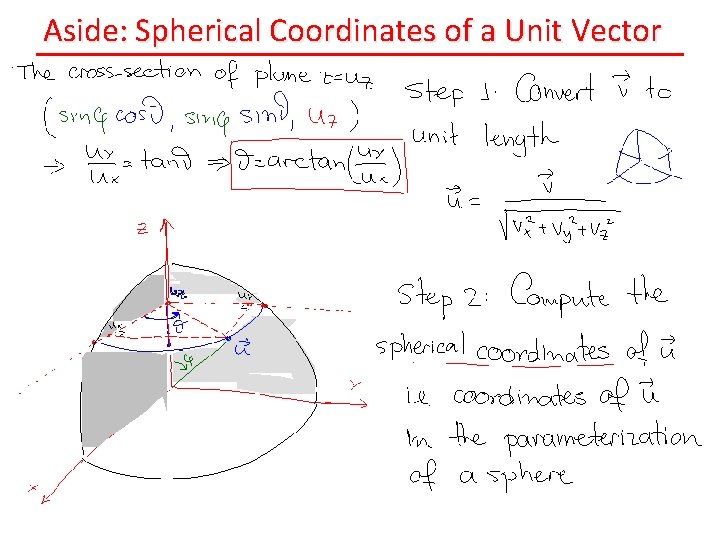
Aside: Spherical Coordinates of a Unit Vector

Aside: Spherical Coordinates of a Unit Vector

Aside: Spherical Coordinates of a Unit Vector

Rotation About Arbitrary Vector: Construction

Rotation About Arbitrary Vector: Construction

Topic 7: 3 D Viewing • Orthographic projection • The world-to-camera transformation • Perspective projection • The transformation chain for 3 D viewing

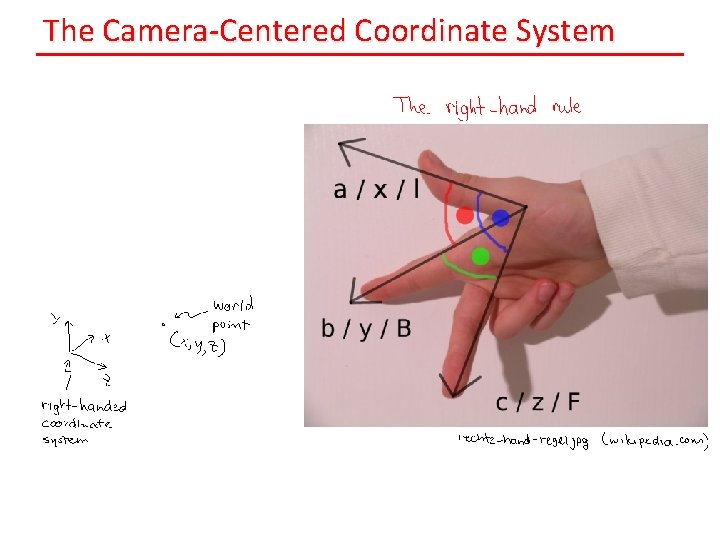
The Camera-Centered Coordinate System

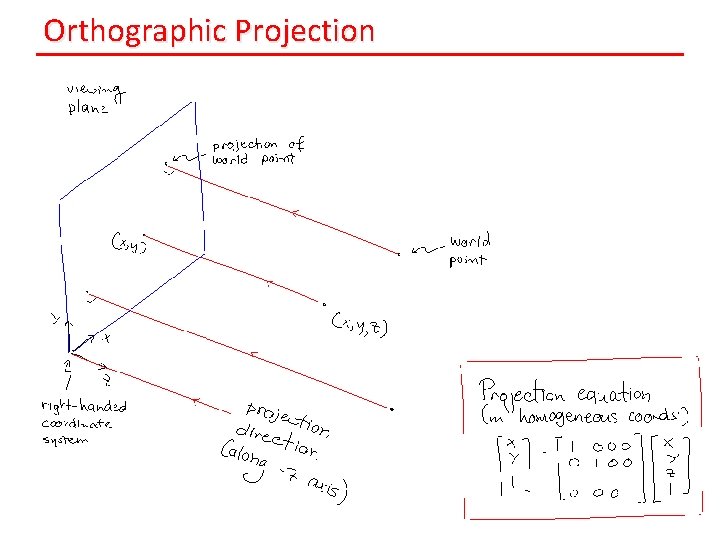
Orthographic Projection

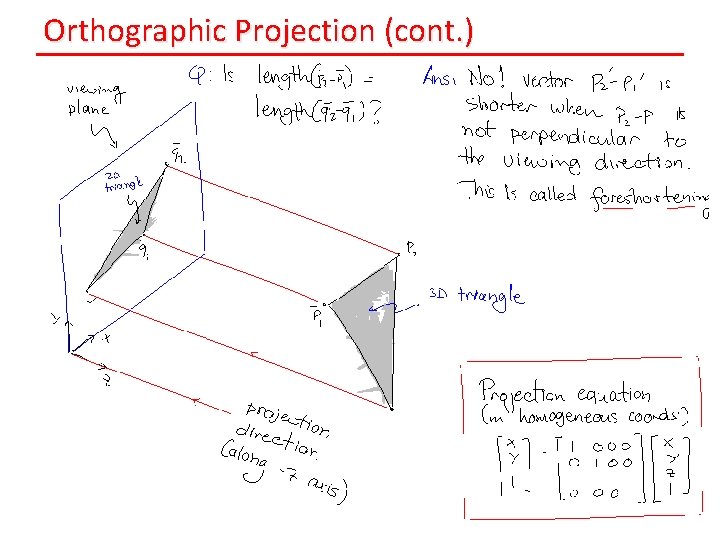
Orthographic Projection (cont. )

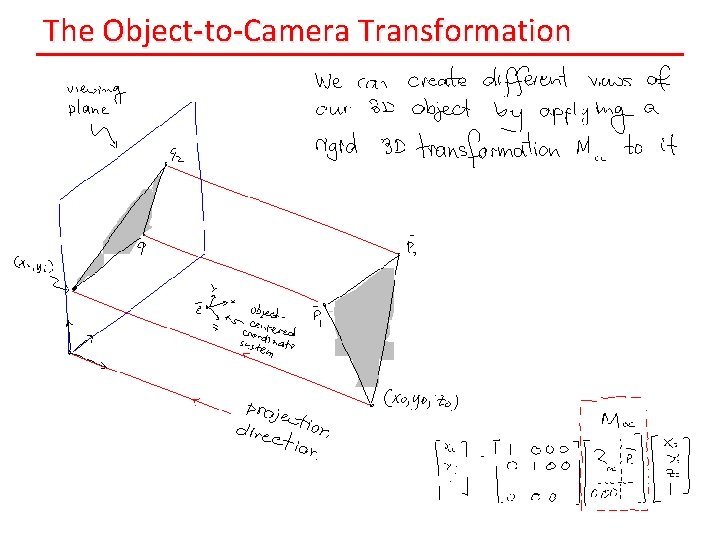
The Object-to-Camera Transformation

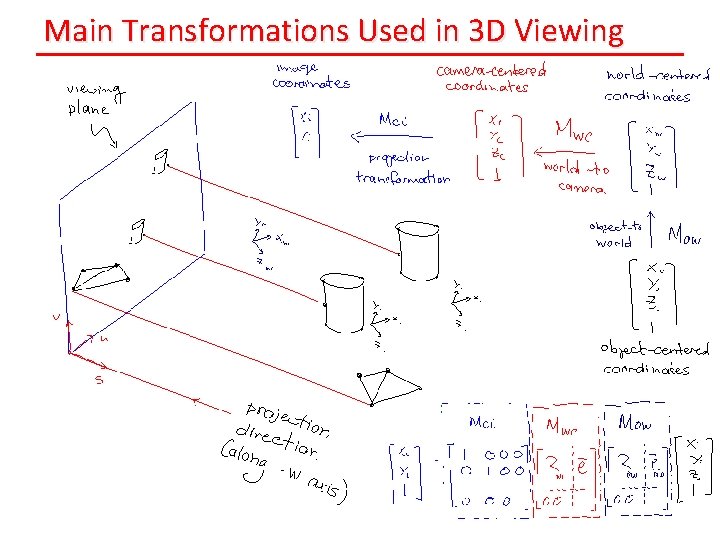
Main Transformations Used in 3 D Viewing

Main Transformations Used in 3 D Viewing

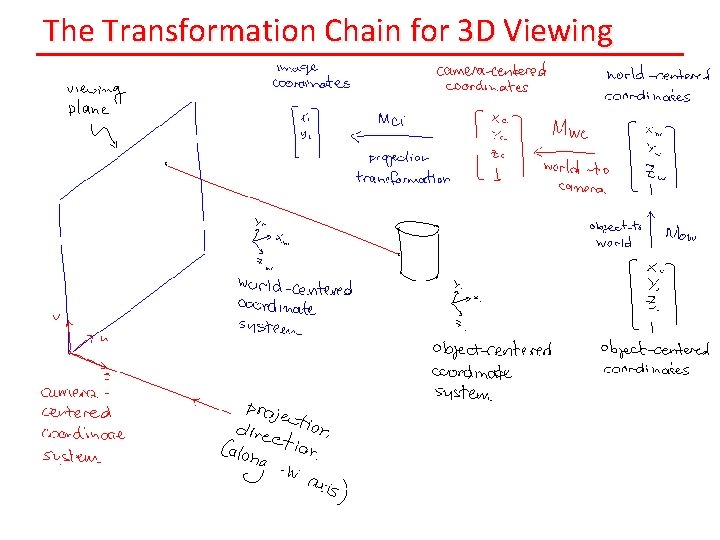
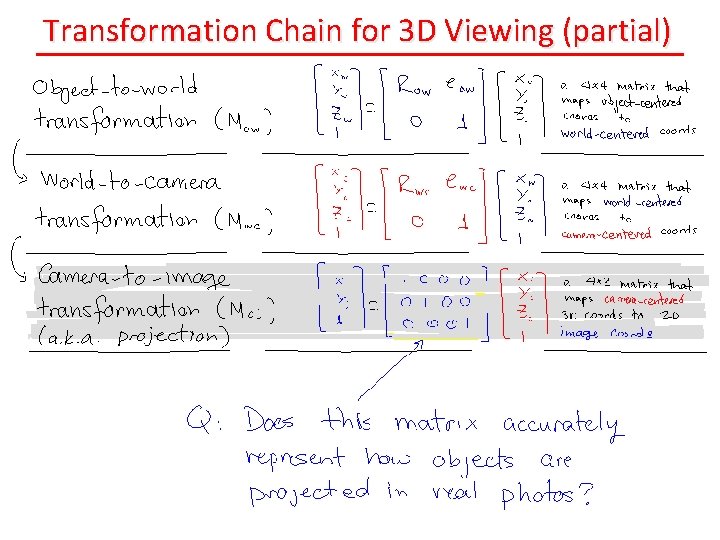
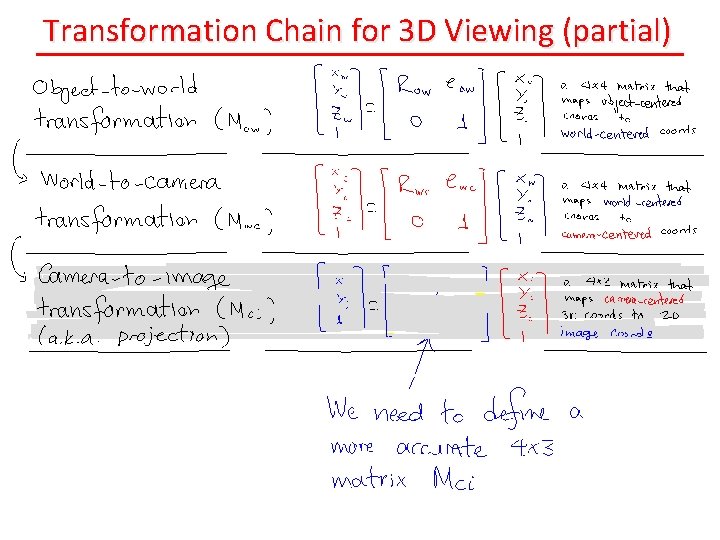
The Transformation Chain for 3 D Viewing

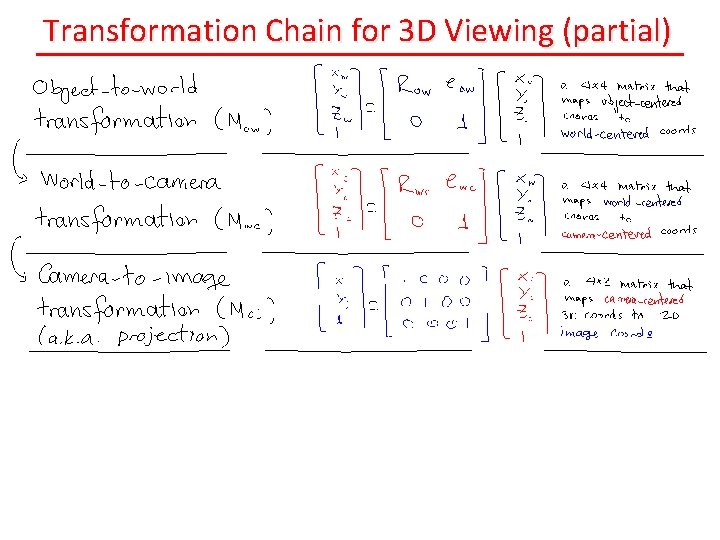
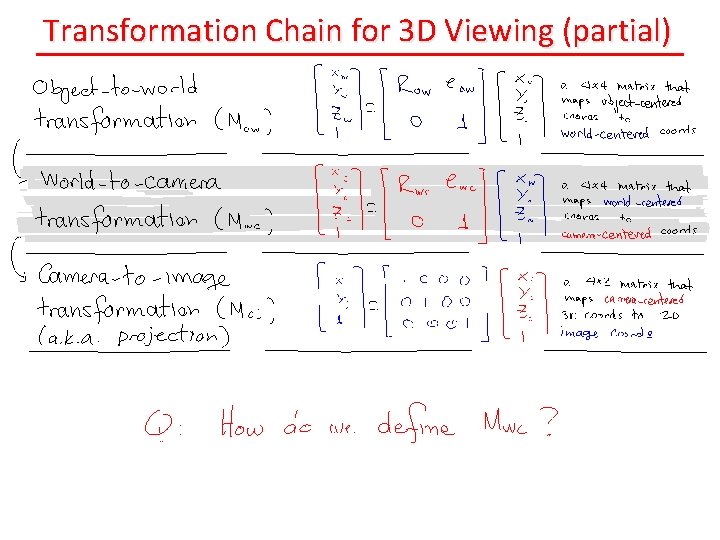
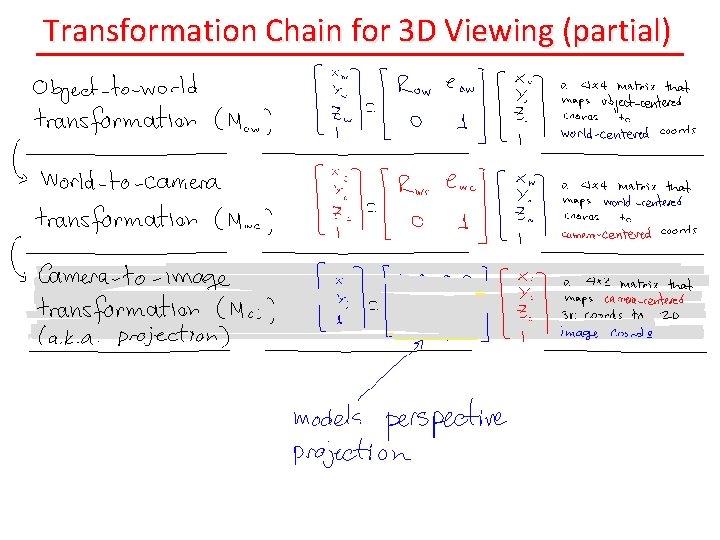
Transformation Chain for 3 D Viewing (partial)

Transformation Chain for 3 D Viewing (partial)

Topic 7: 3 D Viewing • Orthographic projection • The world-to-camera transformation • Perspective projection • The transformation chain for 3 D viewing

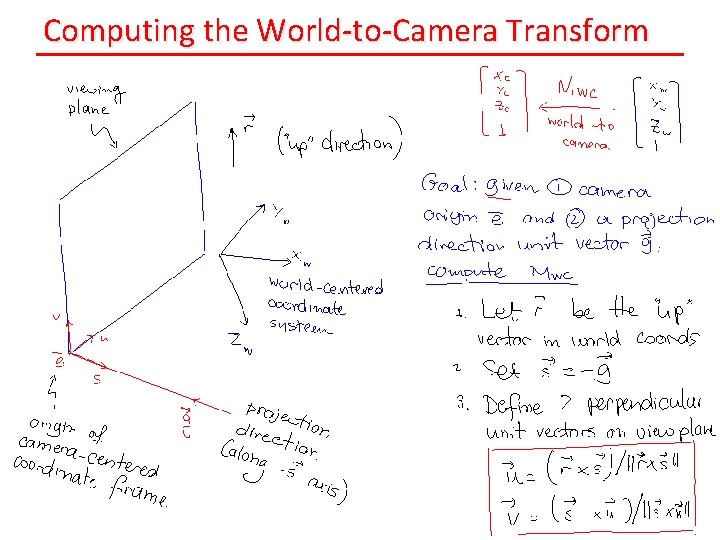
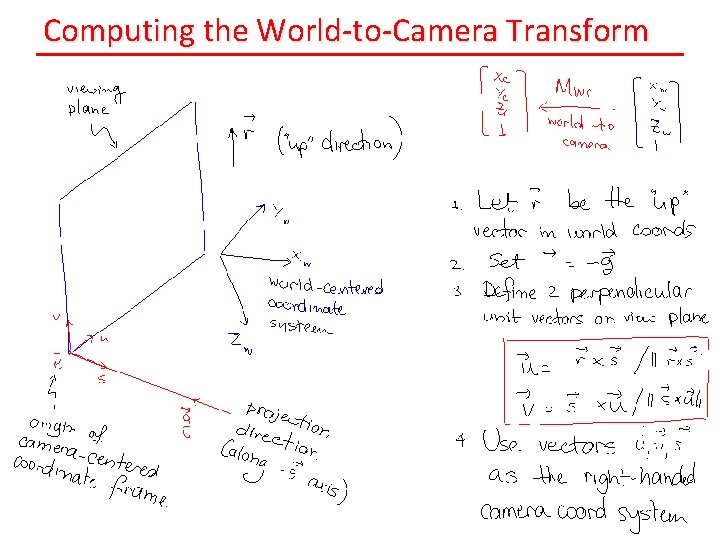
Computing the World-to-Camera Transform

Computing the World-to-Camera Transform

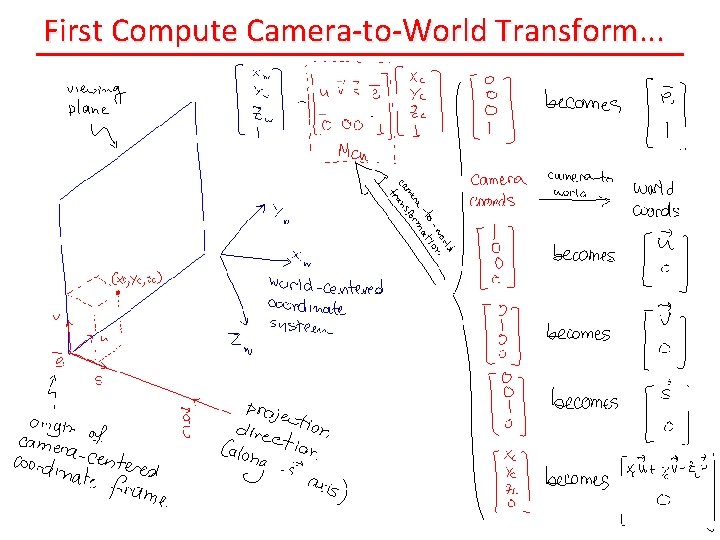
First Compute Camera-to-World Transform. . .

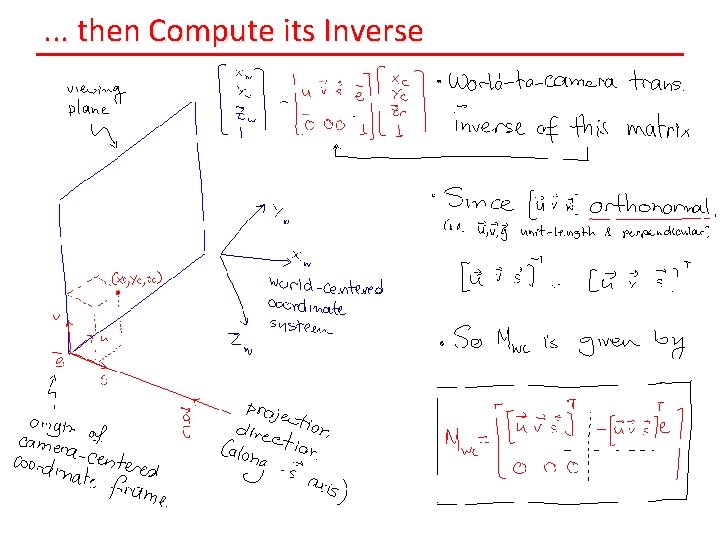
. . . then Compute its Inverse

Transformation Chain for 3 D Viewing (partial)

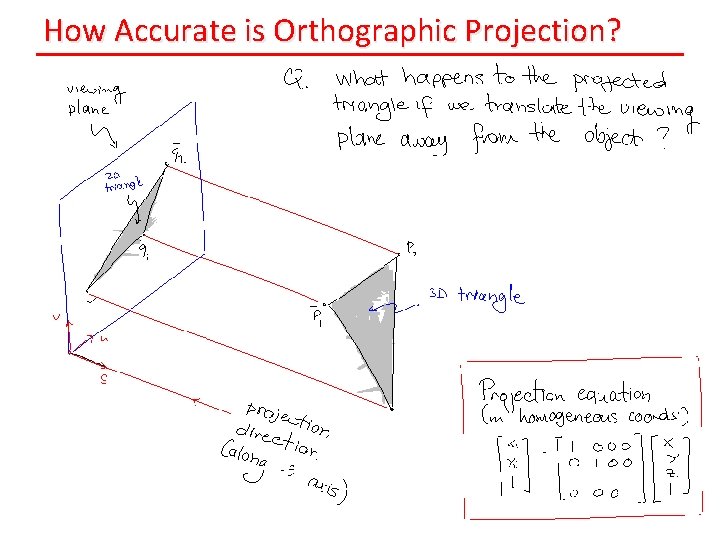
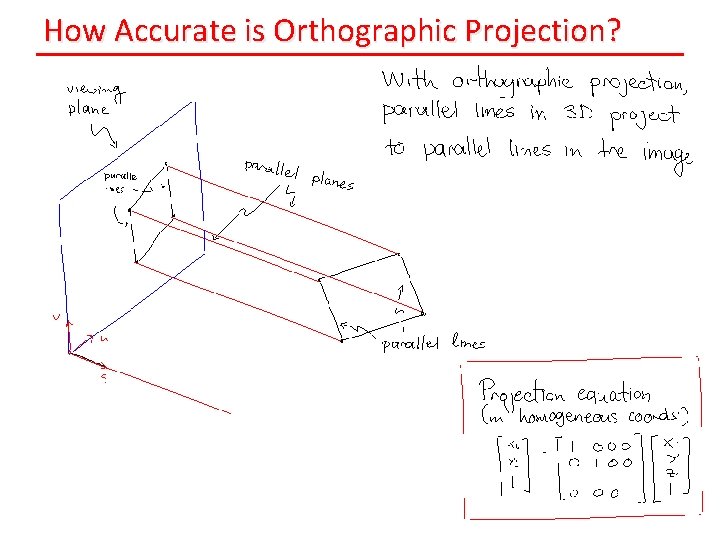
How Accurate is Orthographic Projection?

How Accurate is Orthographic Projection?

Transformation Chain for 3 D Viewing (partial)

Topic 7: 3 D Viewing • Orthographic projection • The world-to-camera transformation • Perspective projection • The transformation chain for 3 D viewing

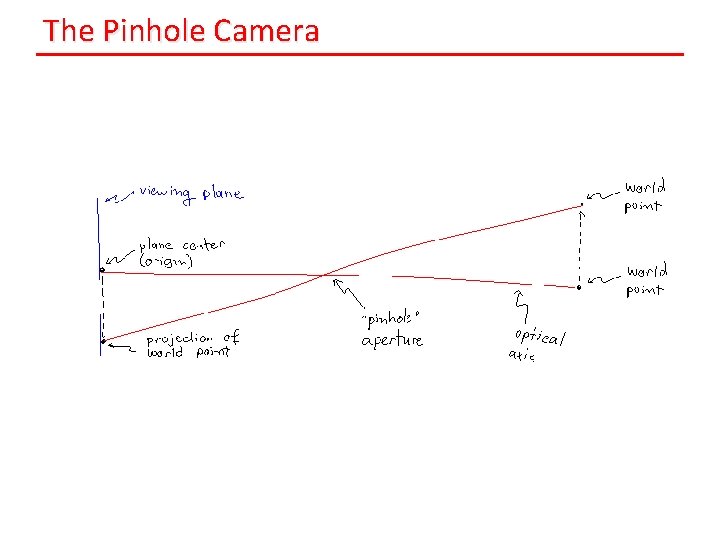
Camera Obscura

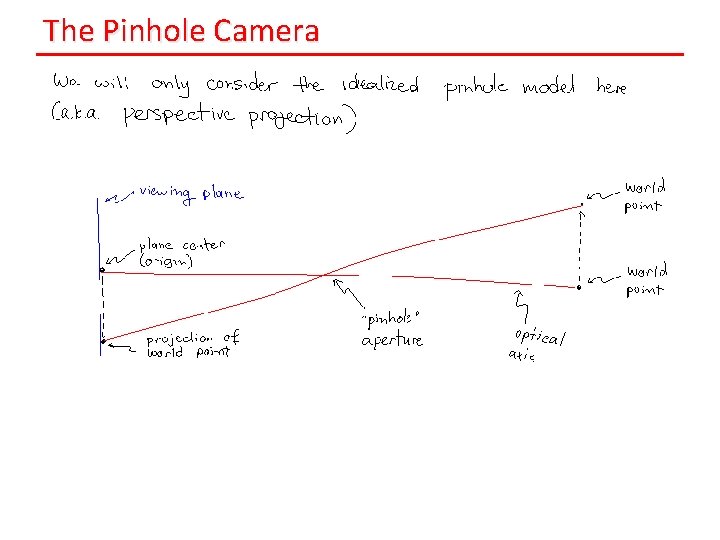
The Pinhole Camera

Camera Obscura

Camera Obscura

Camera Obscura

The Pinhole Camera

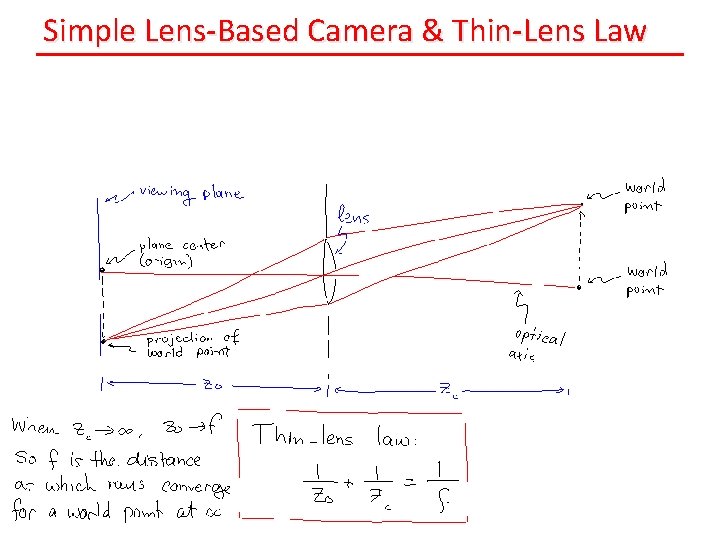
Simple Lens-Based Camera & Thin-Lens Law

Simple Lens-Based Camera & Thin-Lens Law

The Pinhole Camera

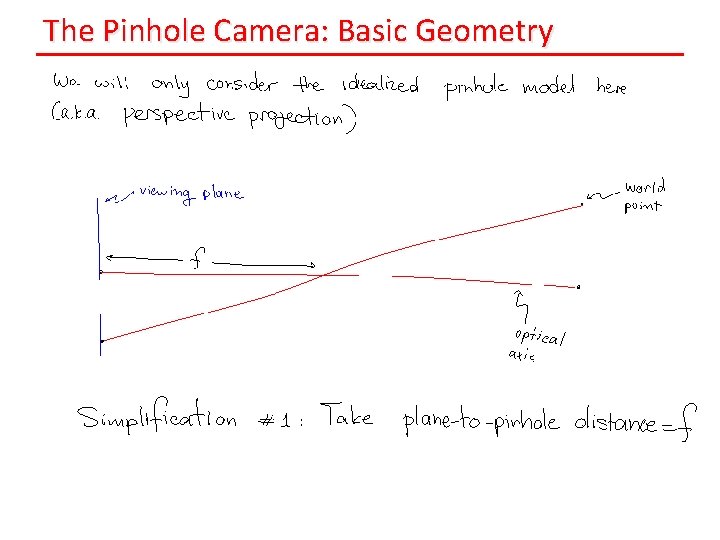
The Pinhole Camera: Basic Geometry

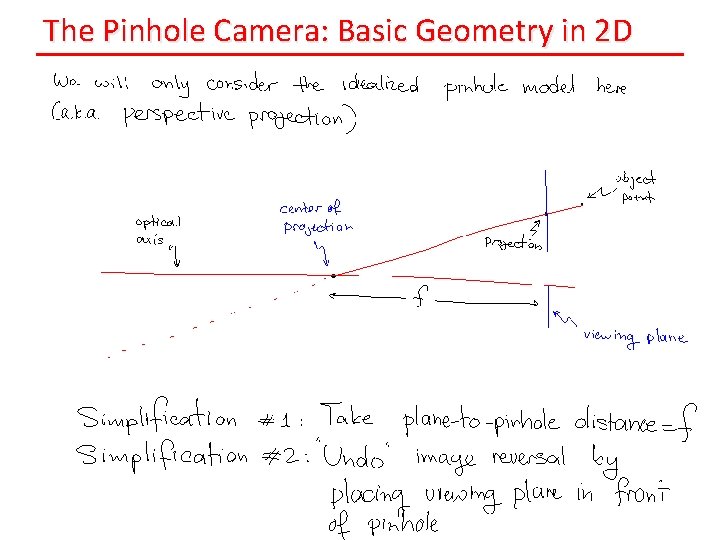
The Pinhole Camera: Basic Geometry in 2 D

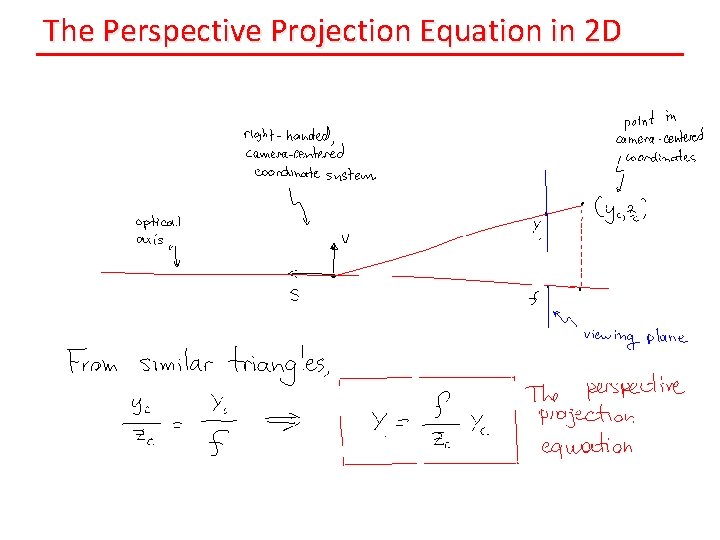
The Perspective Projection Equation in 2 D

The Perspective Projection Equations in 3 D

The Perspective Projection Equations in 3 D

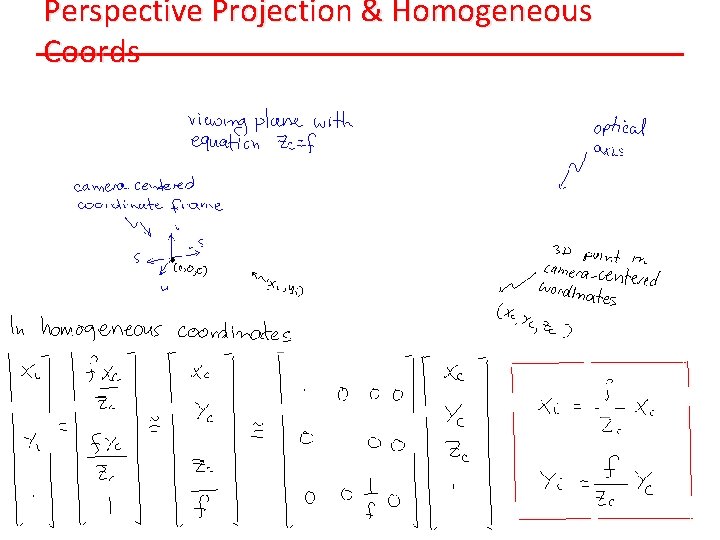
Perspective Projection & Homogeneous Coords

Transformation Chain for 3 D Viewing (partial)

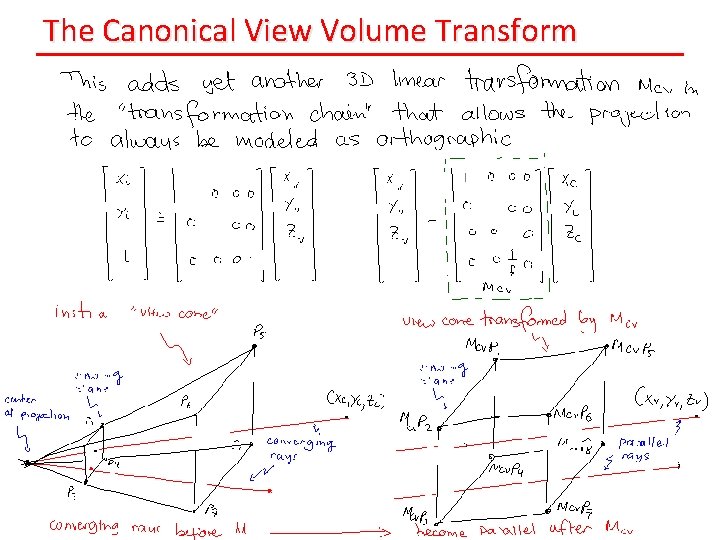
The Canonical View Volume Transform

The Canonical View Volume Transform

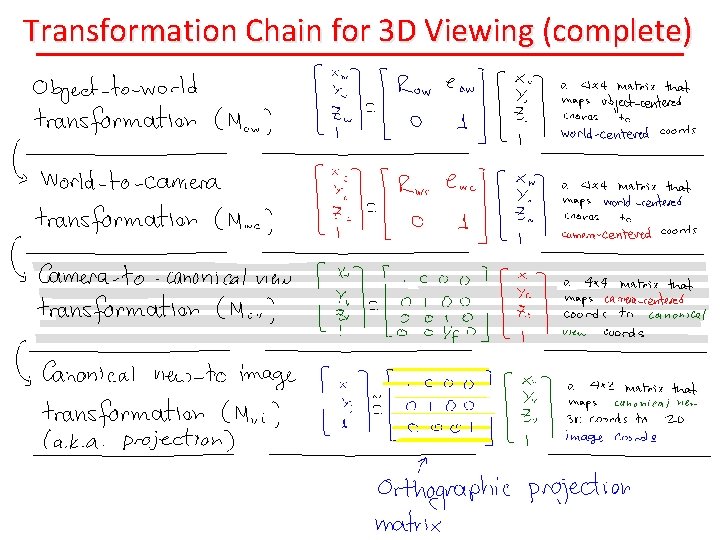
Transformation Chain for 3 D Viewing (complete)