Viewing and Projection Computer Viewing There are three

Viewing and Projection

Computer Viewing • There are three aspects of the viewing process, all of which are implemented in the pipeline, Positioning the camera • Setting the model view matrix Selecting a lens • Setting the projection matrix Clipping • Setting the view volume Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 2

The Open. GL Camera • In Open. GL, initially the world and camera frames are the same Default model view matrix is an identity • The camera is located at origin and points in the negative z direction • Open. GL also specifies a default view volume that is a cube with sides of length 2 centered at the origin Default projection matrix is an identity Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 3

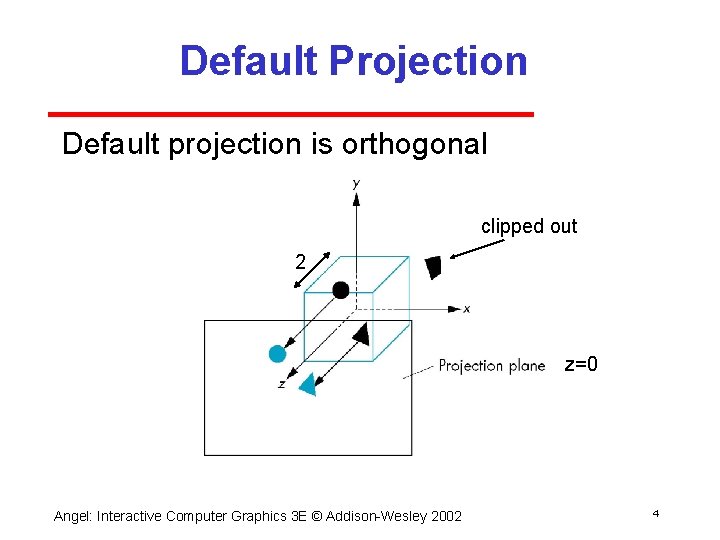
Default Projection Default projection is orthogonal clipped out 2 z=0 Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 4

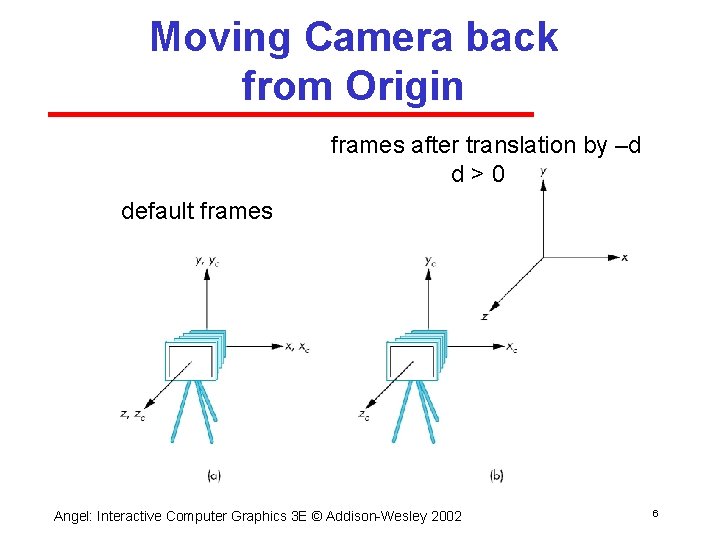
Moving the Camera Frame • If we want to visualize object with both positive and negative z values we can either Move the camera in the positive z direction • Translate the camera frame Move the objects in the negative z direction • Translate the world frame • Both of these views are equivalent and are determined by the model view matrix: Want a translation (gl. Translatef(0. 0, -d); ) d>0 Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 5

Moving Camera back from Origin frames after translation by –d d>0 default frames Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 6

Moving the Camera • We can move the camera to any desired position by a sequence of rotations and translations • Example: side view Rotate the camera Move it away from origin Model view matrix C = TR Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 7

Open. GL code • Remember that last transformation specified is first to be applied • Also, remember that we are transforming the objects, not the camera. gl. Matrix. Mode(GL_MODELVIEW) gl. Load. Identity(); gl. Translatef(0. 0, -d); gl. Rotatef(90. 0, 1. 0, 0. 0); Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 8

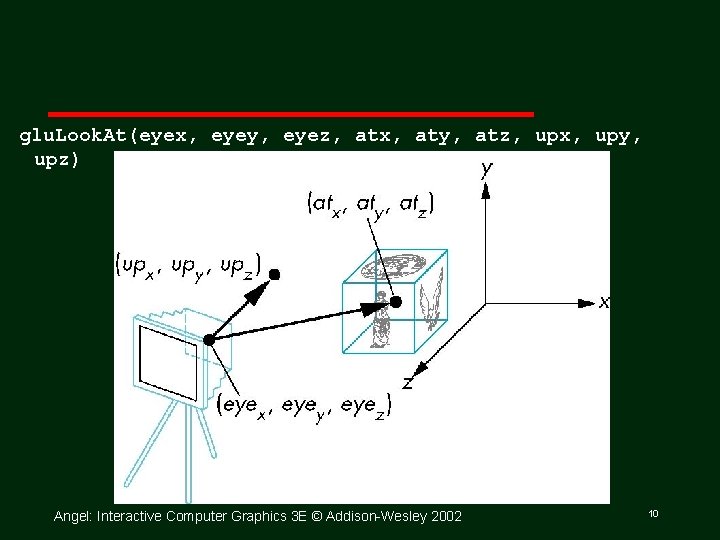
The Look. At Function • The GLU library contains the function gl. Look. At to form the required modelview matrix through a simple interface • Note the need for setting an up direction • Still need to initialize Can concatenate with modeling transformations • Example: isometric view of cube aligned with axes gl. Matrix. Mode(GL_MODELVIEW): gl. Load. Identity(); glu. Look. At(1. 0, 0. , 1. 0. 0. 0); Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 9

glu. Look. At(eyex, eyey, eyez, atx, aty, atz, upx, upy, upz) Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 10

Other Viewing APIs • The Look. At function is only one possible API for positioning the camera • Others include Yaw, pitch, roll Elevation, azimuth, twist Direction angles Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 11

• Now, we have determined how the objects are placed relative to the camera. • But we haven’t defined how the objects are projected to the image.

(Orthogonal) Projection and Normalization • The default projection in the eye (camera) frame is orthogonal • For points within the default view volume xp = x yp = y zp = 0 • Most graphics systems use view normalization All other views are converted to the default view by transformations that determine the projection matrix Allows use of the same pipeline for all views Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 13

Homogeneous Coordinate Representation xp = x yp = y zp = 0 wp = 1 pp = Mp M= In practice, we can let M = I and set the z term to zero later Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 14

Perspective Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 15

Simple Perspective • Center of projection at the origin • Projection plane z = d, d < 0 Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 16

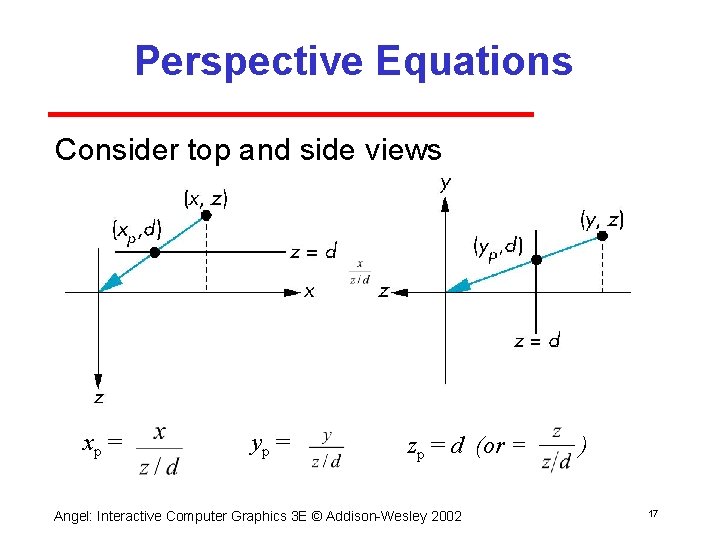
Perspective Equations Consider top and side views xp = yp = zp = d (or = Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 ) 17

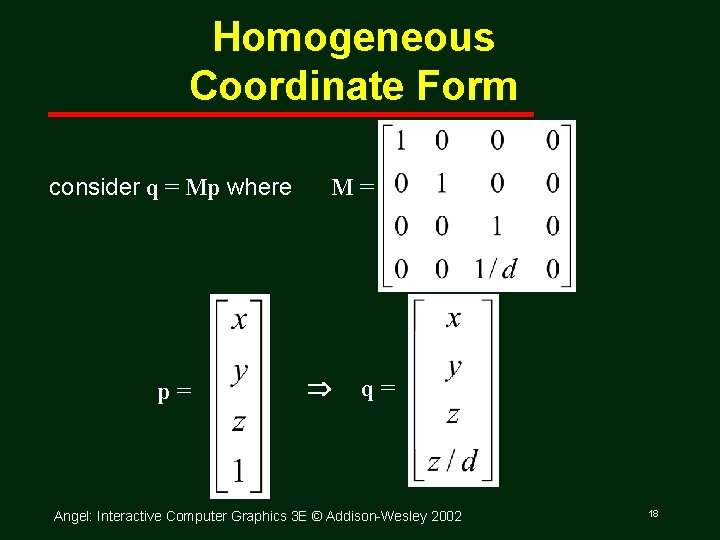
Homogeneous Coordinate Form consider q = Mp where p= M= q= Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 18

Perspective Division • However w 1, so we must divide by w to return from homogeneous coordinates • This perspective division yields xp = yp = zp = d = the desired perspective equations • We will consider the corresponding clipping volume with the Open. GL functions Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 19

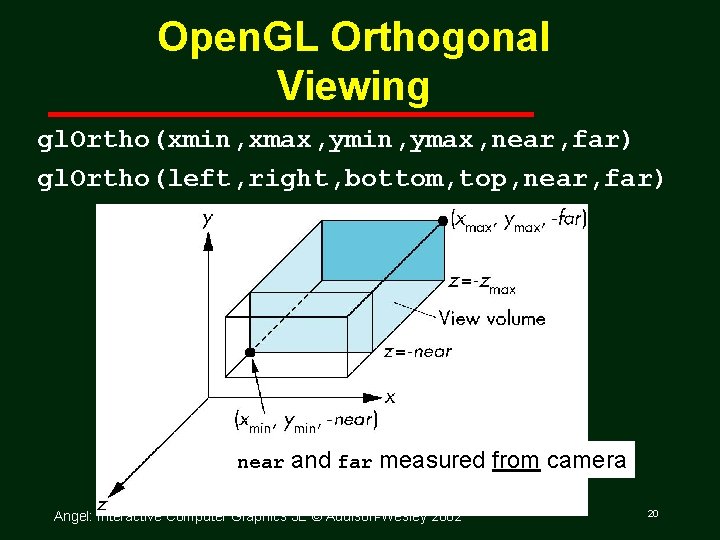
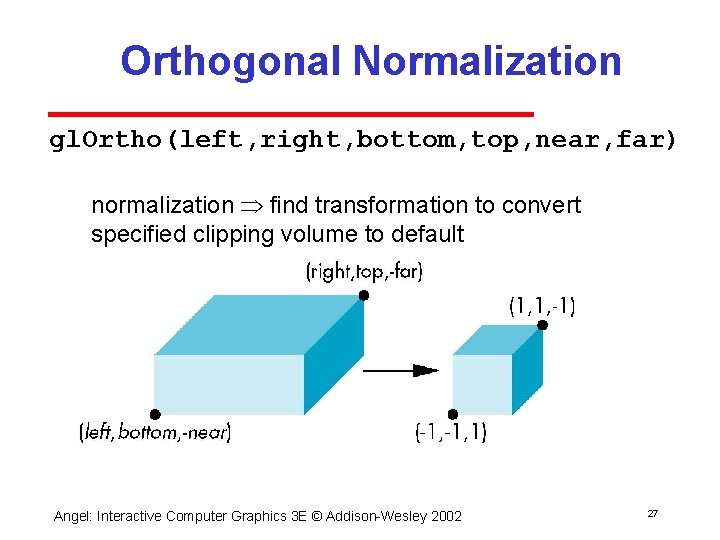
Open. GL Orthogonal Viewing gl. Ortho(xmin, xmax, ymin, ymax, near, far) gl. Ortho(left, right, bottom, top, near, far) near and far measured from camera Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 20

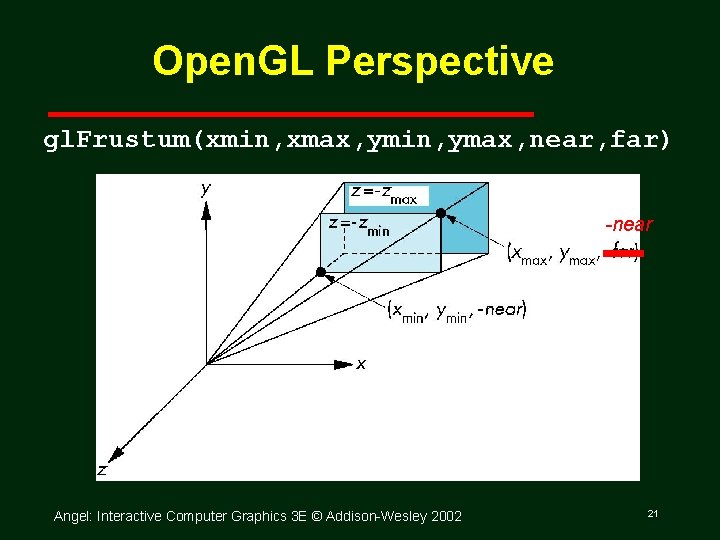
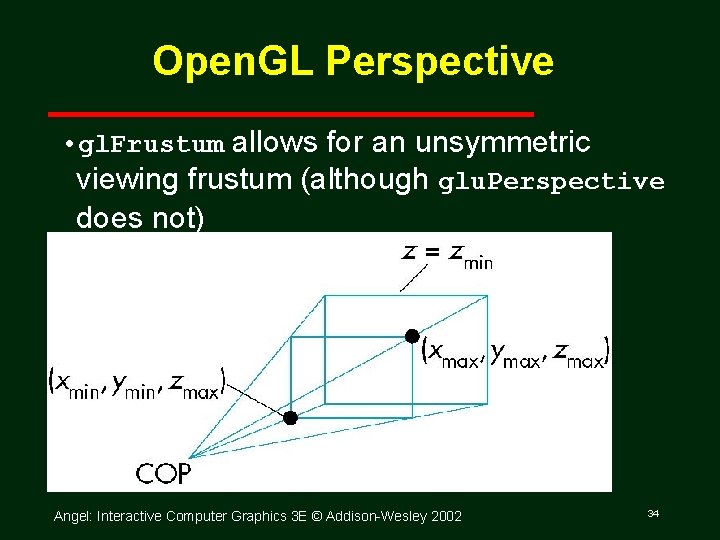
Open. GL Perspective gl. Frustum(xmin, xmax, ymin, ymax, near, far) -near Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 21

Using Field of View • With gl. Frustum it is often difficult to get the desired view • glu. Perpective(fovy, aspect, near, far) often provides a better interface front plane aspect = w/h Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 22

Now, we will look at how the Open. GL projection matrices are computed…

Normalization • Rather than derive a different projection matrix for each type of projection, we can convert all projections to orthogonal projections with the default view volume • This strategy allows us to use standard transformations in the pipeline and makes for efficient clipping Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 24

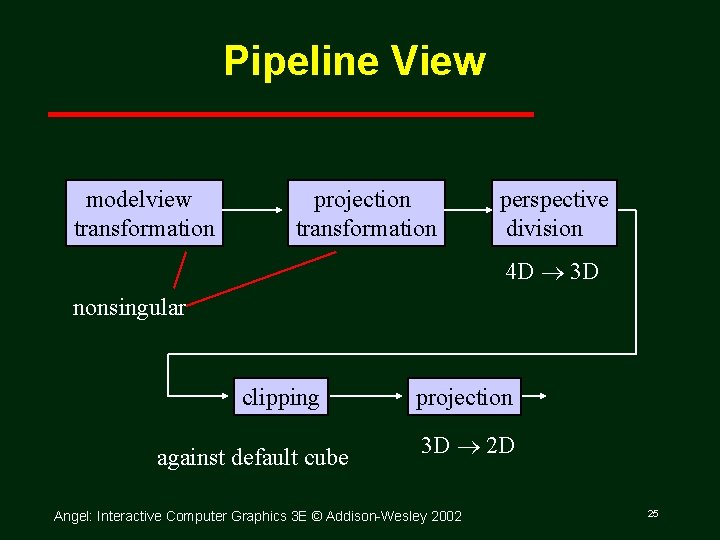
Pipeline View modelview transformation projection transformation perspective division 4 D 3 D nonsingular clipping against default cube projection 3 D 2 D Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 25

Notes • We stay in four dimensional homogeneous coordinates through both the modelview and projection transformations Both these transformations are nonsingular Default to identity matrices (orthogonal view) • Normalization lets us clip against simple cube regardless of type of projection • Delay final projection until end Important for hidden surface removal to retain depth information as long as possible Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 26

Orthogonal Normalization gl. Ortho(left, right, bottom, top, near, far) normalization find transformation to convert specified clipping volume to default Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 27

Orthogonal Matrix • Two steps Move center to origin T(-(left+right)/2, -(bottom+top)/2, (near+far)/2)) Scale to have sides of length 2 S(2/(left-right), 2/(top-bottom), 2/(near-far)) P = ST = Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 28

Final Projection • Set z =0 • Equivalent to the homogeneous coordinate transformation Morth = • Hence, general orthogonal projection in 4 D is P = Morth. ST Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 29

Perspective in Open. GL • gl. Frustum( left, right, bottom, top, near, far ) • glu. Perpective( FOV_vertical, aspect_ratio, near, far ) Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 30

Simple Perspective Consider a simple perspective with the COP at the origin, the near clipping plane at z = 1, and a 90 degree field of view determined by the planes x = z, y = z Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 31

Perspective Matrices Simple projection matrix in homogeneous coordinates M= Note that this matrix is independent of the far clipping plane Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 32

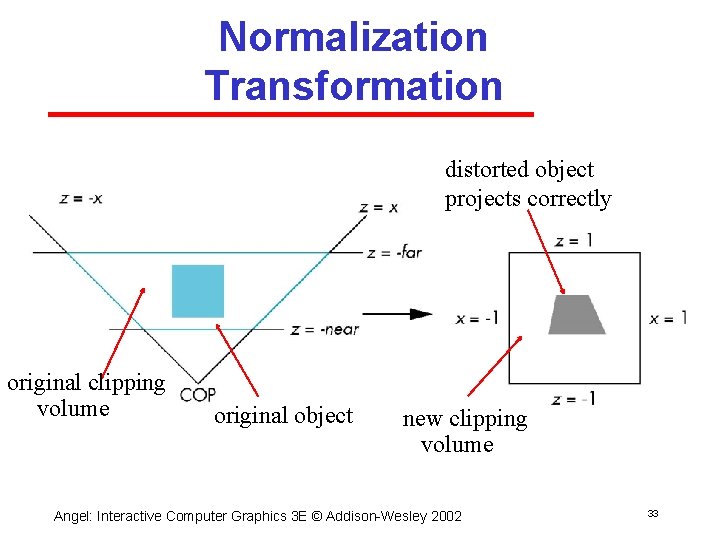
Normalization Transformation distorted object projects correctly original clipping volume original object new clipping volume Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 33

Open. GL Perspective • gl. Frustum allows for an unsymmetric viewing frustum (although glu. Perspective does not) Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 34

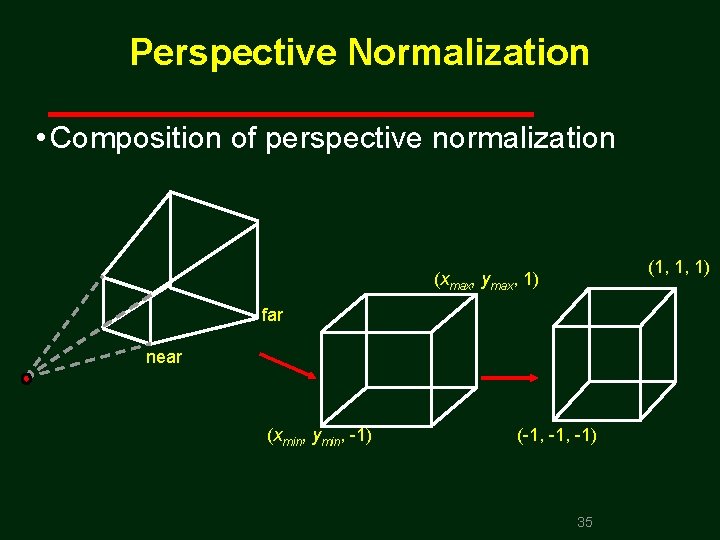
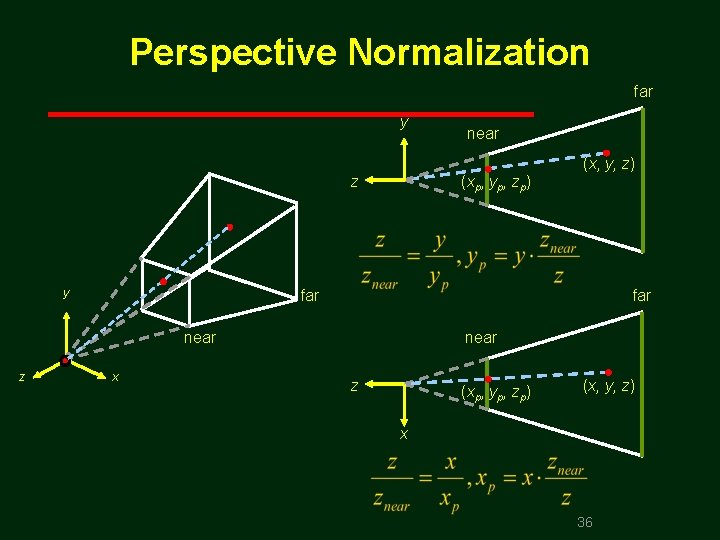
Perspective Normalization • Composition of perspective normalization (1, 1, 1) (xmax, ymax, 1) far near (xmin, ymin, 1) ( 1, 1) 35

Perspective Normalization far y near (x, y, z) z y (xp, yp, zp) far near z x near z (xp, yp, zp) (x, y, z) x 36

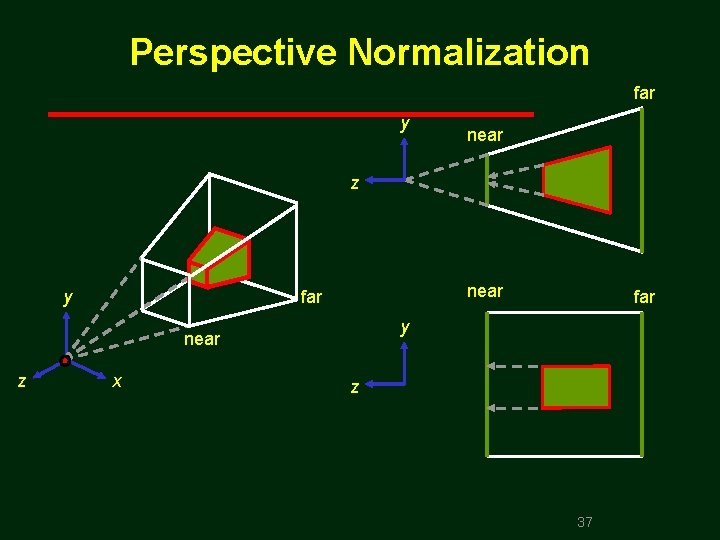
Perspective Normalization far y near z y near far y near z x far z 37

Perspective Normalization 38

Perspective Normalization • Composition of orthogonal normalization 39

Perspective Normalization 40

Why do we do it this way? • Normalization allows for a single pipeline for both perspective and orthogonal viewing • We keep in four dimensional homogeneous coordinates as long as possible to retain three dimensional information needed for hidden surface removal and shading • We simplify clipping Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 41

Generalization N= after persepective divison, the point (x, y, z, 1) goes to x’’ = x/z y’’ = y/z z’’ = -(a+b/z) which projects orthogonally to the desired point regardless of a and b Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 42

Picking a and b If we pick a= b= the near plane is mapped to z = -1 the far plane is mapped to z =1 and the sides are mapped to x = 1, y = 1 Hence the new clipping volume is the default clipping volume Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 43

Now let’s look at the Z more carefully… Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 44

Normalization and Hidden -Surface Removal • Although our selection of the form of the perspective matrices may appear somewhat arbitrary, it was chosen so that if z 1 > z 2 in the original clipping volume then the z’s for the transformed points z 1’ > z 2’ • Thus hidden surface removal works if we first apply the normalization transformation • However, the formula z’’ = -(a+b/z) implies that the distances are distorted by the normalization which can cause numerical problems especially if the near distance is small Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 45

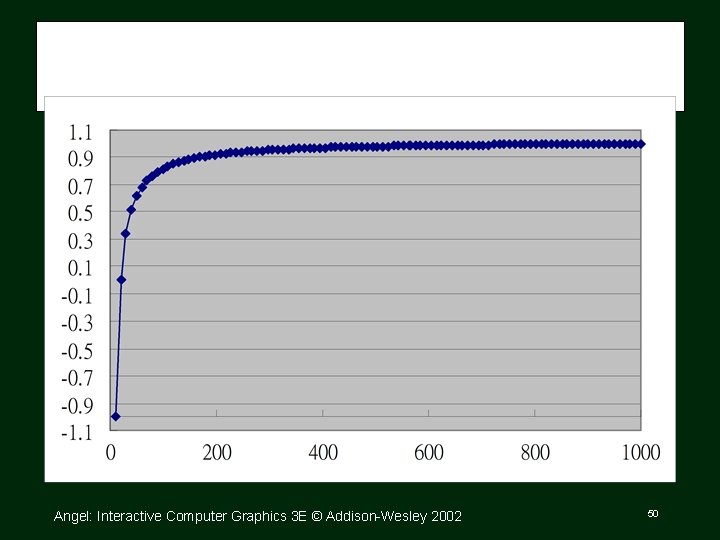
The Z Component • So far, we have ignored the Z coordinate. • We want to convert Z so that the range of [near, far] becomes [ 1, 1] • Note that this is NOT a “uniform” scaling. We will see why after a few slides. Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 46

Range of Z • If Z = near, what is Z’? 1 • If Z = far, what is Z’? 1 • Does Z’ change linearly with Z? No! Let a= b= Z’ = Zw / w = (a*Z+b) / Z = a + b/Z Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 47

Why Not Linear? • To make it linear, we will have to make WZ’ = a*Z 2 + b. Z (so that Z’ = WZ’/W = a*Z + b) • But that’s impossible with the 4 x 4 perspective matrix… Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 48

Z Resolution • Since screen Z’ is expressed in the form of a+b/Z, most of the Z resolution is used up by the Z’s closer to the near plane. • So, what does this mean? • You should NOT set z. Near to be very close to the eye position. Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 49

Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 50

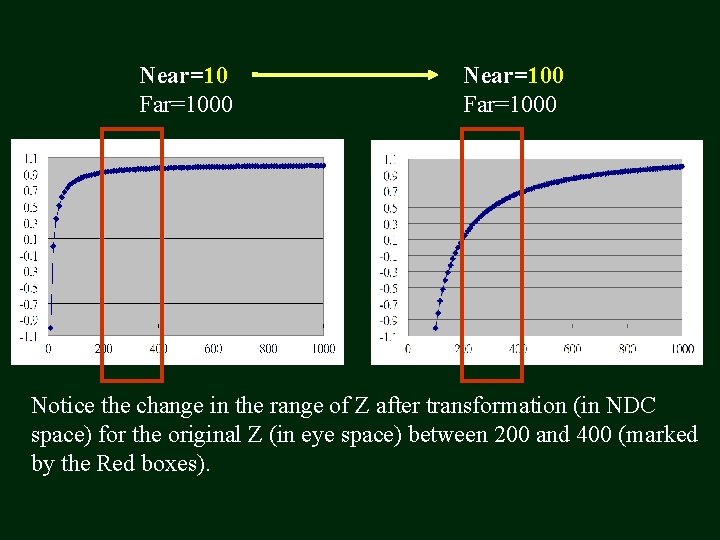
Near=10 Far=1000 Near=100 Far=1000 Notice the change in the range of Z after transformation (in NDC space) for the original Z (in eye space) between 200 and 400 (marked by the Red boxes).

Now, some more math… Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 52

Transformation of Normals • Transformation does not necessarily preserve the normal vectors. If a. b=0, does T(a). T(b)=0 also? • For example: what happen if we scale (X, Y) by (0. 5, 1. 0) in a 2 D image? Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 53

We shouldn’t transform the two end points of a normal vector. What we should do is to transform (three points of) the plane first, then find its normal. What does that mean in math? (See Appendix F of the Open. GL red book. ) Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 54

Transformation of Normals • (Foley/van. Dam pages 216 217) NT. P = 0 but is (MN)T. MP=0? Not always!! Let (QN)T. MP=0 (i. e. , transform P first, then try to find its normal) NTQTMP=0 So QTM=I QT= M 1 or Q=(M 1)T • Special case when M 1=MT If M consists of only the composition of rotation, translation, and uniform scaling. Q=M Angel: Interactive Computer Graphics 3 E © Addison Wesley 2002 55