Projective Geometry and Camera model Class 2 points

Projective Geometry and Camera model Class 2 points, lines, planes conics and quadrics transformations camera model Read tutorial chapter 2 and 3. 1 http: //www. cs. unc. edu/~marc/tutorial/ Chapter 1, 2 and 5 in Hartley and Zisserman

Homogeneous coordinates Homogeneous representation of 2 D points and lines The point x lies on the line l if and only if Note that scale is unimportant for incidence relation equivalence class of vectors, any vector is representative Set of all equivalence classes in R 3 (0, 0, 0)T forms P 2 Homogeneous coordinates Inhomogeneous coordinates but only 2 DOF

Points from lines and vice-versa Intersections of lines The intersection of two lines and is Line joining two points The line through two points Example and is Note: with

Ideal points and the line at infinity Intersections of parallel lines Example tangent vector normal direction Ideal points Line at infinity • Line at infinity is a collection of all the points at infinity as x 1/x 2 varies, i. e. all Possible directions Note that in P 2 there is no distinction between ideal points and others

3 D points and planes Homogeneous representation of 3 D points and planes The point X lies on the plane π if and only if The plane π goes through the point X if and only if

Planes from points (solve as right nullspace of )

Points from planes (solve as right nullspace of Representing a plane by its span • M is 4 x 3 matrix. Columns of M are null space of )

Lines • Line is either joint of two points or intersection of two planes Representing a line by its span: two (4 dof) vectors A, B for two space points Dual representation: P and Q are planes; line is span of row space of Example: X-axis (Alternative: Plücker representation, details see e. g. H&Z)

Points, lines and planes • Plane defined by join of point X and line W is the null space of M • Point X defined by the intersection of line W with plane is the null space of M

Conics Curve described by 2 nd-degree equation in the plane or homogenized or in matrix form with 5 DOF:

Five points define a conic For each point the conic passes through or stacking constraints yields Conic c is a null vector of the above matrix

Tangent lines to conics The line l tangent to C at point x on C is given by l=Cx x l C

Dual conics A line tangent to the conic C satisfies In general (C full rank): Dual conics = line conics = conic envelopes Points conic lie on a point lines are tangent to the point conic C; conic C is the envelope of lines l

Degenerate conics A conic is degenerate if matrix C is not of full rank e. g. two lines (rank 2) e. g. repeated line (rank 1) Degenerate line conics: 2 points (rank 2), double point (rank 1) Note that for degenerate conics

Quadrics and dual quadrics (Q : 4 x 4 symmetric matrix) • • 9 d. o. f. in general 9 points define quadric det Q=0 ↔ degenerate quadric tangent plane • Dual Quadric: defines equation on planes • relation to quadric (non-degenerate)

2 D projective transformations Definition: A projectivity is an invertible mapping h from P 2 to itself such that three points x 1, x 2, x 3 lie on the same line if and only if h(x 1), h(x 2), h(x 3) do. Theorem: A mapping h: P 2 is a projectivity if and only if there exist a non-singular 3 x 3 matrix H such that for any point in P 2 reprented by a vector x it is true that h(x)=Hx Definition: Projective transformation or 8 DOF projectivity=collineation=projective transformation=homography

Transformation of 2 D points, lines and conics For a point transformation Transformation for lines Transformation for conics Transformation for dual conics

Fixed points and lines (eigenvectors H =fixed points) ( 1= 2 pointwise fixed line) (eigenvectors H-T =fixed lines)

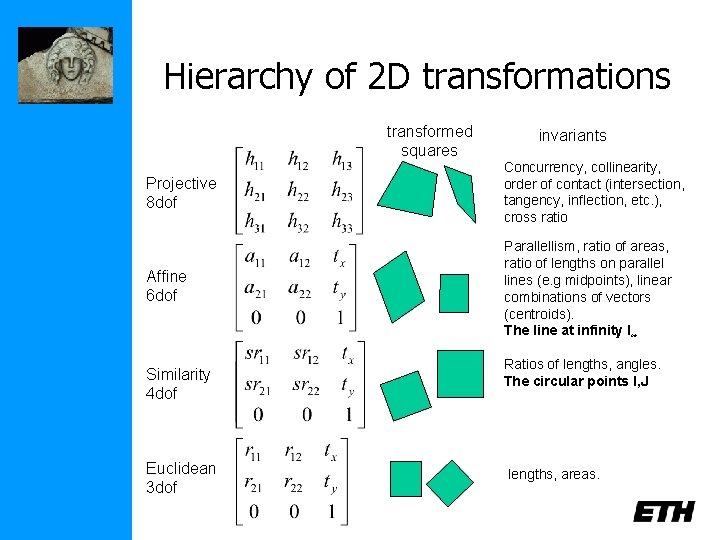
Hierarchy of 2 D transformations transformed squares invariants Projective 8 dof Concurrency, collinearity, order of contact (intersection, tangency, inflection, etc. ), cross ratio Affine 6 dof Parallellism, ratio of areas, ratio of lengths on parallel lines (e. g midpoints), linear combinations of vectors (centroids). The line at infinity l∞ Similarity 4 dof Euclidean 3 dof Ratios of lengths, angles. The circular points I, J lengths, areas.

Projective geometry of 1 D The cross ratio Is invariant under projective transformations in P^1. Four sets of four collinear points; each set is related to the others by a line projectivity Since cross ratio is an invariant under projectivity, the cross ratio has the same value for all the sets shown

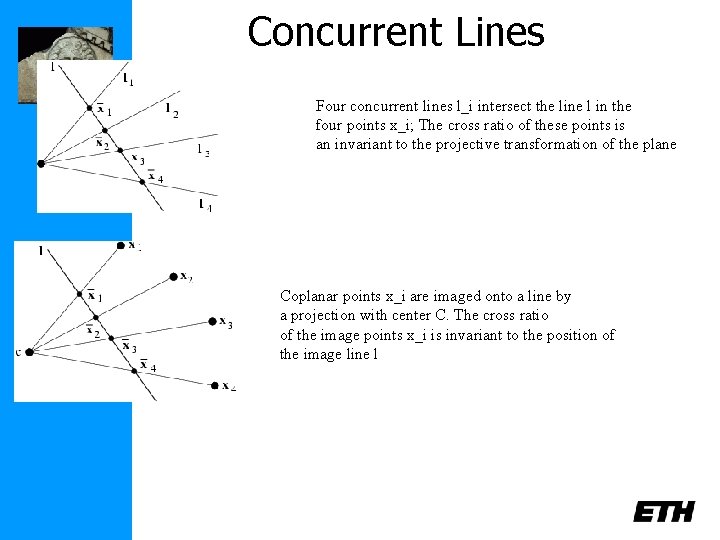
Concurrent Lines Four concurrent lines l_i intersect the line l in the four points x_i; The cross ratio of these points is an invariant to the projective transformation of the plane Coplanar points x_i are imaged onto a line by a projection with center C. The cross ratio of the image points x_i is invariant to the position of the image line l

A hierarchy of transformations • Euclidean transformations (rotation and translation) leave distances unchanged • Similarity: circle imaged as circle; square as square; parallel or perpendicular lines have same relative orientation • Affine: circle becomes ellipse; orthogonal world lines not imaged as orthogonoal; But, parallel lines in the square remain parallel • Projective: parallel world lines imaged as converging lines; tiles closer to camera larger image than those further away. Similarity Affine projective

The line at infinity l is a fixed line under a projective transformation H if and only if H is an affinity Note: not fixed pointwise

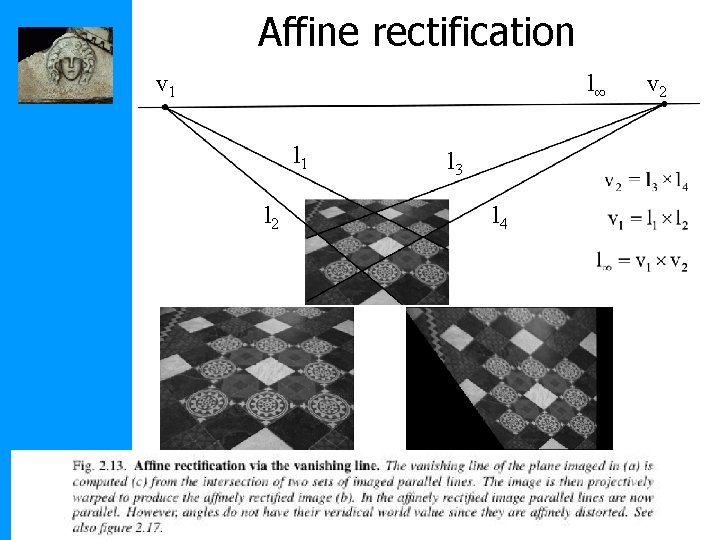
Affine properties from images projection rectification Two step process: 1. Find l the image of line at infinity in plane 2 2. Plug into H_pa Image of line at infinity in plane

Affine rectification l∞ v 1 l 2 l 3 l 4 v 2

The circular points Two points on l_inf which are fixed under any similarity transformation Canonical coordinates of circular points The circular points I, J are fixed points under the projective transformation H iff H is a similarity

The circular points Two points on l_inf: Every circle intersects l_inf at circular points “circular points” Circle: Line at infinity Algebraically, encodes orthogonal directions l∞

Conic dual to the circular points l∞ The dual conic is fixed conic under the projective transformation H iff H is a similarity Note: has 4 DOF (3 x 3 ho mogeneous; symmetric, determinant is zero) l∞ is the nullvector

Angles Euclidean: Projective: (1) (l and m orthogonal) Once is identified in the projective plane, then Euclidean angles may be measured by equation (1)

Transformation of 3 D points, planes and quadrics For a point transformation Transformation for lines Transformation for conics Transformation for dual conics (cfr. 2 D equivalent)

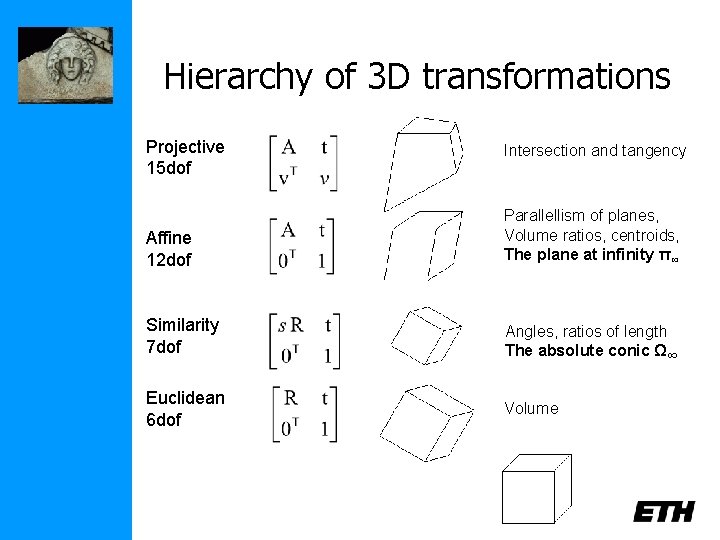
Hierarchy of 3 D transformations Projective 15 dof Affine 12 dof Similarity 7 dof Euclidean 6 dof Intersection and tangency Parallellism of planes, Volume ratios, centroids, The plane at infinity π∞ Angles, ratios of length The absolute conic Ω∞ Volume

The plane at infinity π is a fixed plane under a projective transformation H iff H is an affinity 1. 2. 3. 4. canonical position contains directions two planes are parallel line of intersection in π∞ line // line (or plane) point of intersection in π∞

The absolute conic Ω∞ is a (point) conic on π. In a metric frame: or conic for directions: (with no real points) The absolute conic Ω∞ is a fixed conic under the projective transformation H iff H is a similarity 1. Ω∞ is only fixed as a set 2. Circle intersect Ω∞ in two circular points 3. Spheres intersect π∞ in Ω∞

The absolute dual quadric Set of planes tangent to an ellipsoid, then squash to a pancake The absolute dual quadric Ω*∞ is a fixed conic under the projective transformation H iff H is a similarity 1. 8 dof ( symmetric matrix, det is zero) 2. plane at infinity π∞ is the nullvector of Ω∞ 3. Angles:

Camera model Relation between pixels and rays in space ?

Pinhole camera

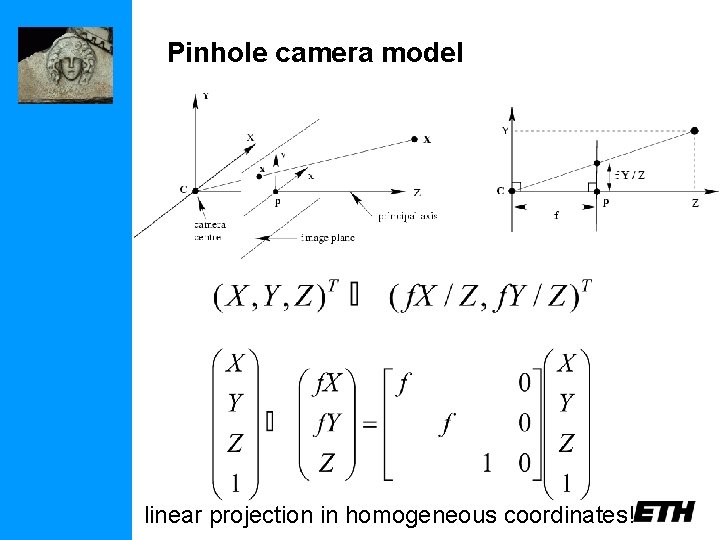
Pinhole camera model linear projection in homogeneous coordinates!

Pinhole camera model

Principal point offset principal point

Principal point offset calibration matrix

Camera rotation and translation ~

CCD camera

General projective camera 11 dof (5+3+3) non-singular intrinsic camera parameters extrinsic camera parameters

Radial distortion • Due to spherical lenses (cheap) • Model: R R straight lines are not straight anymore http: //foto. hut. fi/opetus/260/luennot/11/atkinson_6 -11_radial_distortion_zoom_lenses. jpg

Camera model Relation between pixels and rays in space ?

Projector model Relation between pixels and rays in space (dual of camera) ? (main geometric difference is vertical principal point offset to reduce keystone effect)

Meydenbauer camera vertical lens shift to allow direct ortho-photographs

Affine cameras

Action of projective camera on points and lines projection of point forward projection of line back-projection of line

Action of projective camera on conics and quadrics back-projection to cone projection of quadric

Image of absolute conic

A simple calibration device (i) compute H for each square (corners @ (0, 0), (1, 0), (0, 1), (1, 1)) (ii) compute the imaged circular points H(1, ±i, 0)T (iii) fit a conic to 6 circular points (iv) compute K from w through cholesky factorization (≈ Zhang’s calibration method)

Exercises: Camera calibration

Next class: Single View Metrology Antonio Criminisi

• • A hierarchy of transformations Group of invertible nxn matrices with real elements general linear group on n dimensions. GL(n); Projective linear group: matrices related by a scalar multiplier PL(n); three subgroups: • • Affine group (last row (0, 0, 1)) Euclidean group (upper left 2 x 2 orthogonal) Oriented Euclidean group (upper left 2 x 2 det 1) Alternative, characterize transformation in terms of elements or quantities that are preserved or invariant • e. g. Euclidean transformations (rotation and translation) leave distances unchanged Similarity Affine projective • Similarity: circle imaged as circle; square as square; parallel or perpendicular lines have same relative orientation • Affine: circle becomes ellipse; orthogonal world lines not imaged as orthogonoal; But, parallel lines in the square remain parallel • Projective: parallel world lines imaged as converging lines; tiles closer to camera larger image than those further away.