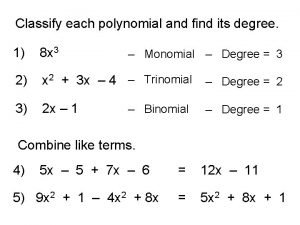QUADRILATERALS OBJECTIVES DEFINE AND CLASSIFY QUADRILATERALS ALONG WITH

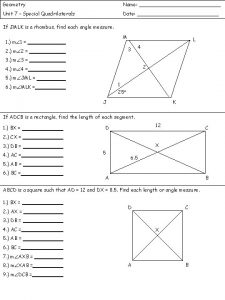
QUADRILATERALS OBJECTIVES: DEFINE AND CLASSIFY QUADRILATERALS ALONG WITH THEIR RELATED PARTS (PARALLELOGRAM, RHOMBUS, RECTANGLE, SQUARE, TRAPEZOID, KITE) Homework: Read pg. 64 -65 pg. 66 # 7 -10, 13(!)

OBJECTIVES To identify any quadrilateral, by name, as specifically as you can, based on its characteristics

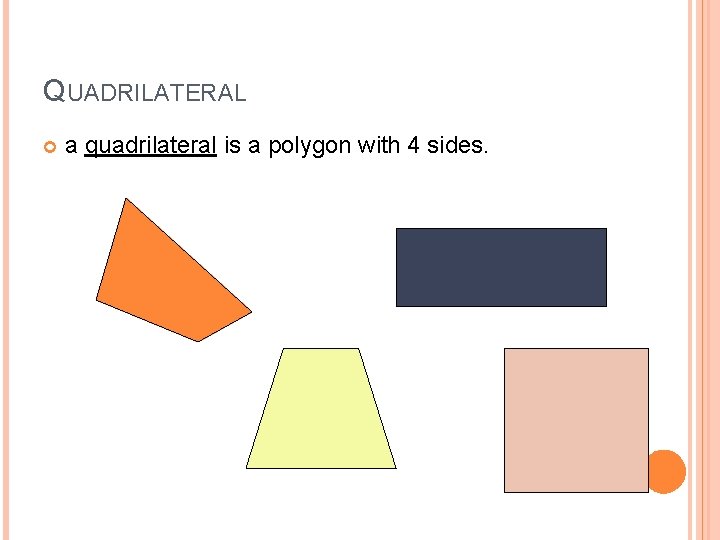
QUADRILATERAL a quadrilateral is a polygon with 4 sides.

SPECIFIC QUADRILATERALS There are several specific types of quadrilaterals. They are classified based on their sides or angles.

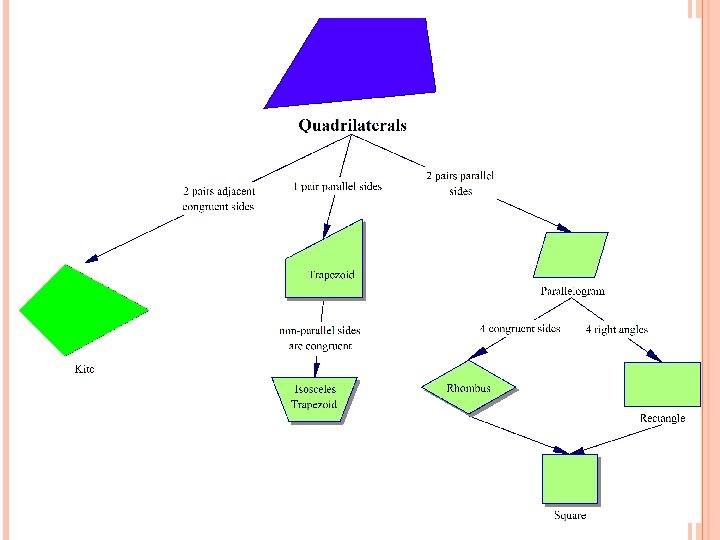
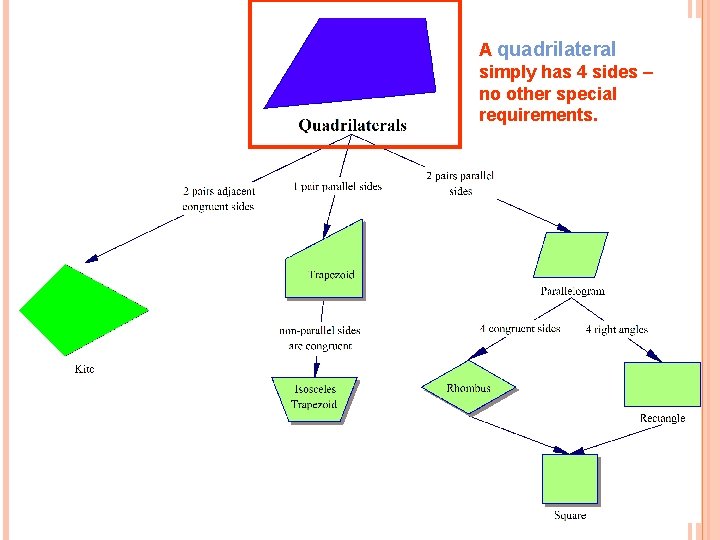
A quadrilateral simply has 4 sides – no other special requirements.

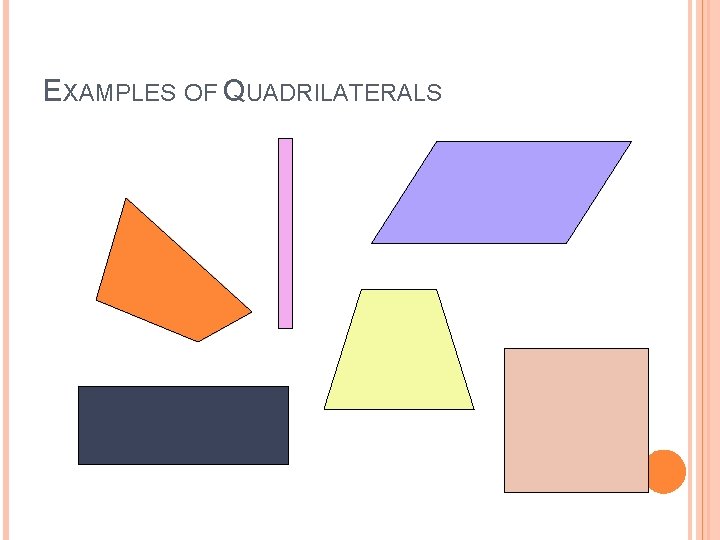
EXAMPLES OF QUADRILATERALS

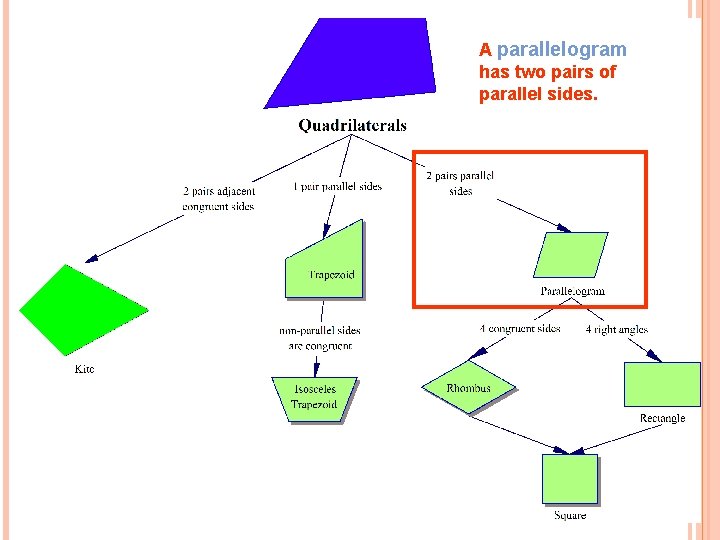
A parallelogram has two pairs of parallel sides.

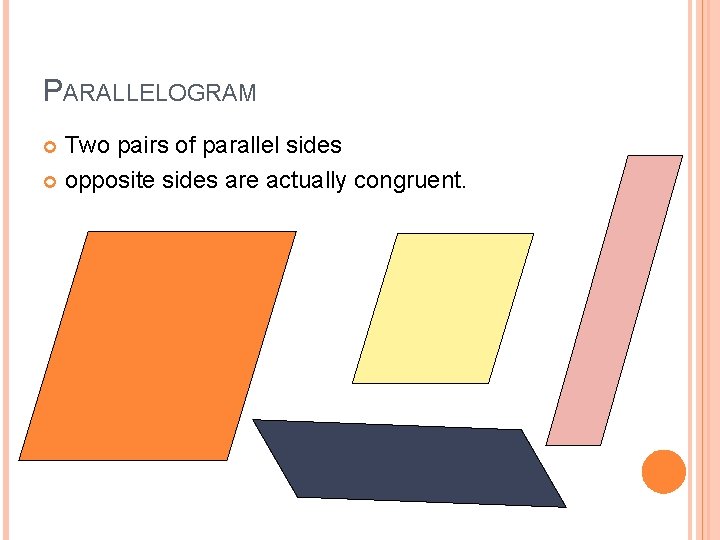
PARALLELOGRAM Two pairs of parallel sides opposite sides are actually congruent.

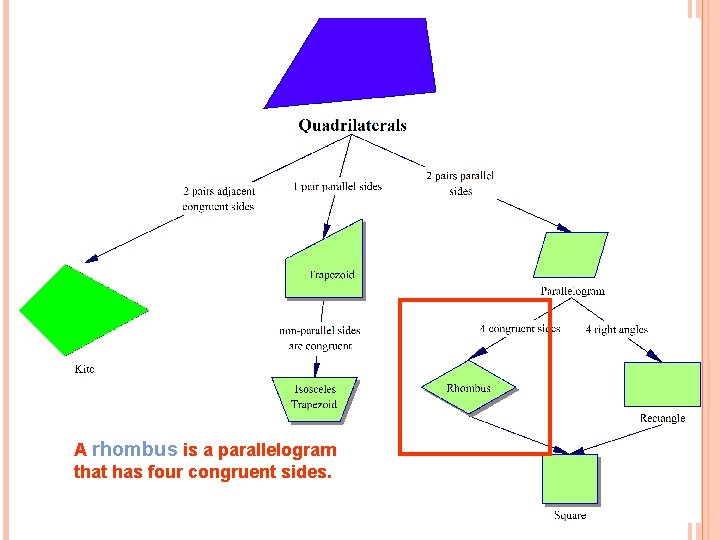
A rhombus is a parallelogram that has four congruent sides.

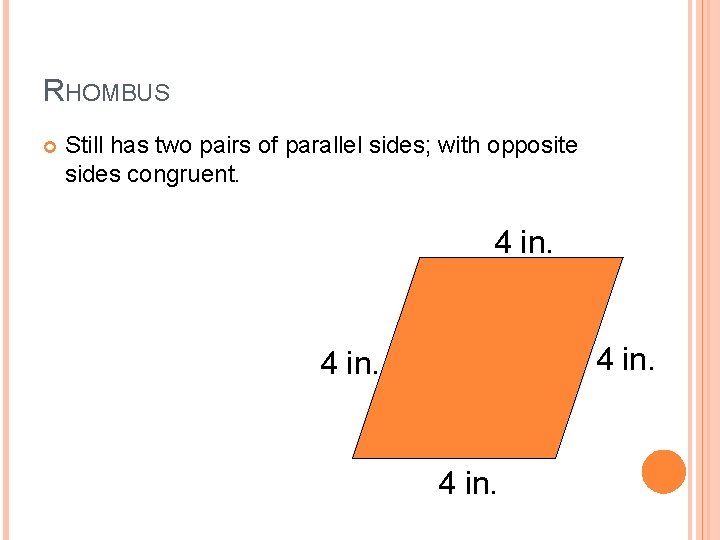
RHOMBUS Still has two pairs of parallel sides; with opposite sides congruent. 4 in.

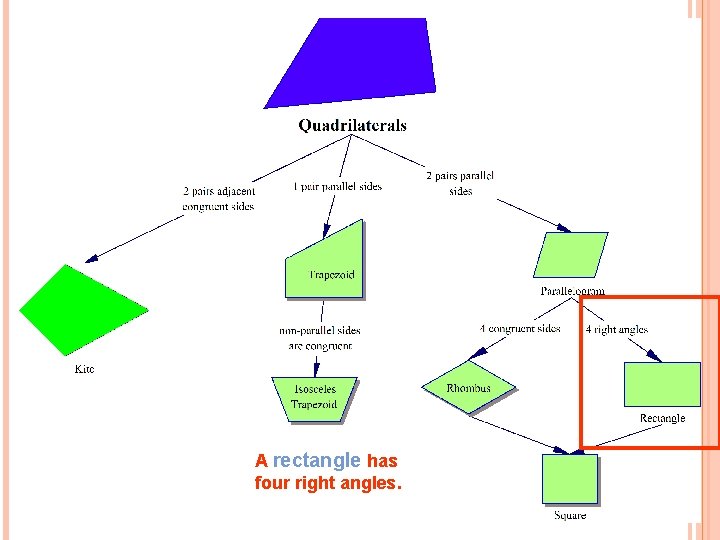
A rectangle has four right angles.

RECTANGLE Still has two pairs of parallel sides; with opposite sides congruent. Has four right angles

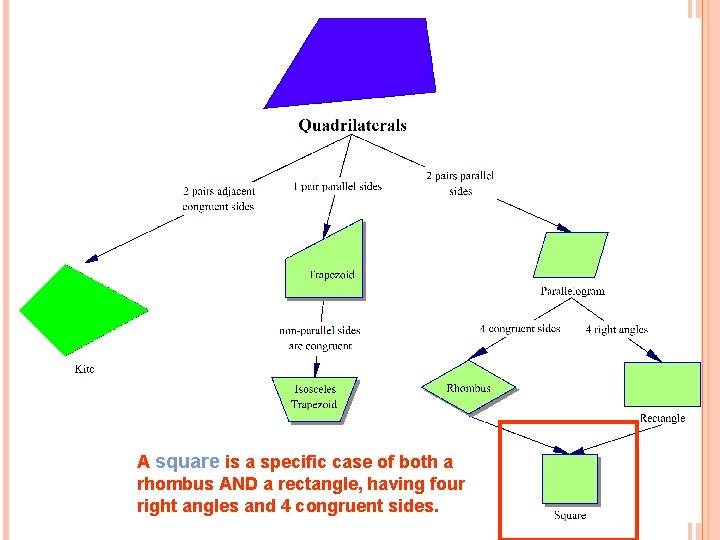
A square is a specific case of both a rhombus AND a rectangle, having four right angles and 4 congruent sides.

SQUARE Still has two pairs of parallel sides. Has four congruent sides Has four right angles

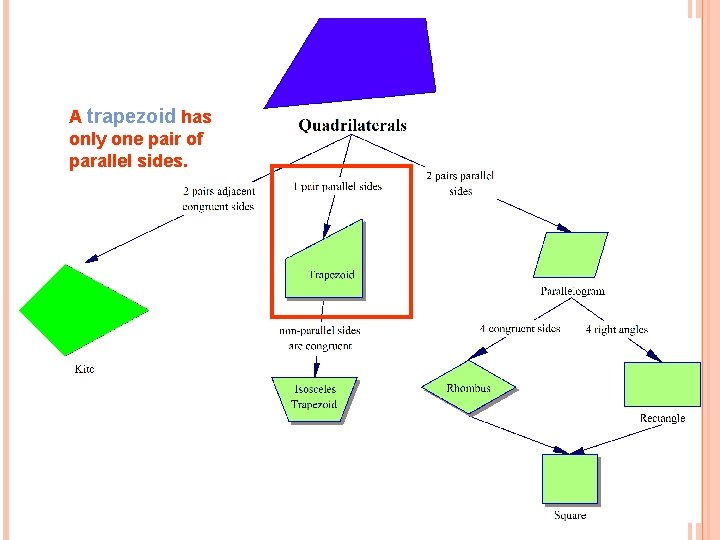
A trapezoid has only one pair of parallel sides.

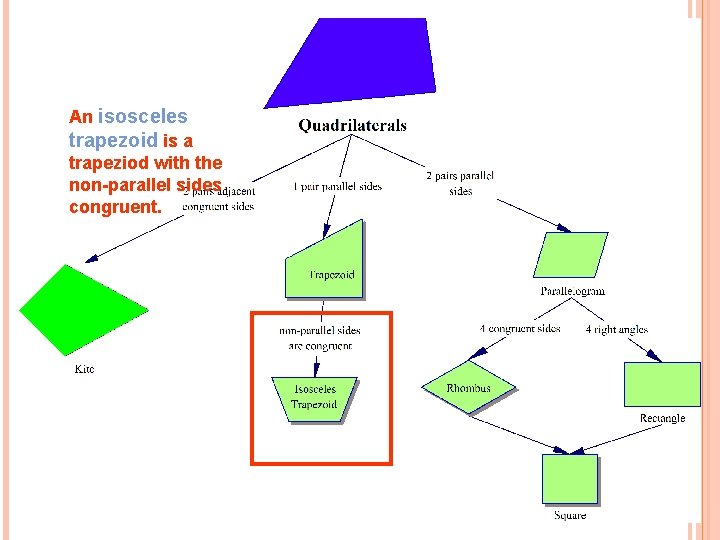
An isosceles trapezoid is a trapeziod with the non-parallel sides congruent.

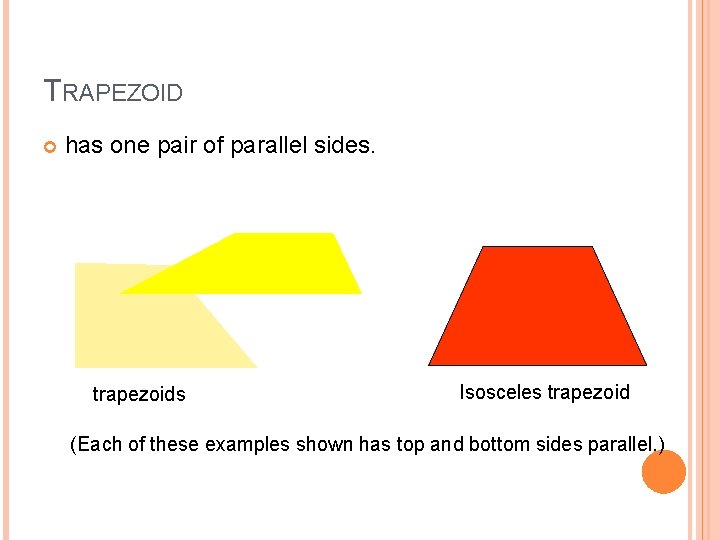
TRAPEZOID has one pair of parallel sides. trapezoids Isosceles trapezoid (Each of these examples shown has top and bottom sides parallel. )

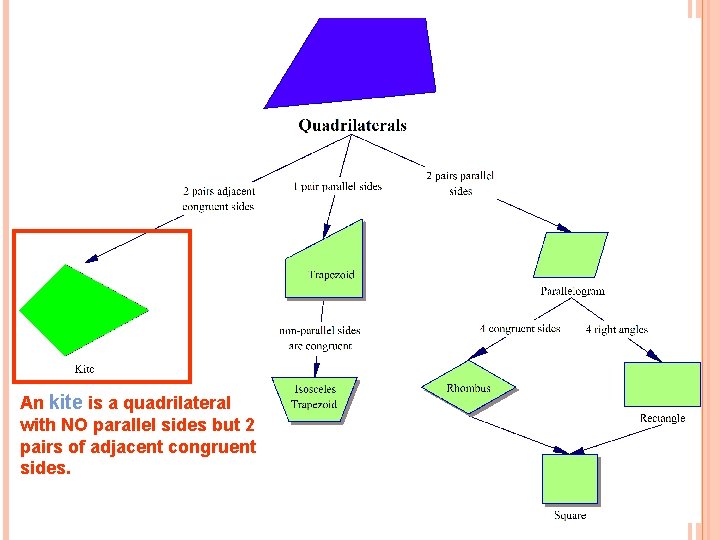
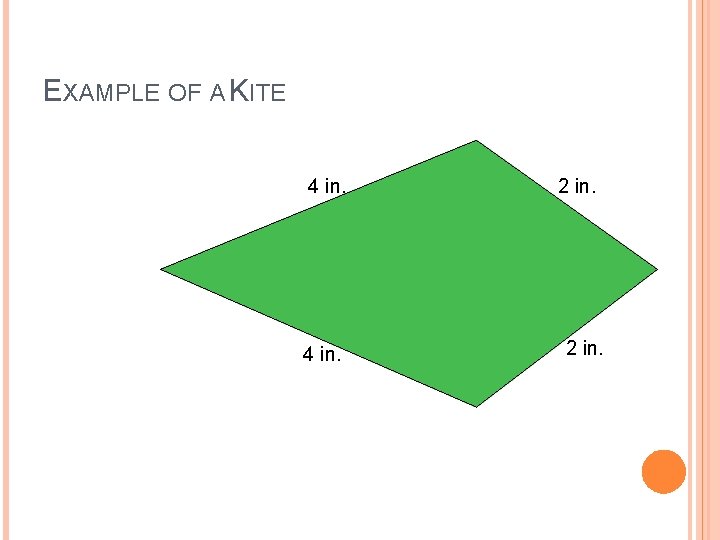
An kite is a quadrilateral with NO parallel sides but 2 pairs of adjacent congruent sides.

EXAMPLE OF A KITE 4 in. 2 in.

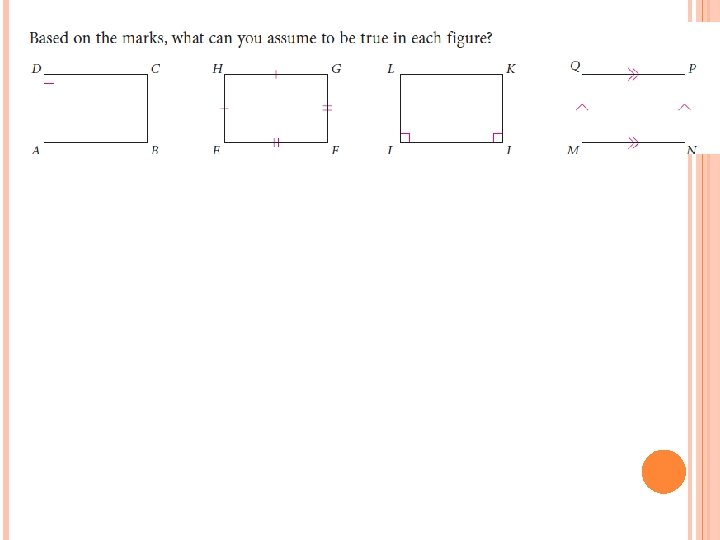
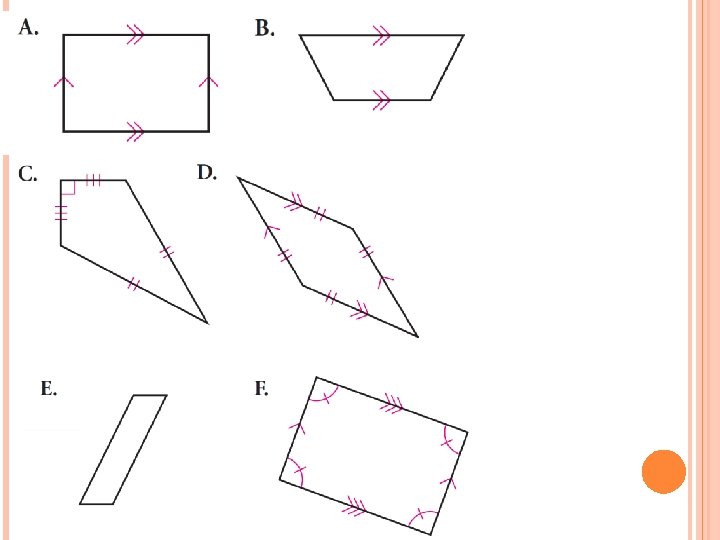
CARNEGIE Homework: Read pg. 64 -65 pg. 66 # 7 -10, 13(!)

TRAPEZOIDS AND KITES Chapter 5. 3 Homework: pg. 272 # 5, 6, 8, 9

ESSENTIAL QUESTIONS How do I use properties of trapezoids? How do I use properties of kites?

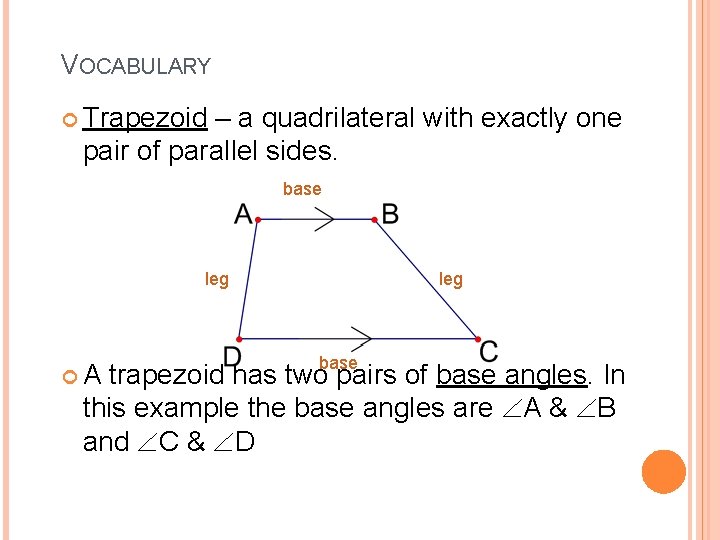
VOCABULARY Trapezoid – a quadrilateral with exactly one pair of parallel sides. base leg base A trapezoid has two pairs of base angles. In this example the base angles are A & B and C & D

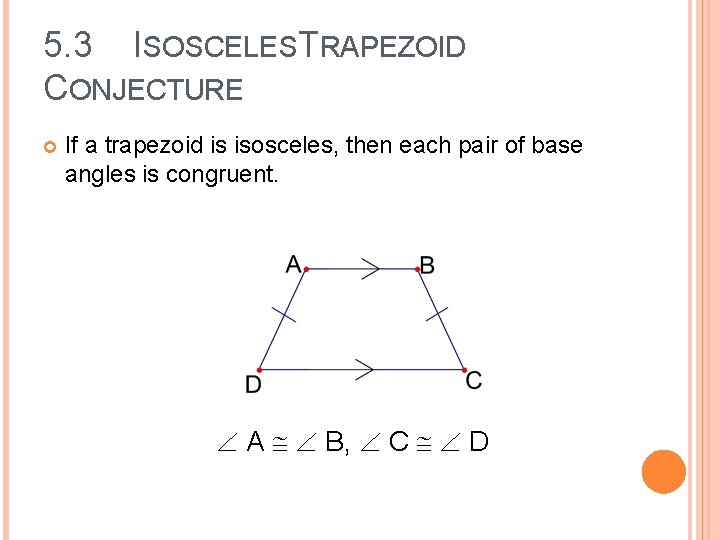
5. 3 ISOSCELESTRAPEZOID CONJECTURE If a trapezoid is isosceles, then each pair of base angles is congruent. A B, C D

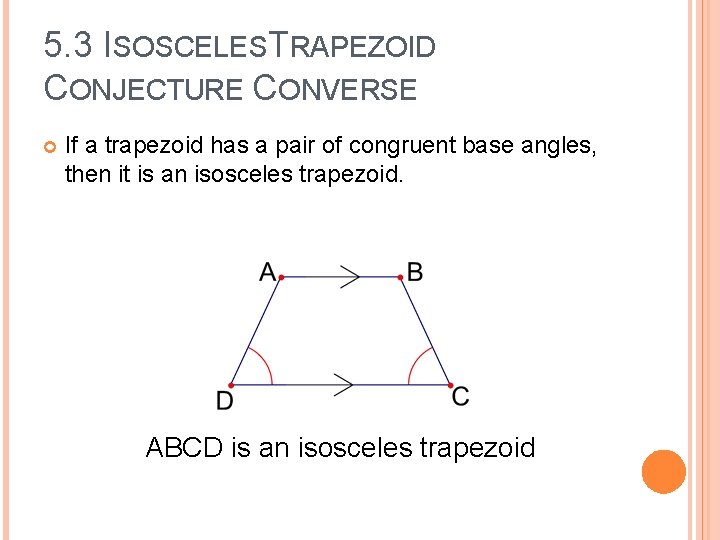
5. 3 ISOSCELESTRAPEZOID CONJECTURE CONVERSE If a trapezoid has a pair of congruent base angles, then it is an isosceles trapezoid. ABCD is an isosceles trapezoid

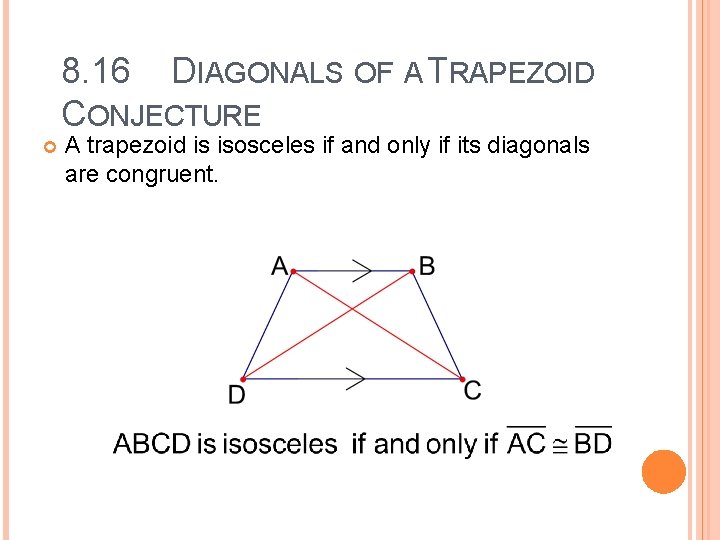
8. 16 DIAGONALS OF A TRAPEZOID CONJECTURE A trapezoid is isosceles if and only if its diagonals are congruent.

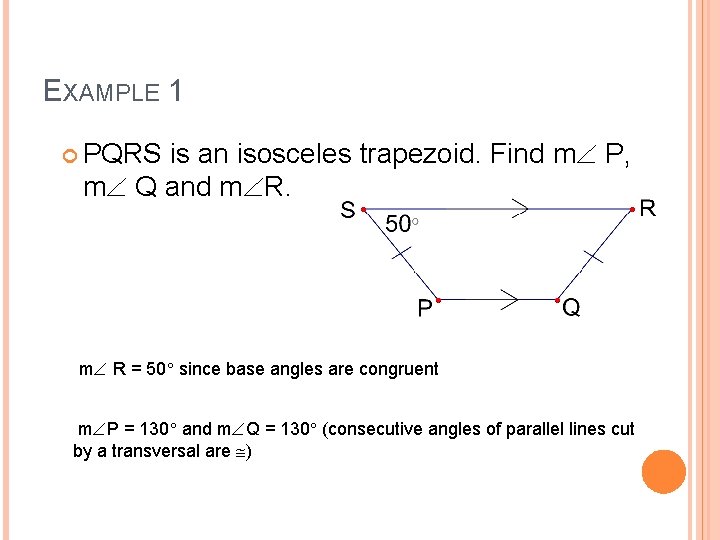
EXAMPLE 1 PQRS is an isosceles trapezoid. Find m P, m Q and m R = 50 since base angles are congruent m P = 130 and m Q = 130 (consecutive angles of parallel lines cut by a transversal are )

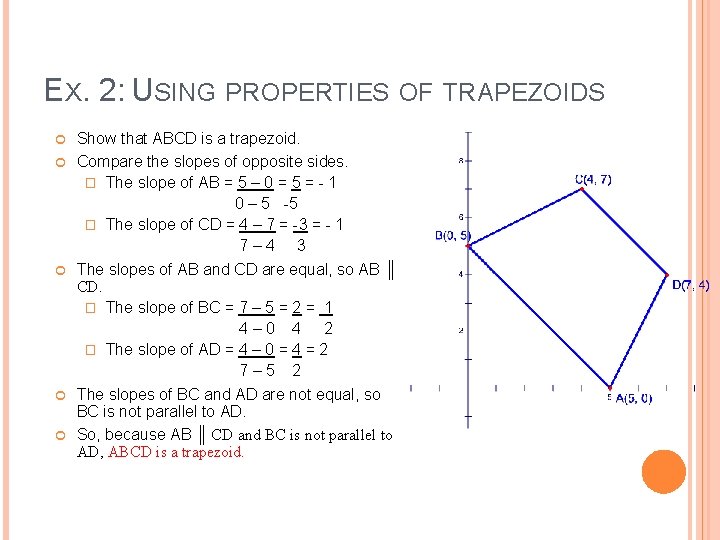
EX. 2: USING PROPERTIES OF TRAPEZOIDS Show that ABCD is a trapezoid. Compare the slopes of opposite sides. � The slope of AB = 5 – 0 = 5 = - 1 0 – 5 -5 � The slope of CD = 4 – 7 = -3 = - 1 7 – 4 3 The slopes of AB and CD are equal, so AB ║ CD. � The slope of BC = 7 – 5 = 2 = 1 4 – 0 4 2 � The slope of AD = 4 – 0 = 4 = 2 7 – 5 2 The slopes of BC and AD are not equal, so BC is not parallel to AD. So, because AB ║ CD and BC is not parallel to AD, ABCD is a trapezoid.

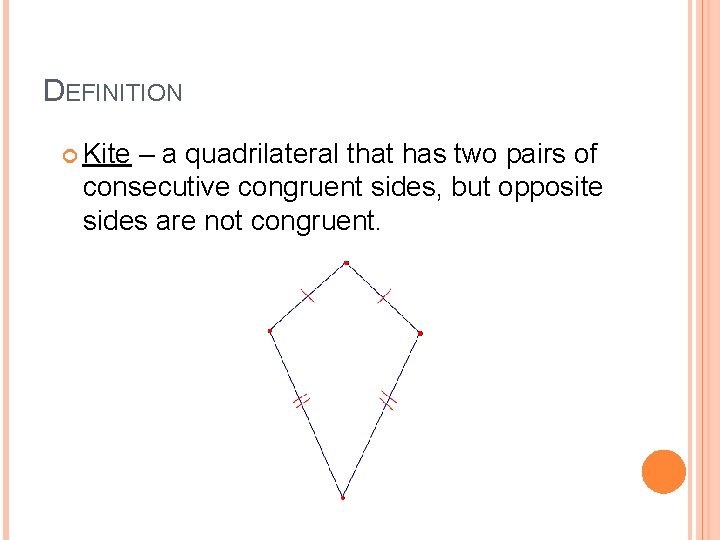
DEFINITION Kite – a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.

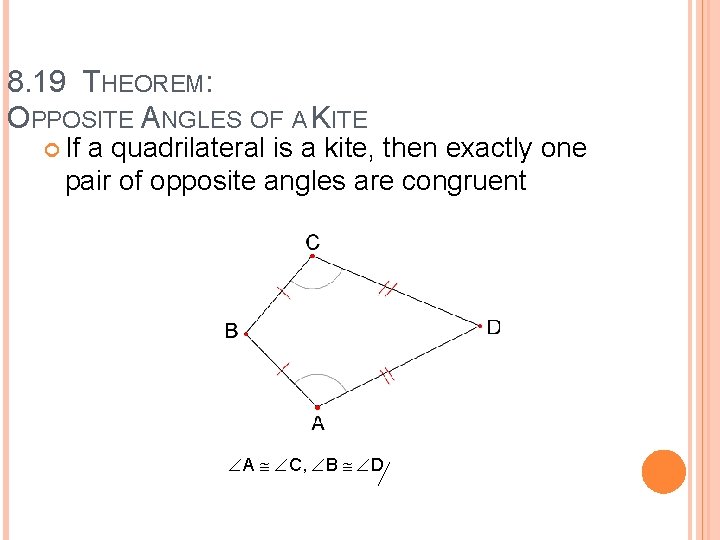
8. 19 THEOREM: OPPOSITE ANGLES OF A KITE If a quadrilateral is a kite, then exactly one pair of opposite angles are congruent A C, B D

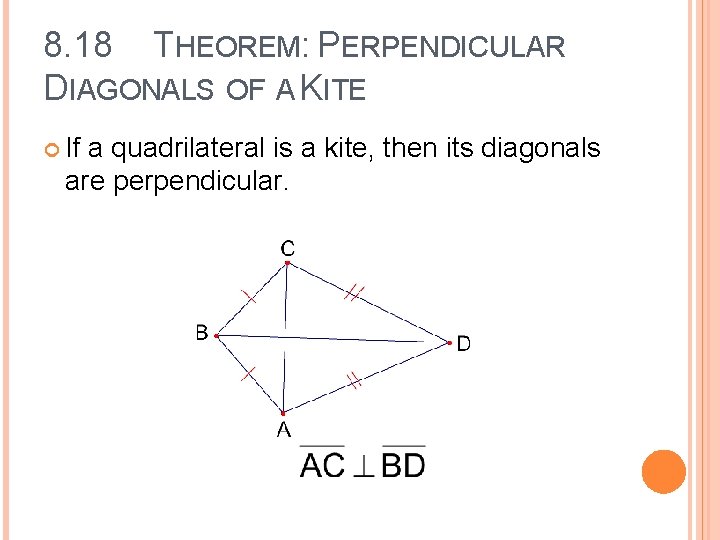
8. 18 THEOREM: PERPENDICULAR DIAGONALS OF A KITE If a quadrilateral is a kite, then its diagonals are perpendicular.

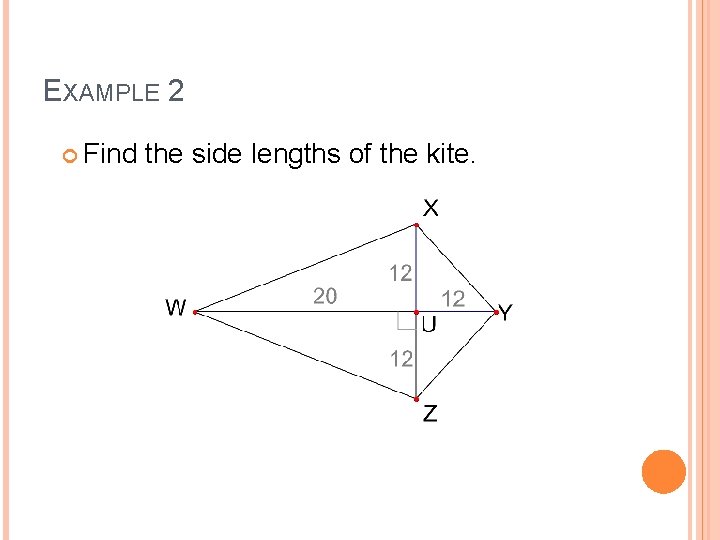
EXAMPLE 2 Find the side lengths of the kite.

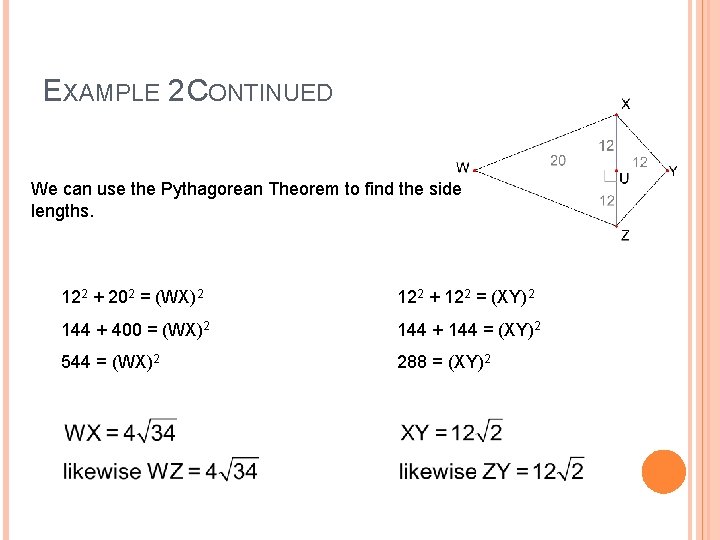
EXAMPLE 2 CONTINUED We can use the Pythagorean Theorem to find the side lengths. 122 + 202 = (WX)2 122 + 122 = (XY)2 144 + 400 = (WX)2 144 + 144 = (XY)2 544 = (WX)2 288 = (XY)2

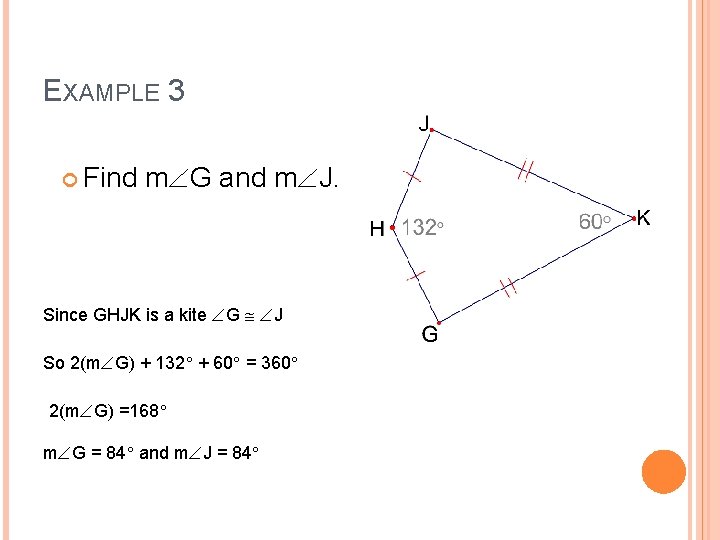
EXAMPLE 3 Find m G and m J. Since GHJK is a kite G J So 2(m G) + 132 + 60 = 360 2(m G) =168 m G = 84 and m J = 84

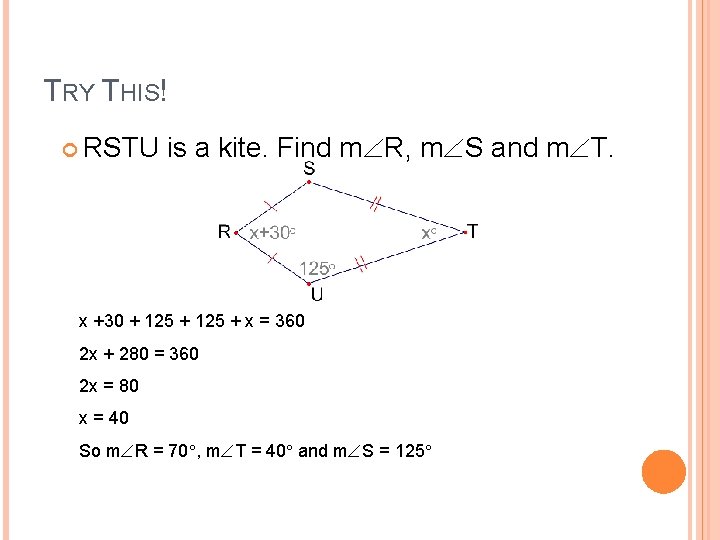
TRY THIS! RSTU is a kite. Find m R, m S and m T. x +30 + 125 + x = 360 2 x + 280 = 360 2 x = 80 x = 40 So m R = 70 , m T = 40 and m S = 125

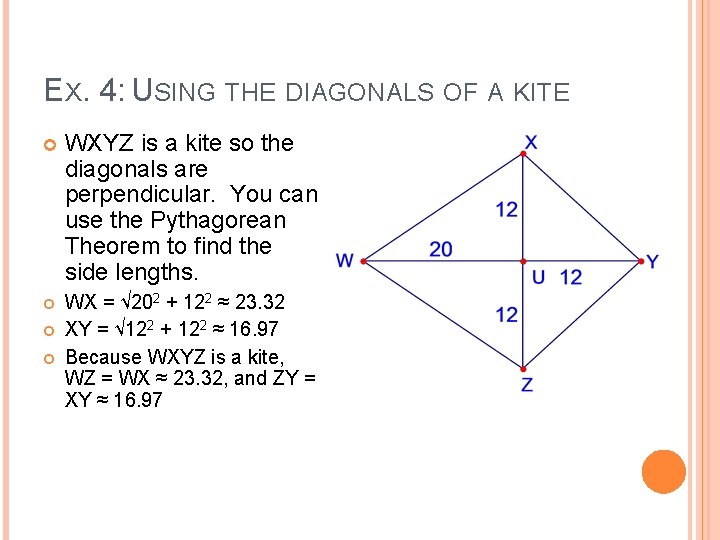
EX. 4: USING THE DIAGONALS OF A KITE WXYZ is a kite so the diagonals are perpendicular. You can use the Pythagorean Theorem to find the side lengths. WX = √ 202 + 122 ≈ 23. 32 XY = √ 122 + 122 ≈ 16. 97 Because WXYZ is a kite, WZ = WX ≈ 23. 32, and ZY = XY ≈ 16. 97

EX. 5: ANGLES OF A KITE Find m G and m J in the diagram at the 132° 60° right. SOLUTION: GHJK is a kite, so G ≅ J and m G = m J. 2(m G) + 132° + 60° = 360°Sum of measures of int. s of a quad. is 360° 2(m G) = 168°Simplify m G = 84° Divide each side by 2. So, m J = m G = 84°

5. 4 PROPERTIES OF MIDSEGMENTS DEFINE AND DISCOVER PROPERTIES OF MIDSEGMENTS IN TRIANGLES AND TRAPEZOIDS HOMEWORK Go over class notes, solve pg. 278 # 5, 6, 7

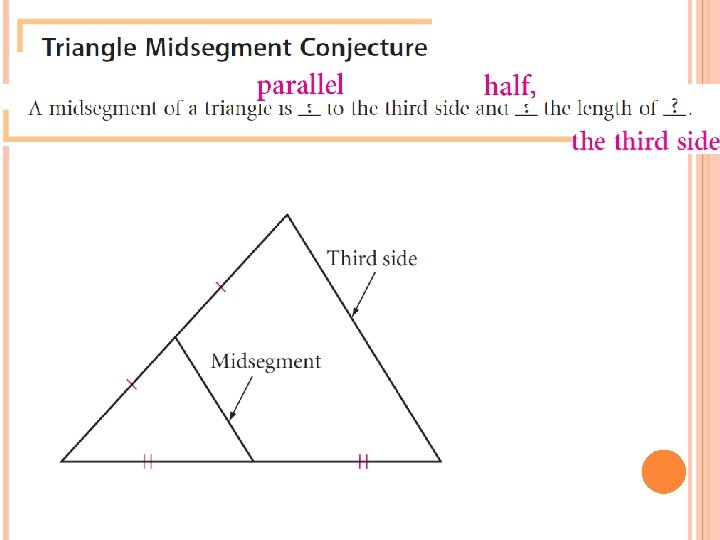
HOMEWORK

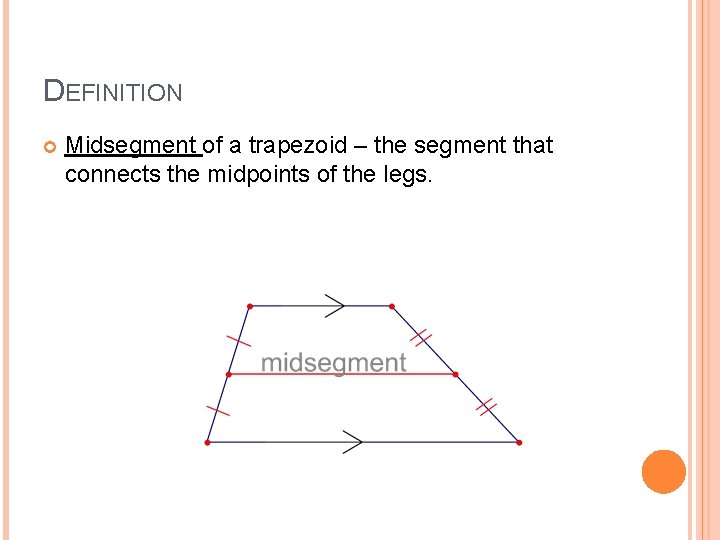
DEFINITION Midsegment of a trapezoid – the segment that connects the midpoints of the legs.

MIDSEGMENT THEOREM FOR TRAPEZOIDS The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases.

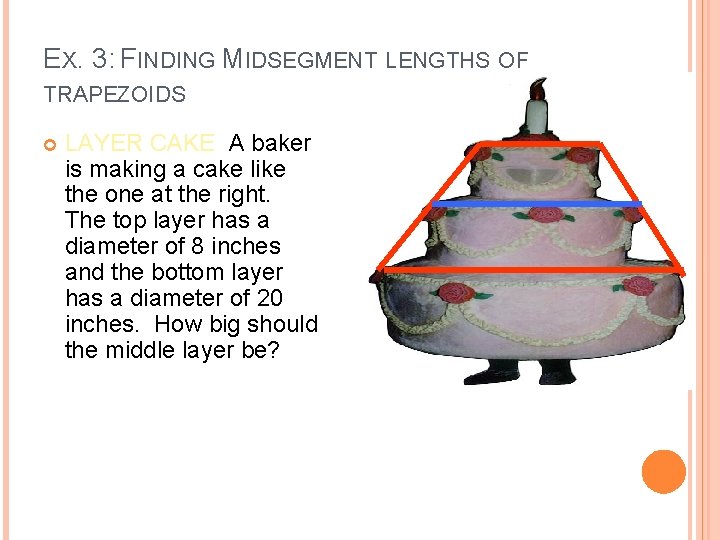
EX. 3: FINDING MIDSEGMENT LENGTHS OF TRAPEZOIDS LAYER CAKE A baker is making a cake like the one at the right. The top layer has a diameter of 8 inches and the bottom layer has a diameter of 20 inches. How big should the middle layer be?

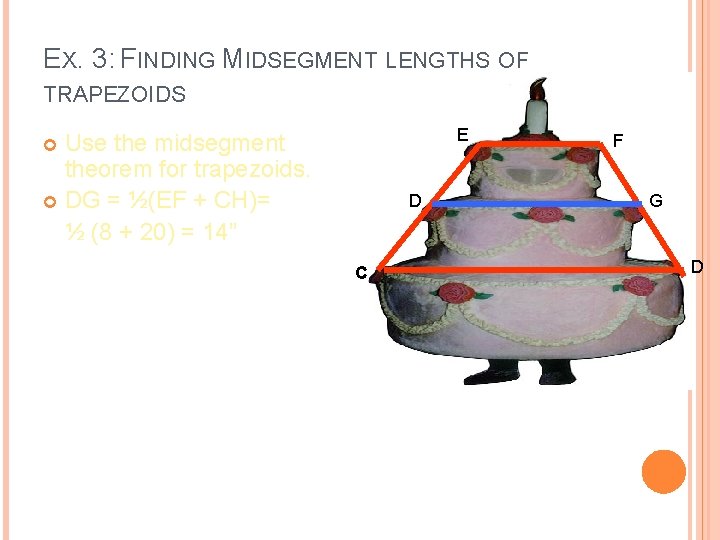
EX. 3: FINDING MIDSEGMENT LENGTHS OF TRAPEZOIDS E Use the midsegment theorem for trapezoids. DG = ½(EF + CH)= ½ (8 + 20) = 14” D C F G D