Rational and Irrational Numbers Classifying Numbers Numbers can

Rational and Irrational Numbers

Classifying Numbers • Numbers can be classified • For instance, we can pick out all of the numbers that are divisible by 2. They are classified as even numbers. • We can also classify numbers in other ways.

Rational and Irrational • Numbers can be classified as rational numbers. • Rational numbers are numbers that in decimal form, are either terminating OR repeating.

Terminating numbers • A terminating number is a number that terminates, which means ends. • Examples of terminating numbers: 3. 14 4. 5678932221 0. 33339 • Examples of numbers that do NOT terminate (do not end) 3. 333333… pi 0. 121231234….

Repeating Numbers • A repeating number is a number that does not terminate, but it repeats over and over EXACTLY THE SAME WAY • Examples of repeating numbers: 3. 33333…. 4. 3434…… Examples of NON-repeating numbers: 3. 343453456…. . pi 9. 352109….

Rational vs. Irrational • If a number repeats exactly, or terminates, then it is a rational number. • If a real number is NOT rational, then it is irrational.

Rational or irrational? 1 rational irrational 6. 2533678 irrational

Real Numbers • Another classification of numbers is the set of numbers called Real Numbers. • This one is easy. Real numbers are the rational numbers and the irrational numbers combined. • Real = Rational + Irrational

• Place the following numbers in order from least to greatest. -7, 14/3, 280%, 1 3/7 Step 1. Change into decimals. Step 2. Place on a number line.

-7 = -7. 0 14/3 = 14 divided by 3 4. 7 280% = 280 divided by 100 2. 8 1 3/7 = 1 + 3/7 1. 43 -7 1 3/7 280% 14/3 0 Order from least to greatest: -7, 1 3/7, 280%, 14/3

Do Example 1 Now Example 1 Order numbers from least to greatest; place on number line: 5/6 4 ¼ 300% 0. 23 3/10 Step 1: Convert to decimals: 5/6 = ______ 4 ¼ = ______ 300% = ______ 0. 23 = ______ 3/10 = ______

Example 1 Step 1: Convert to decimals: 5/6 = 0. 833 4 ¼ = 4. 25 300% = 3. 0 0. 23 = 0. 23 3/10 = 0. 3 Order from least to greatest: 0. 23, 0. 833, 3. 0, 4. 25

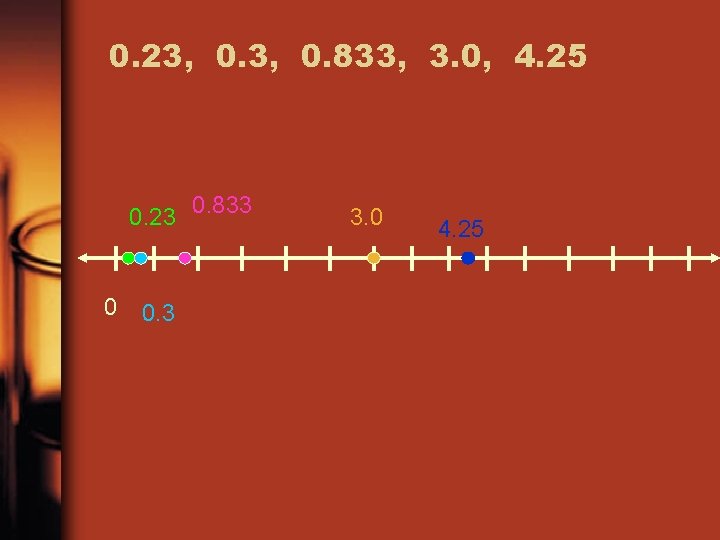
0. 23, 0. 833, 3. 0, 4. 25 0. 23 0 0. 3 0. 833 3. 0 4. 25

Example 2 • Which is smaller: -2 or -3 • -3 is smaller • Convert -3 ½ to decimal form • -3 + - ½ = -3 + -0. 5 = -3. 5