Chapter 6 Quadrilaterals Section 6 1 Polygons Polygon

Chapter 6 Quadrilaterals

Section 6. 1 Polygons

Polygon • A polygon is formed by three or more segments called sides – No two sides with a common endpoint are collinear. – Each side intersects exactly two other sides, one at each endpoint. – Each endpoint of a side is a vertex of the polygon. – Polygons are named by listing the vertices consecutively.

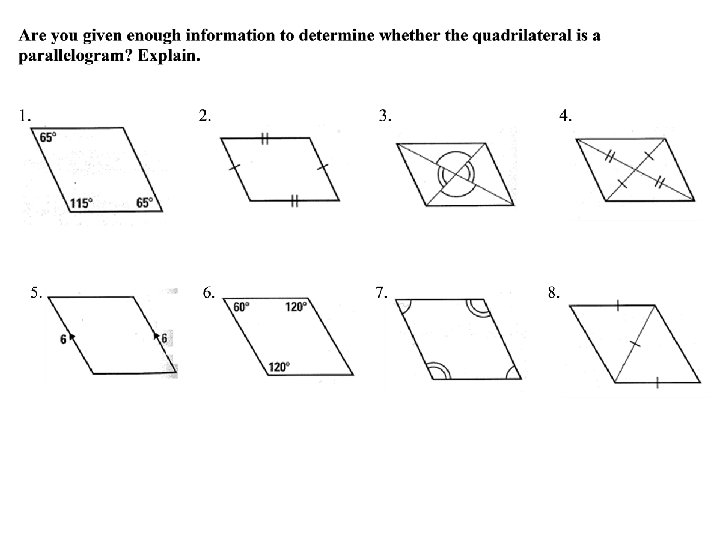
Identifying polygons • State whether the figure is a polygon. If not, explain why.

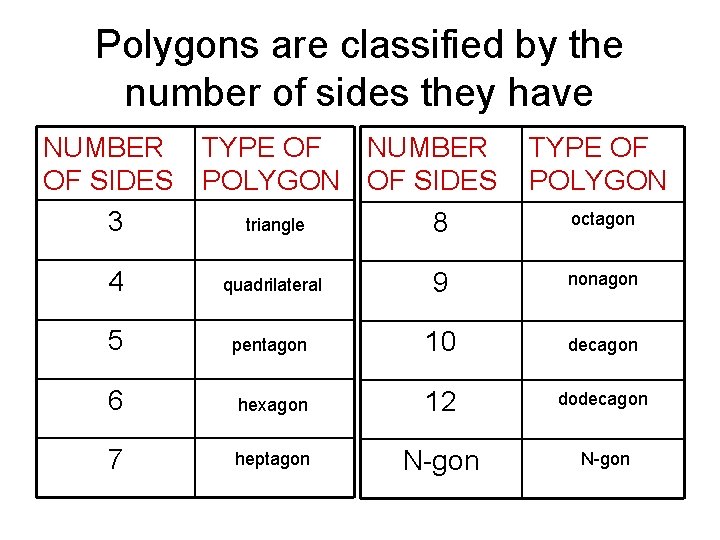
Polygons are classified by the number of sides they have NUMBER OF SIDES 3 TYPE OF NUMBER POLYGON OF SIDES TYPE OF POLYGON triangle 8 octagon 4 quadrilateral 9 nonagon 5 pentagon 10 decagon 6 hexagon 12 dodecagon 7 heptagon N-gon

Two Types of Polygons: 1. Convex: If a line was extended from the sides of a polygon, it will NOT go through the interior of the polygon. Example:

2. Concave: If a line was extended from the sides of a polygon, it WILL go through the interior of the polygon. Example:

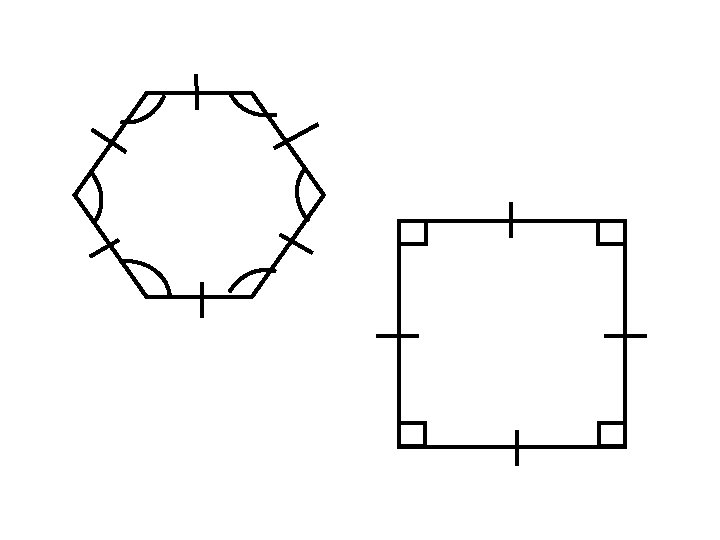
Regular Polygon • A polygon is regular if it is equilateral and equiangular • A polygon is equilateral if all of its sides are congruent • A polygon is equiangular if all of its interior angles are congruent

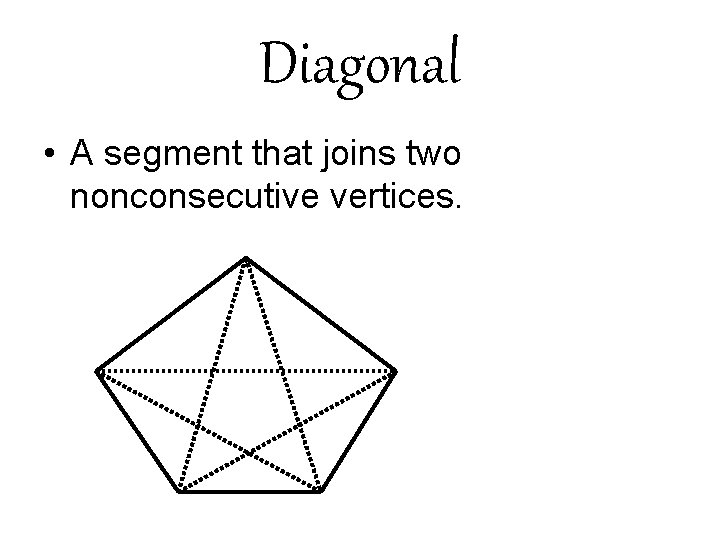
Diagonal • A segment that joins two nonconsecutive vertices.

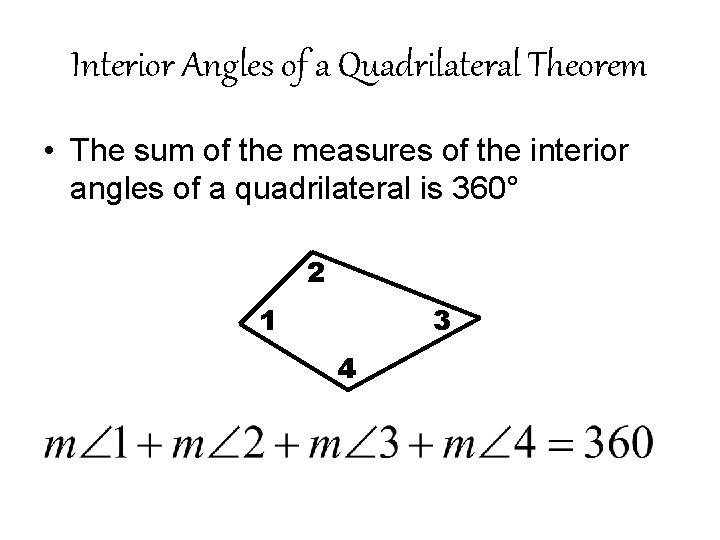
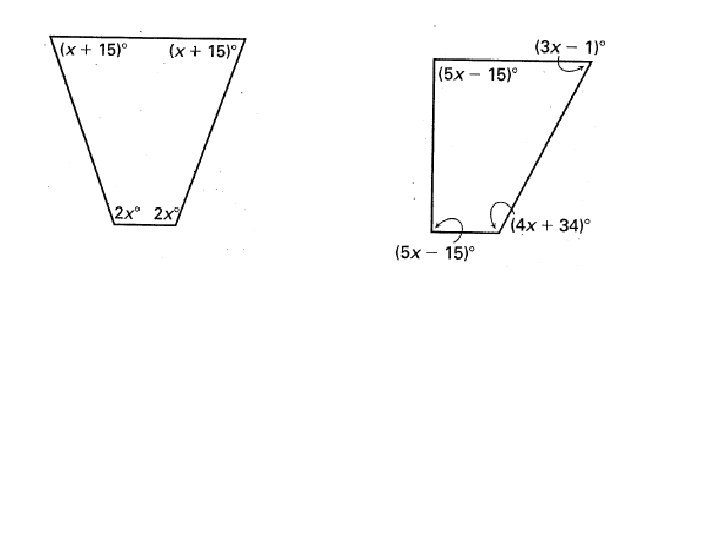
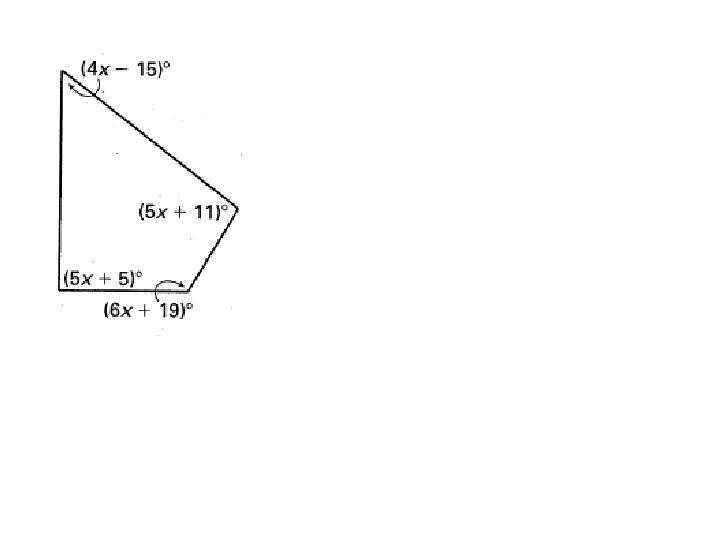
Interior Angles of a Quadrilateral Theorem • The sum of the measures of the interior angles of a quadrilateral is 360° 2 1 3 4

Section 6. 2 Properties of Parallelograms

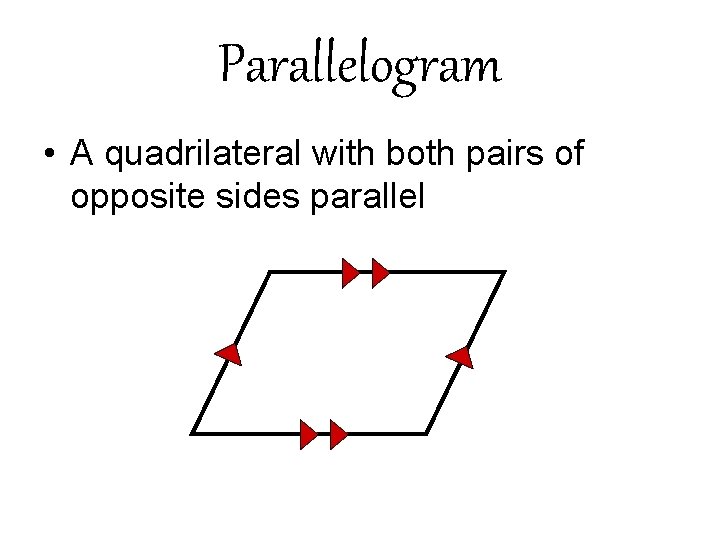
Parallelogram • A quadrilateral with both pairs of opposite sides parallel

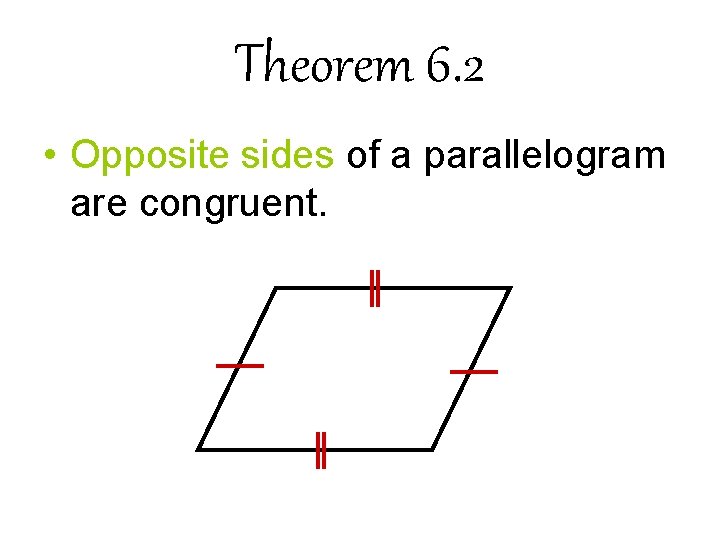
Theorem 6. 2 • Opposite sides of a parallelogram are congruent.

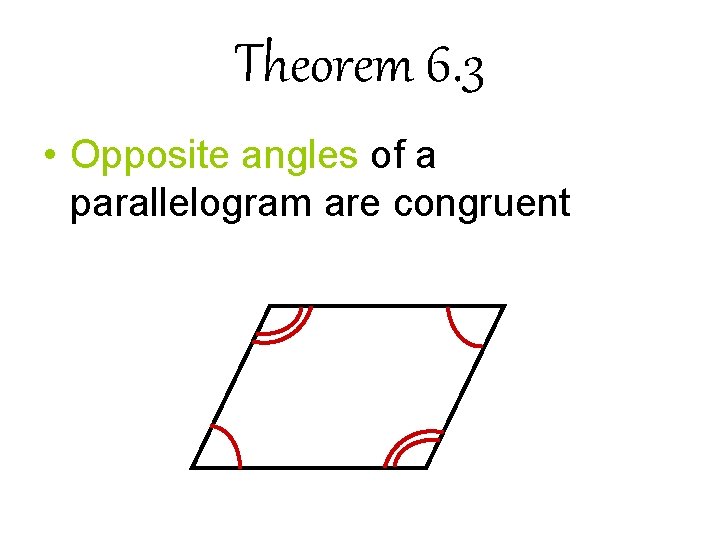
Theorem 6. 3 • Opposite angles of a parallelogram are congruent

Theorem 6. 4 • Consecutive angles of a parallelogram are supplementary. 2 1 3 4

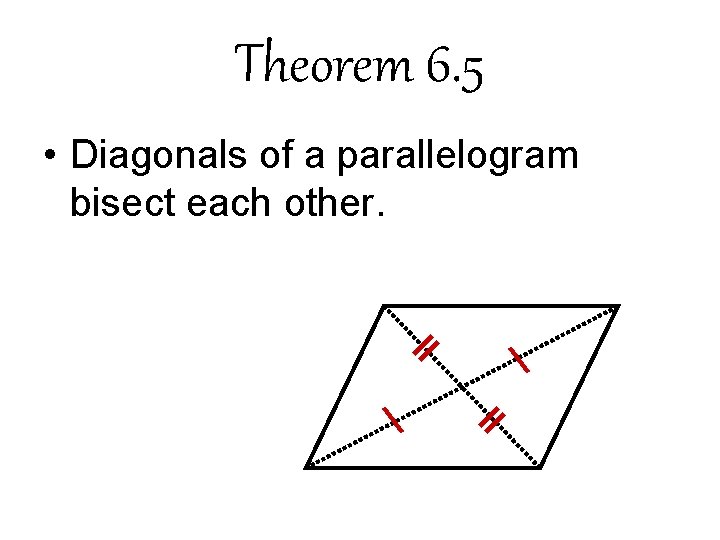
Theorem 6. 5 • Diagonals of a parallelogram bisect each other.

Section 6. 3 Proving Quadrilaterals are Parallelograms

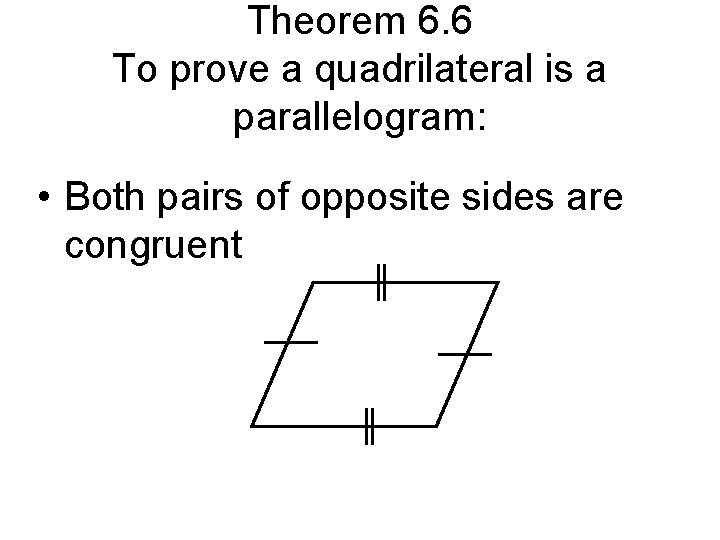
Theorem 6. 6 To prove a quadrilateral is a parallelogram: • Both pairs of opposite sides are congruent

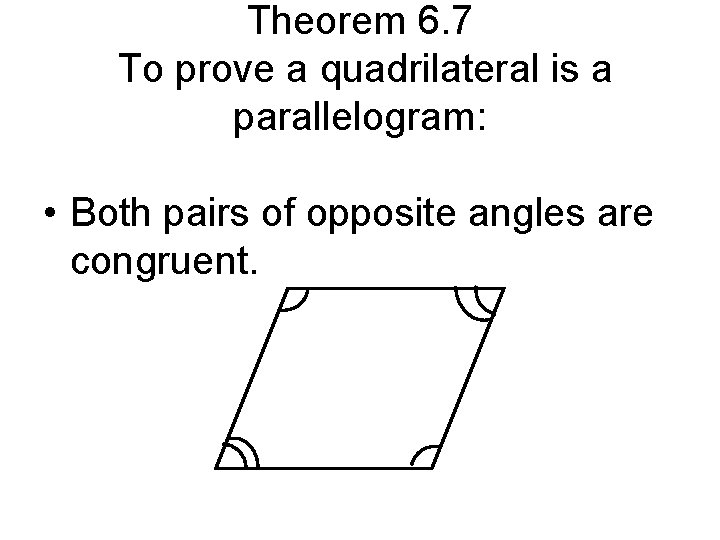
Theorem 6. 7 To prove a quadrilateral is a parallelogram: • Both pairs of opposite angles are congruent.

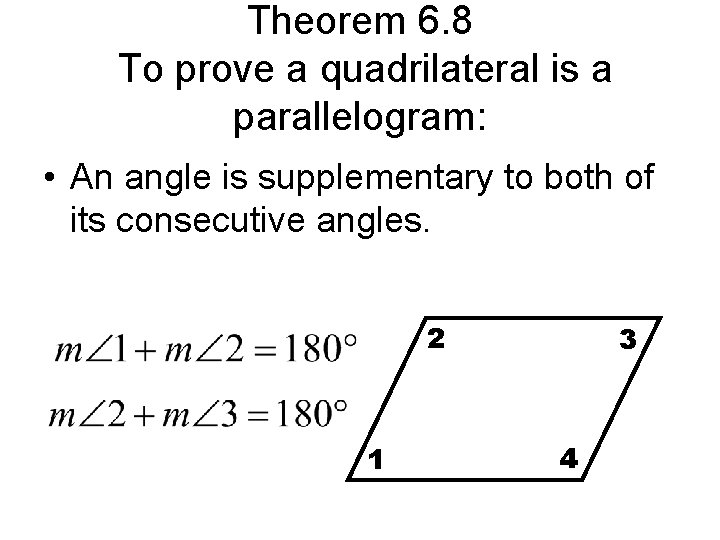
Theorem 6. 8 To prove a quadrilateral is a parallelogram: • An angle is supplementary to both of its consecutive angles. 2 1 3 4

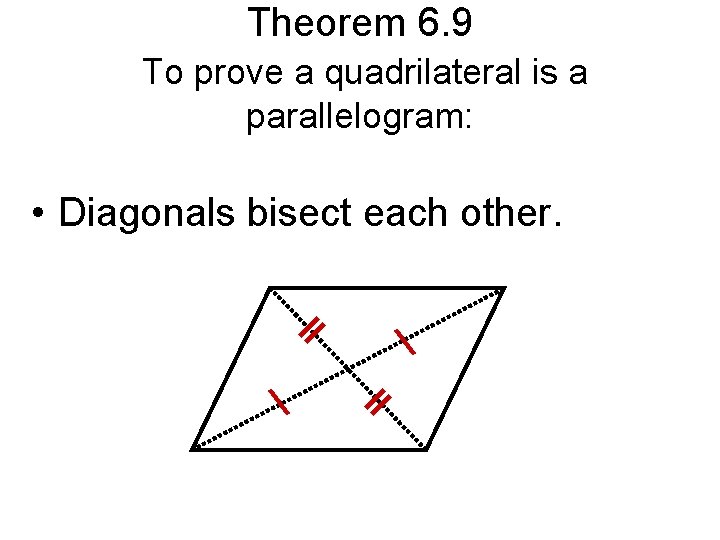
Theorem 6. 9 To prove a quadrilateral is a parallelogram: • Diagonals bisect each other.

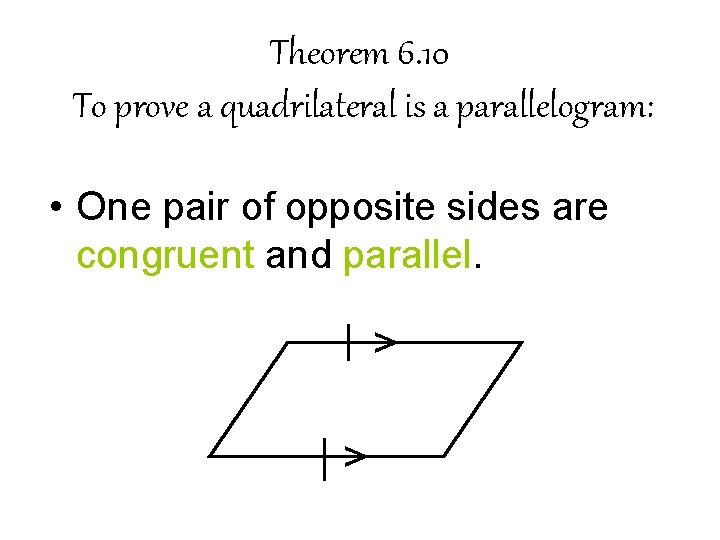
Theorem 6. 10 To prove a quadrilateral is a parallelogram: • One pair of opposite sides are congruent and parallel. > >

Section 6. 4 Types of parallelograms

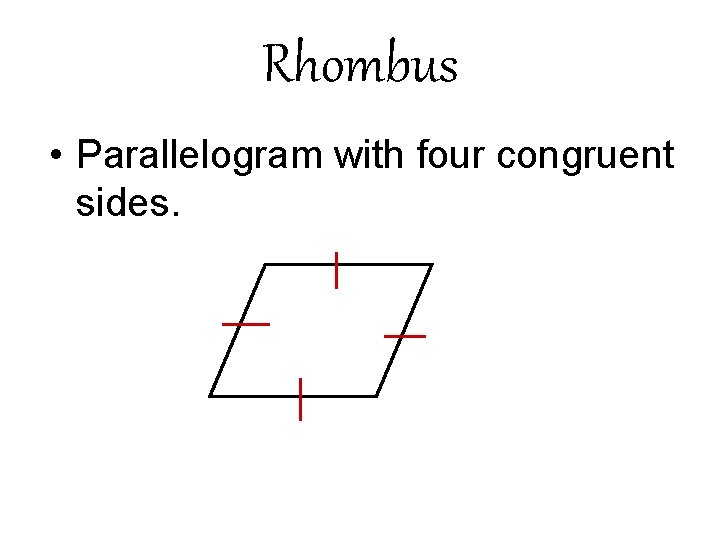
Rhombus • Parallelogram with four congruent sides.

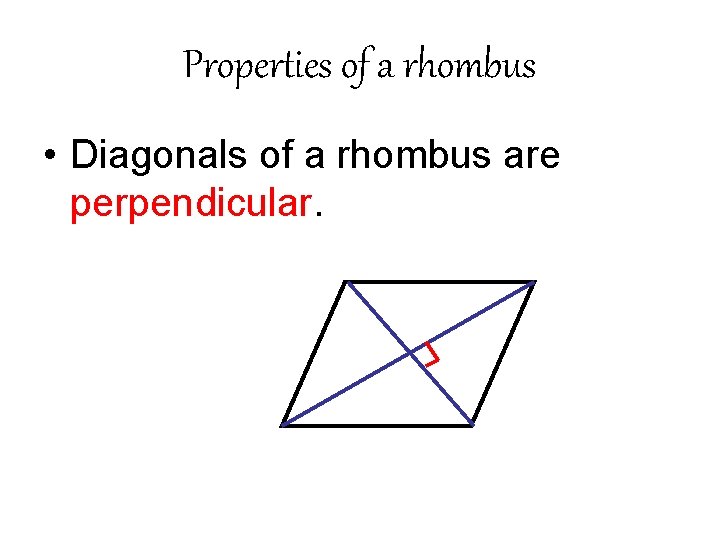
Properties of a rhombus • Diagonals of a rhombus are perpendicular.

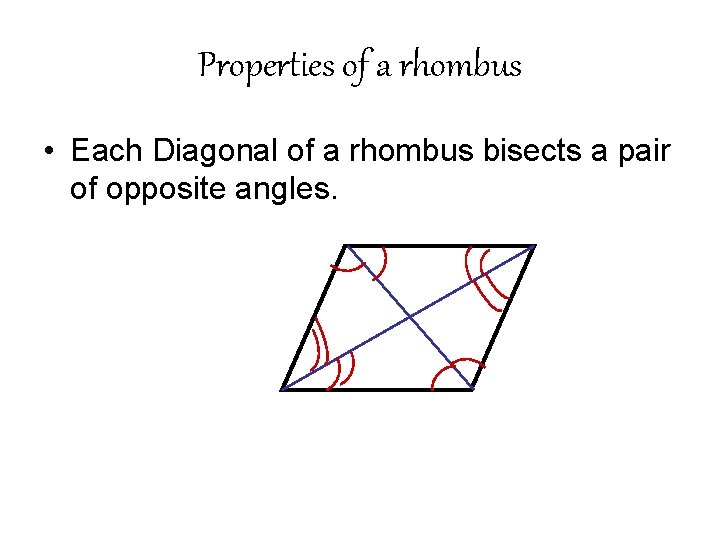
Properties of a rhombus • Each Diagonal of a rhombus bisects a pair of opposite angles.

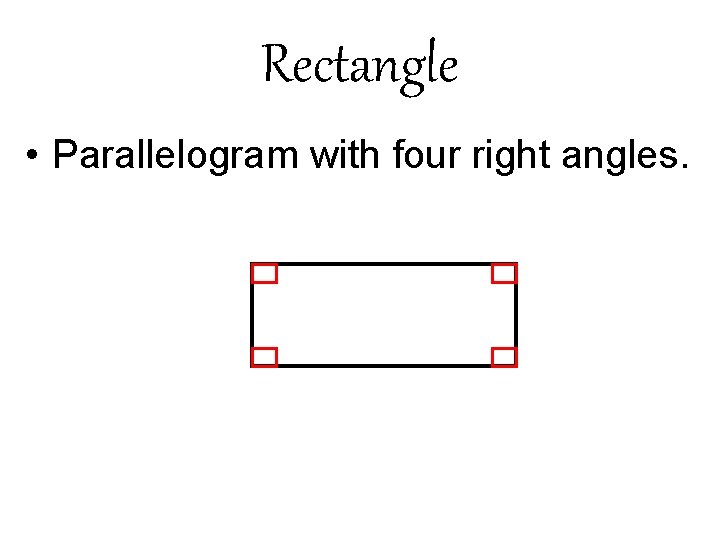
Rectangle • Parallelogram with four right angles.

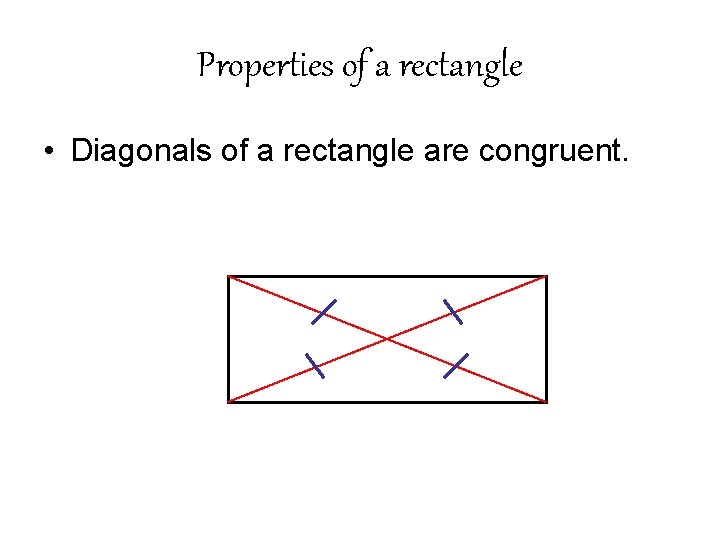
Properties of a rectangle • Diagonals of a rectangle are congruent.

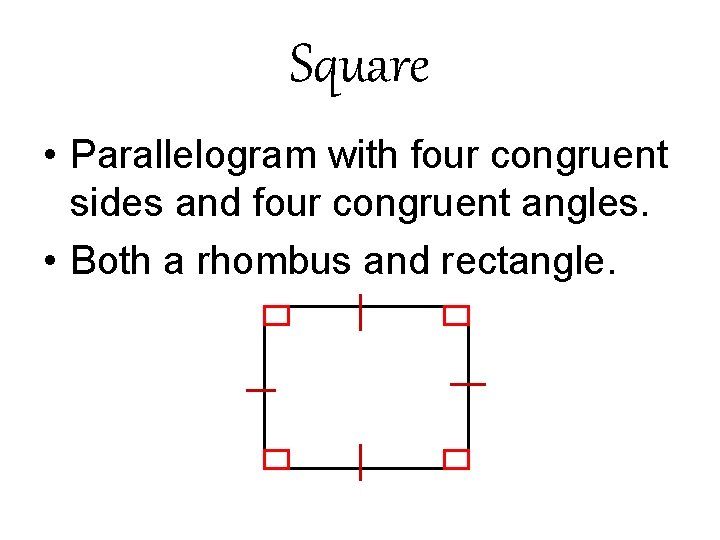
Square • Parallelogram with four congruent sides and four congruent angles. • Both a rhombus and rectangle.

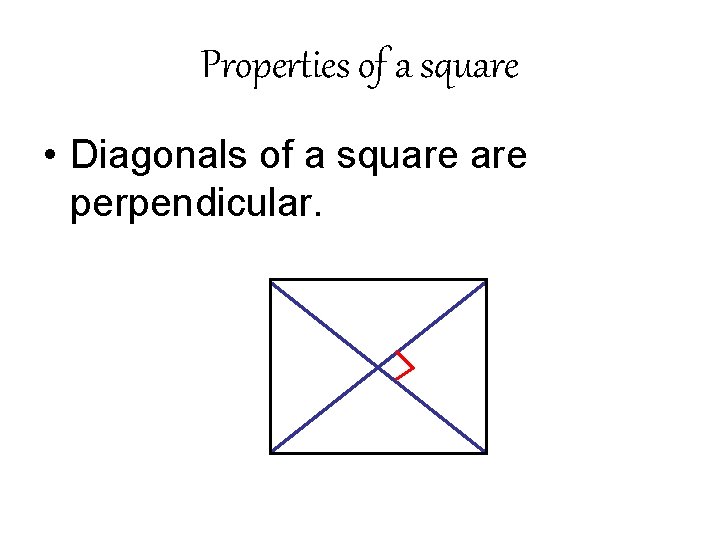
Properties of a square • Diagonals of a square perpendicular.

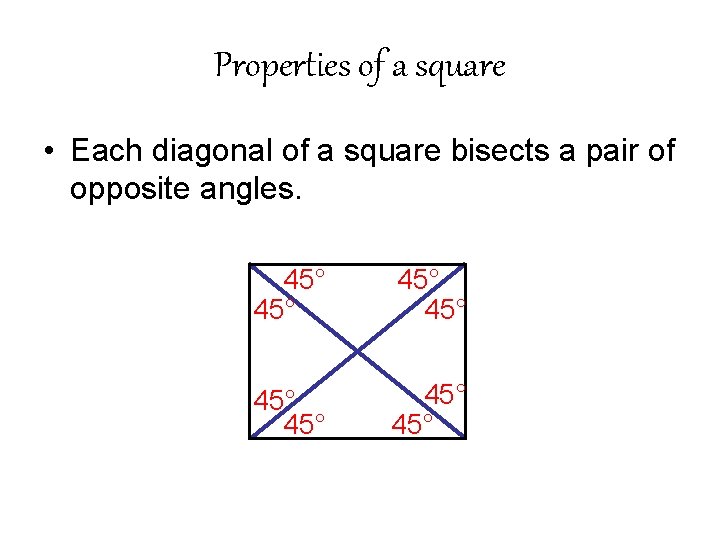
Properties of a square • Each diagonal of a square bisects a pair of opposite angles. 45° 45°

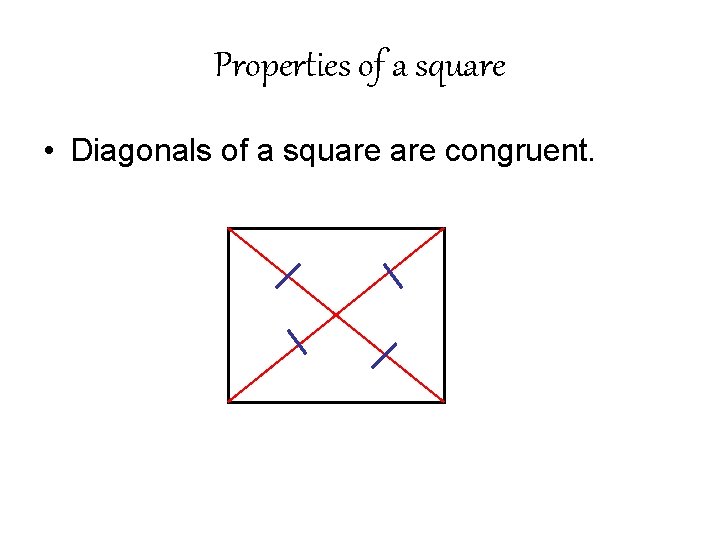
Properties of a square • Diagonals of a square congruent.

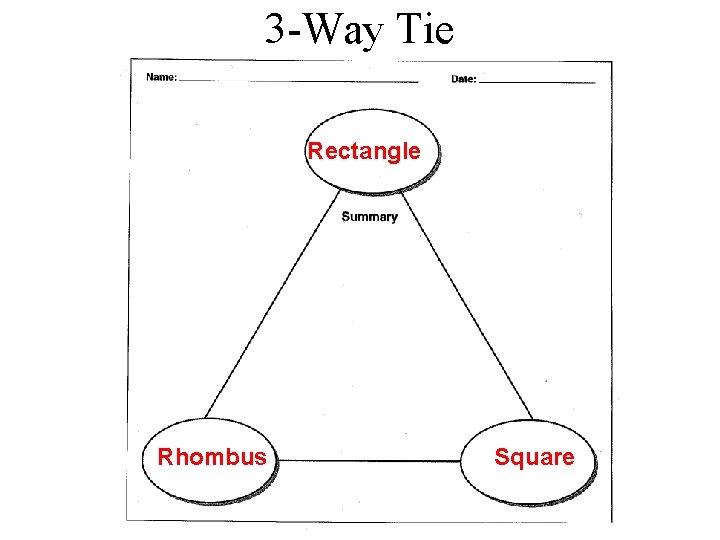
3 -Way Tie Rectangle Rhombus Square

Section 6. 5 Trapezoids and Kites

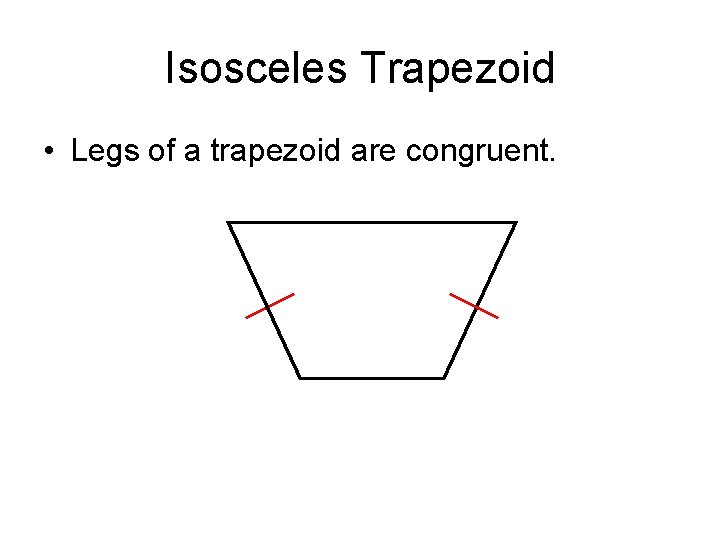
Trapezoid • Quadrilateral with exactly one pair of parallel sides. • Parallel sides are the bases. • Two pairs of base angles. • Nonparallel sides are the legs. Base > Leg > Base

Isosceles Trapezoid • Legs of a trapezoid are congruent.

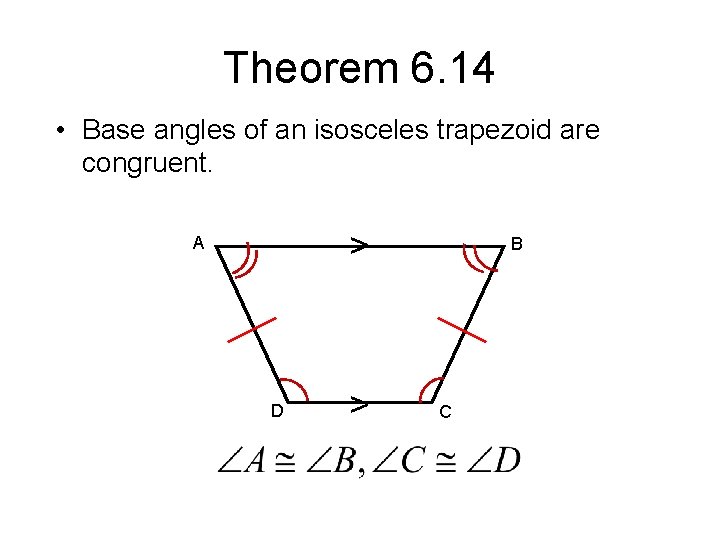
Theorem 6. 14 • Base angles of an isosceles trapezoid are congruent. > A D > B C

Theorem 6. 15 • If a trapezoid has one pair of congruent base angles, then it is an isosceles trapezoid. > A D > B C ABCD is an isosceles trapezoid

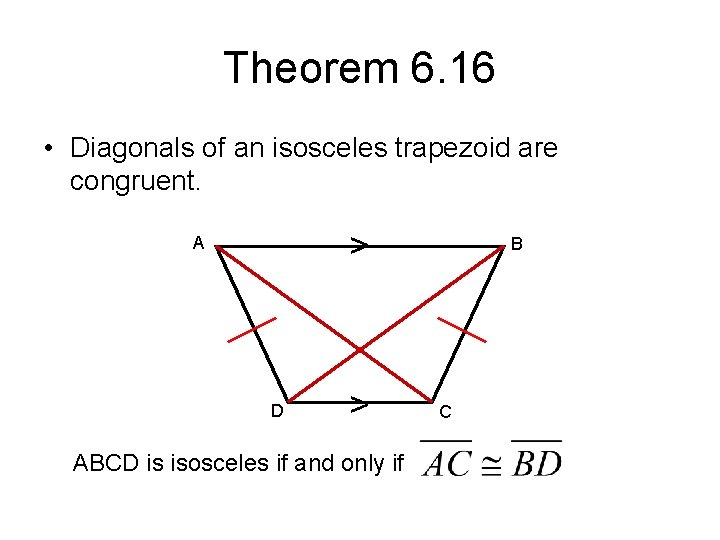
Theorem 6. 16 • Diagonals of an isosceles trapezoid are congruent. > A D > ABCD is isosceles if and only if B C

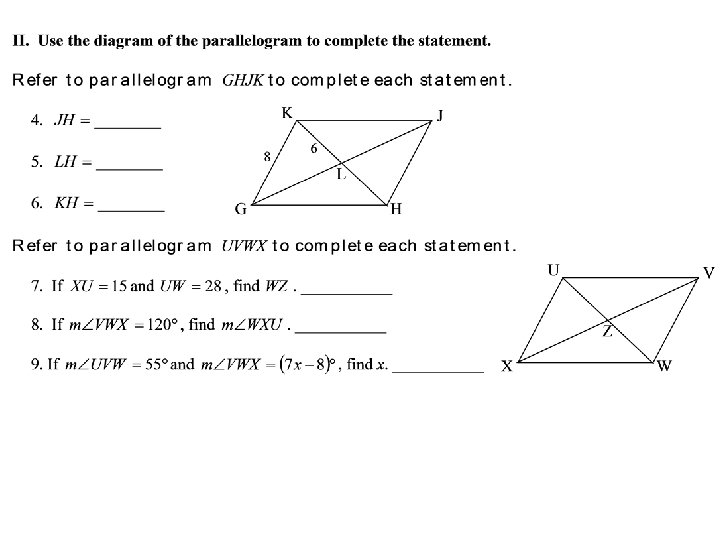
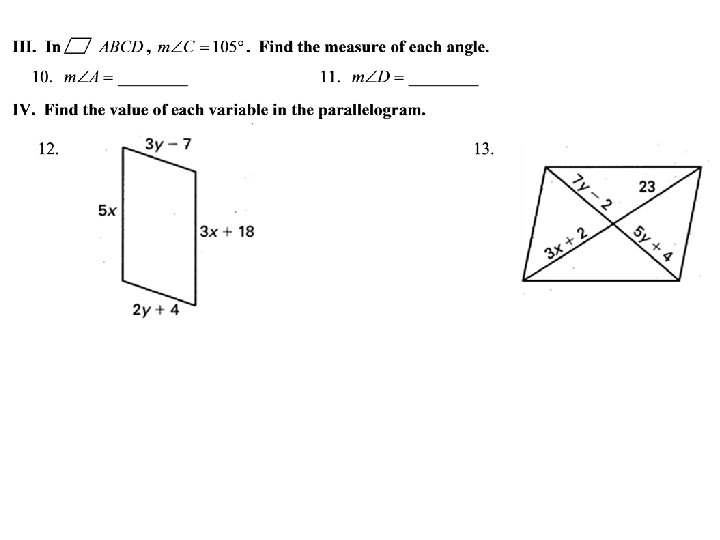
Examples on Board

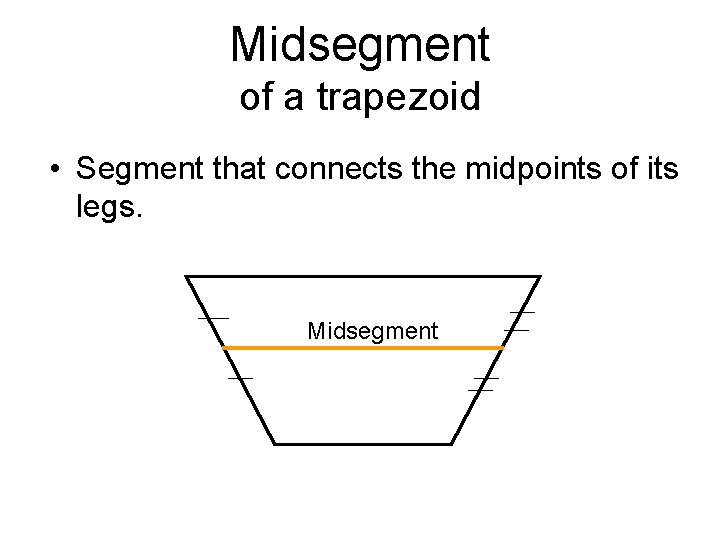
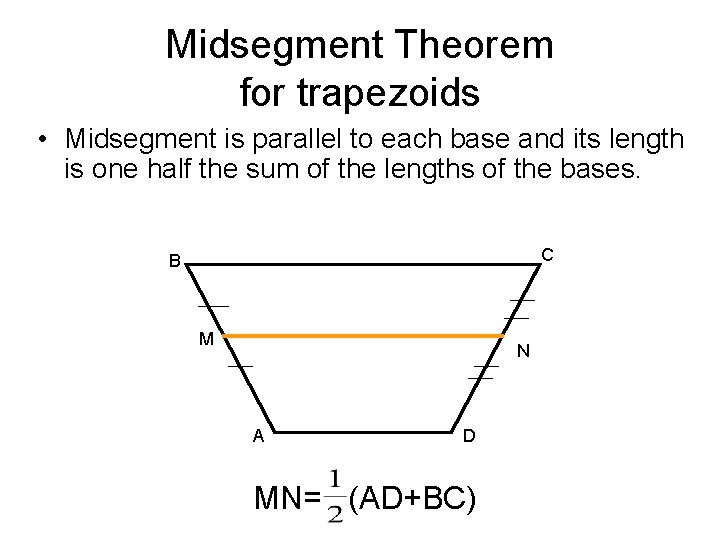
Midsegment of a trapezoid • Segment that connects the midpoints of its legs. Midsegment

Midsegment Theorem for trapezoids • Midsegment is parallel to each base and its length is one half the sum of the lengths of the bases. C B M N A D MN= (AD+BC)

Examples on Board

Kite • Quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.

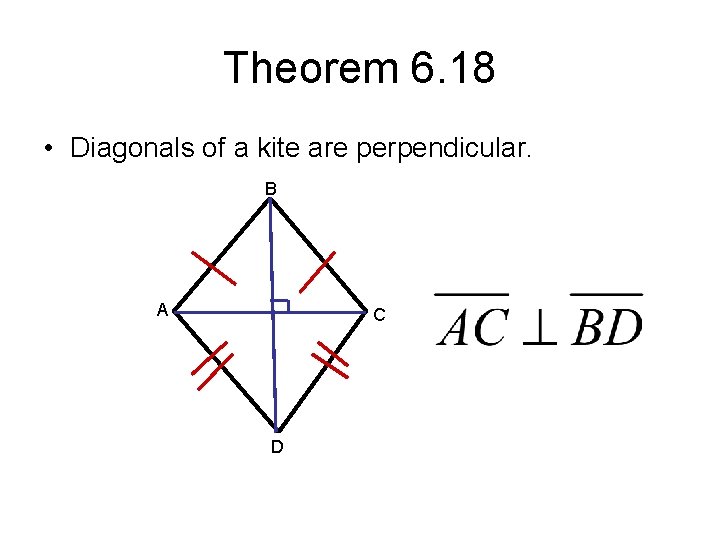
Theorem 6. 18 • Diagonals of a kite are perpendicular. B A C D

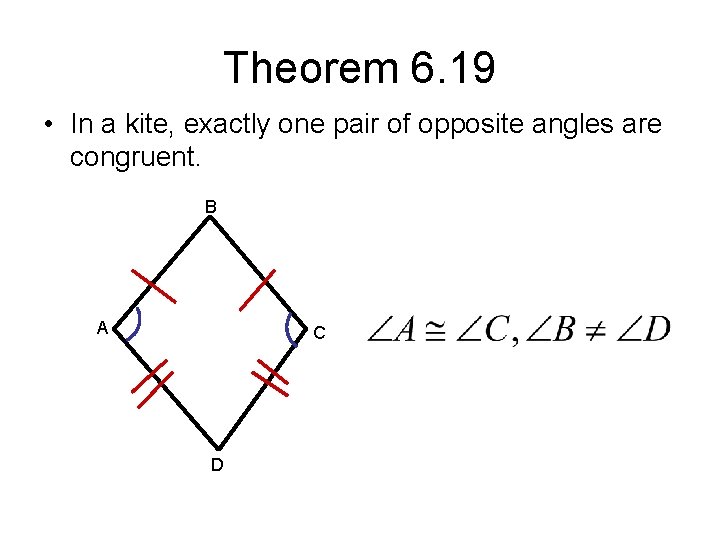
Theorem 6. 19 • In a kite, exactly one pair of opposite angles are congruent. B A C D

Examples on Board

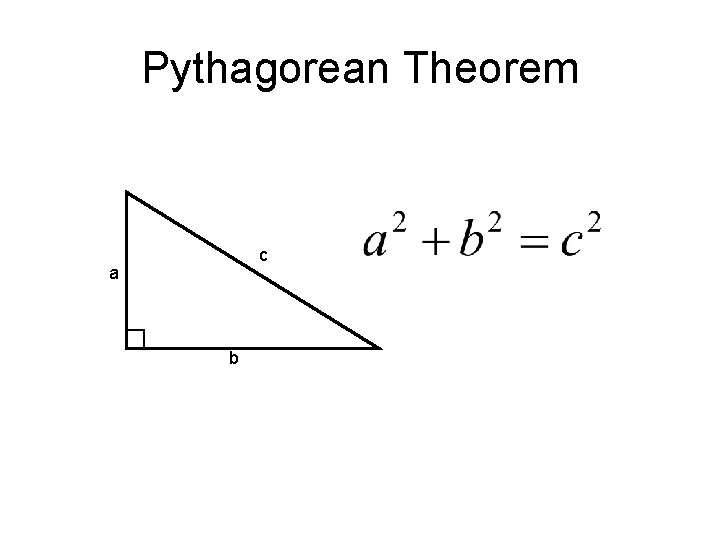
Pythagorean Theorem c a b

Section 6. 6 Special Quadrilaterals

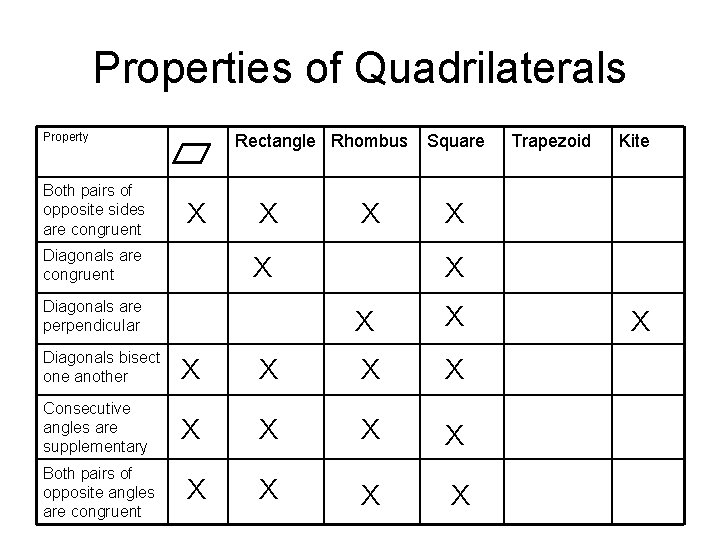
Properties of Quadrilaterals Property Both pairs of opposite sides are congruent Rectangle Rhombus X Diagonals are congruent X X X Diagonals are perpendicular Square Kite X X Diagonals bisect one another X X Consecutive angles are supplementary X X X X Both pairs of opposite angles are congruent Trapezoid X

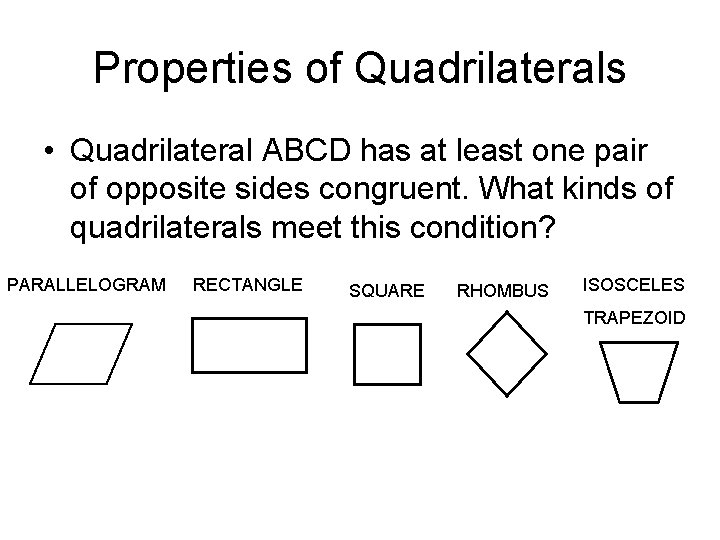
Properties of Quadrilaterals • Quadrilateral ABCD has at least one pair of opposite sides congruent. What kinds of quadrilaterals meet this condition? PARALLELOGRAM RECTANGLE SQUARE RHOMBUS ISOSCELES TRAPEZOID

Section 6. 7 Areas of Triangles and Quadrilaterals

Area Congruence Postulate • If two polygons are congruent, then they have the same area.

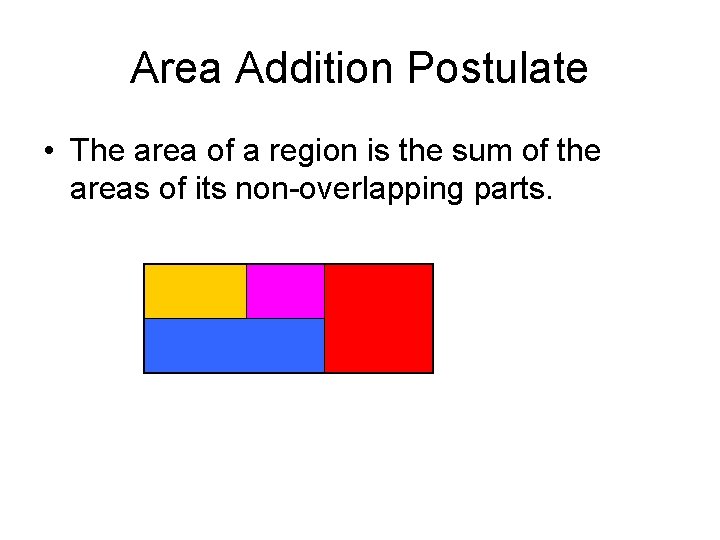
Area Addition Postulate • The area of a region is the sum of the areas of its non-overlapping parts.

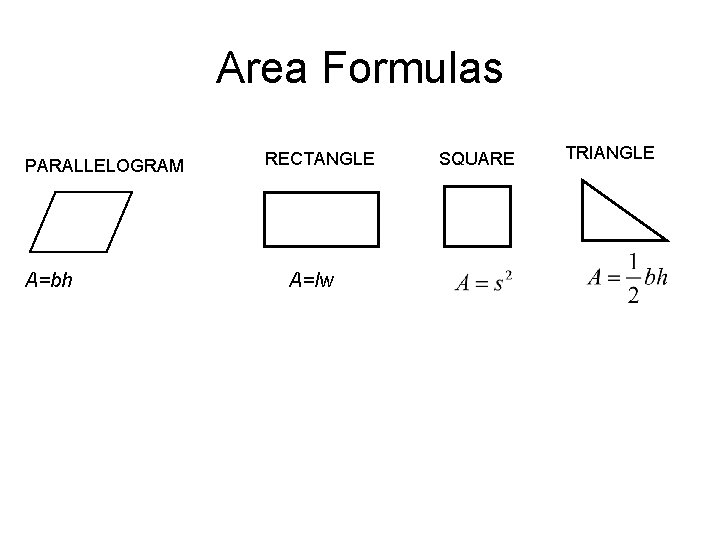
Area Formulas PARALLELOGRAM A=bh RECTANGLE A=lw SQUARE TRIANGLE

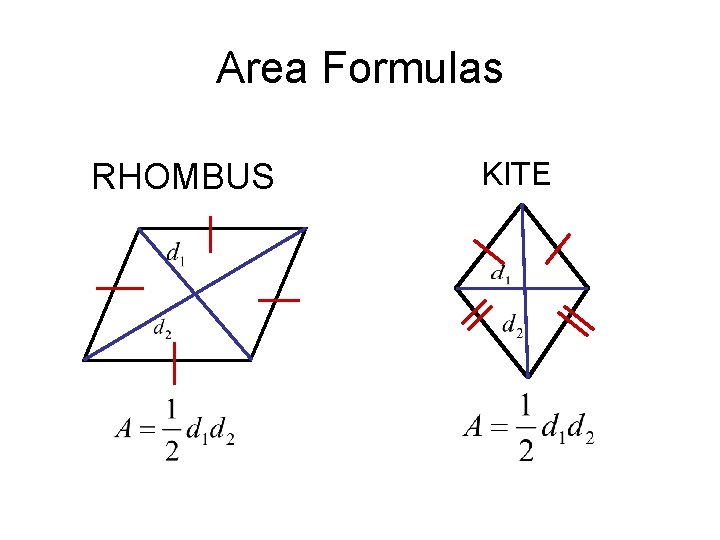
Area Formulas RHOMBUS KITE

Area Formulas TRAPEZOID h