Lesson 4 4 4 5 Proving s Congruent

Lesson 4 -4 & 4. 5: Proving Δs Congruent TARGETS • Use the SSS, SAS, ASA, AAS Postulates to test for triangle congruence.

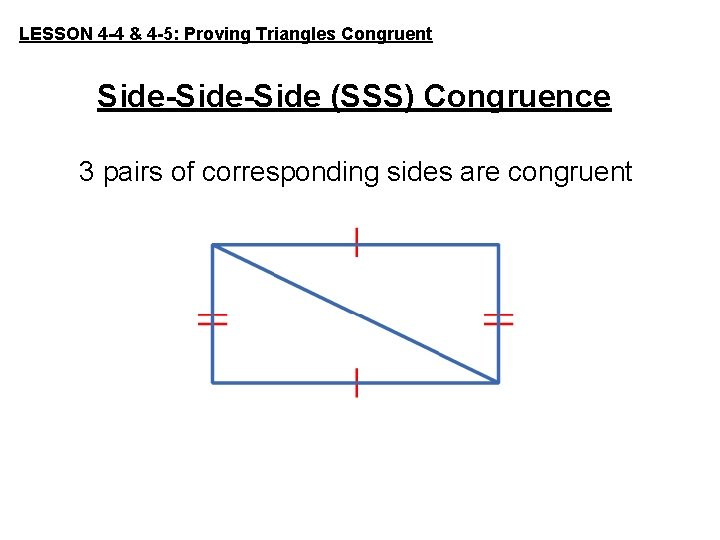
LESSON 4 -4 & 4 -5: Proving Triangles Congruent Side-Side (SSS) Congruence 3 pairs of corresponding sides are congruent

LESSON 4 -4 & 4 -5: Proving Triangles Congruent Side-Angle-Side (SAS) Congruence 2 pairs of corresponding sides and their included angles are congruent

LESSON 4 -4 & 4 -5: Proving Triangles Congruent Angle-Side-Angle (ASA) Congruence 2 pairs of corresponding angles and their included sides are congruent

LESSON 4 -4 & 4 -5: Proving Triangles Congruent Angle-Side (AAS) Congruence 2 pairs of corresponding angles and their non-included sides are congruent

LESSON 4 -4 & 4 -5: Proving Triangles Congruent Which Method? AAS SSS ASA

LESSON 4 -4: SSS, SAS Congruence EXAMPLE 2 EXTENDED RESPONSE Triangle DVW has vertices D(– 5, – 1), V(– 1, – 2), and W(– 7, – 4). Triangle LPM has vertices L(1, – 5), P(2, – 1), and M(4, – 7). a. Graph both triangles on the same coordinate plane. b. Use your graph to make a conjecture as to whether the triangles are congruent. Explain your reasoning. c. Write a logical argument that uses coordinate geometry to support the conjecture you made in part b.

Read the Test Item You are asked to do three things in this problem. In part a, you are to graph ΔDVW and ΔLPM on the same coordinate plane. In part b, you should make a conjecture that ΔDVW ΔLPM or ΔDVW / ΔLPM based on your graph. Finally, in part c, you are asked to prove your conjecture. Solve the Test Item a.

b. From the graph, it appears that the triangles have the same shapes, so we conjecture that they are congruent. c. Use the Distance Formula to show all corresponding sides have the same measure.

Answer: WD = ML, DV = LP, and VW = PM. By definition of congruent segments, all corresponding segments are congruent. Therefore, ΔWDV ΔMLP by SSS.

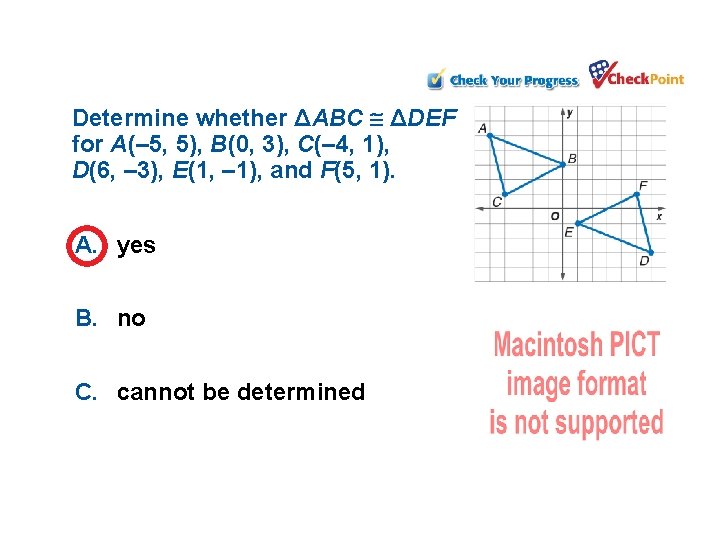
Determine whether ΔABC ΔDEF for A(– 5, 5), B(0, 3), C(– 4, 1), D(6, – 3), E(1, – 1), and F(5, 1). A. yes B. no C. cannot be determined 1. 2. 3. A B C