Unit 4 Lesson 4 Prove Triangles Congruent by

Unit 4 Lesson 4 Prove Triangles Congruent by ASA and AAS

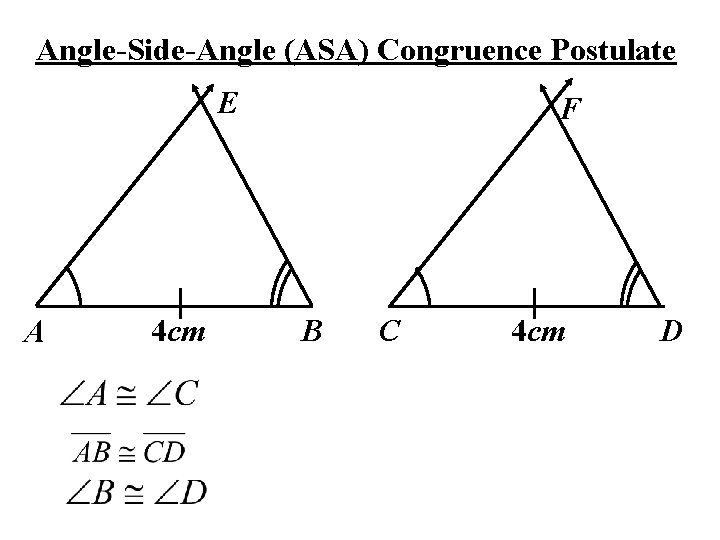
Angle-Side-Angle (ASA) Congruence Postulate E A 4 cm F B C 4 cm D

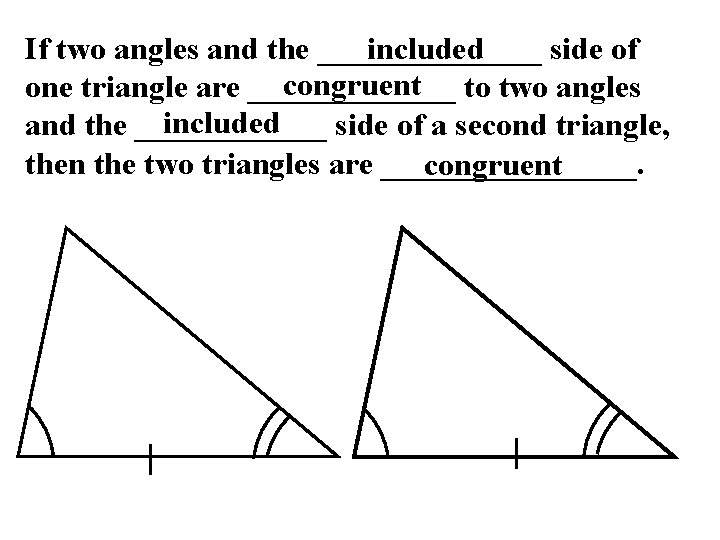
If two angles and the _______ side of included congruent to two angles one triangle are _______ included and the ______ side of a second triangle, then the two triangles are ________. congruent

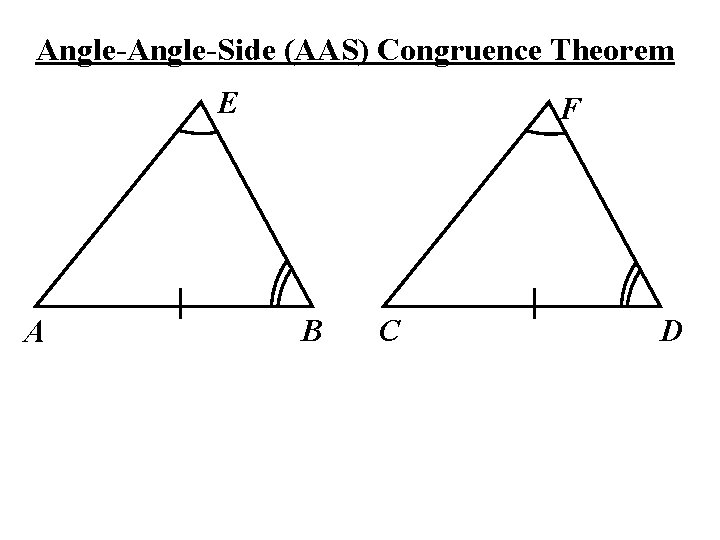
Angle-Side (AAS) Congruence Theorem E A F B C D

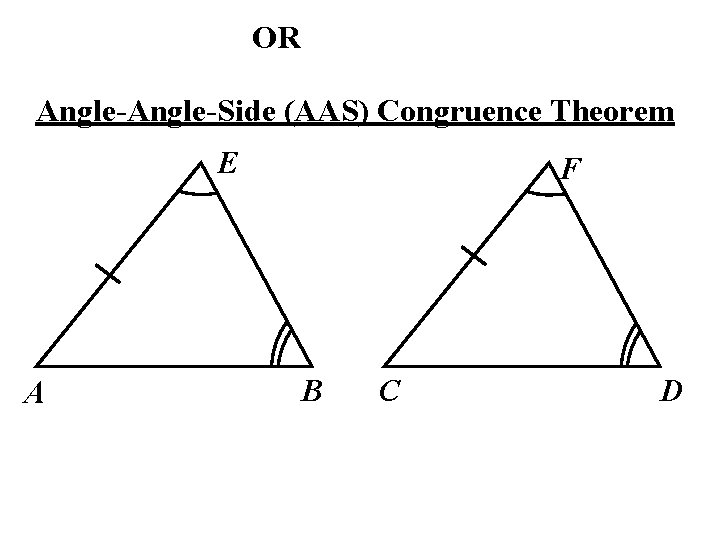
OR Angle-Side (AAS) Congruence Theorem E A F B C D

nonincluded If two angles and a ___________ congruent side of one triangle are ________ to two angles and the corresponding nonincluded __________ side of a second triangle, then the two triangles are congruent ________.

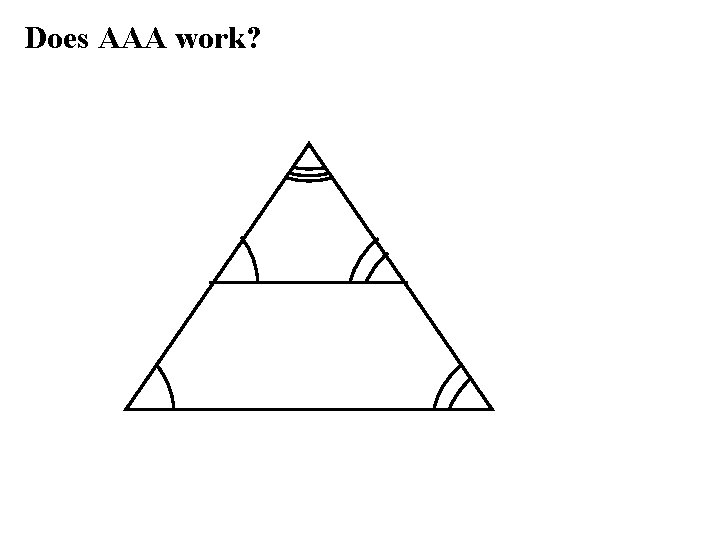
Does AAA work?

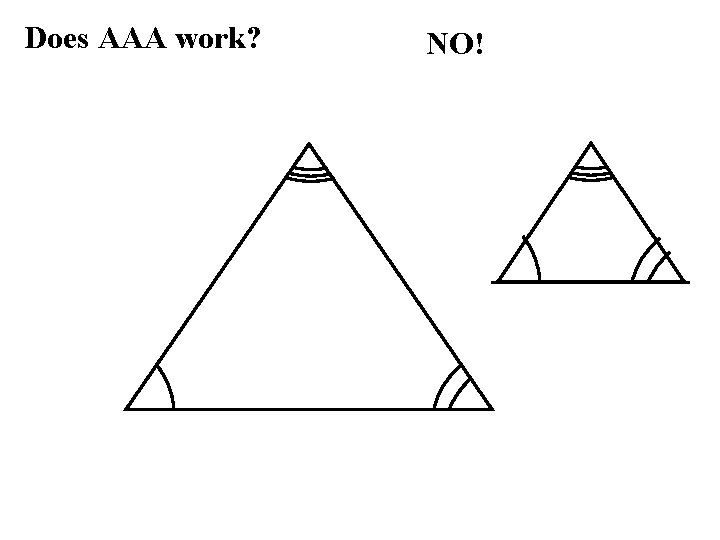
Does AAA work? NO!

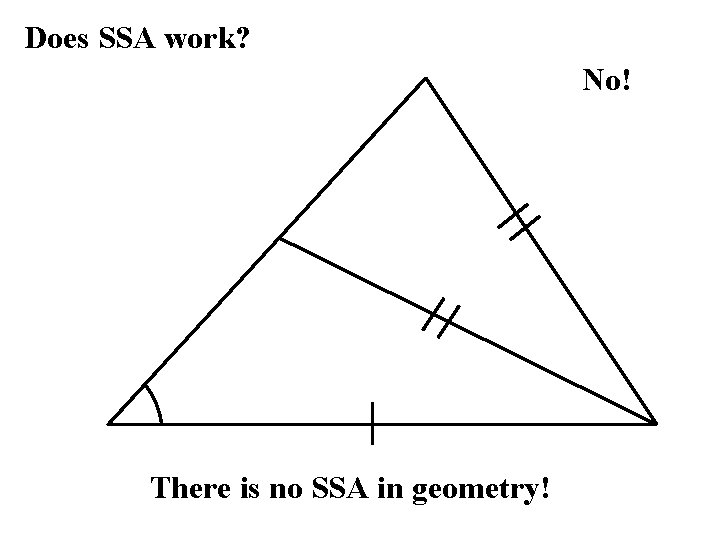
Does SSA work? No! There is no SSA in geometry!

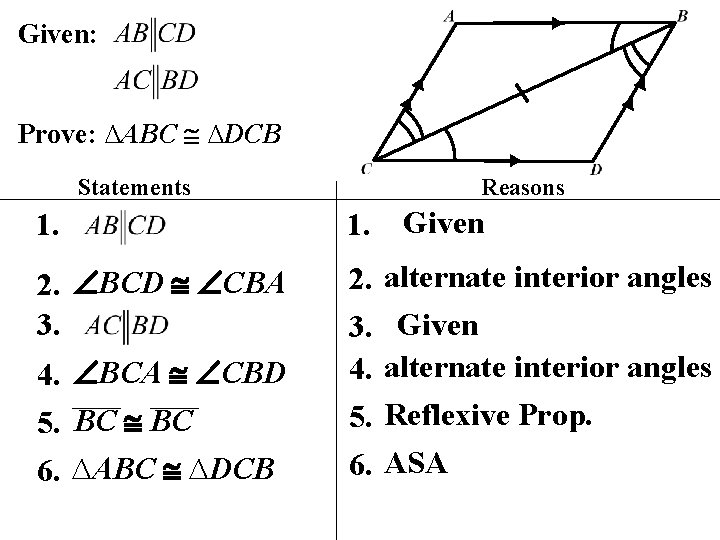
Given: Prove: ∆ABC ∆DCB Statements Reasons 1. 2. BCD CBA 3. 2. 3. 4. 5. 6. 4. BCA CBD 5. BC 6. ∆ABC ∆DCB Given alternate interior angles Reflexive Prop. ASA

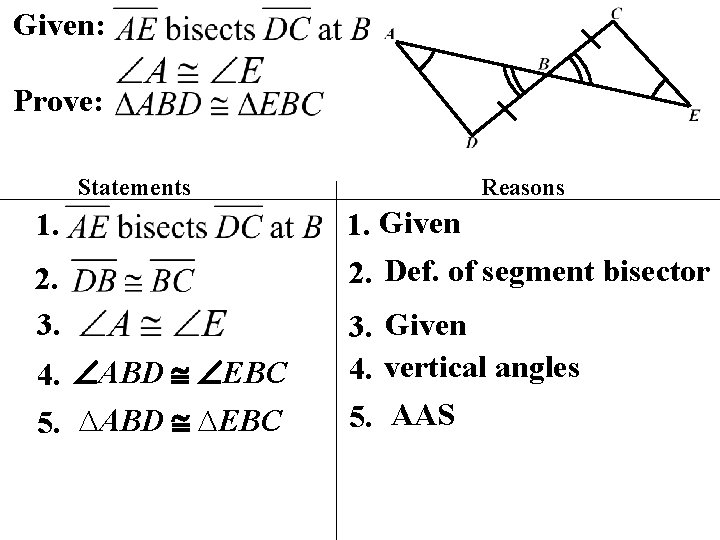
Given: Prove: Statements 1. 2. 3. 4. ABD EBC 5. ∆ABD ∆EBC Reasons 1. Given 2. Def. of segment bisector 3. Given 4. vertical angles 5. AAS

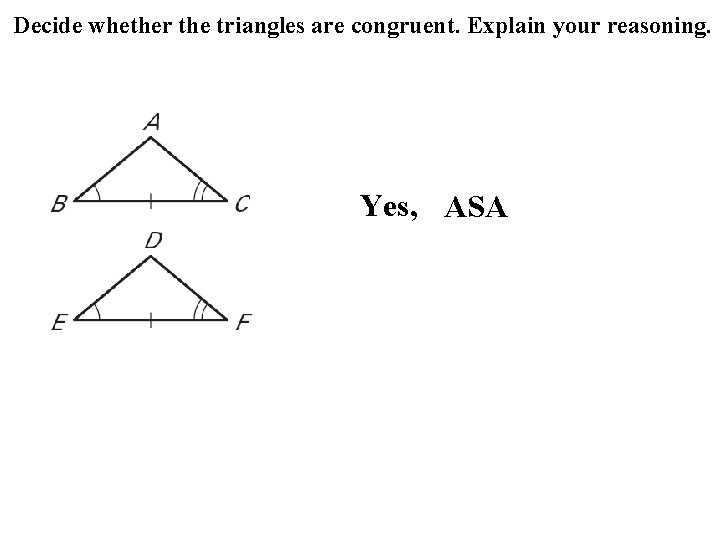
Decide whether the triangles are congruent. Explain your reasoning. Yes, ASA

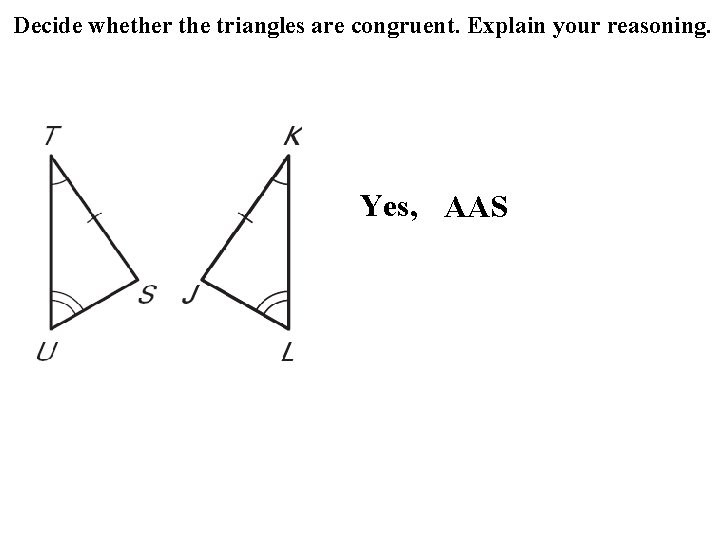
Decide whether the triangles are congruent. Explain your reasoning. Yes, AAS

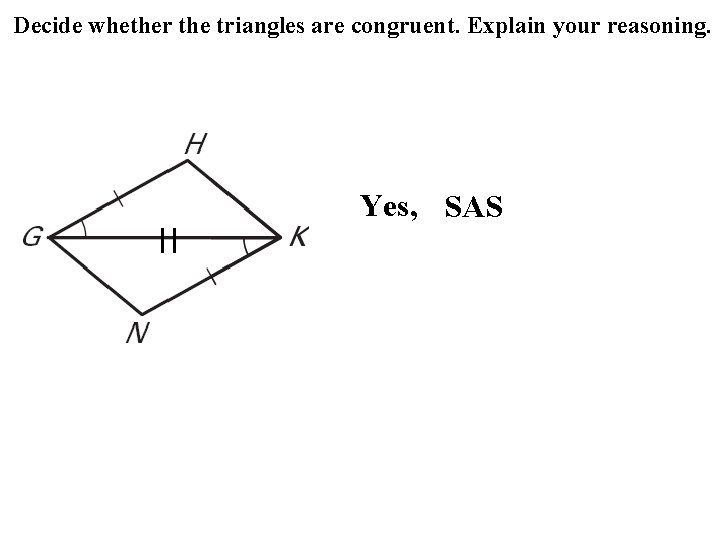
Decide whether the triangles are congruent. Explain your reasoning. Yes, SAS

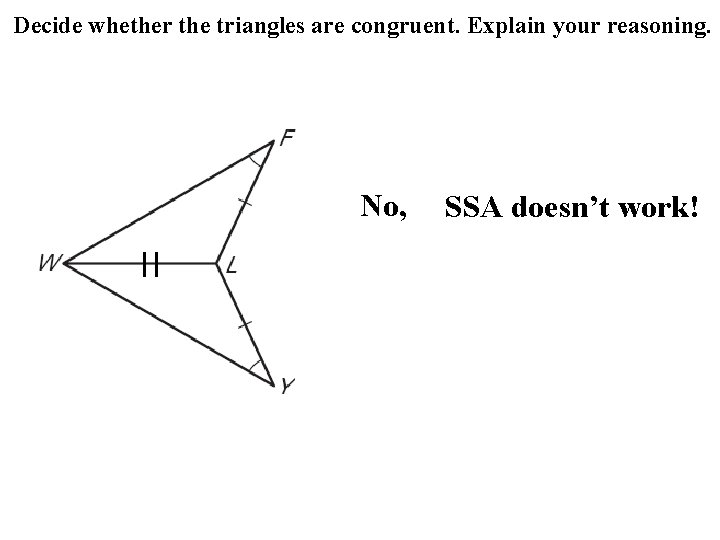
Decide whether the triangles are congruent. Explain your reasoning. No, SSA doesn’t work!

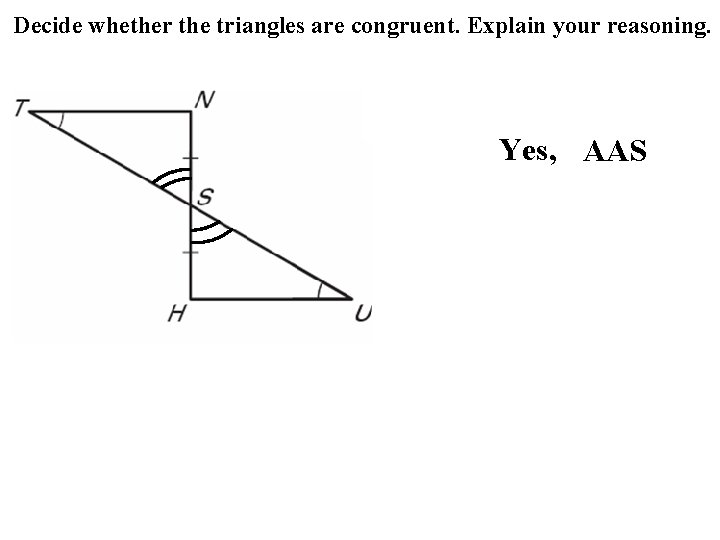
Decide whether the triangles are congruent. Explain your reasoning. Yes, AAS

HW Problem LT 4. 2 Assignment 4. 5 Worksheet Due