Congruent triangles Warm Up Lesson Presentation Lesson Quiz





















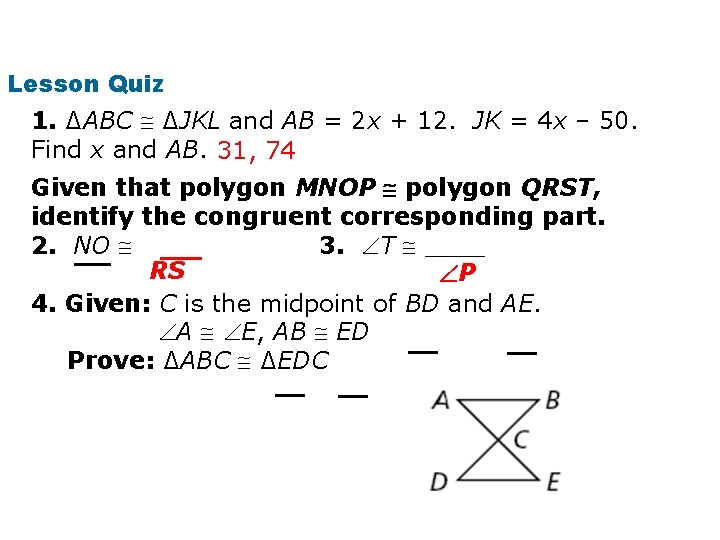
- Slides: 25

Congruent triangles Warm Up Lesson Presentation Lesson Quiz

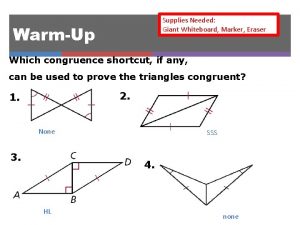
Warm Up 1. Name all sides and angles of ∆FGH. FG, GH, FH, F, G, H 2. What is true about K and L? Why? ; Third s Thm. 3. What does it mean for two segments to be congruent? They have the same length.

Objectives Use properties of congruent triangles. Prove triangles congruent by using the definition of congruence.

Vocabulary corresponding angles corresponding sides congruent polygons

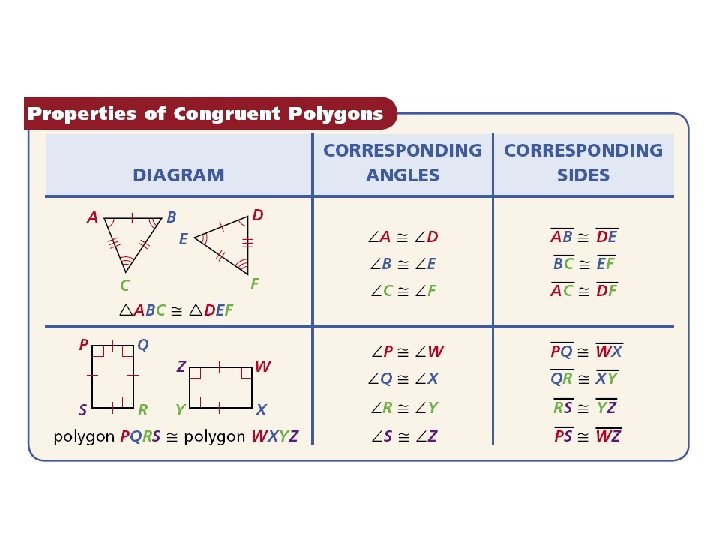
Geometric figures are congruent if they are the same size and shape. Corresponding angles and corresponding sides are in the same position in polygons with an equal number of sides. Two polygons are congruent polygons if and only if their corresponding sides are congruent. Thus triangles that are the same size and shape are congruent.


Helpful Hint Two vertices that are the endpoints of a side are called consecutive vertices. For example, P and Q are consecutive vertices.

To name a polygon, write the vertices in consecutive order. For example, you can name polygon PQRS as QRSP or SRQP, but not as PRQS. In a congruence statement, the order of the vertices indicates the corresponding parts.

Helpful Hint When you write a statement such as ABC DEF, you are also stating which parts are congruent.

Example 1: Naming Congruent Corresponding Parts Given: ∆PQR ∆STW Identify all pairs of corresponding congruent parts. Angles: P S, Q T, R W Sides: PQ ST, QR TW, PR SW

Check It Out! Example 1 If polygon LMNP polygon EFGH, identify all pairs of corresponding congruent parts. Angles: L E, M F, N G, P H Sides: LM EF, MN FG, NP GH, LP EH

Example 2 A: Using Corresponding Parts of Congruent Triangles Given: ∆ABC ∆DBC. Find the value of x. BCA and BCD are rt. s. Def. of lines. BCA BCD Rt. Thm. m BCA = m BCD Def. of s (2 x – 16)° = 90° 2 x = 106 x = 53 Substitute values for m BCA and m BCD. Add 16 to both sides. Divide both sides by 2.

Example 2 B: Using Corresponding Parts of Congruent Triangles Given: ∆ABC ∆DBC. Find m DBC. m ABC + m BCA + m A = 180° ∆ Sum Thm. Substitute values for m BCA and m ABC + 139. 3 = 180 Simplify. m ABC + 90 + 49. 3 = 180 m ABC = 40. 7 DBC ABC Subtract 139. 3 from both sides. Corr. s of ∆s are . m DBC = m ABC Def. of s. m DBC 40. 7° Trans. Prop. of =

Check It Out! Example 2 a Given: ∆ABC ∆DEF Find the value of x. AB DE Corr. sides of ∆s are . AB = DE Def. of parts. 2 x – 2 = 6 2 x = 8 x=4 Substitute values for AB and DE. Add 2 to both sides. Divide both sides by 2.

Check It Out! Example 2 b Given: ∆ABC ∆DEF Find m F. m EFD + m DEF + m FDE = 180° ABC DEF ∆ Sum Thm. Corr. s of ∆ are . m ABC = m DEF Def. of s. m DEF = 53° Transitive Prop. of =. m EFD + 53 + 90 = 180 m F + 143 = 180 m F = 37° Substitute values for m DEF and m FDE. Simplify. Subtract 143 from both sides.

Example 3: Proving Triangles Congruent Given: YWX and YWZ are right angles. YW bisects XYZ. W is the midpoint of XZ. XY YZ. Prove: ∆XYW ∆ZYW

Statements Reasons 1. YWX and YWZ are rt. s. 1. Given 2. YWX YWZ 2. Rt. Thm. 3. YW bisects XYZ 3. Given 4. XYW ZYW 4. Def. of bisector 5. W is mdpt. of XZ 5. Given 6. XW ZW 6. Def. of mdpt. 7. YW 7. Reflex. Prop. of 8. X Z 8. Third s Thm. 9. XY YZ 9. Given 10. ∆XYW ∆ZYW 10. Def. of ∆

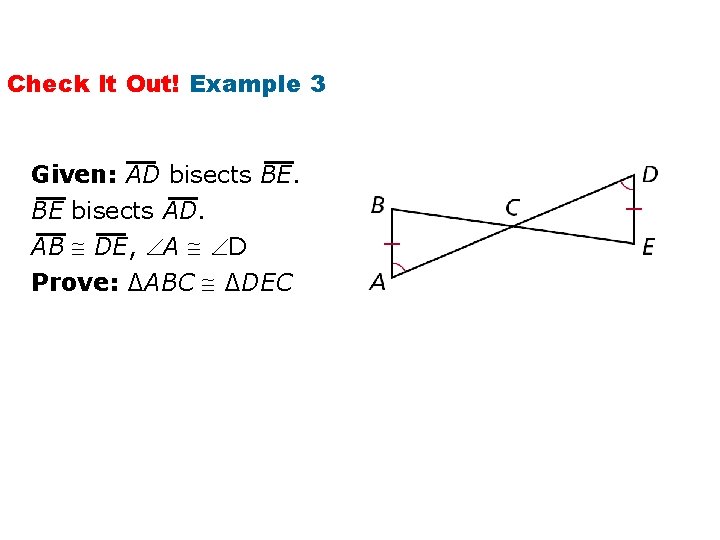
Check It Out! Example 3 Given: AD bisects BE. BE bisects AD. AB DE, A D Prove: ∆ABC ∆DEC

Statements Reasons 1. A D 1. Given 2. BCA DCE 2. Vertical s are . 3. ABC DEC 3. Third s Thm. 4. AB DE 4. Given 5. AD bisects BE, 5. Given BE bisects AD 6. BC EC, 7. ∆ABC ∆DEC AC DC 6. Def. of bisector 7. Def. of ∆s

Example 4: Engineering Application The diagonal bars across a gate give it support. Since the angle measures and the lengths of the corresponding sides are the same, the triangles are congruent. Given: PR and QT bisect each other. PQS RTS, QP RT Prove: ∆QPS ∆TRS

Example 4 Continued Statements Reasons 1. QP RT 1. Given 2. PQS RTS 2. Given 3. PR and QT bisect each other. 3. Given 4. QS TS, PS RS 4. Def. of bisector 5. QSP TSR 5. Vert. s Thm. 6. QSP TRS 6. Third s Thm. 7. ∆QPS ∆TRS 7. Def. of ∆s

Check It Out! Example 4 Use the diagram to prove the following. Given: MK bisects JL. JL bisects MK. JK ML. JK || ML. Prove: ∆JKN ∆LMN

Check It Out! Example 4 Continued Statements Reasons 1. JK ML 1. Given 2. JK || ML 2. Given 3. JKN NML 3. Alt int. s are . 4. JL and MK bisect each other. 4. Given 5. JN LN, MN KN 5. Def. of bisector 6. KNJ MNL 6. Vert. s Thm. 7. KJN MLN 7. Third s Thm. 8. ∆JKN ∆LMN 8. Def. of ∆s
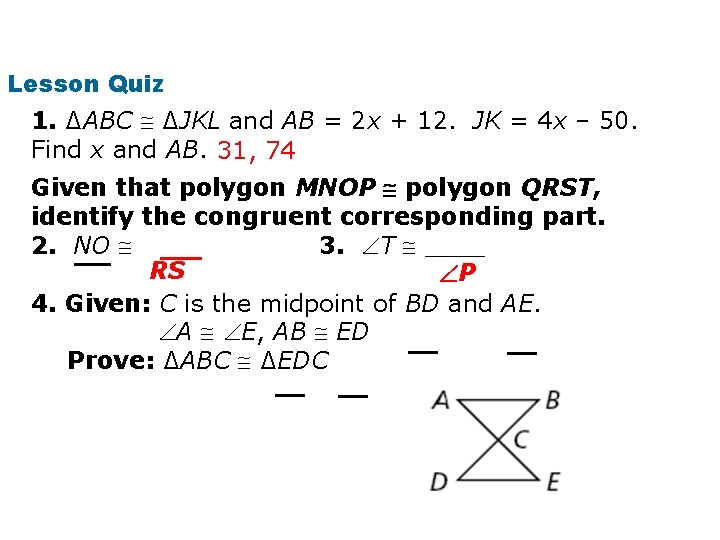
Lesson Quiz 1. ∆ABC ∆JKL and AB = 2 x + 12. JK = 4 x – 50. Find x and AB. 31, 74 Given that polygon MNOP polygon QRST, identify the congruent corresponding part. 2. NO ____ 3. T ____ RS P 4. Given: C is the midpoint of BD and AE. A E, AB ED Prove: ∆ABC ∆EDC

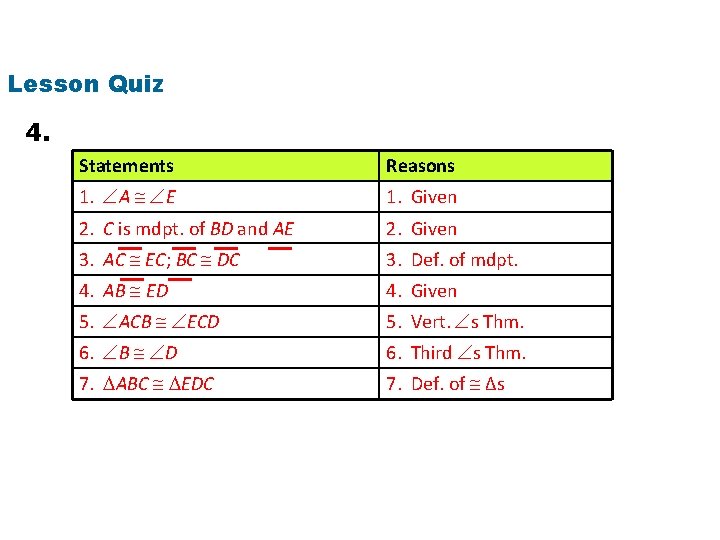
Lesson Quiz 4. Statements Reasons 1. A E 1. Given 2. C is mdpt. of BD and AE 2. Given 3. AC EC; BC DC 3. Def. of mdpt. 4. AB ED 4. Given 5. ACB ECD 5. Vert. s Thm. 6. B D 6. Third s Thm. 7. ABC EDC 7. Def. of ∆s
 If pqr tsr what are the congruent corresponding parts
If pqr tsr what are the congruent corresponding parts Congruent triangles isosceles and equilateral triangles
Congruent triangles isosceles and equilateral triangles 4-3 proving triangles congruent sss sas
4-3 proving triangles congruent sss sas Unit 4 congruent triangles homework 3
Unit 4 congruent triangles homework 3 4-4 lesson quiz geometry
4-4 lesson quiz geometry Quiz 4-1 congruent triangles
Quiz 4-1 congruent triangles Quiz 4-2 congruent triangles sss and sas
Quiz 4-2 congruent triangles sss and sas 4-4 triangle congruence sss and sas
4-4 triangle congruence sss and sas Included angle
Included angle Lesson 4-5 proving triangles congruent
Lesson 4-5 proving triangles congruent Asa geometry example
Asa geometry example 4-4 proving triangles congruent
4-4 proving triangles congruent Classify each polygon
Classify each polygon Vertical angles are congruent
Vertical angles are congruent 7-4 lesson quiz similarity in right triangles
7-4 lesson quiz similarity in right triangles 8-1 similarity in right triangles answer key
8-1 similarity in right triangles answer key Write the specified type of proof
Write the specified type of proof 4-4 congruent triangles
4-4 congruent triangles Similar and congruent triangles
Similar and congruent triangles Giant white board
Giant white board How to determine triangle congruence
How to determine triangle congruence Dr frost proof
Dr frost proof Congruent triangles worksheet
Congruent triangles worksheet Rhs congruence rule
Rhs congruence rule 4-1 congruent figures
4-1 congruent figures Triangle congruence matching activity
Triangle congruence matching activity