4 4 Proving Congruence SSS and SAS What

4. 4 Proving Congruence – SSS and SAS What you’ll learn: 1. To use SSS Postulate to test for triangle congruence. 2. To use the SAS Postulate to test for triangle congruence.

More ways to prove 2 triangles are : Postulate 4. 1 SSS Congruence If the sides of one triangle are congruent to the sides of a second triangle, then the triangles are congruent. Postulate 4. 2 SAS Congruence If 2 sides and the included angle of one triangle are congruent to 2 sides and the included angle of another triangle, then the triangles are congruent.

Determine whether ABC DEF. Explain. A(-6, 1), B(1, 2), C(-1, -4), D(0, 5), E(7, 6), F(5, 0)

Assumables The following can be assumed from the given picture: 1. Vertical angles are congruent. (reason: vert. congruent) 2. A segment or angle shared by both triangles is congruent to itself. (reason: reflexive)

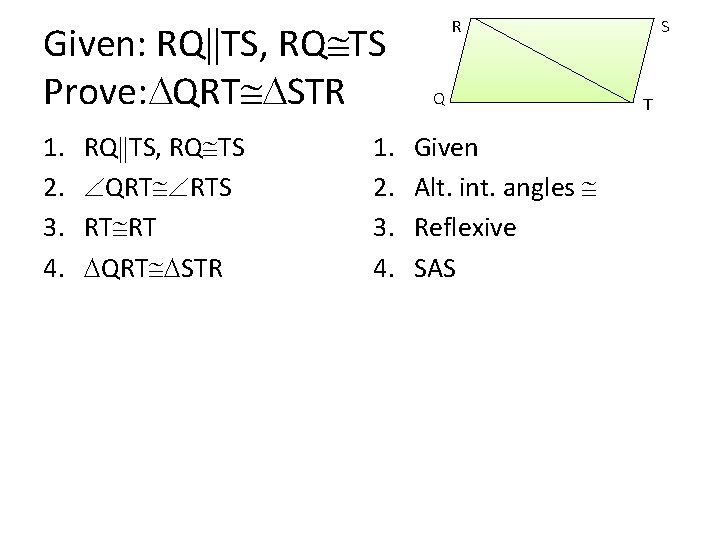
Given: RQ TS, RQ TS Prove: QRT STR 1. 2. 3. 4. RQ TS, RQ TS QRT RTS RT RT QRT STR 1. 2. 3. 4. R Q Given Alt. int. angles Reflexive SAS S T

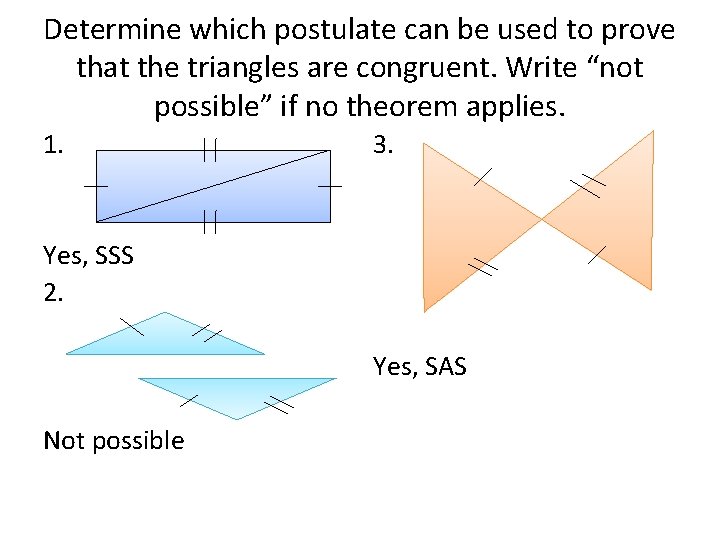
Determine which postulate can be used to prove that the triangles are congruent. Write “not possible” if no theorem applies. 1. 3. Yes, SSS 2. Yes, SAS Not possible

How to use CPCTC When you are asked to prove that corresponding parts (angles or sides) of 2 triangles are congruent, you may have to prove the 2 triangles are congruent first. Then by CPCTC, the corresponding parts are also congruent. A Ex: Given: B D, B D C AB AD, BC CD. Prove: BAC DAC Statements Reasons B D, AB AD, BC CD given CBA CDA SAS BAC DAC CPCTC

Homework p. 204 10 -22 even