Proving Triangles are Congruent SSS SAS ASA AAS













- Slides: 42

Proving Triangles are Congruent SSS, SAS; ASA; AAS CCSS: G. CO 7

Standards for Mathematical Practices • 1. Make sense of problems and persevere in solving them. • 2. Reason abstractly and quantitatively. • 3. Construct viable arguments and critique the reasoning of others. • 4. Model with mathematics. • 5. Use appropriate tools strategically. • 6. Attend to precision. • 7. Look for and make use of structure. • 8. Look for and express regularity in repeated reasoning.

CCSS: G. CO 7 • USE the definition of congruence in terms of rigid motions to SHOW that two triangles ARE congruent if and only if corresponding pairs of sides and corresponding pairs of angles ARE congruent.

ESSENTIAL QUESTION • How do we show that triangles are congruent? • How do we use triangle congruence to plane and write proves , and prove that constructions are valid?

Objectives: 1. Prove that triangles are congruent using the ASA Congruence Postulate and the AAS Congruence Theorem 2. Use congruence postulates and theorems in real-life problems.

Proving Triangles are Congruent: SSS and SAS

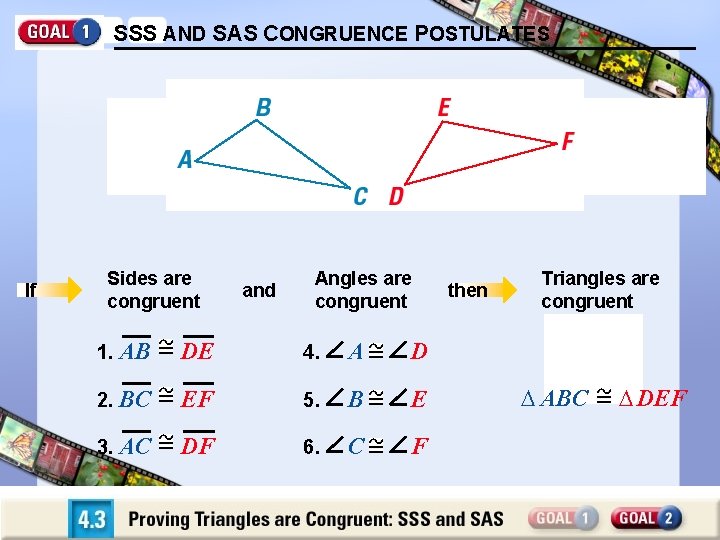
SSS AND SAS CONGRUENCE POSTULATES If all six pairs of corresponding parts (sides and angles) are congruent, then the triangles are congruent. If Sides are congruent and Angles are congruent 1. AB DE 4. A D 2. BC EF 5. B E 3. AC DF 6. C F then Triangles are congruent ABC DEF

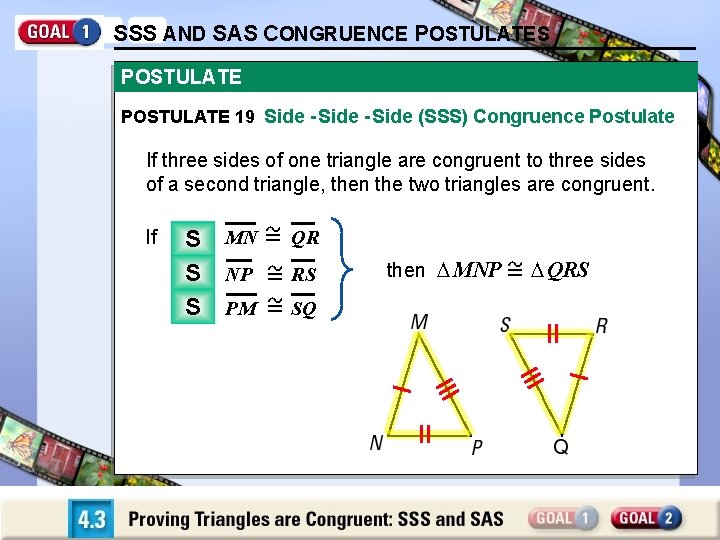
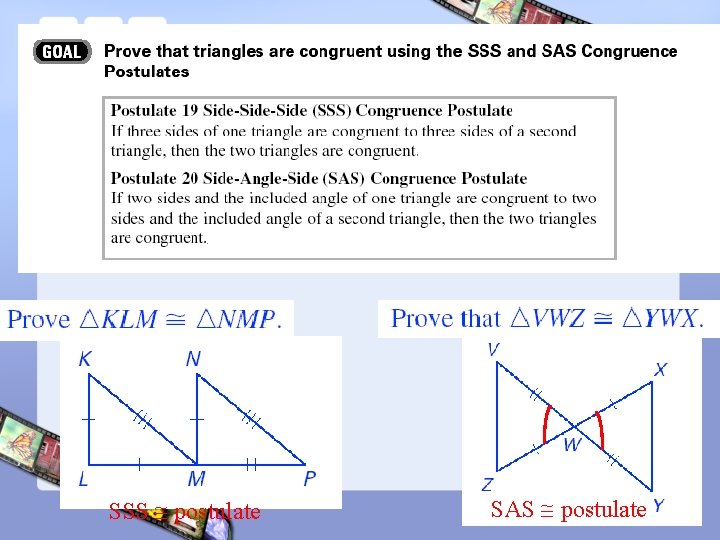
SSS AND SAS CONGRUENCE POSTULATES POSTULATE 19 Side - Side (SSS) Congruence Postulate If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent. If Side S MN QR Side S NP RS Side S PM SQ then MNP QRS

SSS AND SAS CONGRUENCE POSTULATES The SSS Congruence Postulate is a shortcut for proving two triangles are congruent without using all six pairs of corresponding parts.

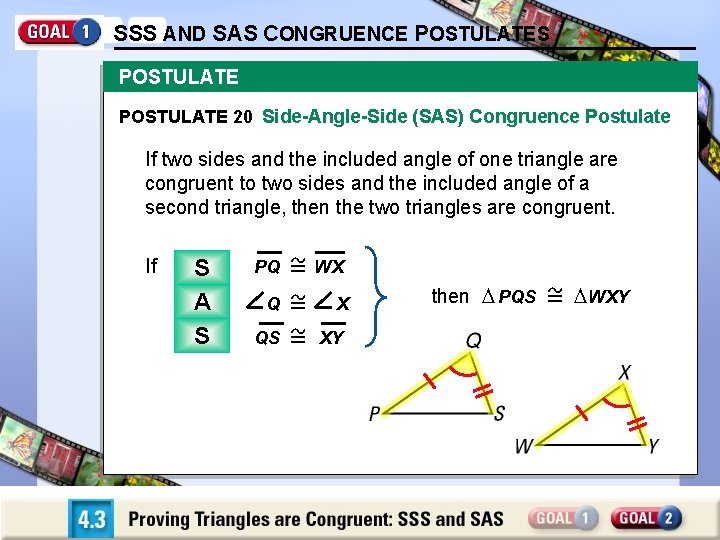
SSS AND SAS CONGRUENCE POSTULATES POSTULATE 20 Side-Angle-Side (SAS) Congruence Postulate If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent. If Side S Angle A Side S PQ WX Q X QS XY then PQS WXY

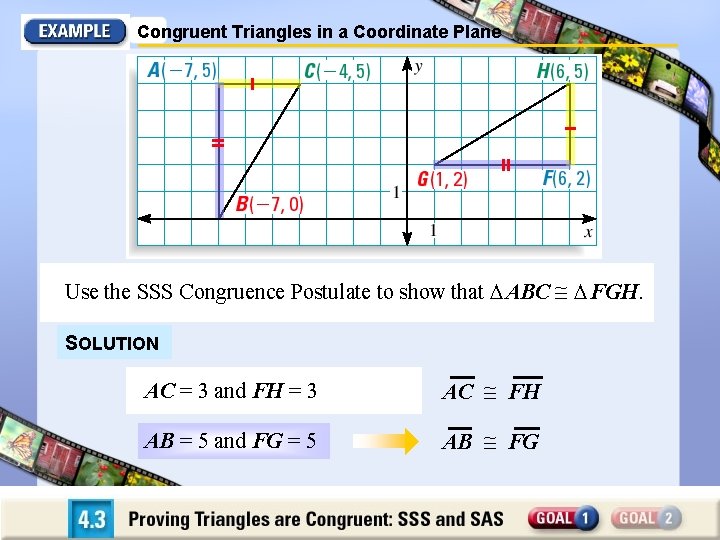
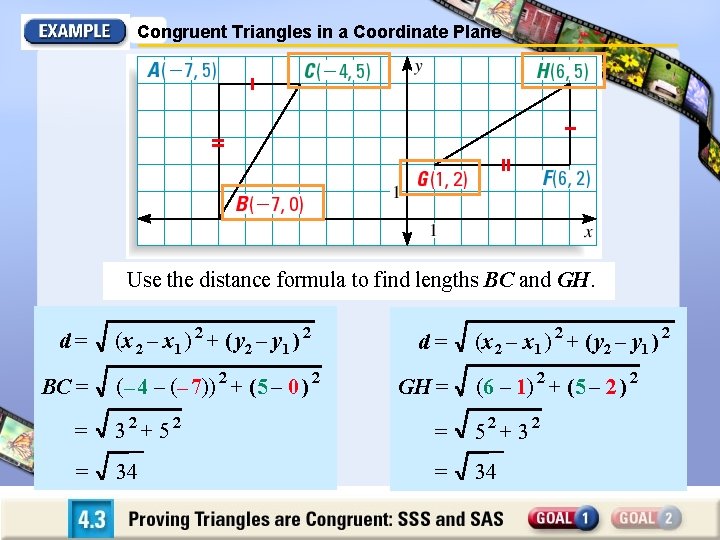
Congruent Triangles in a Coordinate Plane Use the SSS Congruence Postulate to show that ABC FGH. SOLUTION AC = 3 and FH = 3 AC FH AB = 5 and FG = 5 AB FG

Congruent Triangles in a Coordinate Plane Use the distance formula to find lengths BC and GH. d= BC = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (– 4 – (– 7)) 2 + (5 – 0 ) 2 d= GH = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (6 – 1) 2 + (5 – 2 ) 2 = 32 + 52 = 52 + 32 = 34

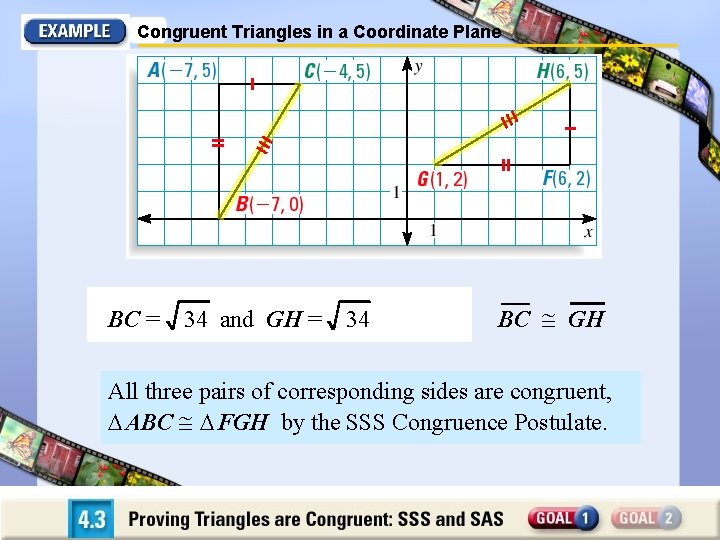
Congruent Triangles in a Coordinate Plane BC = 34 and GH = 34 BC GH All three pairs of corresponding sides are congruent, ABC FGH by the SSS Congruence Postulate.

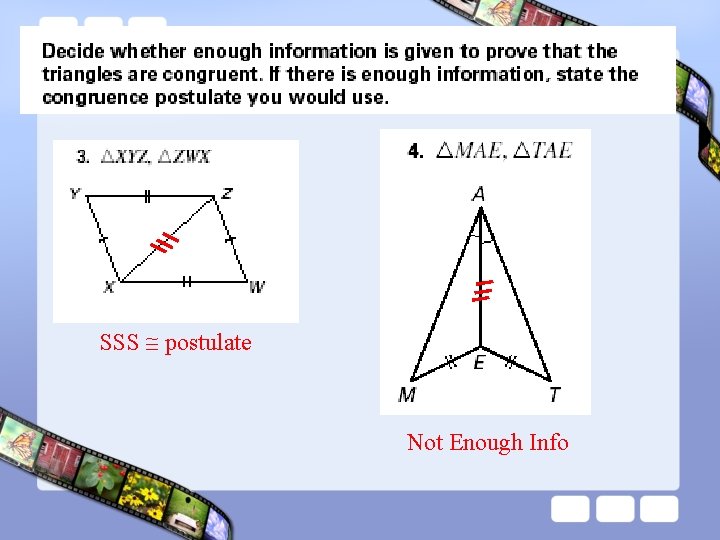
SSS postulate SAS postulate

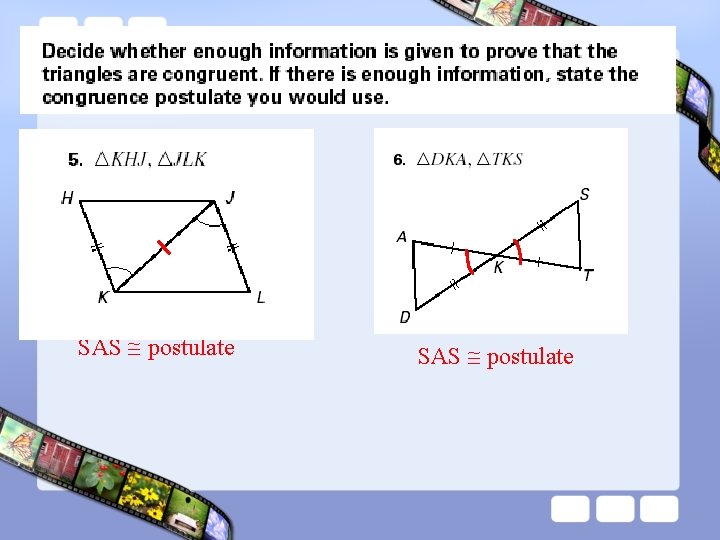
T S C G The vertex of the included angle is the point in common. SAS postulate SSS postulate

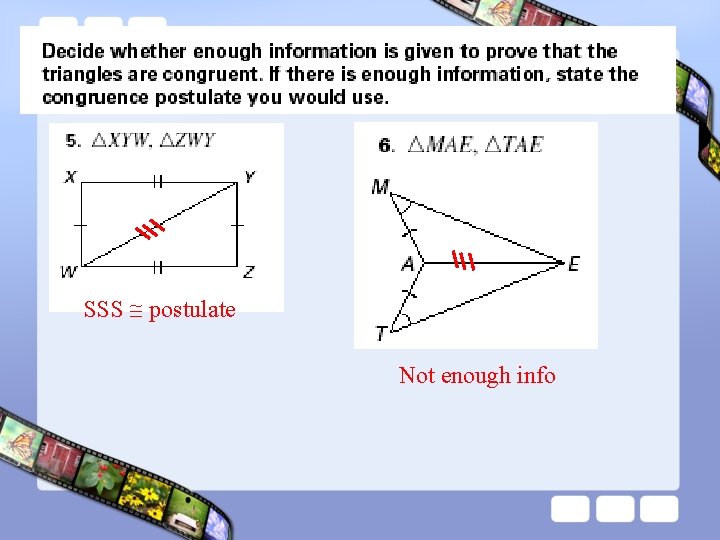
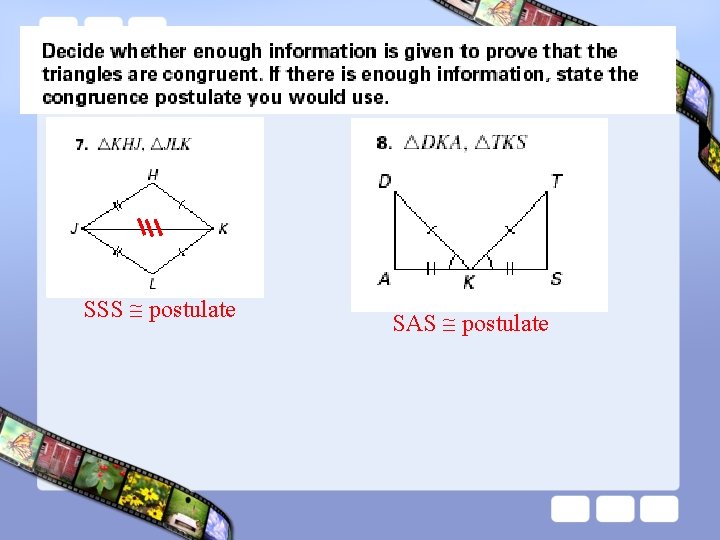
SSS postulate Not enough info

SSS postulate SAS postulate

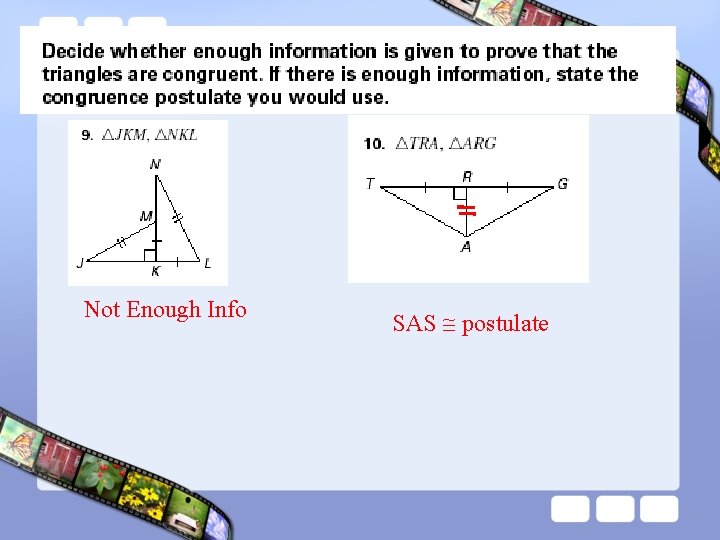
Not Enough Info SAS postulate

SSS postulate Not Enough Info

SAS postulate

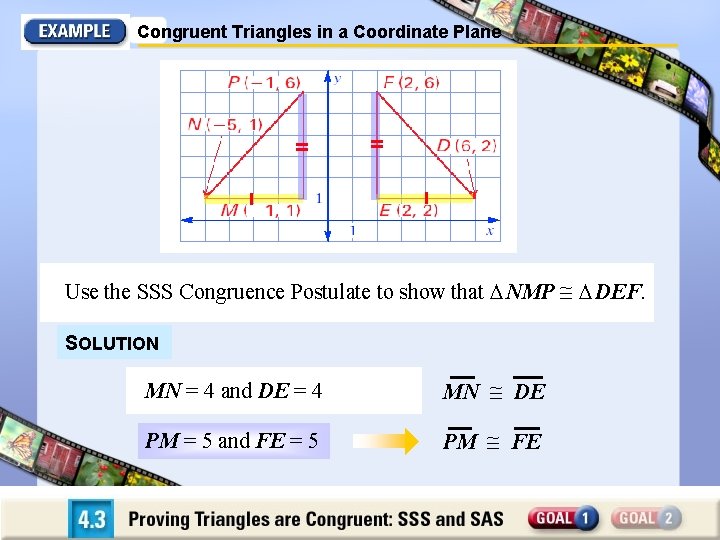
Congruent Triangles in a Coordinate Plane Use the SSS Congruence Postulate to show that NMP DEF. SOLUTION MN = 4 and DE = 4 MN DE PM = 5 and FE = 5 PM FE

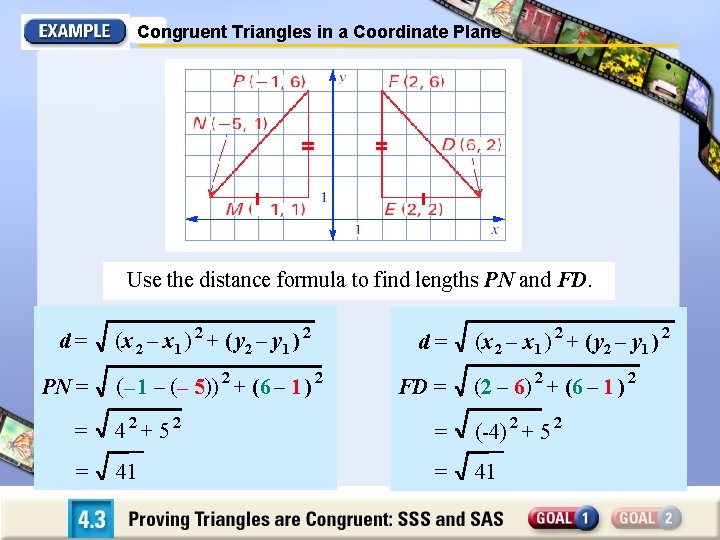
Congruent Triangles in a Coordinate Plane Use the distance formula to find lengths PN and FD. d= PN = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (– 1 – (– 5)) 2 + (6 – 1 ) 2 d= FD = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (2 – 6) 2 + (6 – 1 ) 2 = 42 + 52 = (-4) 2 + 5 2 = 41

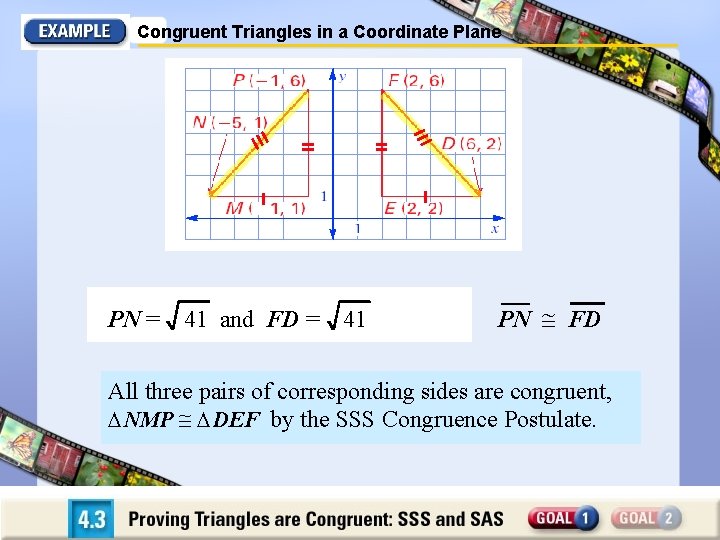
Congruent Triangles in a Coordinate Plane PN = 41 and FD = 41 PN FD All three pairs of corresponding sides are congruent, NMP DEF by the SSS Congruence Postulate.

Proving Triangles are Congruent ASA; AAS

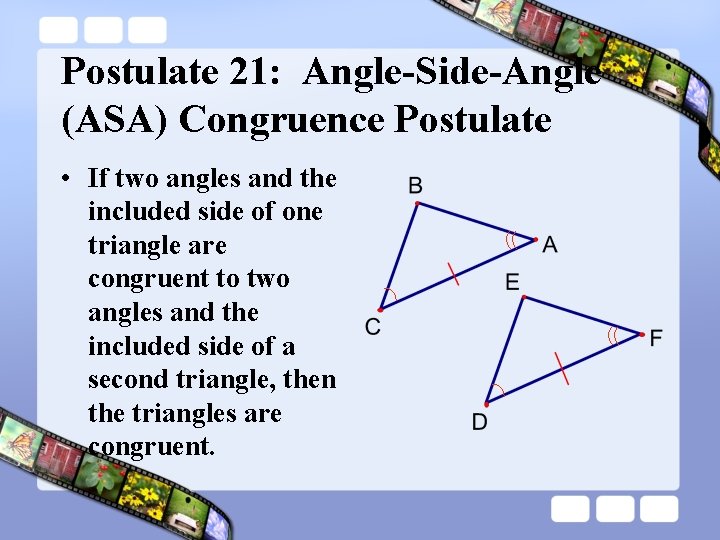
Postulate 21: Angle-Side-Angle (ASA) Congruence Postulate • If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the triangles are congruent.

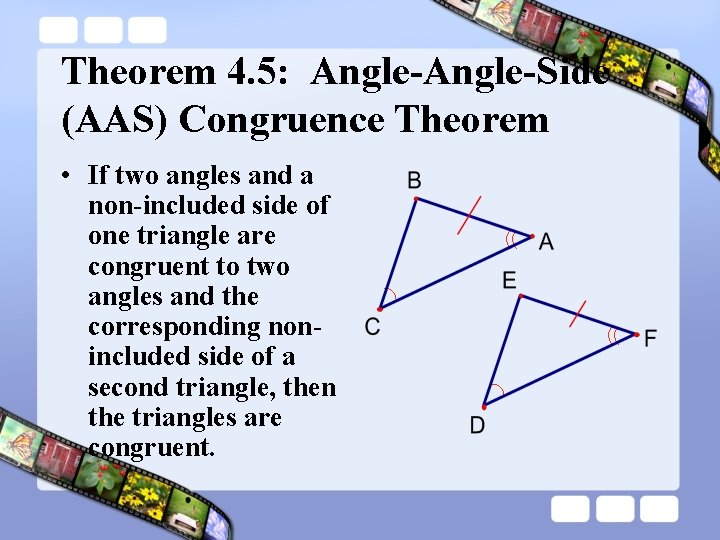
Theorem 4. 5: Angle-Side (AAS) Congruence Theorem • If two angles and a non-included side of one triangle are congruent to two angles and the corresponding nonincluded side of a second triangle, then the triangles are congruent.

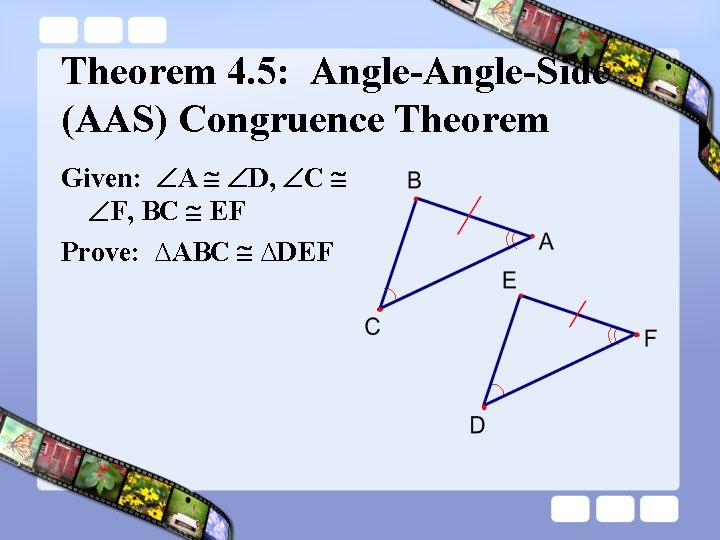
Theorem 4. 5: Angle-Side (AAS) Congruence Theorem Given: A D, C F, BC EF Prove: ∆ABC ∆DEF

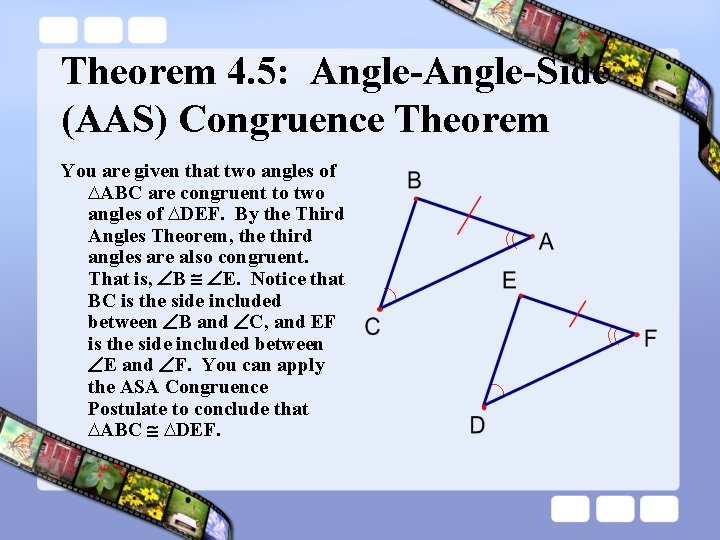
Theorem 4. 5: Angle-Side (AAS) Congruence Theorem You are given that two angles of ∆ABC are congruent to two angles of ∆DEF. By the Third Angles Theorem, the third angles are also congruent. That is, B E. Notice that BC is the side included between B and C, and EF is the side included between E and F. You can apply the ASA Congruence Postulate to conclude that ∆ABC ∆DEF.

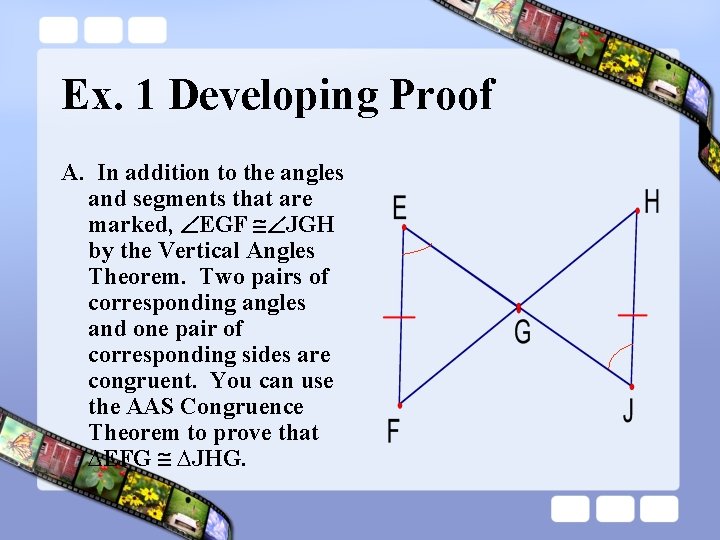
Ex. 1 Developing Proof Is it possible to prove the triangles are congruent? If so, state the postulate or theorem you would use. Explain your reasoning.

Ex. 1 Developing Proof A. In addition to the angles and segments that are marked, EGF JGH by the Vertical Angles Theorem. Two pairs of corresponding angles and one pair of corresponding sides are congruent. You can use the AAS Congruence Theorem to prove that ∆EFG ∆JHG.

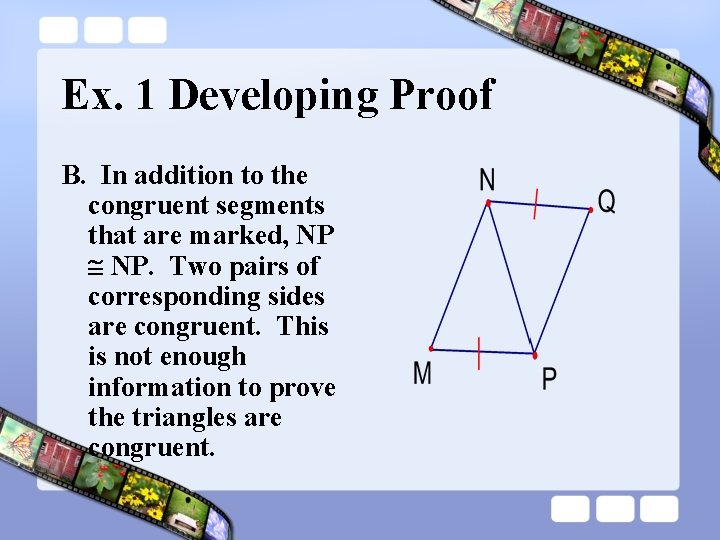
Ex. 1 Developing Proof Is it possible to prove the triangles are congruent? If so, state the postulate or theorem you would use. Explain your reasoning.

Ex. 1 Developing Proof B. In addition to the congruent segments that are marked, NP NP. Two pairs of corresponding sides are congruent. This is not enough information to prove the triangles are congruent.

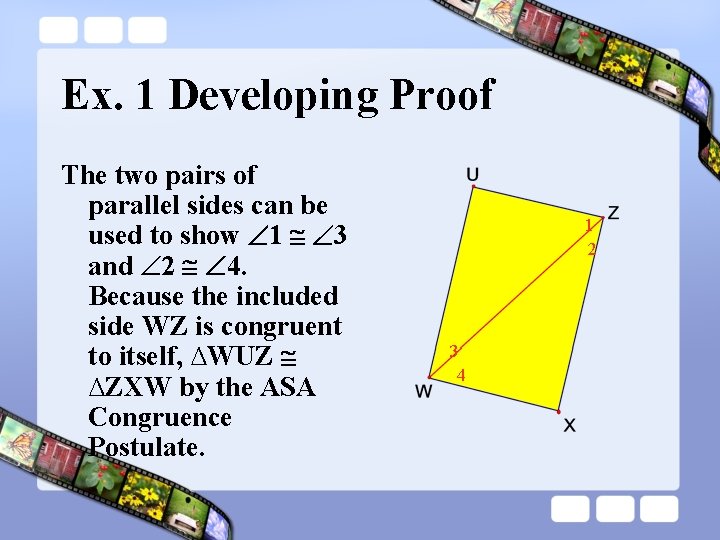
Ex. 1 Developing Proof Is it possible to prove the triangles are congruent? If so, state the postulate or theorem you would use. Explain your reasoning. UZ ║WX AND UW ║WX. 1 2 3 4

Ex. 1 Developing Proof The two pairs of parallel sides can be used to show 1 3 and 2 4. Because the included side WZ is congruent to itself, ∆WUZ ∆ZXW by the ASA Congruence Postulate. 1 2 3 4

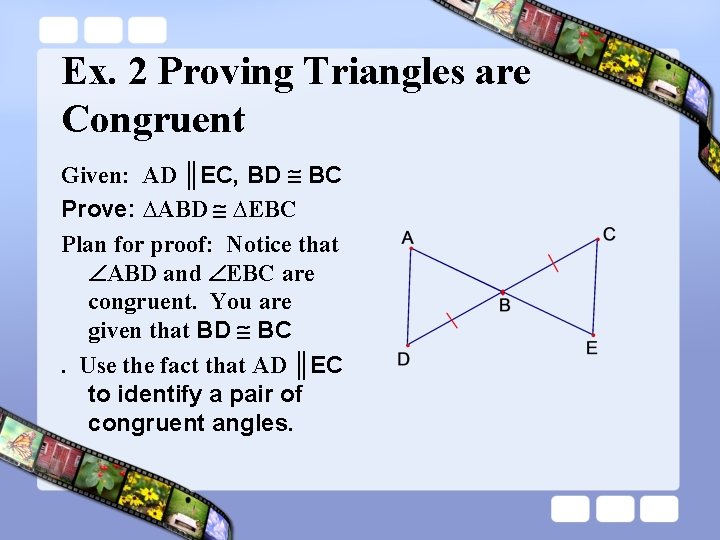
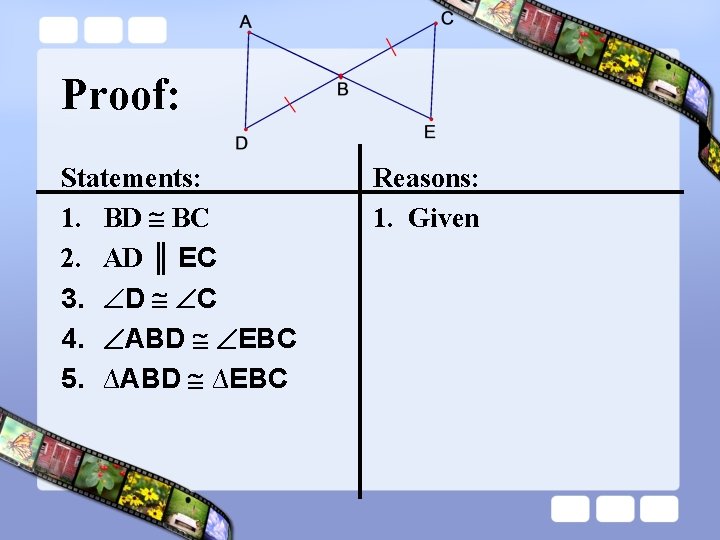
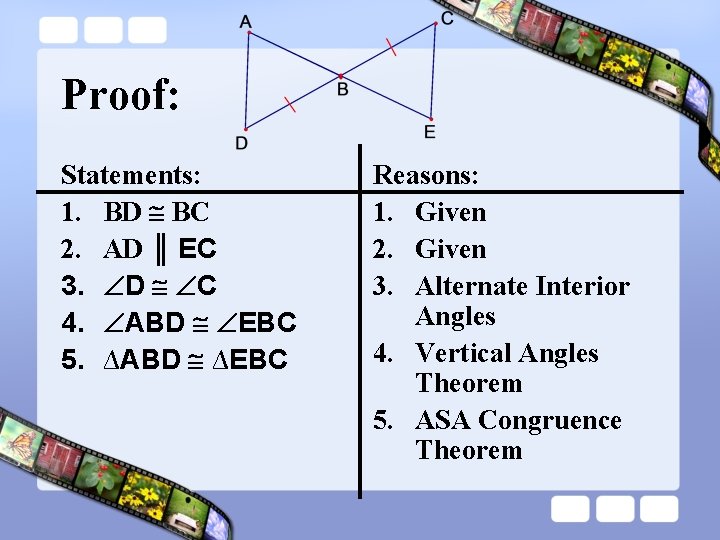
Ex. 2 Proving Triangles are Congruent Given: AD ║EC, BD BC Prove: ∆ABD ∆EBC Plan for proof: Notice that ABD and EBC are congruent. You are given that BD BC. Use the fact that AD ║EC to identify a pair of congruent angles.

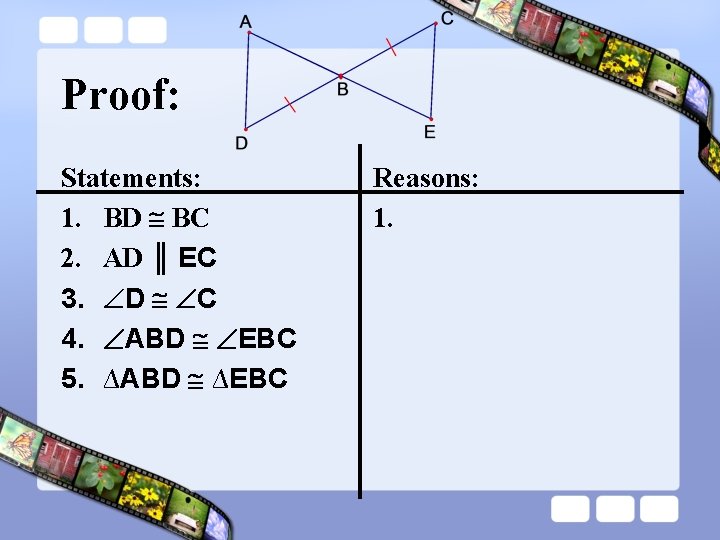
Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1.

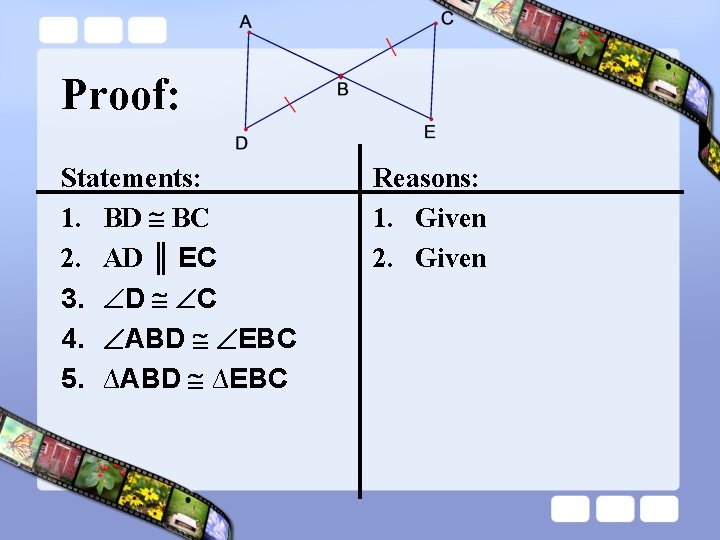
Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given

Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given 2. Given

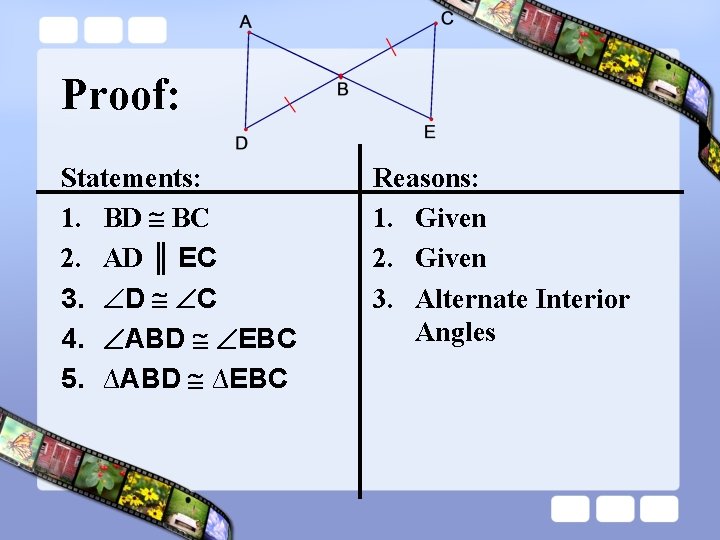
Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given 2. Given 3. Alternate Interior Angles

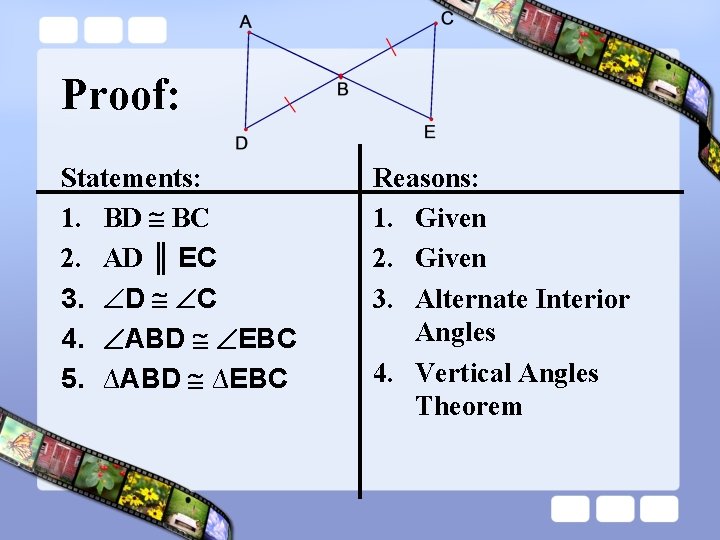
Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given 2. Given 3. Alternate Interior Angles 4. Vertical Angles Theorem

Proof: Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given 2. Given 3. Alternate Interior Angles 4. Vertical Angles Theorem 5. ASA Congruence Theorem

Note: • You can often use more than one method to prove a statement. In Example 2, you can use the parallel segments to show that D C and A E. Then you can use the AAS Congruence Theorem to prove that the triangles are congruent.