Triangle Congruence SSS SAS ASA AAS Proving Triangles




















- Slides: 55

Triangle Congruence SSS, SAS, ASA, & AAS

Proving Triangles Congruent

The Idea of a Congruence Two geometric figures with exactly the same size and shape. F B A C E D

How much do you need to know. . . about two triangles to prove that they are congruent?

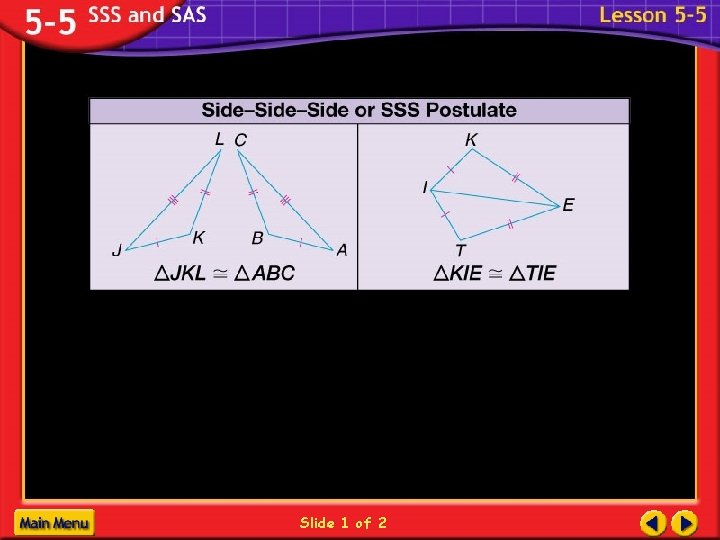
Corresponding Parts You learned that if all six pairs of corresponding parts (sides and angles) are congruent, then the triangles are congruent. B 1. AB DE 2. BC EF 3. AC DF 4. A D 5. B E 6. C F A C ABC DEF E F D

Do you need all six ? NO ! SSS SAS ASA AAS

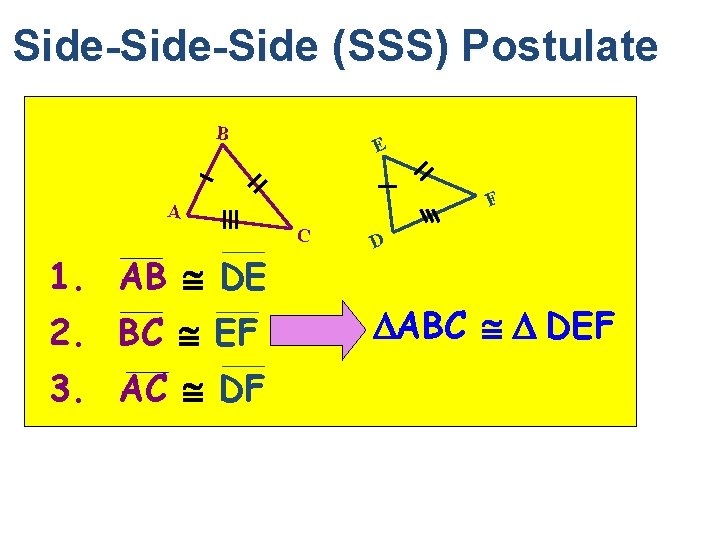
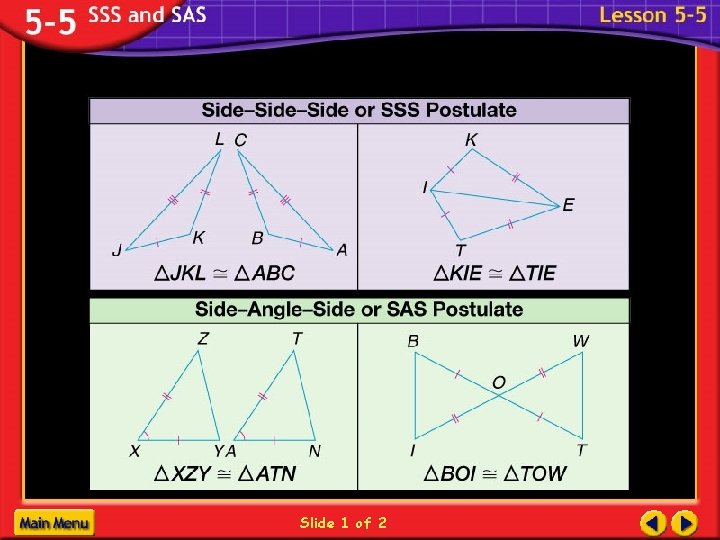
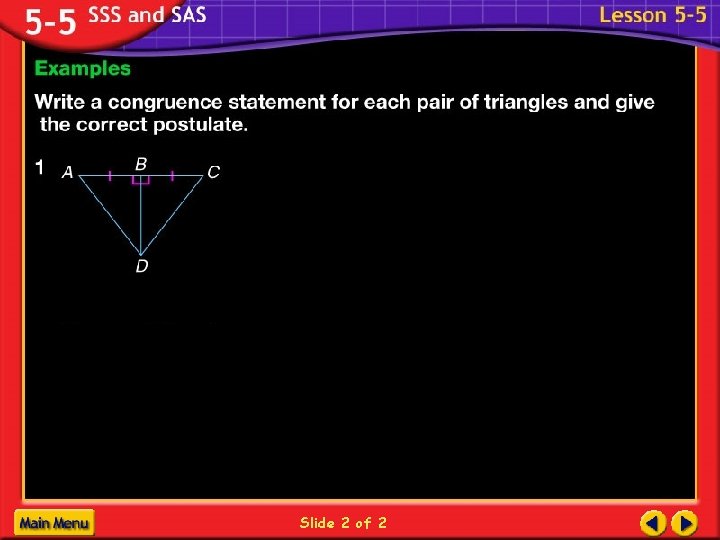
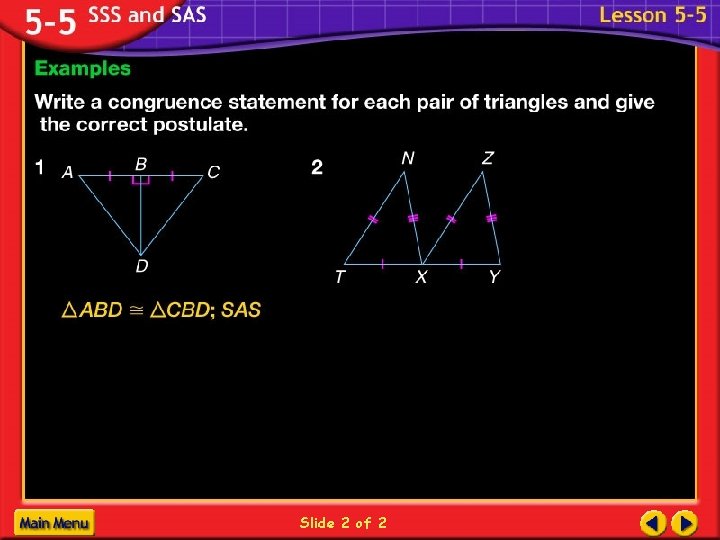
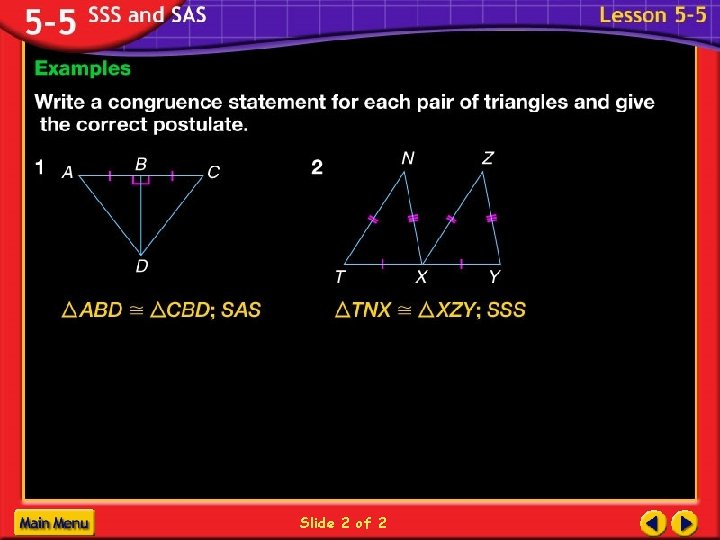
Side-Side (SSS) Postulate B E F A C 1. AB DE 2. BC EF 3. AC DF D ABC DEF

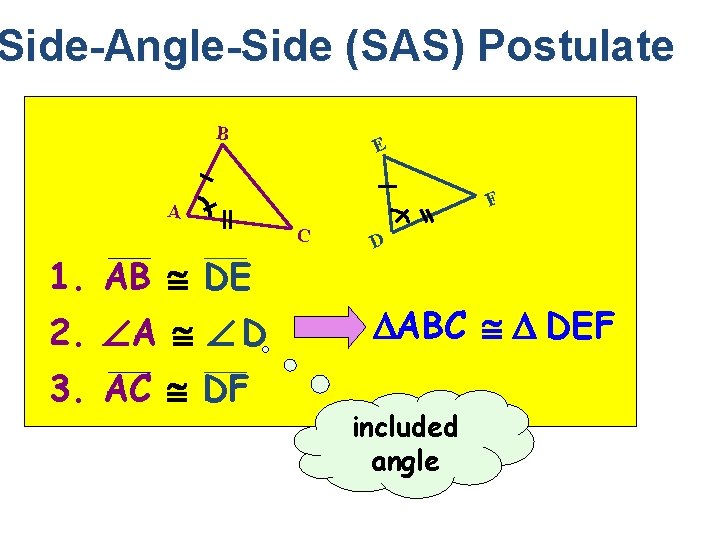
Side-Angle-Side (SAS) Postulate B E F A C 1. AB DE 2. A D 3. AC DF D ABC DEF included angle

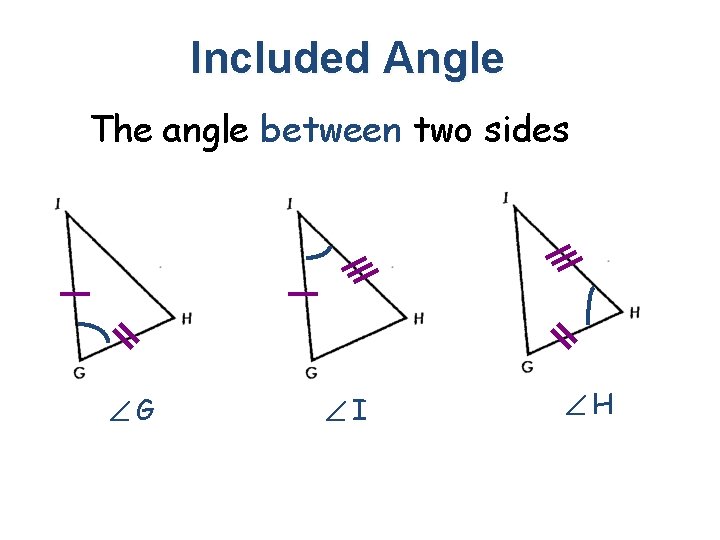
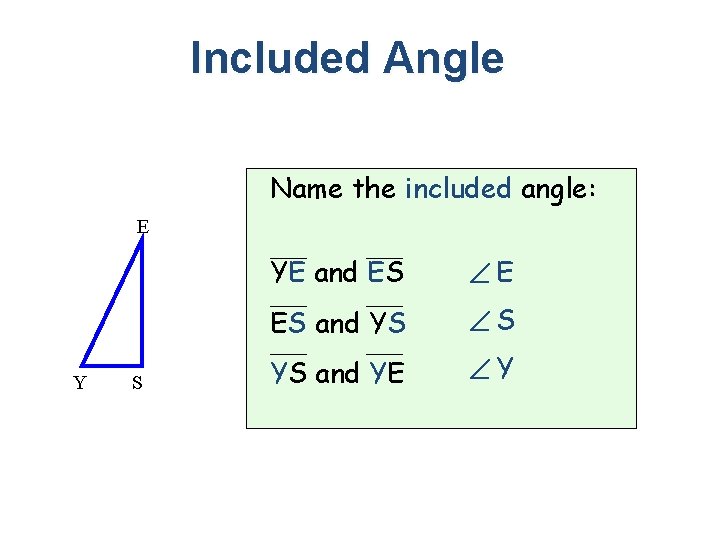
Included Angle The angle between two sides G I H

Included Angle Name the included angle: E Y S YE and ES E ES and YS S YS and YE Y

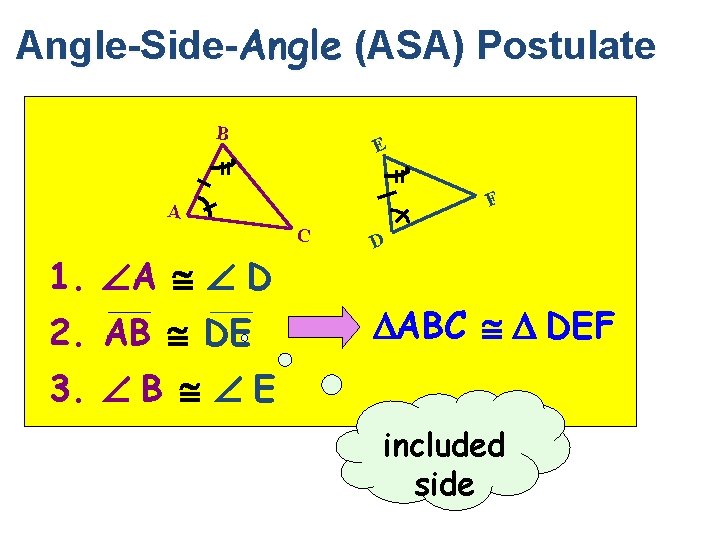
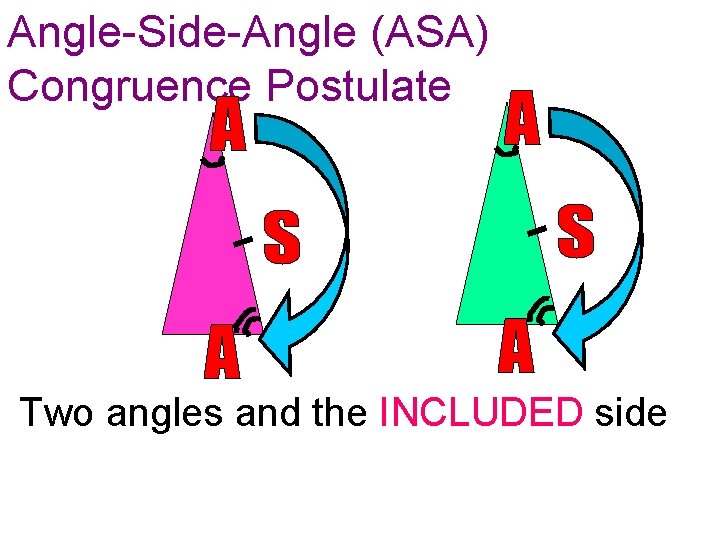
Angle-Side-Angle (ASA) Postulate B E F A C 1. A D 2. AB DE D ABC DEF 3. B E included side

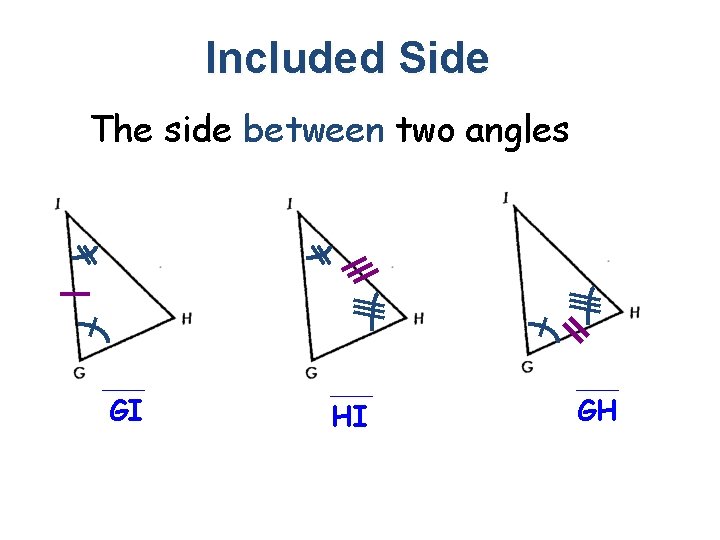
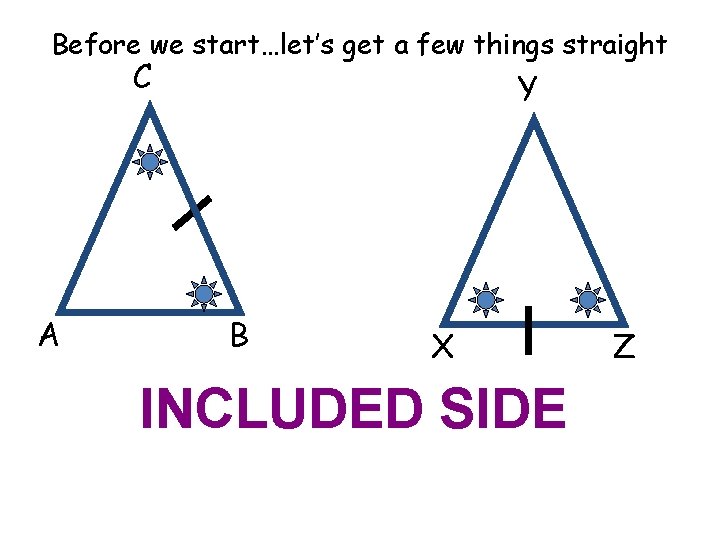
Included Side The side between two angles GI HI GH

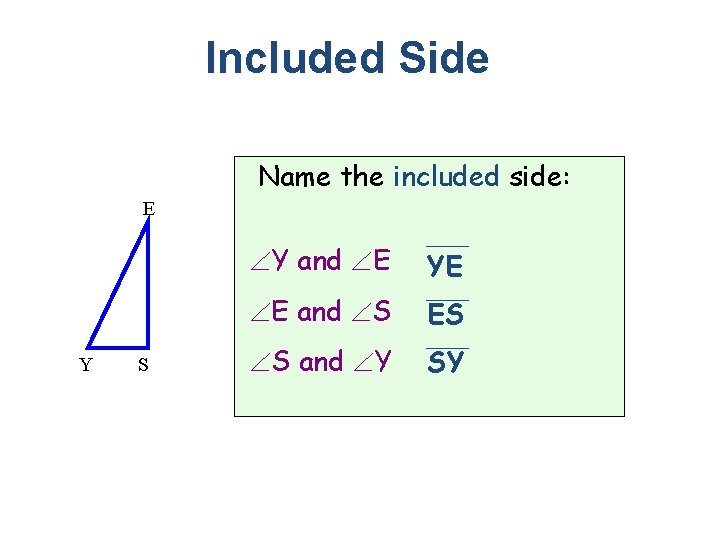
Included Side Name the included side: E Y S Y and E YE E and S ES S and Y SY

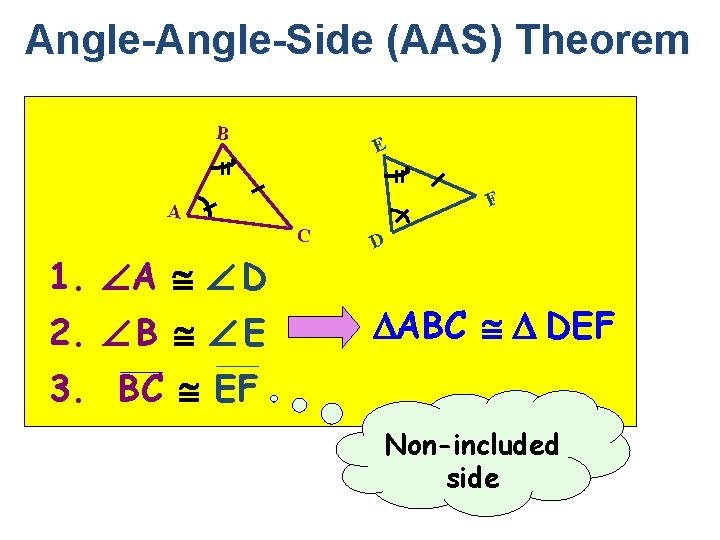
Angle-Side (AAS) Theorem B E F A C 1. A D 2. B E D ABC DEF 3. BC EF Non-included side

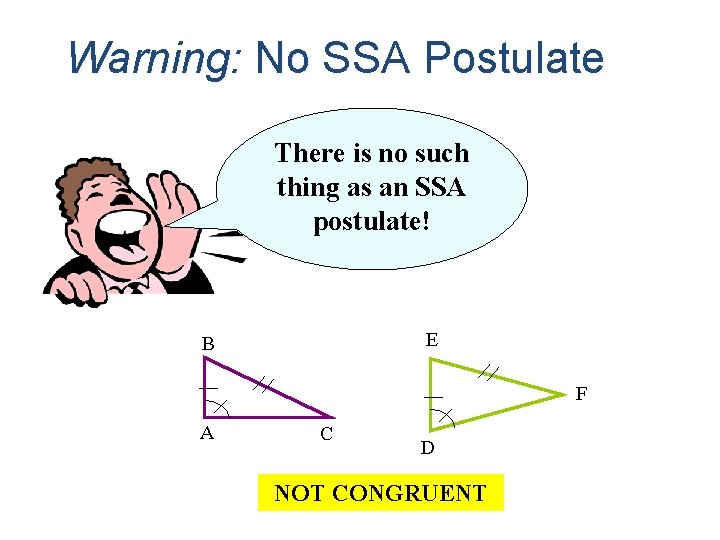
Warning: No SSA Postulate There is no such thing as an SSA postulate! E B F A C D NOT CONGRUENT

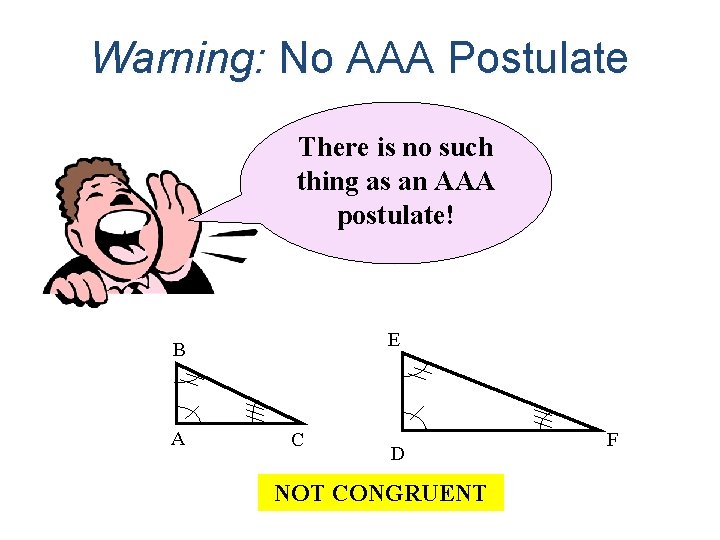
Warning: No AAA Postulate There is no such thing as an AAA postulate! E B A C D NOT CONGRUENT F

The Congruence Postulates F SSS correspondence F ASA correspondence F SAS correspondence F AAS correspondence F SSA correspondence F AAA correspondence

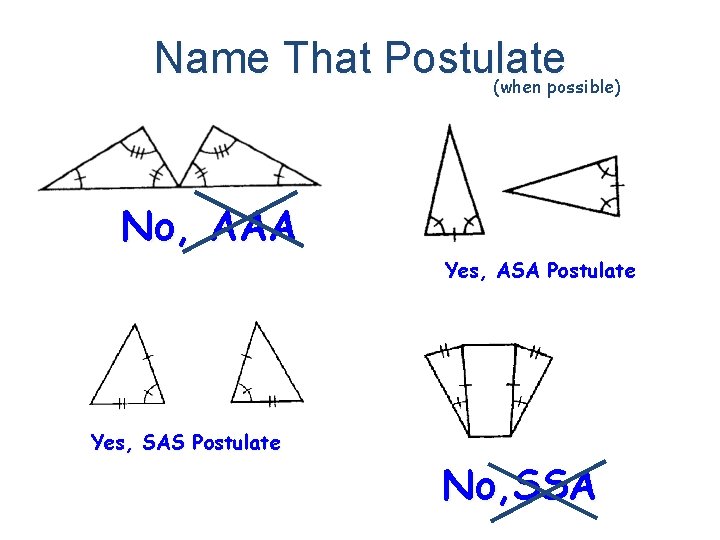
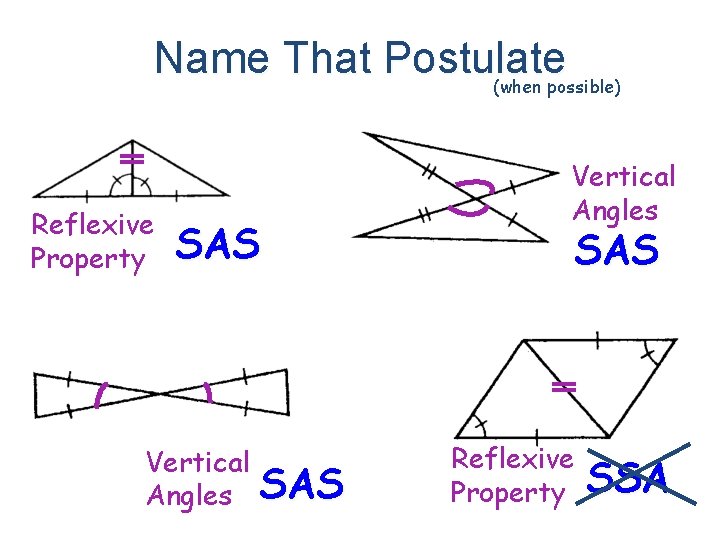
Name That Postulate (when possible) Yes, SAS Postulate No, SSA Yes, ASA Postulate Yes, SSS Postulate

Name That Postulate (when possible) No, AAA Yes, ASA Postulate Yes, SAS Postulate No, SSA

Name That Postulate (when possible) Reflexive Property SAS Vertical Angles SAS Reflexive Property SSA

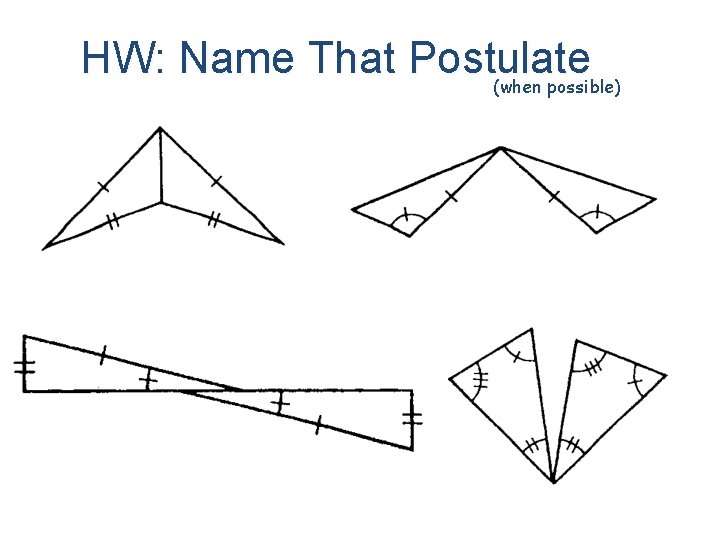
HW: Name That Postulate (when possible)

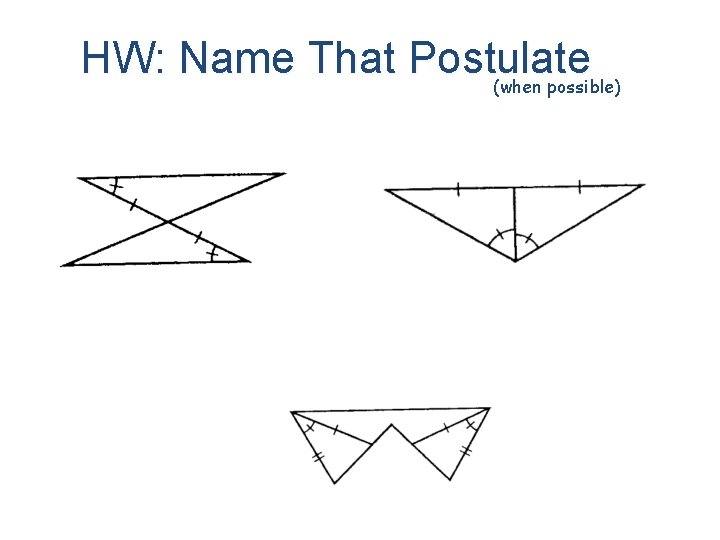
HW: Name That Postulate (when possible)

Let’s Practice Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: B D For SAS: AC FE For AAS: A F

HW Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: For SAS: For AAS:

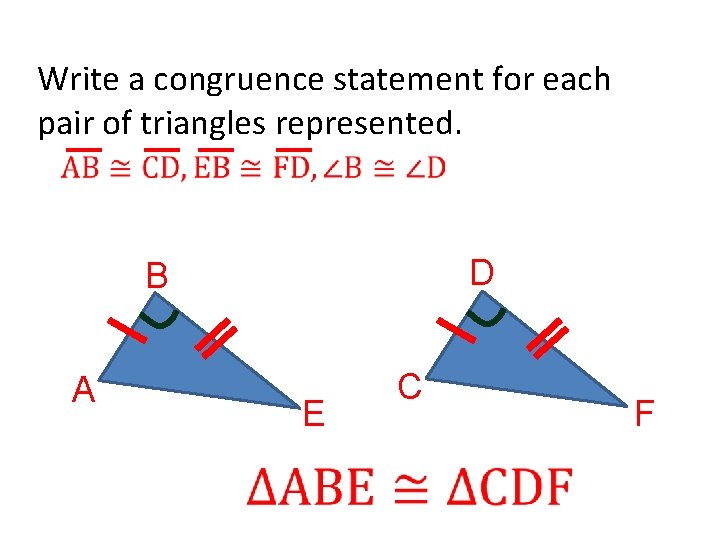
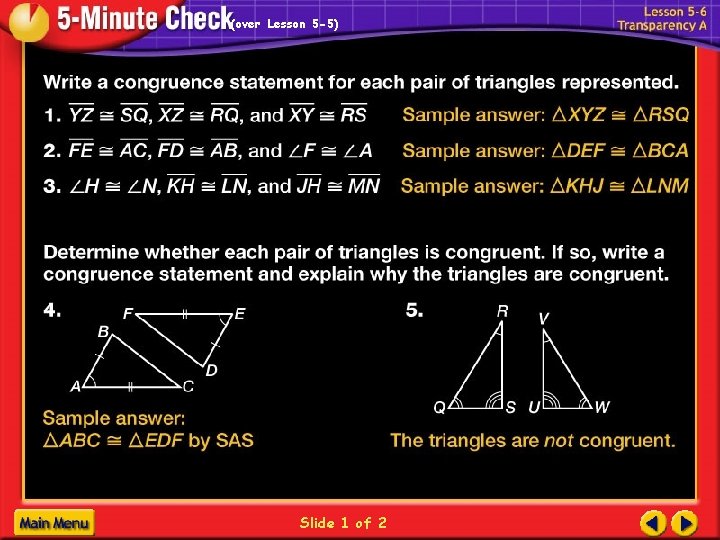
Write a congruence statement for each pair of triangles represented. D B A E C F

Slide 1 of 2

Slide 1 of 2


Before we start…let’s get a few things straight C A Y B X INCLUDED SIDE Z

Angle-Side-Angle (ASA) Congruence Postulate Two angles and the INCLUDED side

Angle-Side (AAS) Congruence Postulate Two Angles and One Side that is NOT included

Your Only Ways To Prove Triangles Are Congruent

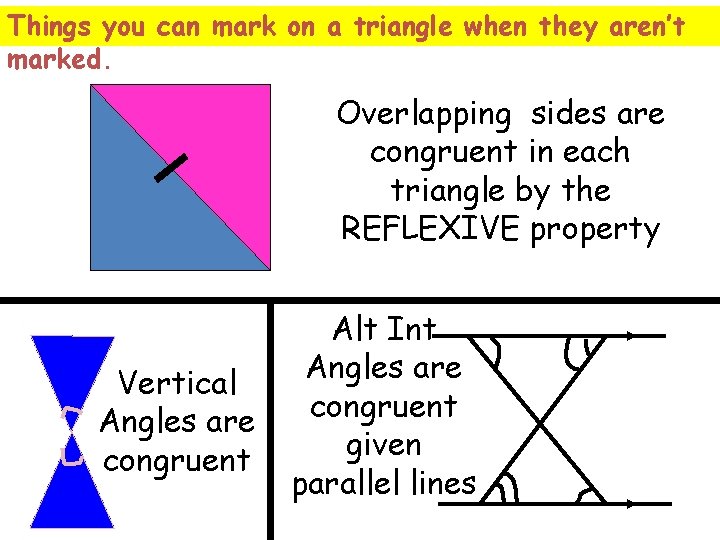
Things you can mark on a triangle when they aren’t marked. Overlapping sides are congruent in each triangle by the REFLEXIVE property Vertical Angles are congruent Alt Int Angles are congruent given parallel lines

Ex 1 DEF NLM

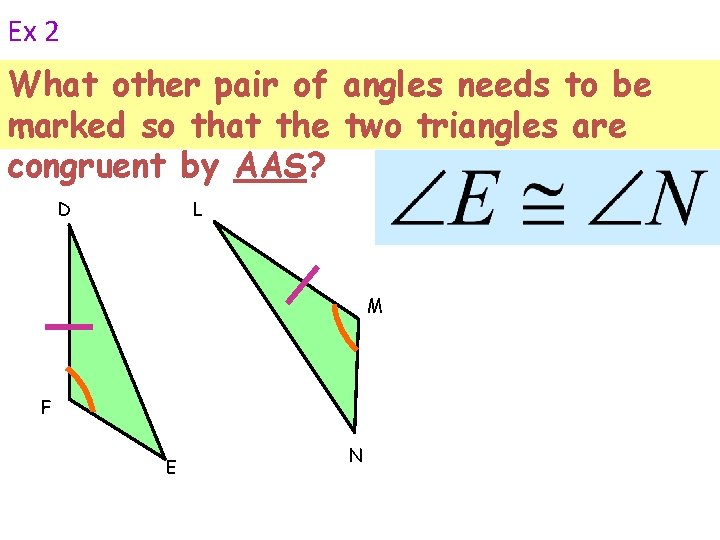
Ex 2 What other pair of angles needs to be marked so that the two triangles are congruent by AAS? D L M F E N

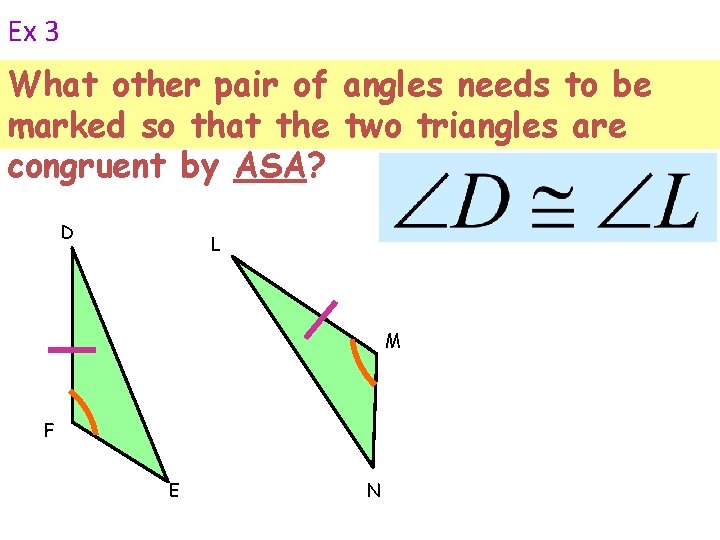
Ex 3 What other pair of angles needs to be marked so that the two triangles are congruent by ASA? D L M F E N

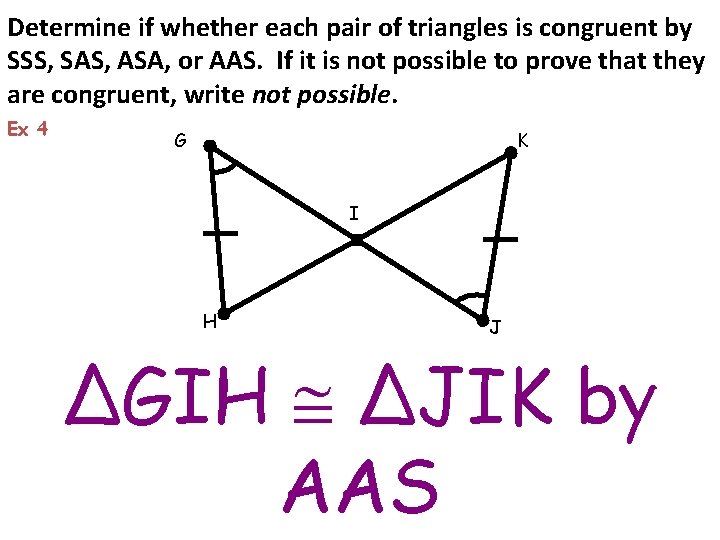
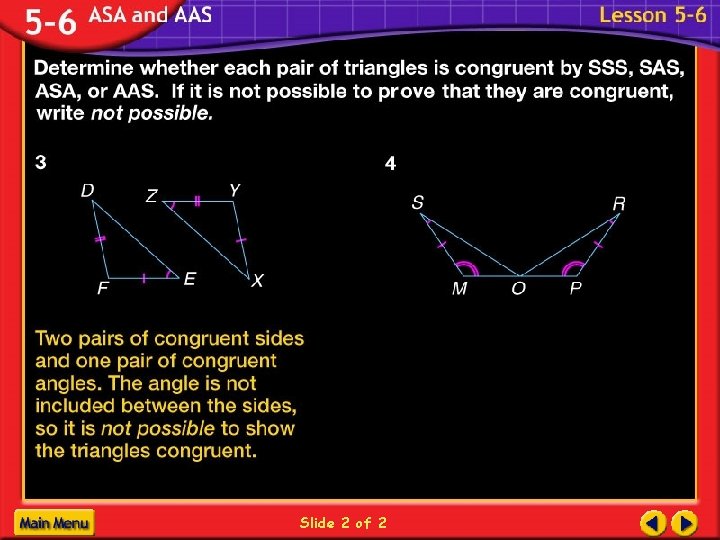
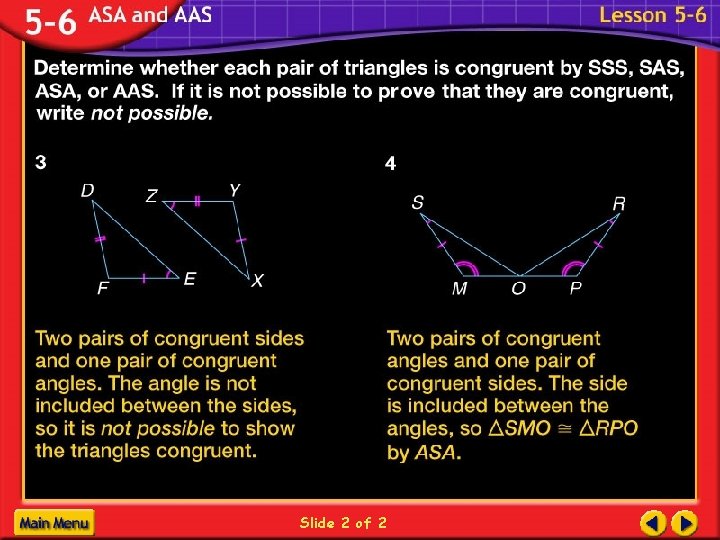
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 4 G K I H J ΔGIH ΔJIK by AAS

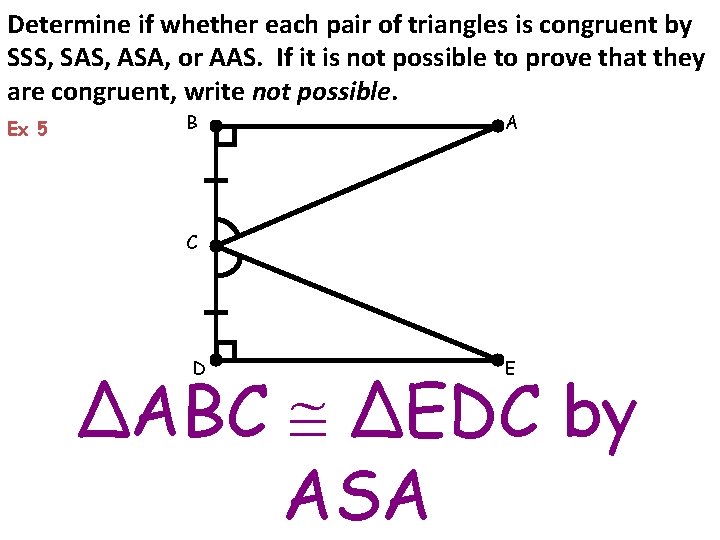
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 5 B A C D E ΔABC ΔEDC by ASA

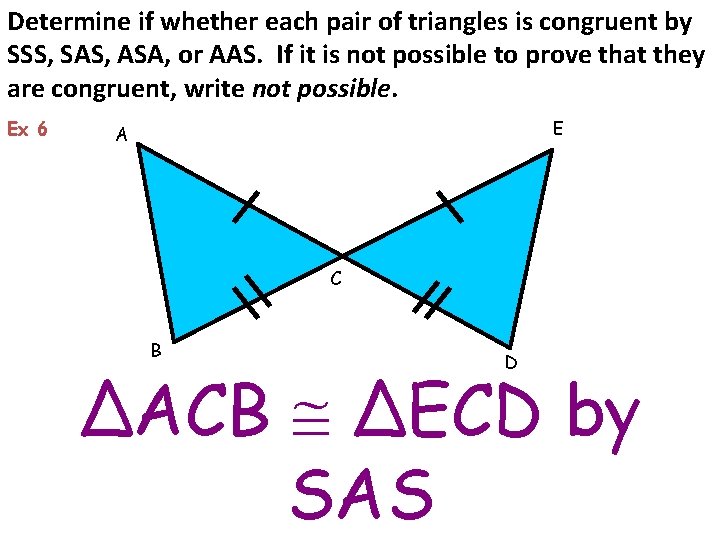
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 6 E A C B D ΔACB ΔECD by SAS

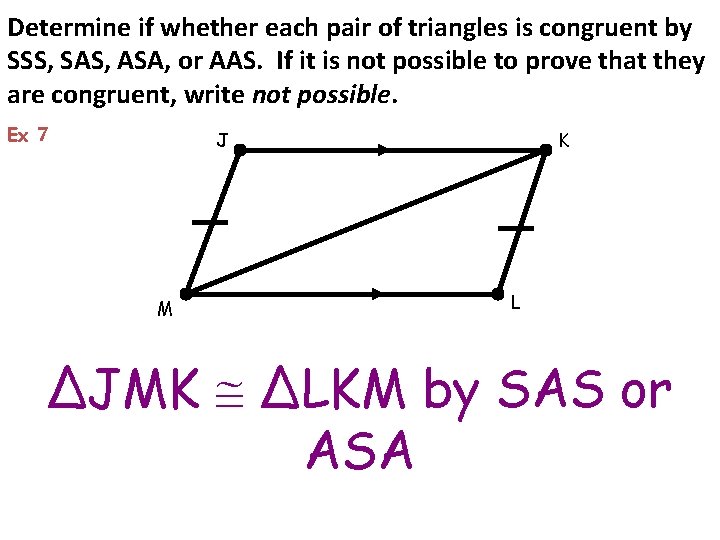
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 7 J M K L ΔJMK ΔLKM by SAS or ASA

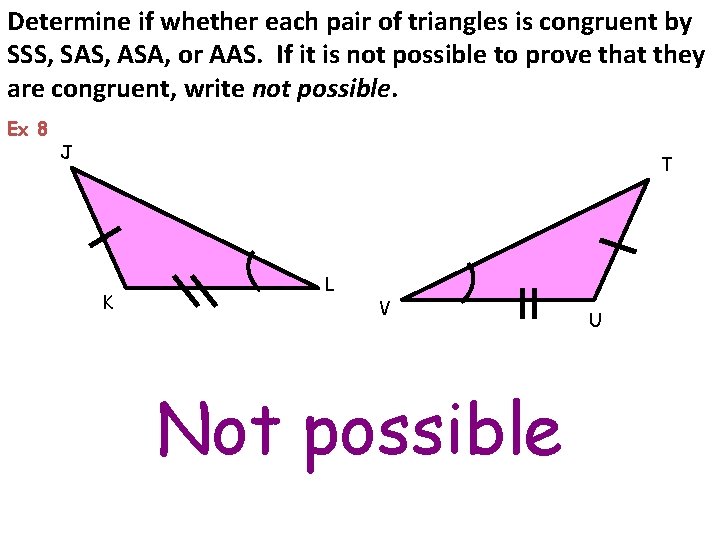
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 8 J T K L V Not possible U

Slide 2 of 2

Slide 2 of 2

Slide 2 of 2

Slide 2 of 2

(over Lesson 5 -5) Slide 1 of 2

(over Lesson 5 -5) Slide 1 of 2

Slide 1 of 2

Slide 1 of 2

Slide 1 of 2

Slide 1 of 2

Slide 2 of 2

Slide 2 of 2

Slide 2 of 2

Slide 2 of 2