Lesson 4 3 Congruent Triangles Congruent triangles triangles

Lesson 4 -3 Congruent Triangles • Congruent triangles- triangles that are the same size and shape • Definition of Congruent Triangles (CPCTC) Two triangles are congruent if and only if their corresponding sides are congruent. • Congruence transformations- when you slide, flip, or turn a triangle, the size and shapes do not change.

Lesson 4 -3 Congruent Triangles • Theorem 4. 4 Properties of Triangle Congruence • Reflexive • Symmetric • Transitive

ARCHITECTURE A tower roof is composed of congruent triangles all converging toward a point at the top. Name the corresponding congruent angles and sides of HIJ and LIK. Answer: Since corresponding parts of congruent triangles are congruent,

ARCHITECTURE A tower roof is composed of congruent triangles all converging toward a point at the top. Name the congruent triangles. Answer: HIJ LIK

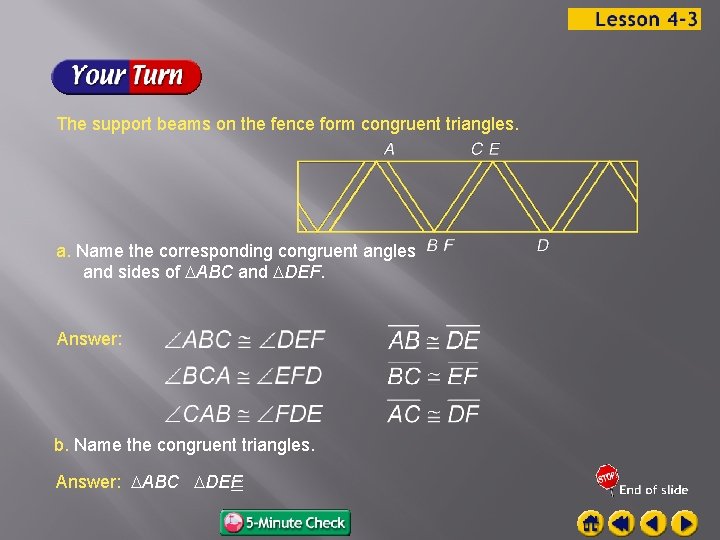
The support beams on the fence form congruent triangles. a. Name the corresponding congruent angles and sides of ABC and DEF. Answer: b. Name the congruent triangles. Answer: ABC DEF

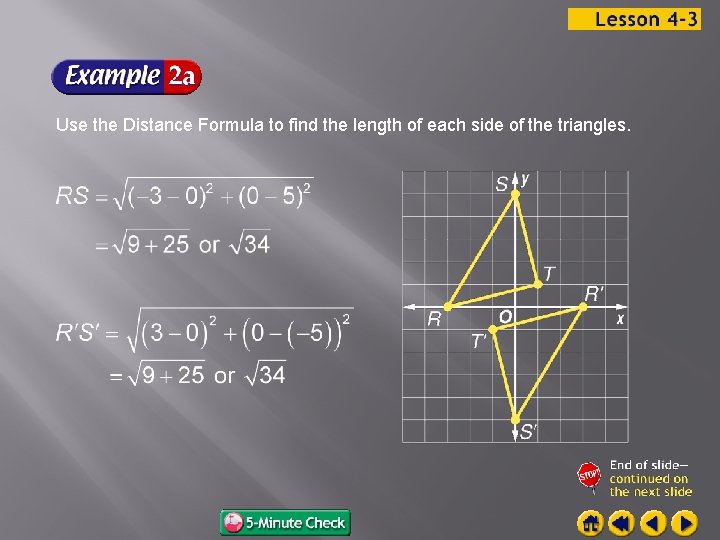
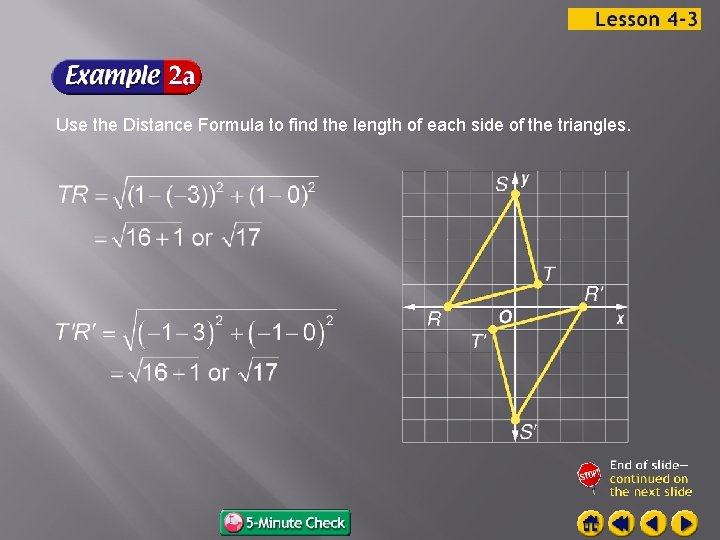
COORDINATE GEOMETRY The vertices of RST are R(─3, 0), S(0, 5), and T(1, 1). The vertices of R S T are R (3, 0), S (0, ─5), and T (─1, ─1). Verify that RST R S T.

Use the Distance Formula to find the length of each side of the triangles.

Use the Distance Formula to find the length of each side of the triangles.

Use the Distance Formula to find the length of each side of the triangles.

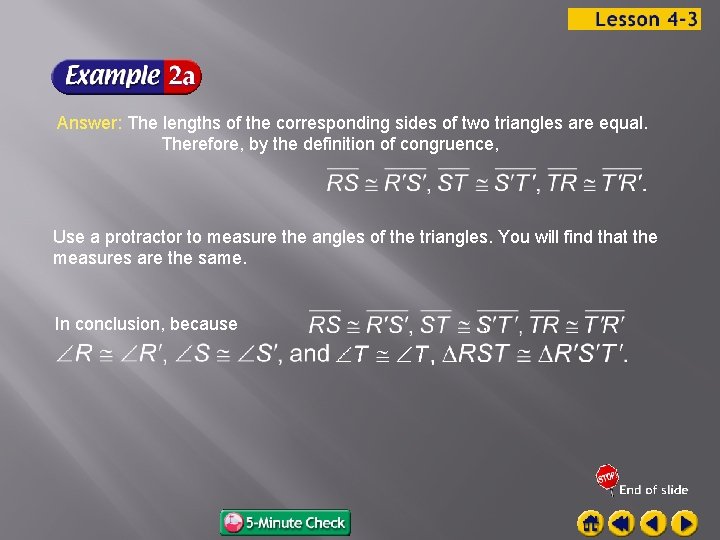
Answer: The lengths of the corresponding sides of two triangles are equal. Therefore, by the definition of congruence, Use a protractor to measure the angles of the triangles. You will find that the measures are the same. In conclusion, because ,

COORDINATE GEOMETRY The vertices of RST are R(─3, 0), S(0, 5), and T(1, 1). The vertices of R S T are R (3, 0), S (0, ─5), and T (─1, ─1). Name the congruence transformation for RST and R S T. Answer: R S T is a turn of RST.

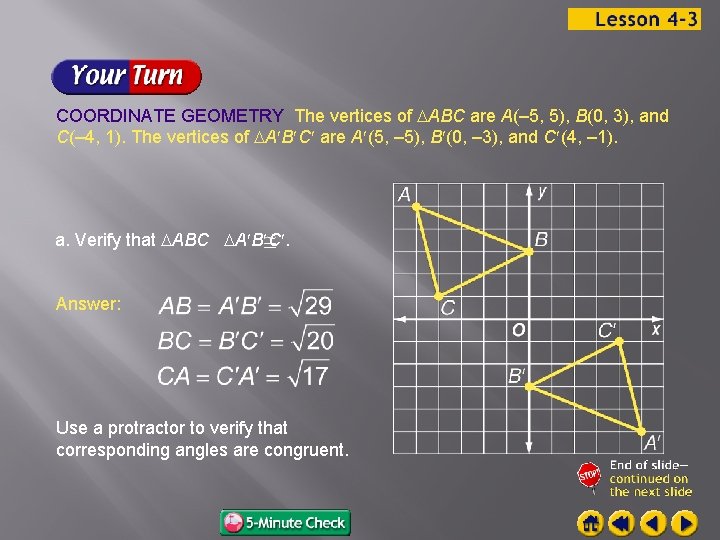
COORDINATE GEOMETRY The vertices of ABC are A(– 5, 5), B(0, 3), and C(– 4, 1). The vertices of A B C are A (5, – 5), B (0, – 3), and C (4, – 1). a. Verify that ABC A B C. Answer: Use a protractor to verify that corresponding angles are congruent.

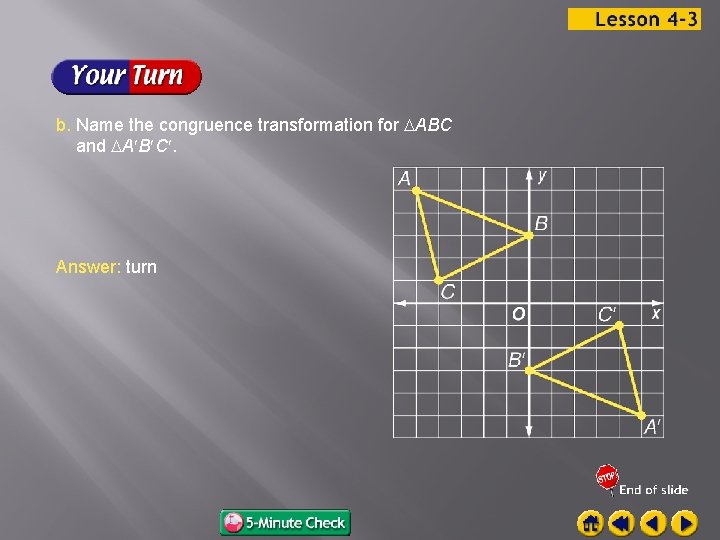
b. Name the congruence transformation for ABC and A B C. Answer: turn