Proving Triangles Congruent Triangle Congruency ShortCuts If you

Proving Triangles Congruent

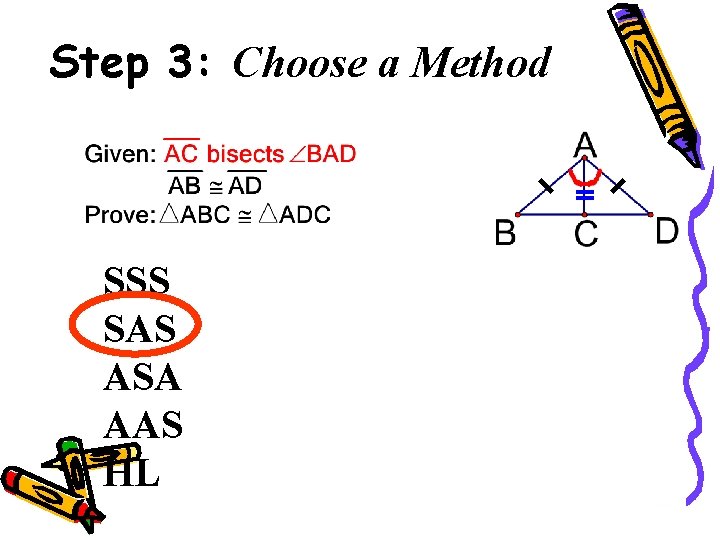
Triangle Congruency Short-Cuts If you can prove one of the following short cuts, you have two congruent triangles 1. 2. 3. 4. 5. SSS (side-side) SAS (side-angle-side) ASA (angle-side-angle) AAS (angle-side) HL (hypotenuse-leg) right triangles only!

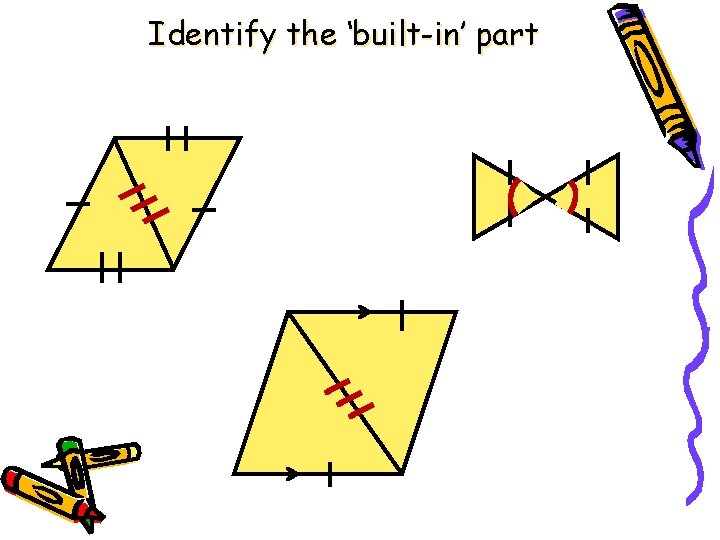
Built – In Information in Triangles •

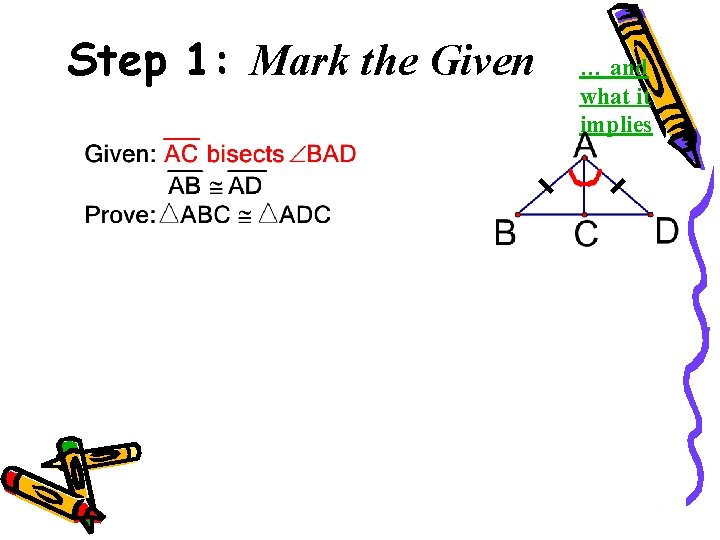
Identify the ‘built-in’ part

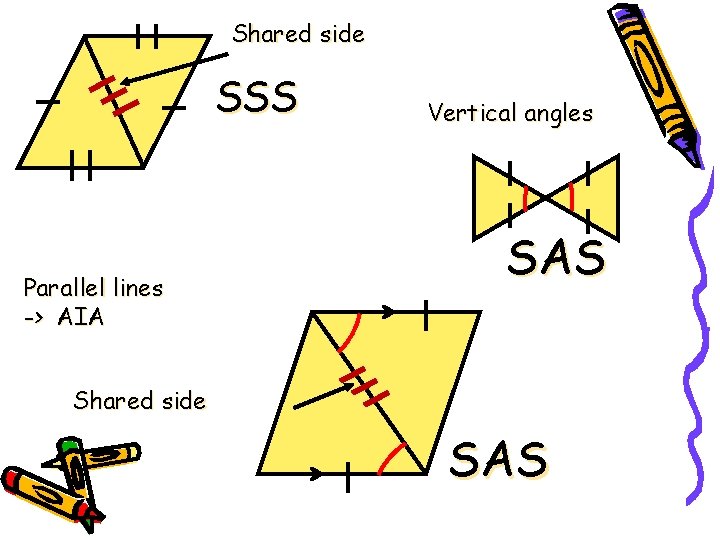
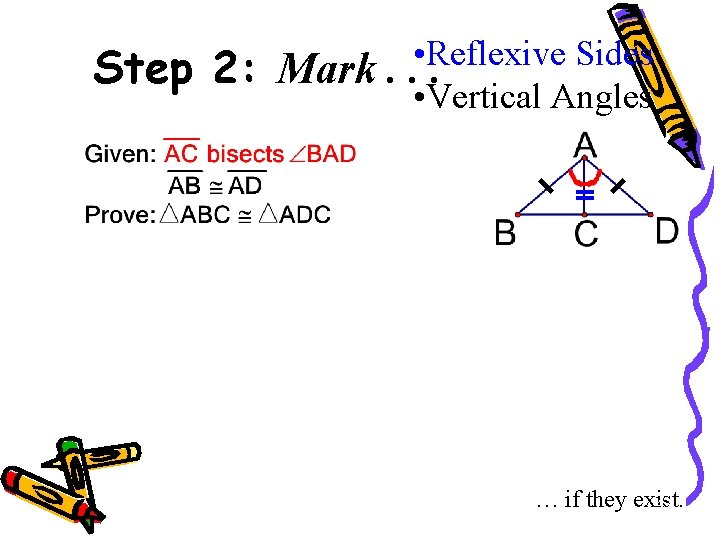
Shared side SSS Parallel lines -> AIA Vertical angles SAS Shared side SAS

SOME REASONS For Indirect Information • • Def of midpoint Def of a bisector Vert angles are congruent Def of perpendicular bisector Reflexive property (shared side) Parallel lines …. . alt int angles Property of Perpendicular Lines

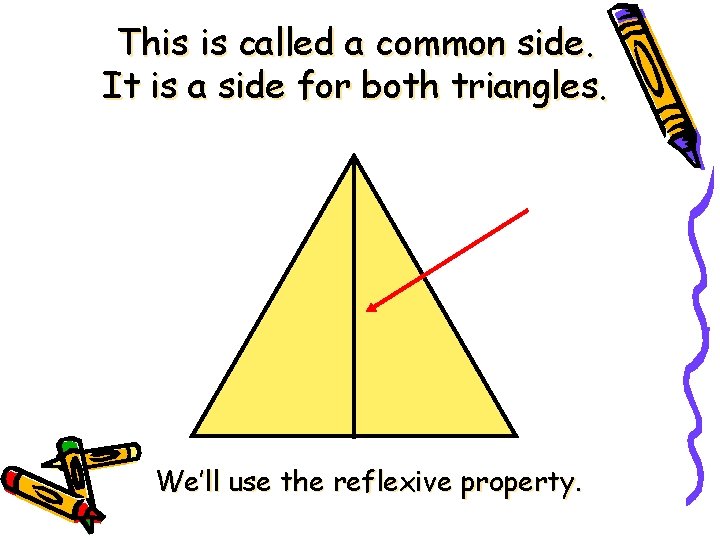
This is called a common side. It is a side for both triangles. We’ll use the reflexive property.

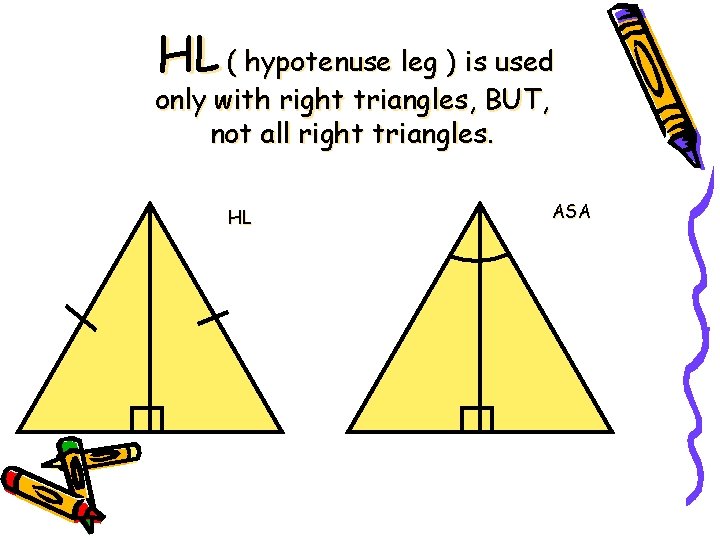
HL ( hypotenuse leg ) is used only with right triangles, BUT, not all right triangles. HL ASA

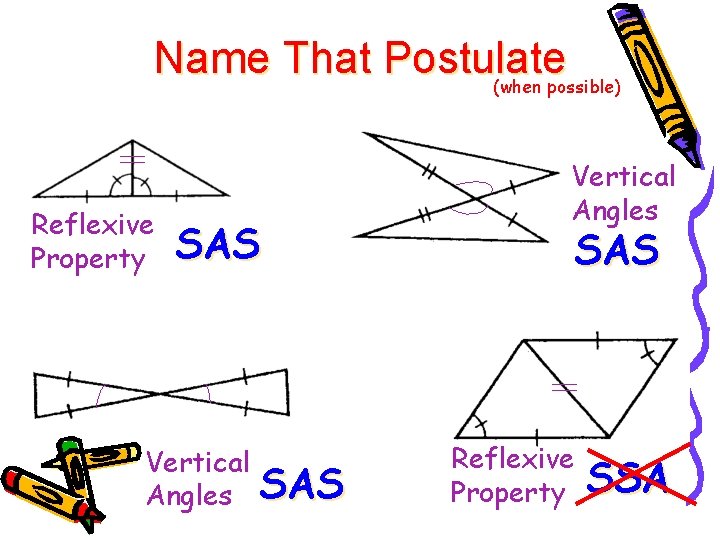
Name That Postulate (when possible) Reflexive Property SAS Vertical Angles SAS Reflexive Property SSA

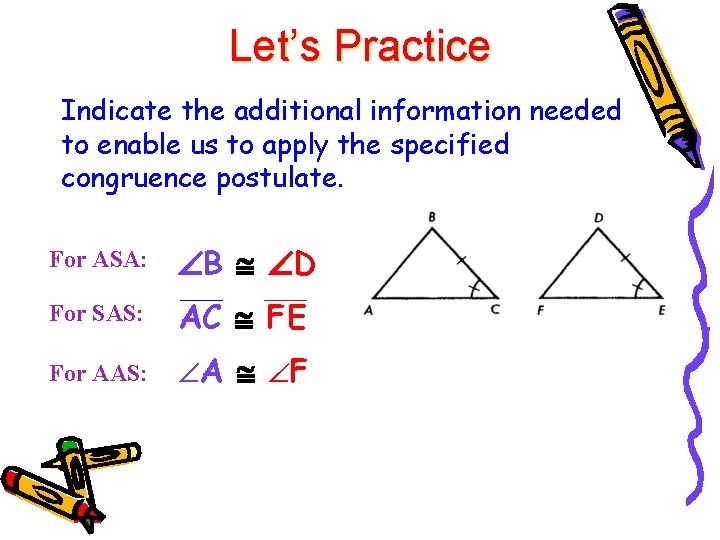
Let’s Practice Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: B D For SAS: AC FE For AAS: A F

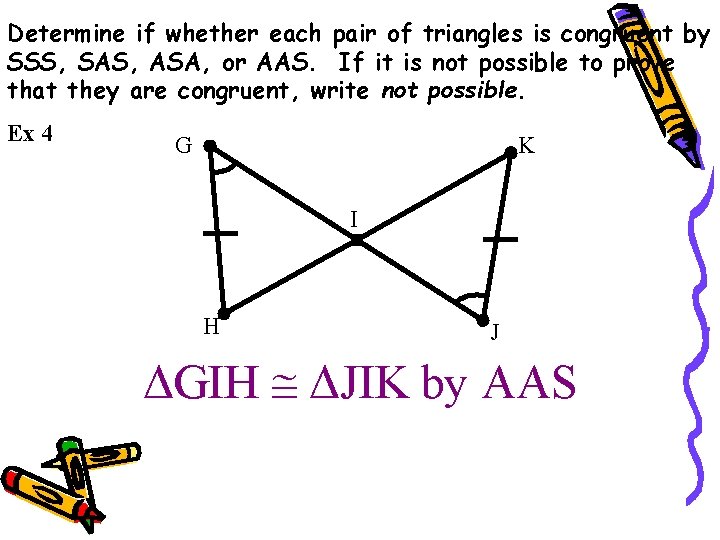
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 4 G K I H J ΔGIH ΔJIK by AAS

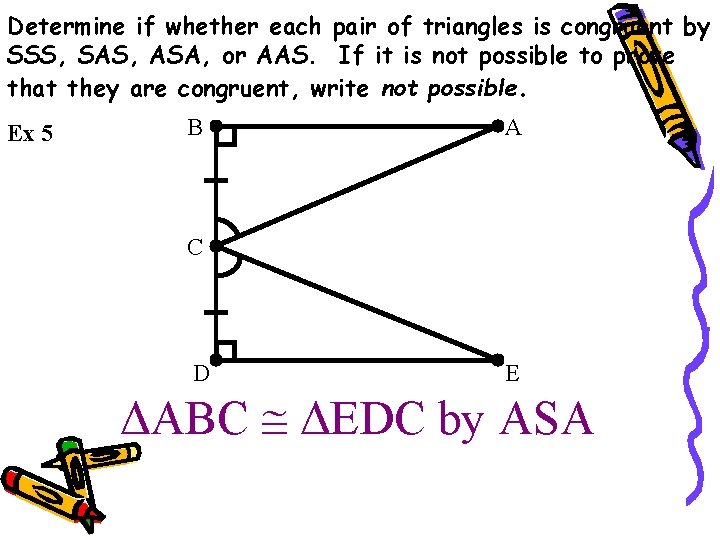
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 5 B A C D E ΔABC ΔEDC by ASA

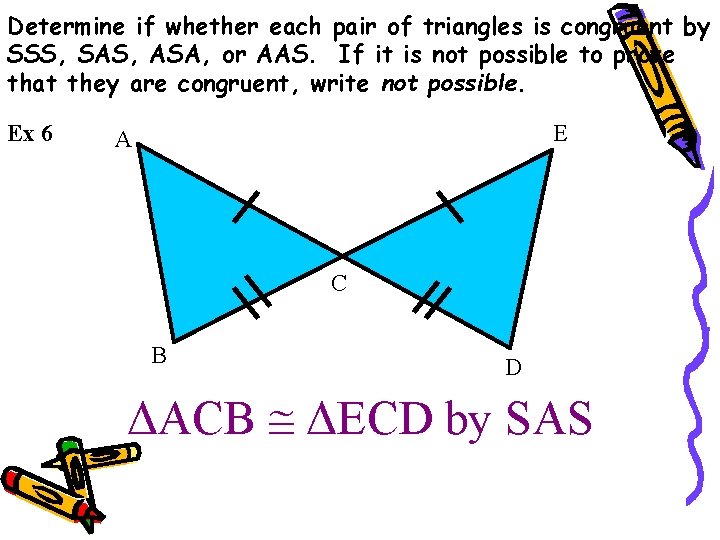
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 6 E A C B D ΔACB ΔECD by SAS

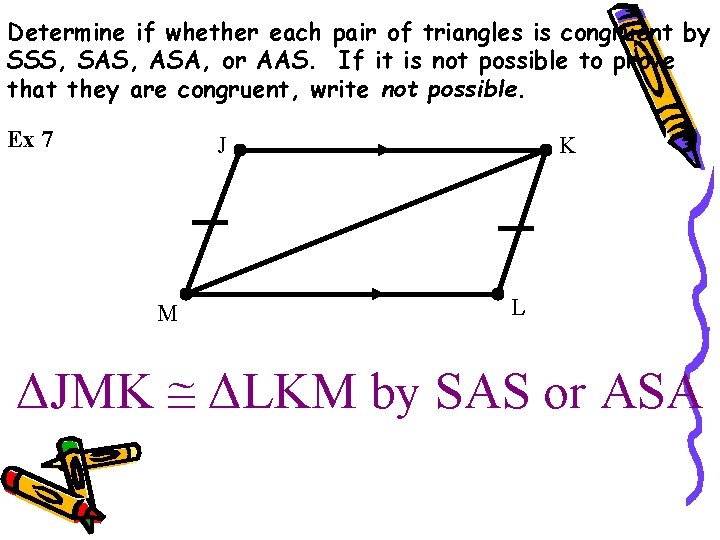
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 7 J M K L ΔJMK ΔLKM by SAS or ASA

Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. J T Ex 8 K L V Not possible U

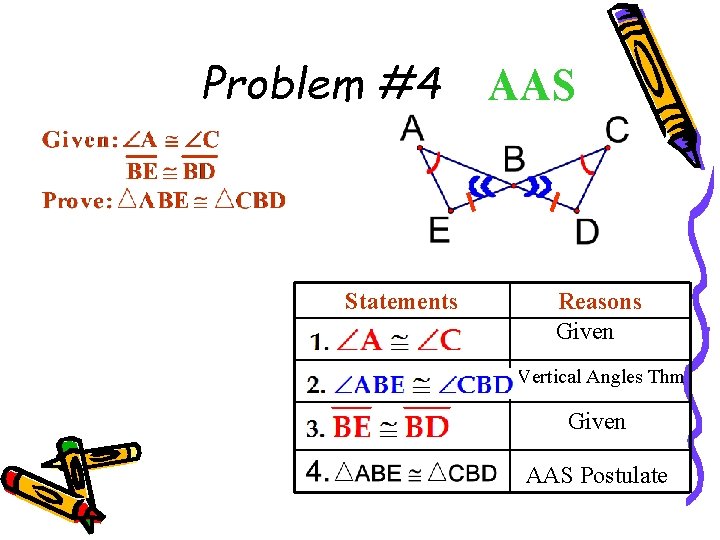
Problem #4 Statements AAS Reasons Given Vertical Angles Thm Given AAS Postulate 37

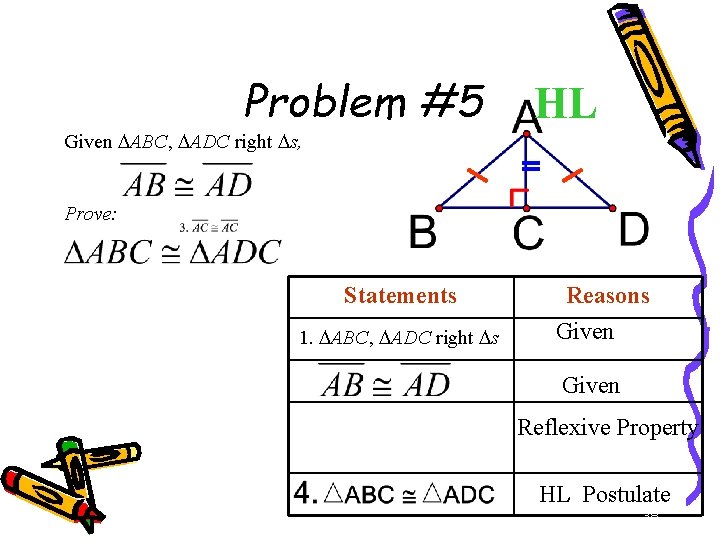
Problem #5 Given ABC, ADC right s, HL Prove: Statements 1. ABC, ADC right s Reasons Given Reflexive Property HL Postulate 38

Congruence Proofs 1. Mark the Given. 2. Mark … Reflexive Sides or Angles / Vertical Angles Also: mark info implied by given info. 3. Choose a Method. (SSS , SAS, ASA) 4. List the Parts … in the order of the method. 5. Fill in the Reasons … why you marked the parts. 6. Is there more? 39

Given implies Congruent Parts midpoint parallel segment bisector segments angles segments angle bisector angles perpendicular angles 40

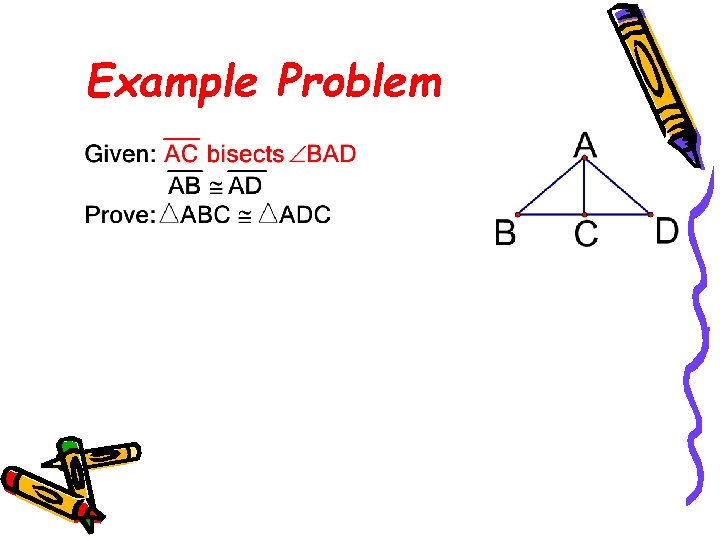
Example Problem 41

Step 1: Mark the Given … and what it implies 42

Step 2: Mark. • Reflexive Sides. . • Vertical Angles … if they exist. 43

Step 3: Choose a Method SSS SAS ASA AAS HL 44

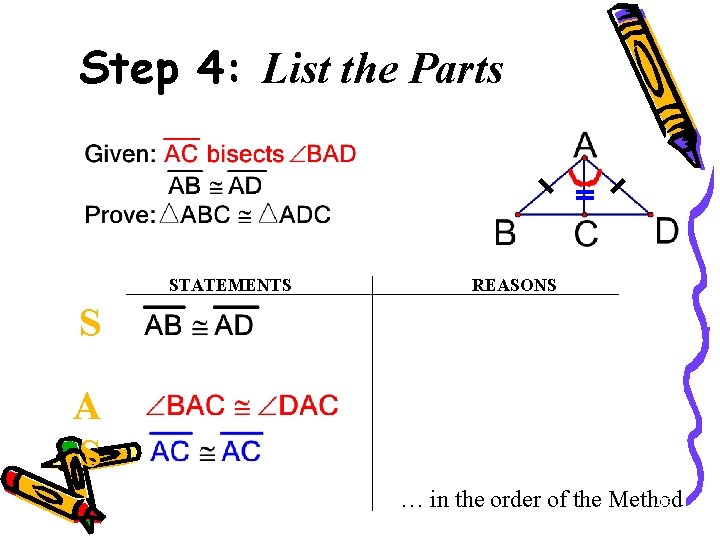
Step 4: List the Parts STATEMENTS REASONS S A S … in the order of the Method 45

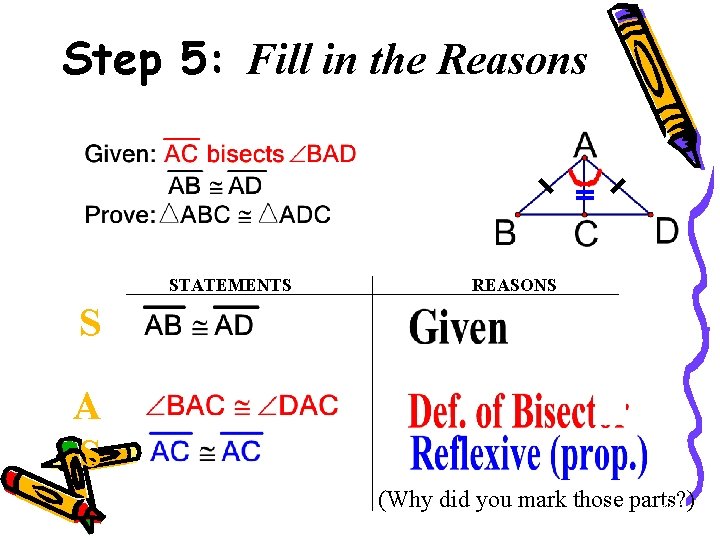
Step 5: Fill in the Reasons STATEMENTS REASONS S A S (Why did you mark those parts? ) 46

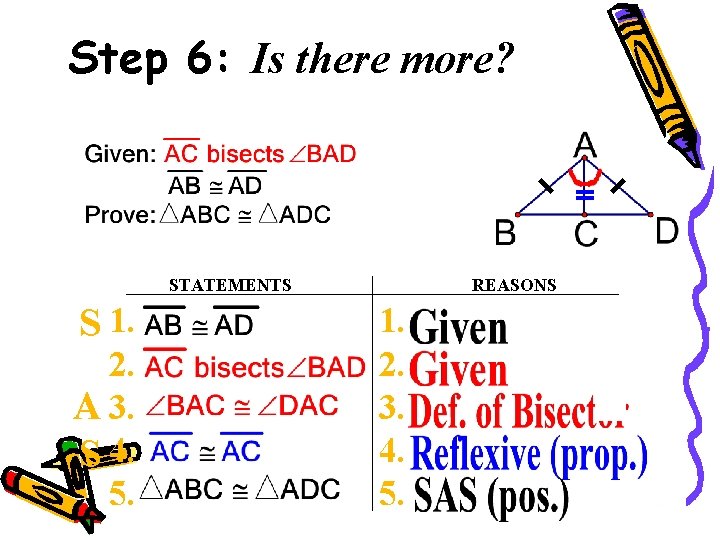
Step 6: Is there more? STATEMENTS S 1. 2. A 3. S 4. 5. REASONS 1. 2. 3. 4. 5. 47

Congruent Triangles Proofs 1. Mark the Given and what it implies. 2. Mark … Reflexive Sides / Vertical Angles 3. Choose a Method. (SSS , SAS, ASA) 4. List the Parts … in the order of the method. 5. Fill in the Reasons … why you marked the parts. 6. Is there more? 53

Using CPCTC in Proofs • According to the definition of congruence, if two triangles are congruent, their corresponding parts (sides and angles) are also congruent. • This means that two sides or angles that are not marked as congruent can be proven to be congruent if they are part of two congruent triangles. • This reasoning, when used to prove congruence, is abbreviated CPCTC, which stands for Corresponding Parts of Congruent Triangles are Congruent. 54

Corresponding Parts of Congruent Triangles • For example, can you prove that sides AD and BC are congruent in the figure at right? • The sides will be congruent if triangle ADM is congruent to triangle BCM. – Angles A and B are congruent because they are marked. – Sides MA and MB are congruent because they are marked. – Angles 1 and 2 are congruent because they are vertical angles. – So triangle ADM is congruent to triangle BCM by ASA. • This means sides AD and BC are congruent by CPCTC. 55

Corresponding Parts of Congruent Triangles • A two column proof that sides AD and BC are congruent in the figure at right is shown below: Statement Reason MA @ MB Given ÐA @ ÐB Given Ð 1 @ Ð 2 Vertical angles DADM @ DBCM ASA AD @ BC CPCTC 56

Corresponding Parts of Congruent Triangles • A two column proof that sides AD and BC are congruent in the figure at right is. Reason shown below: Statement MA @ MB Given ÐA @ ÐB Given Ð 1 @ Ð 2 Vertical angles DADM @ DBCM ASA AD @ BC CPCTC 57

Corresponding Parts of Congruent Triangles • Sometimes it is necessary to add an auxiliary line in order to complete a proof Statement Reason • For example, to prove ÐR @ ÐO in @ FO Given this. FRpicture RU @ OU Given UF @ UF reflexive prop. DFRU @ DFOU SSS ÐR @ ÐO CPCTC 58

Corresponding Parts of Congruent Triangles • Sometimes it is necessary to add an auxiliary line in order to complete a proof Statement Reason • For example, to prove ÐR @ ÐO in @ FO Given this. FRpicture RU @ OU Given UF @ UF Same segment DFRU @ DFOU SSS ÐR @ ÐO CPCTC 59