Triangles 4 3 Congruent Triangles Warm Up Lesson









































- Slides: 65

Triangles 4 -3 Congruent Triangles Warm Up Lesson Presentation Lesson Quiz Holt Geometry

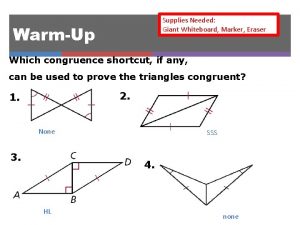
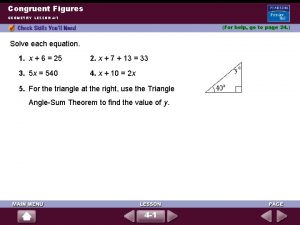
4 -3 Congruent Triangles Warm Up 1. Name all sides and angles of ∆FGH. FG, GH, FH, F, G, H 2. What is true about K and L? Why? ; Third s Thm. 3. What does it mean for two segments to be congruent? They have the same length. Holt Geometry

4 -3 Congruent Triangles Objectives Use properties of congruent triangles. Prove triangles congruent by using the definition of congruence. Holt Geometry

4 -3 Congruent Triangles November 8, 2013 Congruent Triangles What are the properties of congruent triangles using the definition of congruence? Holt Geometry

4 -3 Congruent Triangles Vocabulary corresponding angles corresponding sides congruent polygons Holt Geometry

4 -3 Congruent Triangles Geometric figures are congruent if they are the same size and shape. Corresponding angles and corresponding sides are in the same position in polygons with an equal number of sides. Two polygons are congruent polygons if and only if their corresponding sides are congruent. Thus triangles that are the same size and shape are congruent. Holt Geometry

4 -3 Congruent Triangles Holt Geometry

4 -3 Congruent Triangles Helpful Hint Two vertices that are the endpoints of a side are called consecutive vertices. For example, P and Q are consecutive vertices. Holt Geometry

4 -3 Congruent Triangles To name a polygon, write the vertices in consecutive order. For example, you can name polygon PQRS as QRSP or SRQP, but not as PRQS. In a congruence statement, the order of the vertices indicates the corresponding parts. Holt Geometry

4 -3 Congruent Triangles Helpful Hint When you write a statement such as ABC DEF, you are also stating which parts are congruent. Holt Geometry

4 -3 Congruent Triangles Example 1: Naming Congruent Corresponding Parts Given: ∆PQR ∆STW Identify all pairs of corresponding congruent parts. Angles: P S, Q T, R W Sides: PQ ST, QR TW, PR SW Holt Geometry

4 -3 Congruent Triangles Check It Out! Example 1 If polygon LMNP polygon EFGH, identify all pairs of corresponding congruent parts. Angles: L E, M F, N G, P H Sides: LM EF, MN FG, NP GH, LP EH Holt Geometry

4 -3 Congruent Triangles For example, you only need to know that two triangles have three pairs of congruent corresponding sides. This can be expressed as the following postulate. Holt Geometry

4 -3 Congruent Triangles Remember! Adjacent triangles share a side, so you can apply the Reflexive Property to get a pair of congruent parts. Holt Geometry

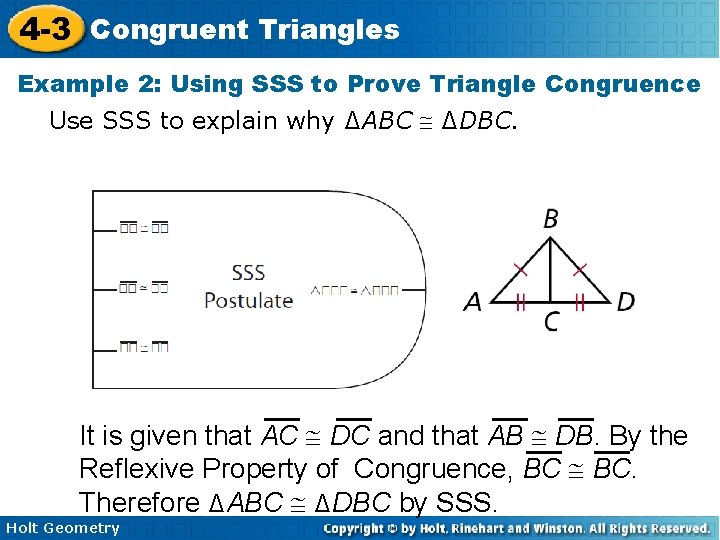
4 -3 Congruent Triangles Example 2: Using SSS to Prove Triangle Congruence Use SSS to explain why ∆ABC ∆DBC. It is given that AC DC and that AB DB. By the Reflexive Property of Congruence, BC BC. Therefore ∆ABC ∆DBC by SSS. Holt Geometry

4 -3 Congruent Triangles On your TABLE! Example 2 Use SSS to explain why ∆ABC ∆CDA. It is given that AB CD and BC DA. By the Reflexive Property of Congruence, AC CA. So ∆ABC ∆CDA by SSS. Holt Geometry

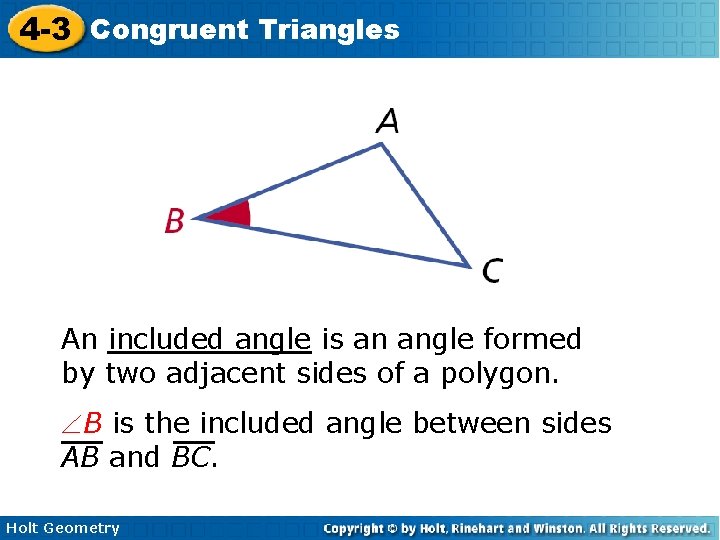
4 -3 Congruent Triangles An included angle is an angle formed by two adjacent sides of a polygon. B is the included angle between sides AB and BC. Holt Geometry

4 -3 Congruent Triangles It can also be shown that only two pairs of congruent corresponding sides are needed to prove the congruence of two triangles if the included angles are also congruent. Holt Geometry

4 -3 Congruent Triangles Holt Geometry

4 -3 Congruent Triangles Caution The letters SAS are written in that order because the congruent angles must be between pairs of congruent corresponding sides. Holt Geometry

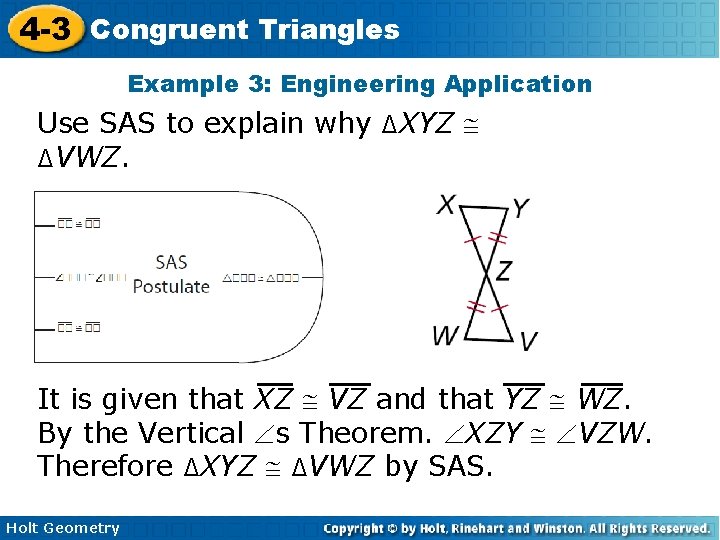
4 -3 Congruent Triangles Example 3: Engineering Application Use SAS to explain why ∆XYZ ∆VWZ. It is given that XZ VZ and that YZ WZ. By the Vertical s Theorem. XZY VZW. Therefore ∆XYZ ∆VWZ by SAS. Holt Geometry

4 -3 Congruent Triangles Check It Out! Example 3 Use SAS to explain why ∆ABC ∆DBC. It is given that BA BD and ABC DBC. By the Reflexive Property of , BC BC. So ∆ABC ∆DBC by SAS. Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Definitions Holt Geometry

4 -3 Congruent Triangles Definitions Holt Geometry

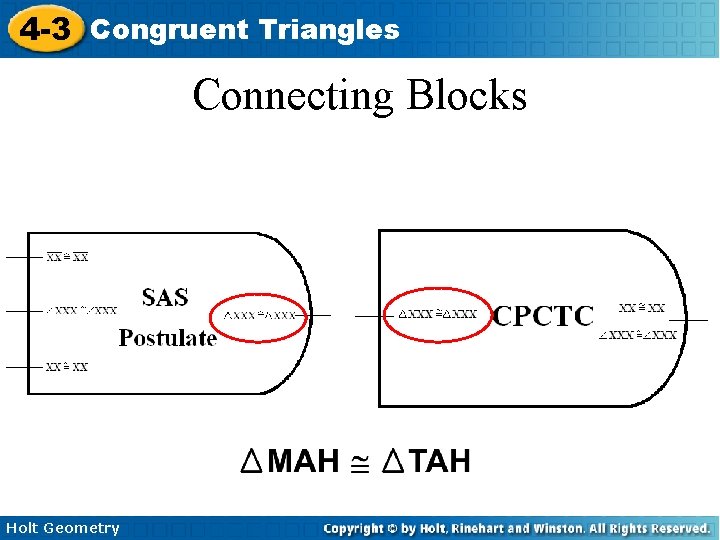
4 -3 Congruent Triangles Connecting Blocks Holt Geometry

4 -3 Congruent Triangles Connecting Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Definitions Holt Geometry

4 -3 Congruent Triangles Definitions Holt Geometry

4 -3 Congruent Triangles Connecting Blocks Holt Geometry

4 -3 Congruent Triangles Connecting Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Proof Blocks Holt Geometry

4 -3 Congruent Triangles Holt Geometry

4 -3 Congruent Triangles An included side is the common side of two consecutive angles in a polygon. The following postulate uses the idea of an included side. Holt Geometry

4 -3 Congruent Triangles Holt Geometry

4 -3 Congruent Triangles Example 4: Applying ASA Congruence Determine if you can use ASA to prove the triangles congruent. Explain. Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt Geometry

4 -3 Congruent Triangles Check It Out! Example 4 Determine if you can use ASA to prove NKL LMN. Explain. By the Alternate Interior Angles Theorem. KLN MNL. NL LN by the Reflexive Property. No other congruence relationships can be determined, so ASA cannot be applied. Holt Geometry

4 -3 Congruent Triangles You can use the Third Angles Theorem to prove another congruence relationship based on ASA. This theorem is Angle-Side (AAS). Holt Geometry

4 -3 Congruent Triangles Holt Geometry

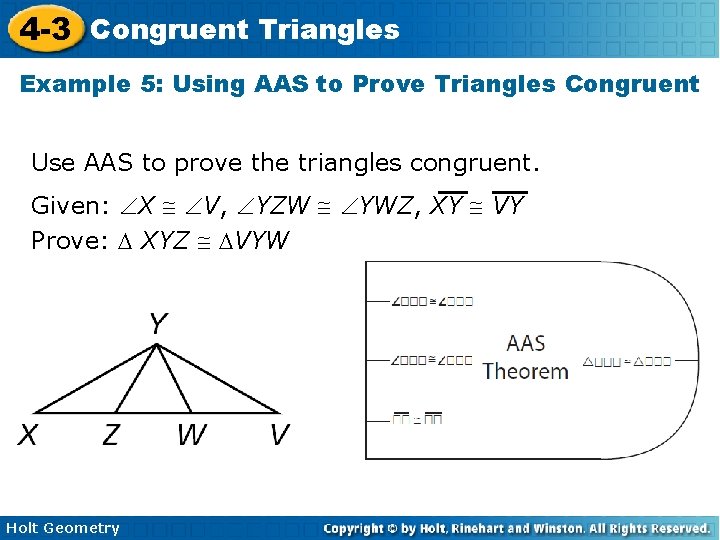
4 -3 Congruent Triangles Example 5: Using AAS to Prove Triangles Congruent Use AAS to prove the triangles congruent. Given: X V, YZW YWZ, XY VY Prove: XYZ VYW Holt Geometry

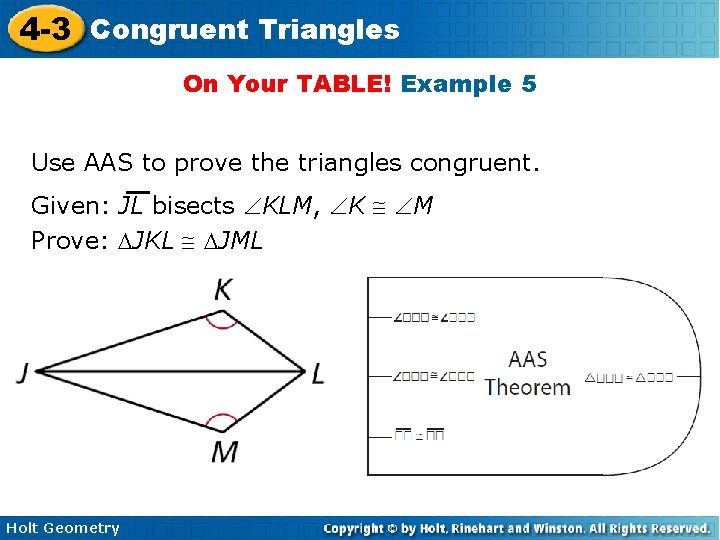
4 -3 Congruent Triangles On Your TABLE! Example 5 Use AAS to prove the triangles congruent. Given: JL bisects KLM, K M Prove: JKL JML Holt Geometry

4 -3 Congruent Triangles Holt Geometry

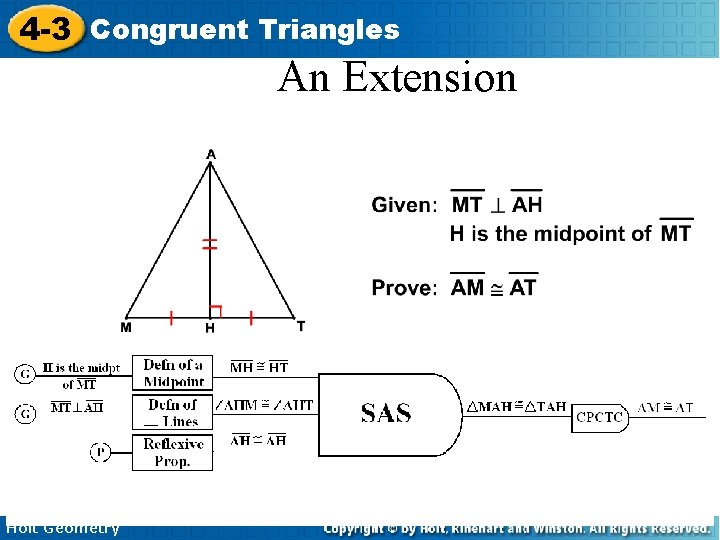
4 -3 Congruent Triangles An Extension Holt Geometry

4 -3 Congruent Triangles An Extension Holt Geometry

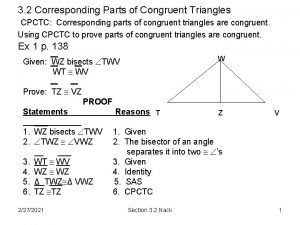
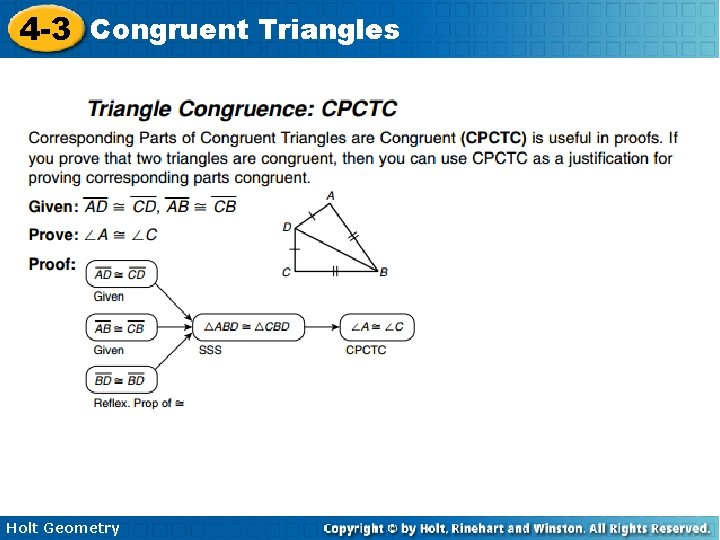
4 -3 Congruent Triangles An Extension Corresponding Parts of Congruent Triangles are Congruent Holt Geometry

4 -3 Congruent Triangles An Extension Corresponding parts of congruent triangles are congruent Holt Geometry

4 -3 Congruent Triangles An Extension Corresponding parts of congruent triangles are congruent Holt Geometry

4 -3 Congruent Triangles An Extension Corresponding parts of congruent triangles are congruent Holt Geometry

4 -3 Congruent Triangles On your TABLE Holt Geometry

4 -3 Congruent Triangles Connecting Blocks Holt Geometry

4 -3 Congruent Triangles An Extension Holt Geometry

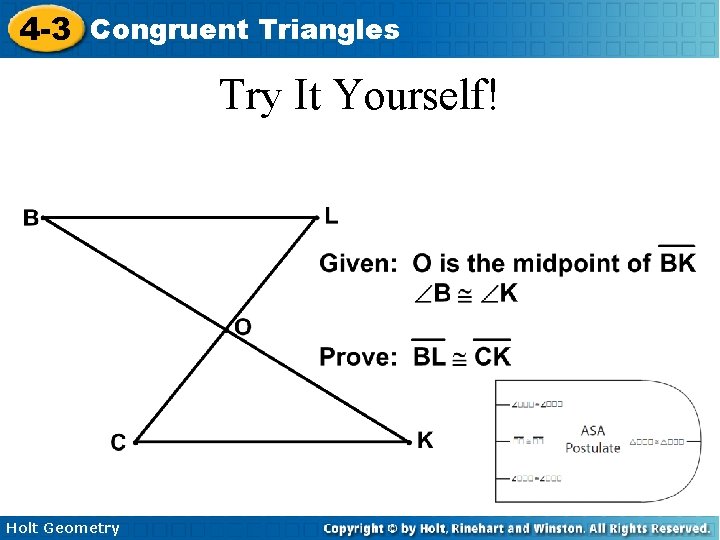
4 -3 Congruent Triangles Try It Yourself! Holt Geometry

4 -3 Congruent Triangles What are the properties of congruent triangles using the definition of congruence? The properties of congruent triangles are ………. The definition of congruence is………… Holt Geometry

4 -3 Congruent Triangles Summarize The Congruence postulates are…… CPCTC means……. When using ASA and SAS it is important to…. Something I found interesting was…. Holt Geometry In your PLANNER q Homework and Practice Workbook 4. 3, 4. 4, 4. 5 AND 4. 6 PG. 23, 24, 25, 26 q Review C-Notes (Questions, Circle, Underline, Clarify) q 11/12/2013 TEST: Unit 7
 Quiz 4-2 congruent triangles
Quiz 4-2 congruent triangles Isosceles and equilateral
Isosceles and equilateral Proving triangles congruent sss and sas
Proving triangles congruent sss and sas Quiz 4-2 congruent triangles sss and sas
Quiz 4-2 congruent triangles sss and sas Lesson 4-5 proving triangles congruent
Lesson 4-5 proving triangles congruent 4-5 triangle congruence asa aas and hl
4-5 triangle congruence asa aas and hl 4-4 proving triangles congruent
4-4 proving triangles congruent Classify each polygon
Classify each polygon Corresponding angles
Corresponding angles Flow proof geometry
Flow proof geometry Unit 4 homework 4 congruent triangles
Unit 4 homework 4 congruent triangles 4-4 congruent triangles
4-4 congruent triangles Similar and congruent triangles
Similar and congruent triangles Giant white board
Giant white board Congruent triangle shortcuts
Congruent triangle shortcuts Dr frost congruent triangles
Dr frost congruent triangles Congruent triangles worksheet
Congruent triangles worksheet Rhs congruence rule
Rhs congruence rule Chapter 4 congruent triangles
Chapter 4 congruent triangles Triangle congruence matching activity
Triangle congruence matching activity Asa
Asa How to prove triangles are congruent
How to prove triangles are congruent Trigonometry magic triangles
Trigonometry magic triangles Ways to prove triangles are congruent reference
Ways to prove triangles are congruent reference 4-4 proving triangles congruent
4-4 proving triangles congruent 4-3 congruent triangles
4-3 congruent triangles Triangles class 9 activity
Triangles class 9 activity Which triangles are congruent by asa?
Which triangles are congruent by asa? 4-4 proving triangles congruent asa aas
4-4 proving triangles congruent asa aas 4-4 using corresponding parts of congruent triangles
4-4 using corresponding parts of congruent triangles Quiz 4-1 congruent triangles
Quiz 4-1 congruent triangles 4-4 proving triangles congruent-sss sas answers
4-4 proving triangles congruent-sss sas answers 4-3 congruent triangles
4-3 congruent triangles 4-2 congruent triangles
4-2 congruent triangles 4-6 practice a triangle congruence cpctc answers
4-6 practice a triangle congruence cpctc answers 4-1 practice congruent figures
4-1 practice congruent figures 4-5 proving right triangles congruent
4-5 proving right triangles congruent Lesson 4-5 triangle congruence sss and sas
Lesson 4-5 triangle congruence sss and sas Using corresponding parts of congruent triangles
Using corresponding parts of congruent triangles Congruent triangles in architecture
Congruent triangles in architecture Which triangles are congruent
Which triangles are congruent What does congruent mean
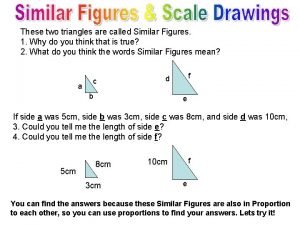
What does congruent mean Similar figures
Similar figures What is congruent
What is congruent 4-5 triangle congruence sss and sas
4-5 triangle congruence sss and sas Saa congruence postulate
Saa congruence postulate Name the congruent triangles
Name the congruent triangles Congruent triangles example
Congruent triangles example N is the midpoint of lw
N is the midpoint of lw Relfexive property
Relfexive property Similarity gcse
Similarity gcse Congruent triangles gcse questions
Congruent triangles gcse questions Chapter 4 congruent triangles
Chapter 4 congruent triangles Congruence postulates
Congruence postulates Lesson 4-1 congruent figures answers
Lesson 4-1 congruent figures answers Unit 3 lesson 4 proving angles congruent
Unit 3 lesson 4 proving angles congruent Lesson 1 congruent figures
Lesson 1 congruent figures Proving angles congruent
Proving angles congruent Unit 2 lesson 3 proving triangles similar
Unit 2 lesson 3 proving triangles similar Lesson 3 triangles answers
Lesson 3 triangles answers Classifying triangles lesson plan
Classifying triangles lesson plan 8-3 special right triangles
8-3 special right triangles Geometry 8-3 special right triangles
Geometry 8-3 special right triangles How to label hyp opp adj
How to label hyp opp adj Lesson 7-3
Lesson 7-3 Lesson 5 inequalities
Lesson 5 inequalities