Lesson 7 4 Right Triangle Trigonometry 1 In

Lesson 7 -4 Right Triangle Trigonometry 1

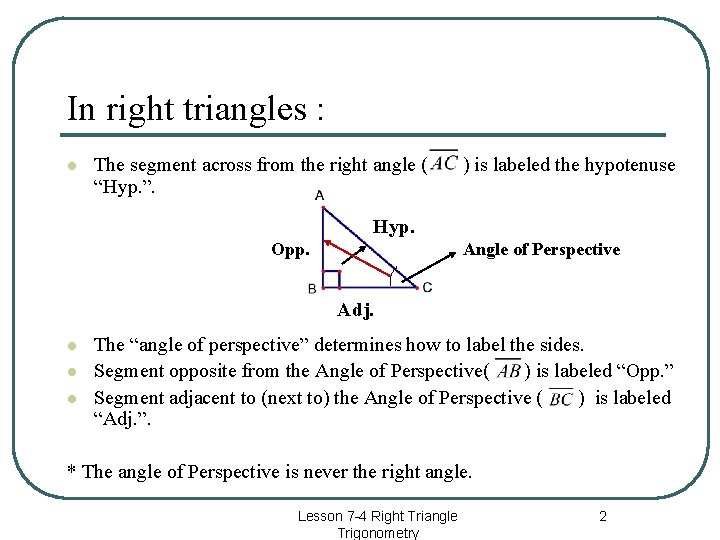
In right triangles : l The segment across from the right angle ( “Hyp. ”. ) is labeled the hypotenuse Hyp. Opp. Angle of Perspective Adj. l l l The “angle of perspective” determines how to label the sides. Segment opposite from the Angle of Perspective( ) is labeled “Opp. ” Segment adjacent to (next to) the Angle of Perspective ( ) is labeled “Adj. ”. * The angle of Perspective is never the right angle. Lesson 7 -4 Right Triangle Trigonometry 2

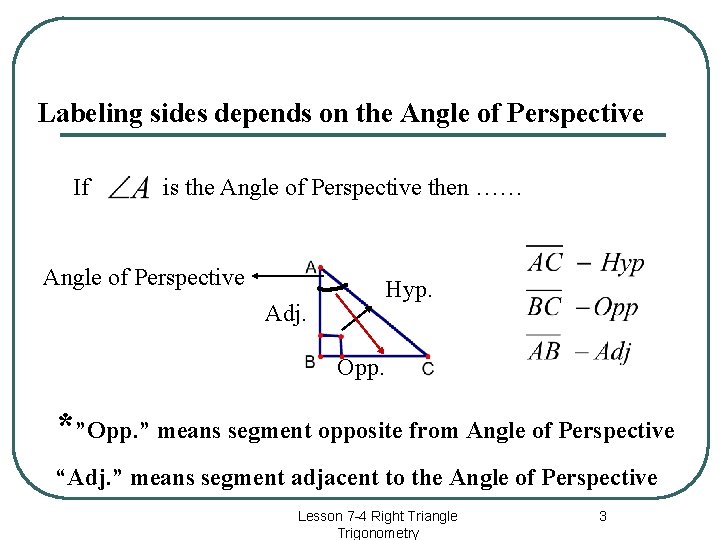
Labeling sides depends on the Angle of Perspective If is the Angle of Perspective then …… Angle of Perspective Hyp. Adj. Opp. *”Opp. ” means segment opposite from Angle of Perspective “Adj. ” means segment adjacent to the Angle of Perspective Lesson 7 -4 Right Triangle Trigonometry 3

If the Angle of Perspective is then Adj Hyp then Hyp Opp Adj Lesson 7 -4 Right Triangle Trigonometry 4

Trigonometry Ratios If Sin is the Angle of Perspective then …. . . = Hyp Opp Cos = tan = Adj Angle of Perspective Lesson 7 -4 Right Triangle Trigonometry 5

Example: Find the value of x. Step 1: Mark the “Angle of Perspective”. Step 2: Label the sides (Hyp / Opp / Adj). Step 3: Select a trigonometry ratio (sin/ cos / tan). Sin = Step 4: Substitute the values into the equation. Sin 25 = opp Hyp Angle of Perspective Adj Step 5: Solve the equation : Change Sin 25 into a decimal. Cross multiply and solve. = x = (0. 4226) (12) x = 5. 07 cm Lesson 7 -4 Right Triangle Trigonometry 6

Solving Trigonometric Equations There are only three possibilities for the placement of the variable ‘x”. Sin C = Sin xº = Sin 25 Sin xº = 0. 48 x = Sin (0. 48) x = 28. 6854 C = = 0. 4226 = x = (12) (0. 4226) x = 5. 04 cm Lesson 7 -4 Right Triangle Trigonometry Sin C = Sin 25 = 0. 4226 = x = 28. 4 cm 7

Remember “SOHCAHTOA” S – Sine is O – Opposite over H - Hypotenuse C – Cosine is A – Adjacent over H - Hypotenuse T – Tangent is O – Opposite over A - Adjacent Lesson 7 -4 Right Triangle Trigonometry 8