Proving Triangles are Congruent SSS and SAS Chapter

Proving Triangles are Congruent SSS and SAS Chapter 4. 4 Video 2: 21 -7: 42

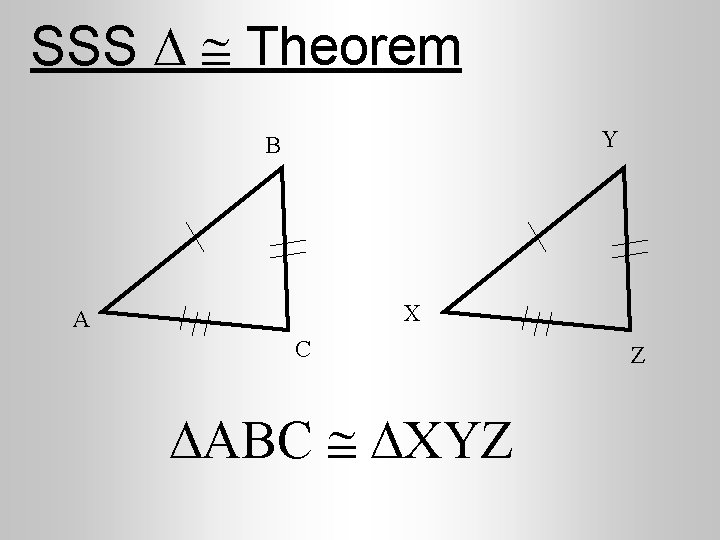
SSS Theorem • If all three sides of one triangle, are congruent to the corresponding sides in a second triangle, then the triangles are congruent.

SSS Theorem Y B X A C ABC XYZ Z

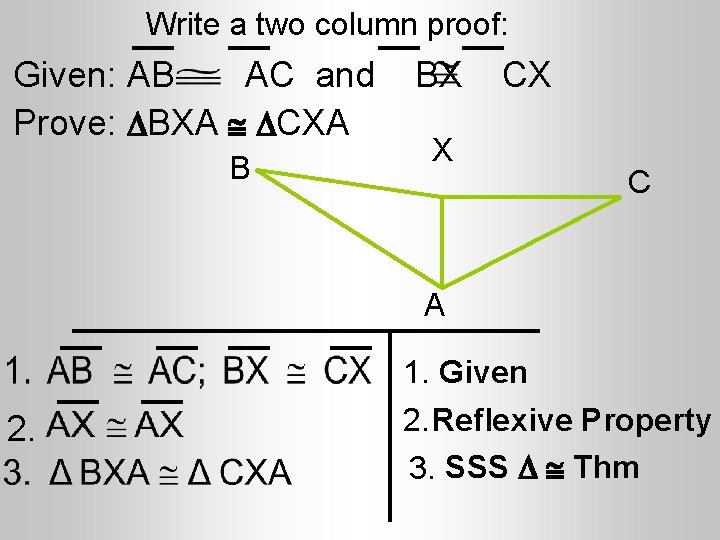
Write a two column proof: Given: AB AC and Prove: BXA CXA B BX X CX C A 2. 1. Given 2. Reflexive Property 3. SSS Thm

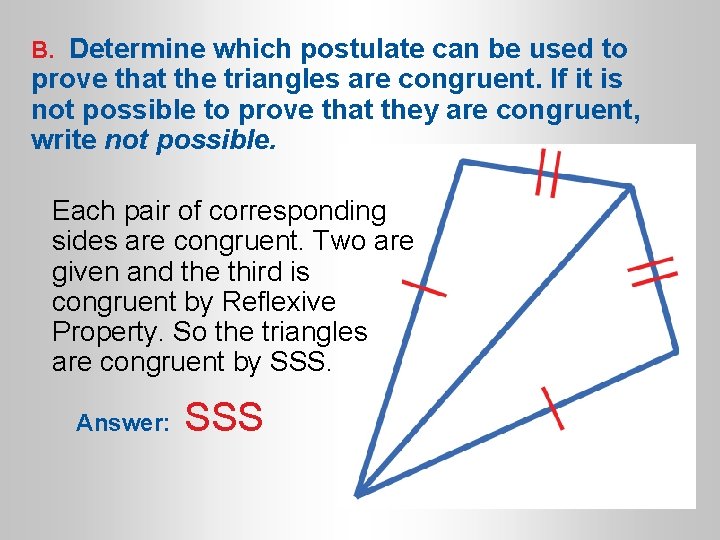
B. Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove that they are congruent, write not possible. Each pair of corresponding sides are congruent. Two are given and the third is congruent by Reflexive Property. So the triangles are congruent by SSS. Answer: SSS

Proof: Statements 1. 2. 3. ΔABG ΔCBG Reasons 1. Given reflexive 2. _____ 3. SSS

SAS Theorem • If two sides and the included angle of one triangle, are congruent to the corresponding sides and angle in a second triangle, then the triangles are congruent.

SAS Theorem Y B X A C ABC XYZ Z

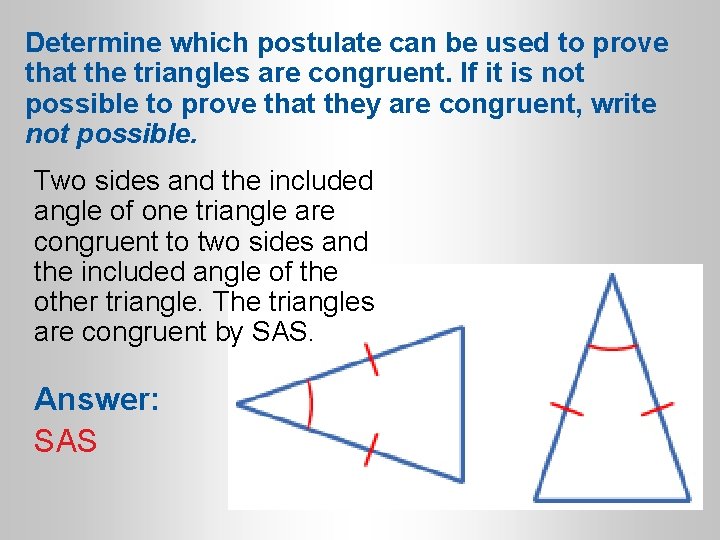
Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove that they are congruent, write not possible. Two sides and the included angle of one triangle are congruent to two sides and the included angle of the other triangle. The triangles are congruent by SAS. Answer: SAS

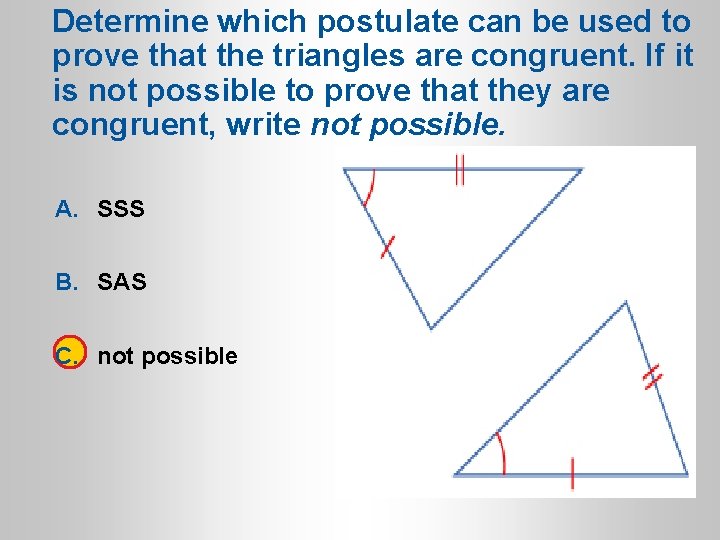
Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove that they are congruent, write not possible. A. SSS B. SAS C. not possible 1. 2. 3. A B C

Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove that they are congruent, write not possible. A. SSS B. SAS C. not possible 1. 2. 3. A B C

Homework Chapter 4 -4 • Pg 229 1 -6 all 9, 10 15 -18 all 31 33 -41 all