Thermodynamics and Equilibrium Thermodynamics Thermodynamics the study of

Thermodynamics and Equilibrium

Thermodynamics • Thermodynamics the study of the relationship between heat and other forms of energy in a chemical or physical process. • Describes systems whose states are determined by thermal parameters. – From Chapter 6: the change in enthalpy equals the heat of reaction at constant pressure – In this chapter we will define enthalpy in terms of the energy of the system. 2

First Law of Thermodynamics – The internal energy, U, is the sum of the kinetic and potential energies of the particles making up the system. U = Ek + Ep – Internal energy is a state function - a property of a system that depends only on its present state. 3
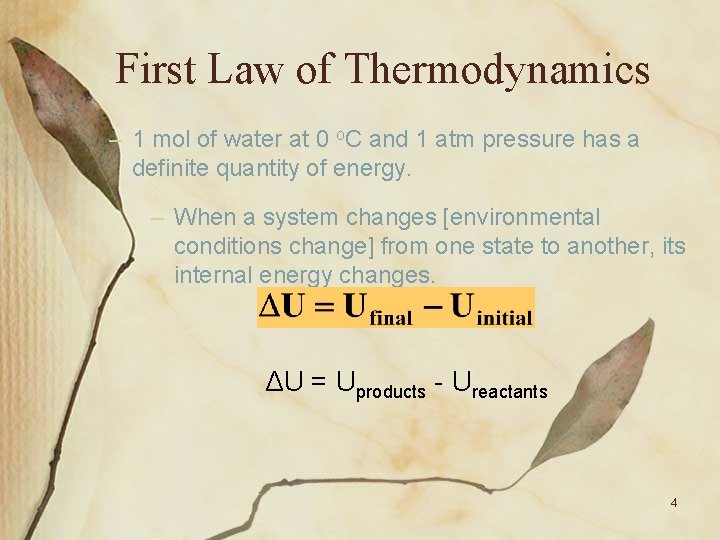
First Law of Thermodynamics – 1 mol of water at 0 o. C and 1 atm pressure has a definite quantity of energy. – When a system changes [environmental conditions change] from one state to another, its internal energy changes. ΔU = Uproducts - Ureactants 4

First Law of Thermodynamics – Changes in U manifest themselves as exchanges of energy between the system and surroundings. – These exchanges of energy are of two kinds; heat (q) and work (w). – ΔU = q + w 5

First Law of Thermodynamics – Heat is energy that moves into or out of a system because of a temperature difference between system and surroundings. – Work is the energy exchange that results when a force F moves an object through a distance d; work (w) = F d 6

First Law of Thermodynamics – Obeying our sign convention. Work done by the system is negative. Work done on the system is positive. Heat evolved by the system is negative. Heat absorbed by the system is positive. 7
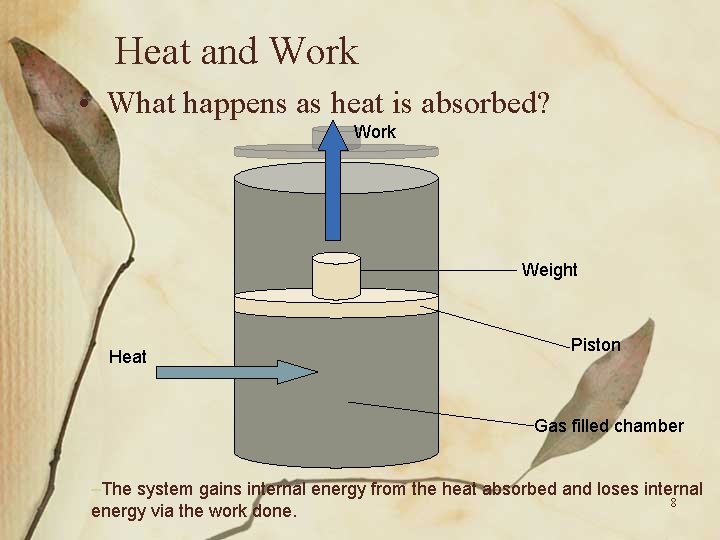
Heat and Work • What happens as heat is absorbed? Work Weight Heat Piston Gas filled chamber –The system gains internal energy from the heat absorbed and loses internal 8 energy via the work done.

First Law of Thermodynamics – The first law of thermodynamics states that the change in internal energy, U, equals heat plus work. 9

Heat of Reaction and Internal Energy • When a reaction is run in an open vessel (at constant P), any gases produced represent a potential source of “expansion” work. – When gases are produced, they exert force on the surroundings as pressure. – If the reaction is run at constant pressure, then the gases produced represent a change in volume analogous to a distance over which a force is exerted. 10

Heat of Reaction and Internal Energy – It follows therefore, that – (force x distance) – You can calculate the work done by a chemical reaction simply by multiplying the atmospheric pressure by the change in volume, V. 11

Heat of Reaction and Internal Energy – For example, when 1. 00 mol Zn reacts with excess HCl, 1. 00 mol H 2 is produced. qp = -152. 4 k. J – At 25 o. C and 1. 00 atm (1. 01 x 105 Pa), this amount of H 2 occupies 24. 5 L (24. 5 x 10 -3 m 3). – The work done by the chemical system in pushing back the atmosphere is 12

W = -PΔV • Therefore, since PV = n. RT – -PΔV = -Δn. RT – This indicates that work is done only if there is a change in the number of moles of gaseous reactants and products. 13

Heat of Reaction and Internal Energy – Relating the change in internal energy to the heat of reaction, you have 14

Heat of Reaction and Internal Energy – When the reaction occurs, the internal energy changes as the kinetic and potential energies change in going from reactants to products. – Energy leaves the system mostly as heat (qp = -152. 4 k. J) but partly as expansion work (-2. 47 k. J). 15

Determine if work is done, and its sign in the following rxn… Si. O 2(s) + 3 C(s) → Si. C(s) + 2 CO(g) Δn = # mol gaseous product - # moles gaseous reactants Δn = 2 – 0 Δn = 2 w= -PΔV=- Δn RT • The sign of work is the opposite of Δn – Work is done [b/c difference in gaseous moles] – Work is done by the system • b/c the sign of Δn is positive, so the sign of w is negative 16

• A 2. 00 g sample of hydrazine, N 2 H 4, is combusted in a bomb calorimeter containing 6400 g of water. The temperature increases 1. 17 o. C. The heat capacity of the calorimeter is 3. 76 k. J/o. C. • What is ΔU for hydrazine? N 2 H 4 + O 2 N 2 + 2 H 2 O ΔU = Uproducts – Ureactants – The energy changes in this situation are recorded in terms of heat and temperature. 17

• The heat causing the water temperature change… q. H 2 O = mΔTCp q. H 2 O = (6400 g)(1. 17 o. C)(4. 184 J/go. C) q. H 2 O = 31, 329 J q. H 2 O = 31. 329 k. J • Heat absorbed by calorimeter… 3. 76 k. J x 1. 17 o. C = 4. 39 k. J o. C • Total heat = 31. 329 k. J + 4. 39 k. J = 35. 72 k. J • ΔU = -35. 72 k. J/ 2 g. N 2 H 4 • Exothermic rxn 18

Enthalpy and Enthalpy Change • In Chapter 6, we tentatively defined enthalpy in terms of the relationship of H to the heat at constant pressure. – We now define enthalpy, H , precisely as the quantity U + PV. H = U + PV – allows pressure to be variable – H is a state function. 19
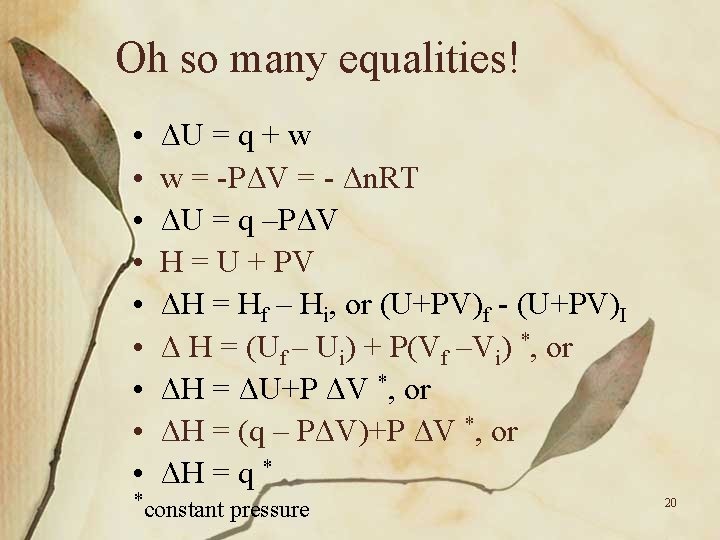
Oh so many equalities! • • • ΔU = q + w w = -PΔV = - Δn. RT ΔU = q –PΔV H = U + PV ΔH = Hf – Hi, or (U+PV)f - (U+PV)I Δ H = (Uf – Ui) + P(Vf –Vi) *, or ΔH = ΔU+P ΔV *, or ΔH = (q – PΔV)+P ΔV *, or ΔH = q * *constant pressure 20

Enthalpy and Enthalpy Change • In Chapter 6, we tentatively defined enthalpy in terms of the relationship of H to the heat at constant pressure. – This means that at a given temperature and pressure, a given amount of a substance has a definite enthalpy. – Therefore, if you know the enthalpies of substances, you can calculate the change in enthalpy, H , for a reaction. 21
Enthalpy and Enthalpy Change – In practice, we measure certain heats of reactions and use them to tabulate enthalpies of formation, Hof. – Standard enthalpies of formation for selected compounds are listed in Table 6. 2 and in Appendix C. 22

Enthalpy and Enthalpy Change – The standard enthalpy change for a reaction is 23

Spontaneous Processes and Entropy • A spontaneous process is a physical or chemical change that occurs by itself. – Examples include: A rock at the top of a hill rolls down. Heat flows from a hot object to a cold one. An iron object rusts in moist air. – These processes occur without requiring an outside force and continue until equilibrium is reached. (see Figure 19. 4) 24

Entropy and the Second Law of Thermodynamics – Entropy, S , is a thermodynamic quantity that is a measure of the randomness or disorder of a system. – The SI unit of entropy is joules per Kelvin (J/K) and, like enthalpy, is a state function. 25

Entropy and the Second Law of Thermodynamics • The second law of thermodynamics states that the total entropy of a system and its surroundings always increases for a spontaneous process. – The net change in entropy of the system, S , equals the sum of the entropy created during the spontaneous process and the change in energy associated with the heat flow. 26

Entropy and the Second Law of Thermodynamics – In other words, (For a spontaneous process) 27

Entropy and the Second Law of Thermodynamics – Normally, the quantity of entropy created during a spontaneous process cannot be directly measured. – If we delete it from our equation, we can conclude (For a spontaneous process) 28

Entropy and the Second Law of Thermodynamics – The restatement of the second law is as follows: – For a spontaneous process, the change in entropy of the system is greater than the heat divided by the absolute temperature. – Under these conditions, no significant amount of entropy is created. – The entropy results entirely from the absorption of heat. Therefore, (For an equilibrium process) 29

Entropy Change for a Phase Transition • If during a phase transition, such as ice melting, heat is slowly absorbed by the system, it remains near equilibrium as the ice melts. – Other phase changes, such as vaporization of a liquid, also occur under equilibrium conditions. – Therefore, you can use the equation to obtain the entropy change for a phase change. 30

A Problem To Consider • The heat of vaporization, Hvap of carbon tetrachloride, CCl 4, at 25 o. C is 43. 0 k. J/mol. If 1 mol of liquid CCl 4 has an entropy of 214 J/K, what is the entropy of 1 mol of the vapor at this temperature? – When liquid CCl 4 evaporates, it absorbs heat: Hvap = 43. 0 k. J/mol (43. 0 x 103 J/mol) at 25 o. C, or 298 K. The entropy change, S, is – Remember H = q 31

A Problem To Consider • The heat of vaporization, Hvap of carbon tetrachloride, CCl 4, at 25 o. C is 43. 0 k. J/mol. If 1 mol of liquid CCl 4 has an entropy of 214 J/K, what is the entropy of 1 mol of the vapor at this temperature? – In other words, 1 mol of CCl 4 increases in entropy by 144 J/K when it vaporizes. – The entropy of 1 mol of vapor equals the entropy of 1 mol of liquid (214 J/K) plus 144 J/K. 32

Entropy, Enthalpy, and Spontaneity • Now you can see how thermodynamics is applied to the question of reaction spontaneity. – Recall that the heat at constant pressure, qp , equals the enthalpy change, H. = qp – The second law for a spontaneous reaction at constant temperature and pressure becomes (Spontaneous reaction, constant T and P) 33

Entropy, Enthalpy, and Spontaneity – Rearranging this equation, we find (Spontaneous reaction, constant T and P) – Thus for a reaction to be spontaneous, H-T S must be negative. – If H-TDS is positive, the reverse reaction is spontaneous. – If H-T S=0, the reaction is at equilibrium 34

Entropy, Enthalpy, and Spontaneity • Spontaneity is favored by: – Release of energy • Exothermicity – Increasing disorder in a system • Ex: dissolving, evaporating 35

Standard Entropies and the Third Law of Thermodynamics • The third law of thermodynamics states that a substance that is perfectly crystalline at 0 K has an entropy of zero. ΔS = 0 for crystal – When temperature is raised, however, the substance becomes more disordered as it absorbs heat. – The entropy of a substance is determined by measuring how much heat is required to change its temperature per Kelvin degree. 36

Standard Entropies and the Third Law of Thermodynamics • The standard entropy of a substance or ion , also called its absolute entropy, So, is the entropy value for the standard state of the species. – Standard state implies: – 25 o. C – 1 atm pressure – 1 M for dissolved substances. 37

Standard Entropies and the Third Law of Thermodynamics • The standard entropy of a substance or ion , also called its absolute entropy, So, is the entropy value for the standard state of the species. – Note that the elements have nonzero values, unlike standard enthalpies of formation, Hfo , which by convention, are zero. 38

Standard Entropies and the Third Law of Thermodynamics • The standard entropy of a substance or ion , also called its absolute entropy, So, is the entropy value for the standard state of the species. – The symbol So, rather than So, is used for standard entropies to emphasize that they originate from the third law. 39

Entropy Change for a Reaction • You can calculate the entropy change for a reaction using a summation law, similar to the way you obtained Ho. – Even without knowing the values for the entropies of substances, you can sometimes predict the sign of So for a reaction. 40

Entropy Change for a Reaction – The entropy usually increases in the following situations: 1. A reaction in which a molecule is broken into two or more smaller molecules. 2. A reaction in which there is an increase in the moles of gases. 3. A process in which a solid changes to liquid or gas or a liquid changes to gas. 41

A Problem To Consider • Calculate the change in entropy, So, at 25 o. C for the reaction in which urea is formed from NH 3 and CO 2. The standard entropy of NH 2 CONH 2 is 174 J/(mol. K). – The calculation is similar to that used to obtain Ho from standard enthalpies of formation. 42

A Problem To Consider • Calculate the change in entropy, So, at 25 o. C for the reaction in which urea is formed from NH 3 and CO 2. The standard entropy of NH 2 CONH 2 is 174 J/(mol. K). So: 2 x 193 214 174 70 43

Enthalpy v. Entropy for spontaneous reactions • Enthalpy Ho – Measures relative to standard state – Can be + or – ΔHo = Σn. Hoprod – Σn. Horeact – k. J / mol rxn – Deals w/ entire reaction • Entropy So – Measures relative to absolute zero – Always + ΔSo = Σn. Soprod – Σn. Soreact – J / mol K – Deals w. a substance 44

Free Energy Concept • The American physicist J. Willard Gibbs introduced the concept of free energy (sometimes called the Gibbs free energy), G, which is a thermodynamic quantity defined by the equation – State function G=H-TS. – Calculates the maximum energy available in the form of work. – Gives a direct criterion for spontaneity of reaction. 45

Free Energy and Spontaneity • Changes in H and S during a reaction result in a change in free energy, G , given by the equation – Thus, if you can show that if G is negative at a given temperature and pressure, you can predict that the reaction will be spontaneous. 46

Standard Free-Energy Change • The standard free energy change, Go, is the free energy change that occurs when reactants and products are in their standard states. 47

A Problem To Consider • What Wh is the standard free energy change, Go, for the following reaction at 25 o. C? Use values of Hfo and So, from reference tables. Hfo: 0 So: 191. 5 0 3 x 130. 6 2 x (-45. 9) k. J 2 x 193 J/K – Place below each formula the values of Hfo and So multiplied by stoichiometric coefficients. 48

A Problem To Consider • What is the standard free energy change, Go, for the following reaction at 25 o. C? Use values of Hfo and So, from reference tables. – You can calculate Ho and So using their respective summation laws. 49

A Problem To Consider • What is the standard free energy change, Go, for the following reaction at 25 o. C? Use values of Hfo and So, from reference tables. – You can calculate Ho and So using their respective summation laws. 50

A Problem To Consider • What is the standard free energy change, Go, for the following reaction at 25 o. C? Use values of Hfo and So, from Tables 6. 2 and 19. 1. – Now substitute into our equation for Go. Note that So is converted to k. J/K. 51

Standard Free Energies of Formation • The standard free energy of formation, Gfo, of a substance is the free energy change that occurs when 1 mol of a substance is formed from its elements in their most stable states at 1 atm pressure and 25 o. C. – By tabulating Gfo for substances you can calculate the Go for a reaction by using a summation law. 52

A Problem To Consider • Calculate Go for the combustion of 1 mol of ethanol, C 2 H 5 OH, at 25 o. C. Use the standard free energies of formation. Gfo: -174. 8 0 2(-394. 4) 3(-228. 6)k. J – Place below each formula the values of Gfo multiplied by stoichiometric coefficients. 53

A Problem To Consider • Calculate Go for the combustion of 1 mol of ethanol, C 2 H 5 OH, at 25 o. C. Use the standard free energies of formation given in Table 19. 2. Gfo: -174. 8 0 2(-394. 4) 3(-228. 6)k. J – You can calculate Go using the summation law. 54

A Problem To Consider • Calculate Go for the combustion of 1 mol of ethanol, C 2 H 5 OH, at 25 o. C. Use the standard free energies of formation given in Table 19. 2. Gfo: -174. 8 0 2(-394. 4) 3(-228. 6)k. J – You can calculate Go using the summation law. 55

o G as a Criteria for Spontaneity • The following rules are useful in judging the spontaneity of a reaction. 1. When Go is a large negative number (more negative than about – 10 k. J), the reaction is spontaneous as written, and the reactants transform almost entirely to products when equilibrium is reached. 56

o G as a Criteria for Spontaneity • The following rules are useful in judging the spontaneity of a reaction. 2. When Go is a large positive number (more positive than about +10 k. J), the reaction is nonspontaneous as written, and reactants do not give significant amounts of product at equilibrium. 57

o G as a Criteria for Spontaneity • The following rules are useful in judging the spontaneity of a reaction. 3. When Go is a small negative or positive value (less than about 10 k. J), the reaction gives an equilibrium mixture with significant amounts of both reactants and products. 58

o G as a Criteria for Spontaneity In Summary: • ΔGo < (–)10 k. J – spontaneous • ΔGo > (+)10 k. J – nonspontaneous • (-)10 k. J <ΔGo > (+)10 k. J – equilibrium – @ equilibrium ΔGo is usually set equal to zero. – ΔGo = 0 – This assumption is useful for many calculations. 59

ΔGo at equilibrium At what temperature does the reaction Sn. O 2+2 CO 2+Sn reach equilibrium? Given: ΔHo=14. 7 k. J/mol; ΔSo=31. 21 J/mol K ΔG=ΔH-TΔS 0=ΔH-TΔS ΔH = T ΔS 60

ΔGo at equilibrium ΔH = T ΔS 14. 7 k. J/mol = T. 03121 k. J/mol K 470. 7 K = T 197. 7 o. C 61

Maximum Work • Often reactions are not carried out in a way that does useful work. – As a spontaneous reaction occurs, the free energy of the system decreases and entropy is produced, but no useful work is obtained. – Remember that in any spontaneous rxn. S increases, so the quantity subtracted from H increases. 62

Maximum Work – In principle, if a reaction is carried out to obtain the maximum useful work, no entropy is produced. ( S = 0) – G = H, when S = 0 63

Maximum Work • Often reactions are not carried out in a way that does useful work. – It can be shown that the maximum useful work, wmax , for a spontaneous reaction is G. – The term free energy comes from this result. 64

Free Energy Change During Reaction • As a system approaches equilibrium, the instantaneous change in free energy approaches zero. – As the reaction proceeds, the free energy eventually reaches its minimum value. – At that point, G = 0, and the net reaction stops; it comes to equilibrium. 65
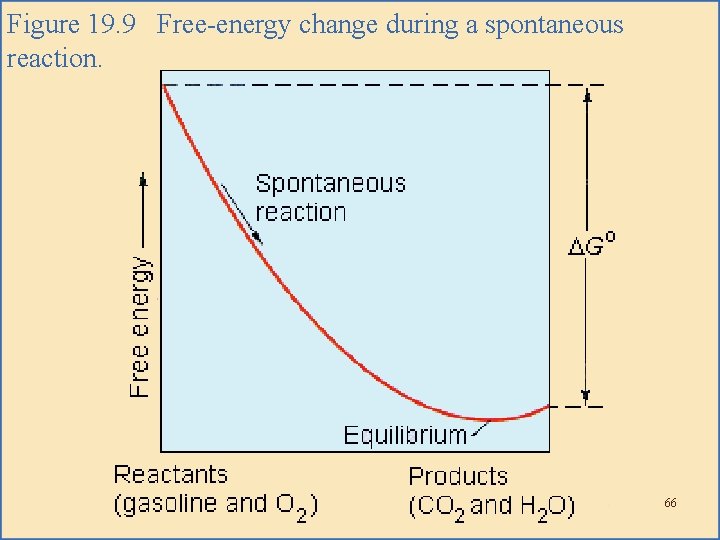
Figure 19. 9 Free-energy change during a spontaneous reaction. 66

Free Energy Change During Reaction • As a system approaches equilibrium, the instantaneous change in free energy approaches zero. – During a nonspontaneous reaction – there is a small decrease in free energy as the system goes to equilibrium. 67
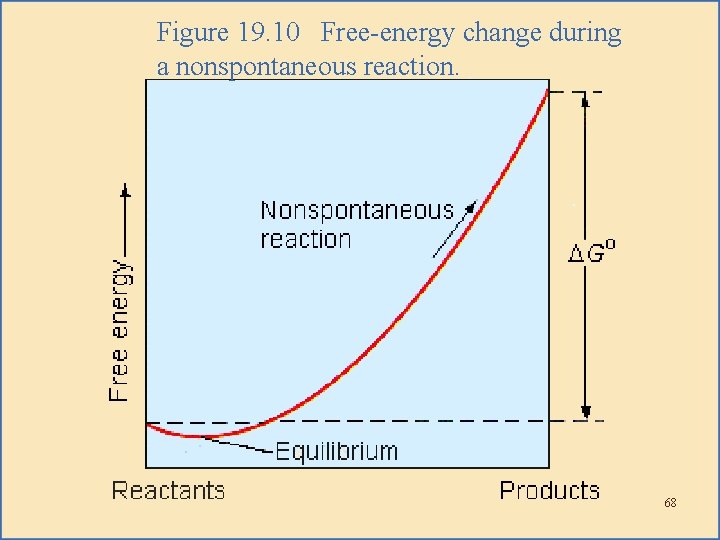
Figure 19. 10 Free-energy change during a nonspontaneous reaction. 68

Relating Constant o G to the Equilibrium • The free energy change when reactants are in non-standard states (other than 1 atm pressure or 1 M) is related to the standard free energy change, Go, by the following equation. – Here Q is thermodynamic form of the reaction quotient. 69

Relating Go to the Equilibrium Constant • The free energy change when reactants are in non-standard states (other than 1 atm pressure or 1 M) is related to the standard free energy change, Go, by the following equation. – G represents an instantaneous change in free energy at some point in the reaction approaching equilibrium. 70

Relating Go to the Equilibrium Constant • The free energy change when reactants are in non-standard states (other than 1 atm pressure or 1 M) is related to the standard free energy change, Go, by the following equation. – At equilibrium, G=0 and the reaction quotient Q becomes the equilibrium constant K. 71

Relating Go to the Equilibrium Constant • The free energy change when reactants are in non-standard states (other than 1 atm pressure or 1 M) is related to the standard free energy change, Go, by the following equation. – At equilibrium, G=0 and the reaction quotient Q becomes the equilibrium constant K. 72

Relating Go to the Equilibrium Constant • This result easily rearranges to give the basic equation relating the standard freeenergy change to the equilibrium constant. – When K > 1 , the ln K is positive and Go is negative. – When K < 1 , the ln K is negative and Go is positive. 73

A Problem To Consider • Find the value for the equilibrium constant, K, at 25 o. C (298 K) for the following reaction. The standard free-energy change, Go, at 25 o. C equals – 13. 6 k. J. – Rearrange the equation Go=-RTln. K to give 74

A Problem To Consider • Find the value for the equilibrium constant, K, at 25 o. C (298 K) for the following reaction. The standard free-energy change, Go, at 25 o. C equals – 13. 6 k. J. – Substituting numerical values into the equation, 75

A Problem To Consider • Find the value for the equilibrium constant, K, at 25 o. C (298 K) for the following reaction. The standard free-energy change, Go, at 25 o. C equals – 13. 6 k. J. – Hence, 76

Spontaneity and Temperature Change • All of the four possible choices of signs for Ho and So give different temperature behaviors for Go. Ho – + – So + – – Go – + + or – + + + or – Description Spontaneous at all T Nonspontaneous at all T Spontaneous at low T; Nonspontaneous at high T Nonspontaneous at low T; Spontaneous at high T 77

Calculation of Go at Various Temperatures • In this method you assume that Ho and So are essentially constant with respect to temperature. – You get the value of GTo at any temperature T by substituting values of Ho and So at 25 o. C into the following equation. 78

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K 79

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K 80

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – Now you substitute Ho, So (=0. 1590 k. J/K), and T (=298 K) into the equation for Gfo. 81

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K So the reaction is nonspontaneous at 25 o. C. 82

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – Now we’ll use 1000 o. C (1273 K) along with our previous values for Ho and So. 83

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – Now we’ll use 1000 o. C (1273 K) along with our previous values for Ho and So. So the reaction is spontaneous at 1000 o. C. 84

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – To determine the minimal temperature for spontaneity, we can set Gfº=0 and solve for T. 85

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – To determine the minimal temperature for spontaneity, we can set Gfº=0 and solve for T. 86

A Problem To Consider • Find the Go for the following reaction at 25 o. C and 1000 o. C. Relate this to reaction spontaneity. Hfo: -1206. 9 So: 92. 9 -635. 1 38. 2 -393. 5 k. J 213. 7 J/K – Thus, Ca. CO 3 should be thermally stable until its heated to approximately 848 o. C. 87

Bond Energy (BE) • Energy required to break one mole of covalent bonds and form products. – All substances are in the gaseous state at constant temperature and pressure – Bond Energy = Bond Enthalpy – ΔHorxn= ΣBEreactants-ΣBEproducts, or – ΔHorxn= ΣBEbroken-ΣBEformed 88

Estimate the enthalpy for the combustion of 1 mole of butane (C 4 H 10). • C 4 H 10 + 13/2 O 2 4 CO 2 + 5 H 2 O • Write the structural formula. H H H C C H + 13/2 O=O 4 O=C=O + 5 H-O-H H H 3 C-C and 10 C-H 13/2 O=O 8 C=O 10 H-O ΔH =[3(347) +10(414) +13/2(498)]-[8(741) + 10(464)] =[1041 + 4140+3237]-[5928 -4640] =8418 – 10, 568 =-2150 k. J/mol 89

Operational Skills • • Calculating the entropy change for a phase transition Predicting the sign of the entropy change of a reaction Calculating So for a reaction Calculating Go from Ho and So Calculating Go from standard free energies of formation Interpreting the sign of Go Writing the expression for a thermodynamic equilibrium constant • Calculating K from the standard free energy change • Calculating Go and K at various temperatures 90

Animation: Work Versus Energy Flow (Click here to open Quick. Time animation) Return to slide 6 91

Animation: Spontaneous Reaction (Click here to open Quick. Time animation) Return to slide 21 92
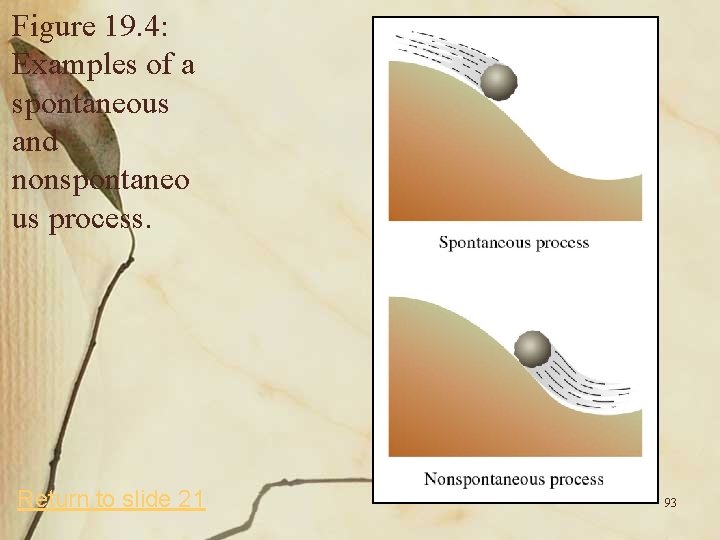
Figure 19. 4: Examples of a spontaneous and nonspontaneo us process. Return to slide 21 93
- Slides: 93