The Laplacian Matrices of Graphs Daniel A Spielman






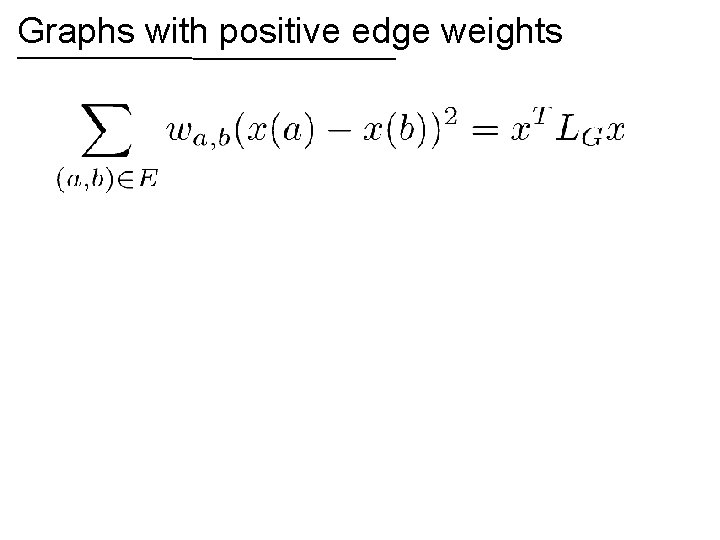





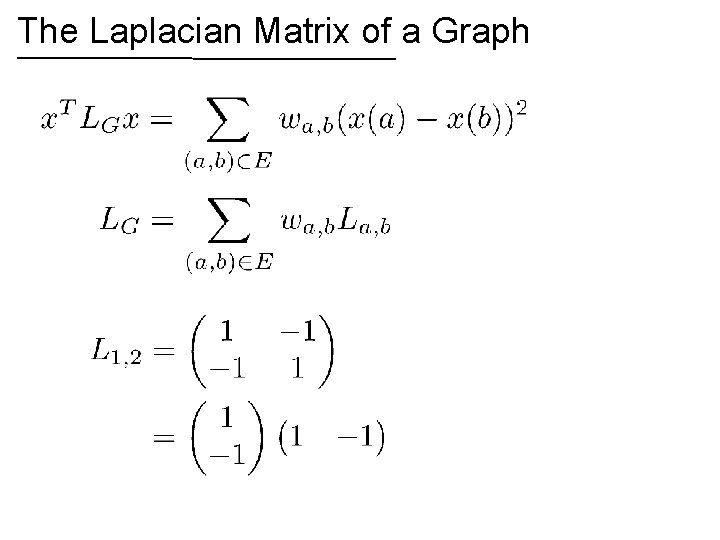






























- Slides: 81

The Laplacian Matrices of Graphs Daniel A. Spielman ISIT, July 12, 2016

Outline Laplacians Interpolation on graphs Resistor networks Spring networks Graph drawing Clustering Linear programming Sparsification Solving Laplacian Equations Best results The simplest algorithm

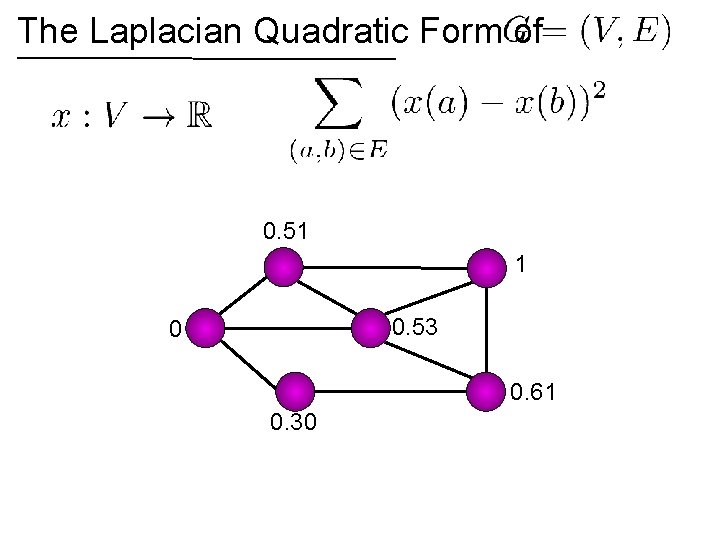
Interpolation on Graphs (Zhu, Ghahramani, Lafferty ’ 0 Interpolate values of a function at all vertices from given values at a few vertices. Minimize Subject to given values CDC 20 0 CDC 27 ANAPC 10 ANAPC 2 ANAPC 5 UBE 2 C 1

Interpolation on Graphs (Zhu, Ghahramani, Lafferty ’ 0 Interpolate values of a function at all vertices from given values at a few vertices. Minimize Subject to given values 0. 51 0 CDC 27 0. 30 ANAPC 10 ANAPC 2 ANAPC 5 1 0. 53 UBE 2 C 0. 61

Interpolation on Graphs (Zhu, Ghahramani, Lafferty ’ 0 Interpolate values of a function at all vertices from given values at a few vertices. Minimize Subject to given values 0. 51 0 CDC 27 0. 30 ANAPC 10 ANAPC 2 ANAPC 5 1 0. 53 UBE 2 C 0. 61

Interpolation on Graphs (Zhu, Ghahramani, Lafferty ’ 0 Interpolate values of a function at all vertices from given values at a few vertices. Minimize Subject to given values 0. 51 0 CDC 27 0. 30 ANAPC 10 ANAPC 2 ANAPC 5 1 0. 53 UBE 2 C 0. 61 Take derivatives. Minimize by solving Laplacian

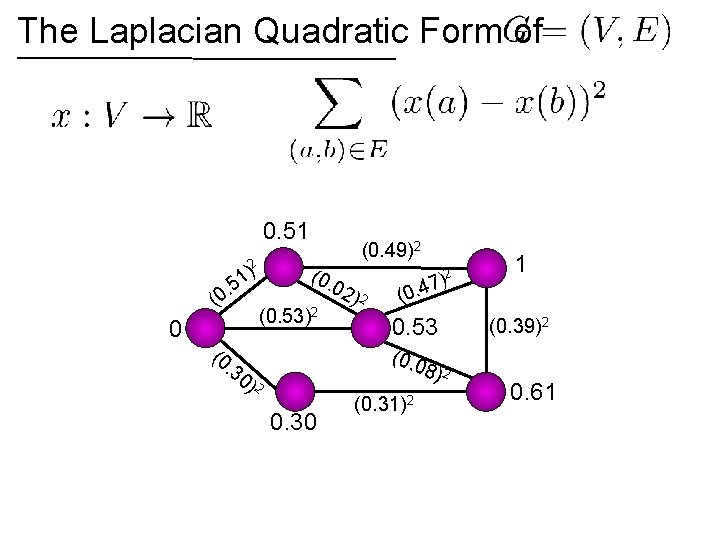
The Laplacian Quadratic Form of 0. 51 1 0. 53 0 0. 61 0. 30

The Laplacian Quadratic Form of 0. 51 2 ) 1 (0. 5 . (0 0 (0 (0. 49)2 02 (0. 53)2 )2 2 ) 7 4 (0. 0. 53 (0. 0 . 3 0) 2 0. 30 1 (0. 31)2 8) 2 (0. 39)2 0. 61
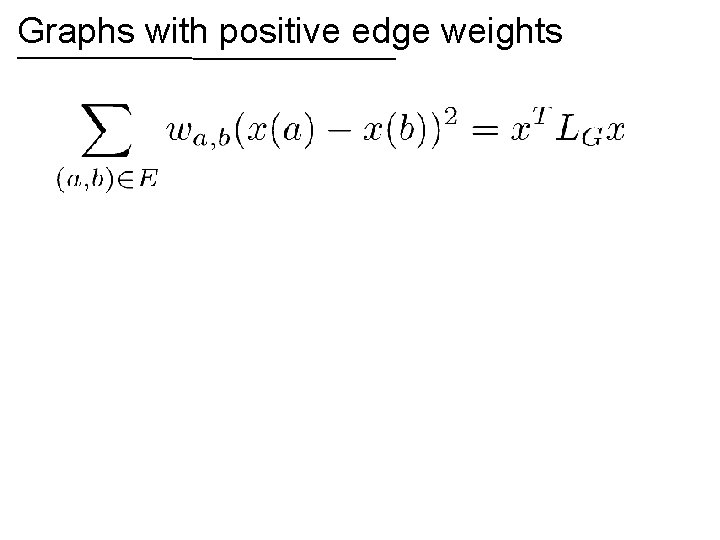
Graphs with positive edge weights

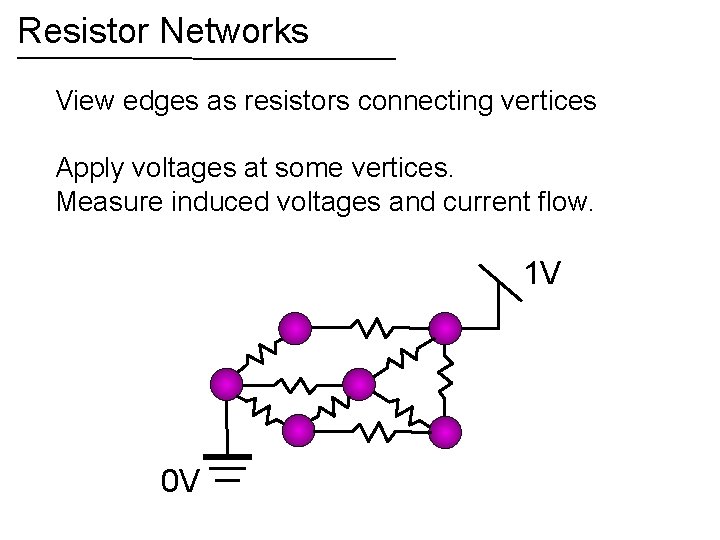
Resistor Networks View edges as resistors connecting vertices Apply voltages at some vertices. Measure induced voltages and current flow. 1 V 0 V

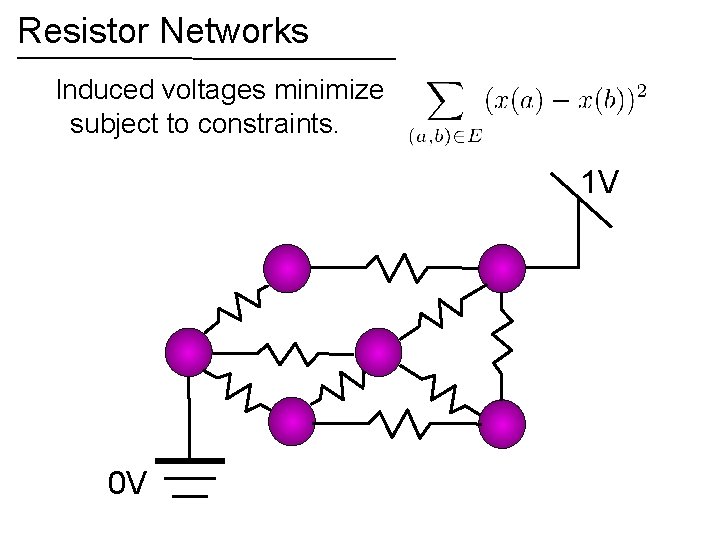
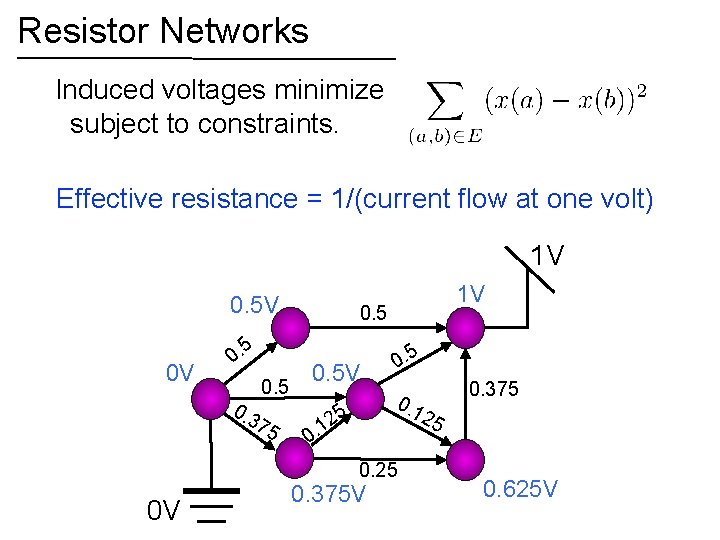
Resistor Networks Induced voltages minimize subject to constraints. 1 V 0 V

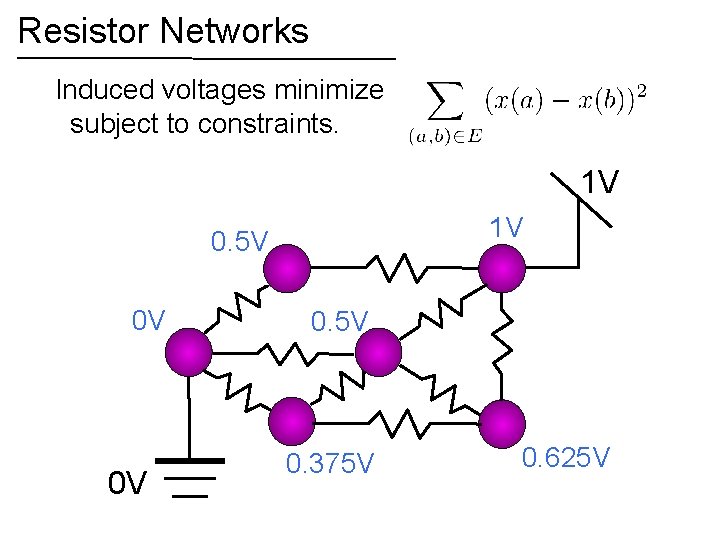
Resistor Networks Induced voltages minimize subject to constraints. 1 V 1 V 0. 5 V 0 V 0 V 0. 5 V 0. 375 V 0. 625 V

Resistor Networks Induced voltages minimize subject to constraints. 1 V 1 V 0. 5 V 0 V 0 V 0. 5 V 0. 375 V 0. 625 V

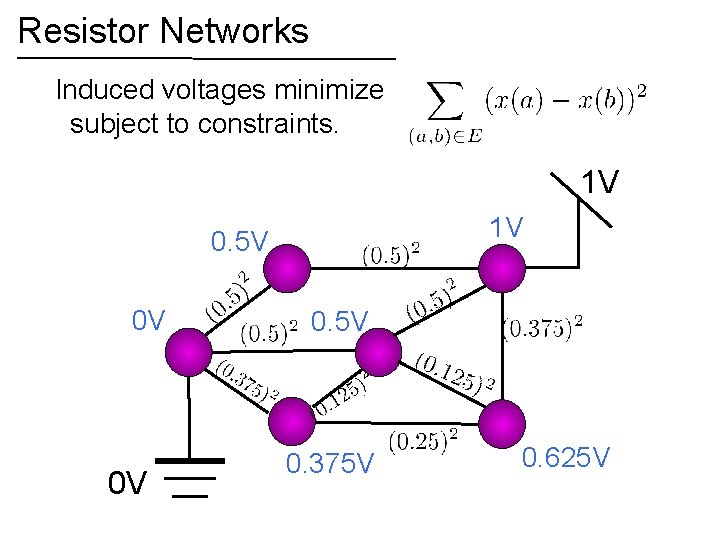
Resistor Networks Induced voltages minimize subject to constraints. Effective resistance = 1/(current flow at one volt) 1 V 0. 5 5 0 V 0. 3 0. 5 75 1 V 0. 5 0. 1 2 25 5 1 0. 25 0 V 0. 375 V 0. 625 V

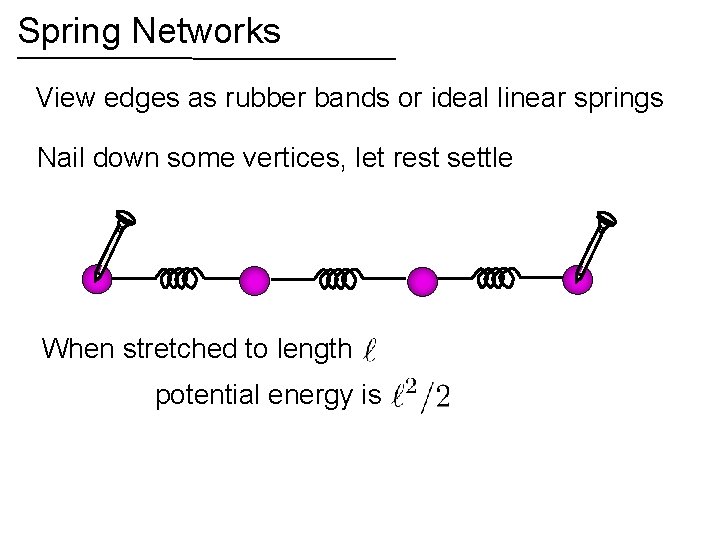
Spring Networks View edges as rubber bands or ideal linear springs Nail down some vertices, let rest settle When stretched to length potential energy is

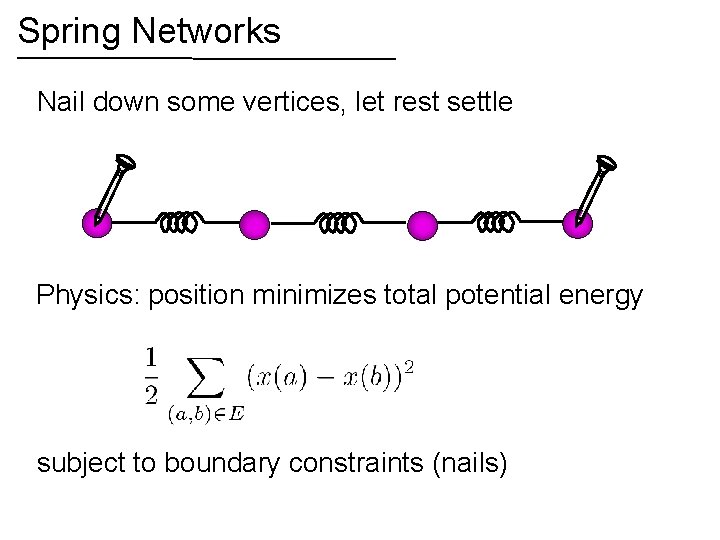
Spring Networks Nail down some vertices, let rest settle Physics: position minimizes total potential energy subject to boundary constraints (nails)

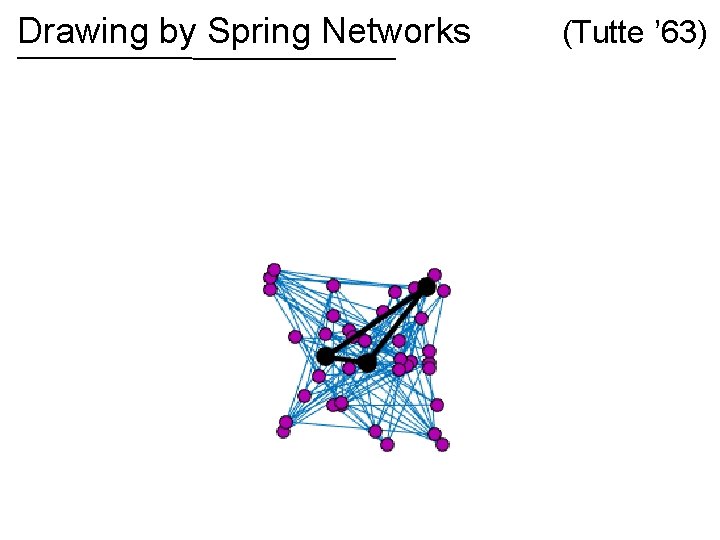
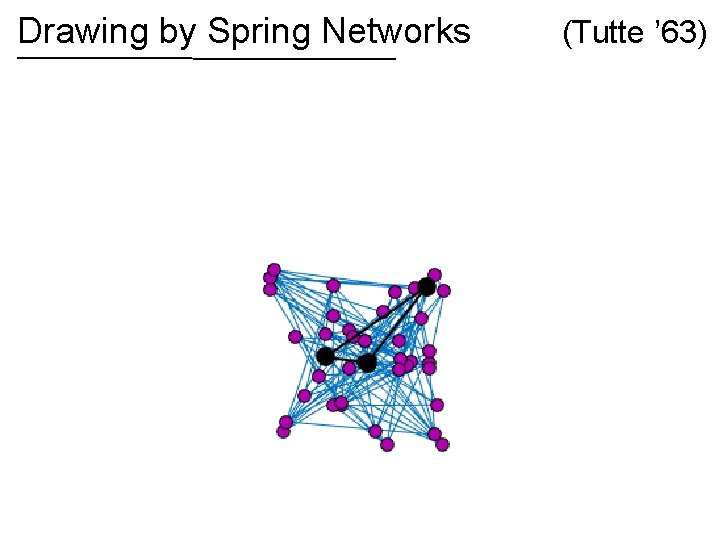
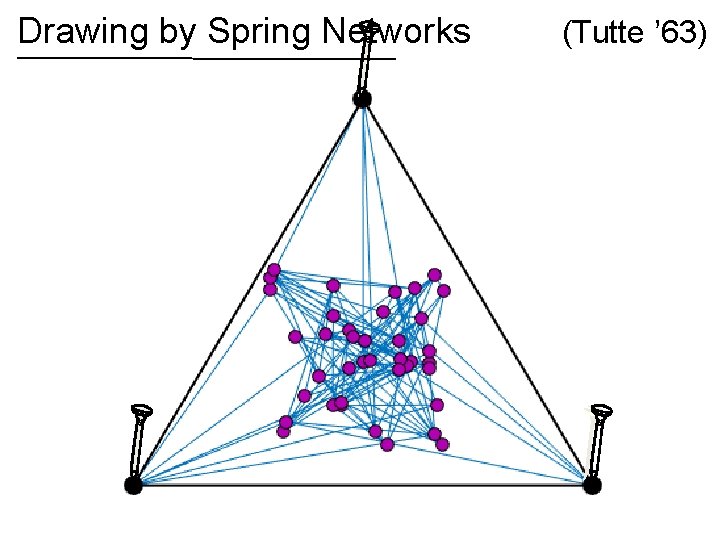
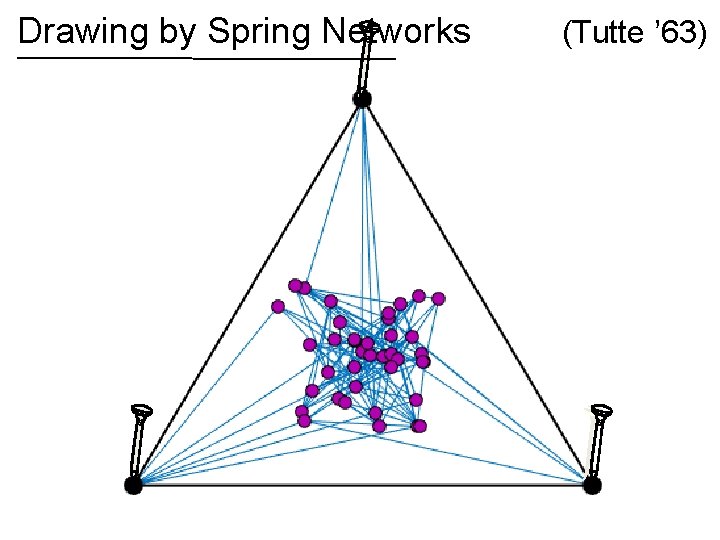
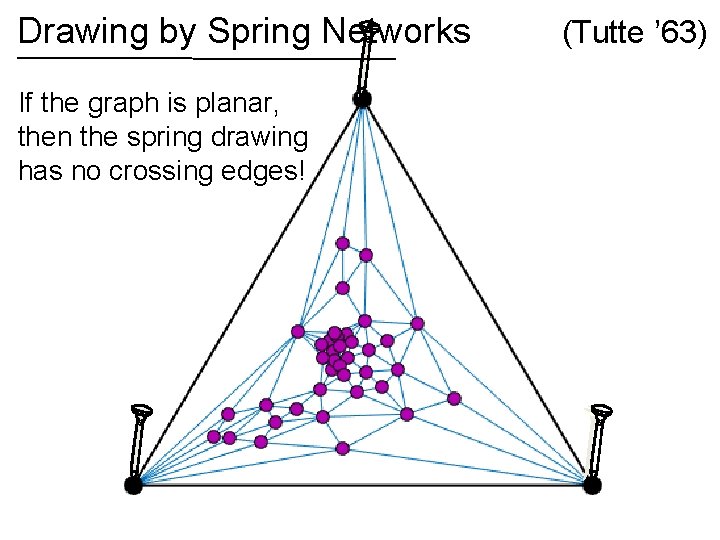
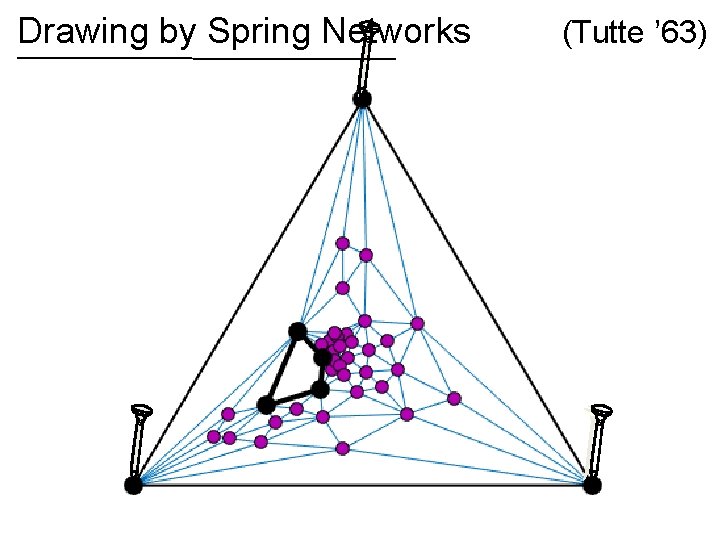
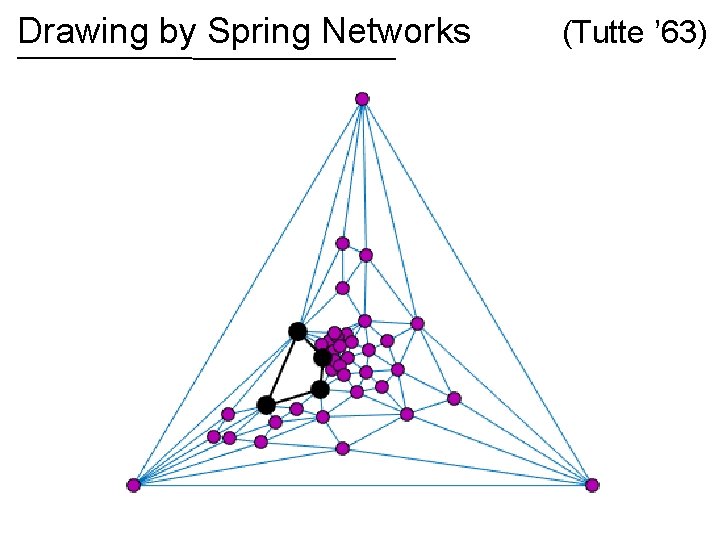
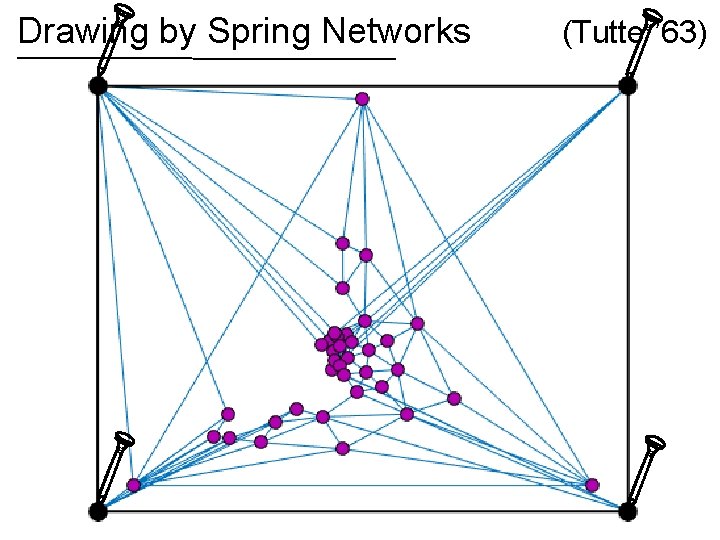
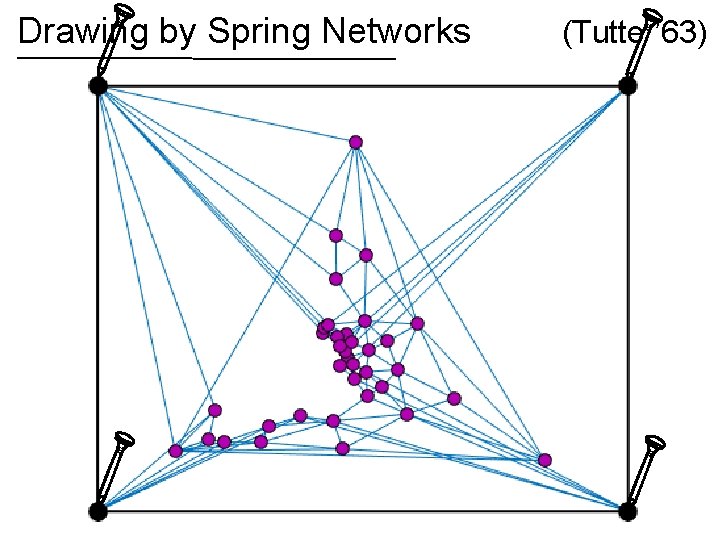
Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

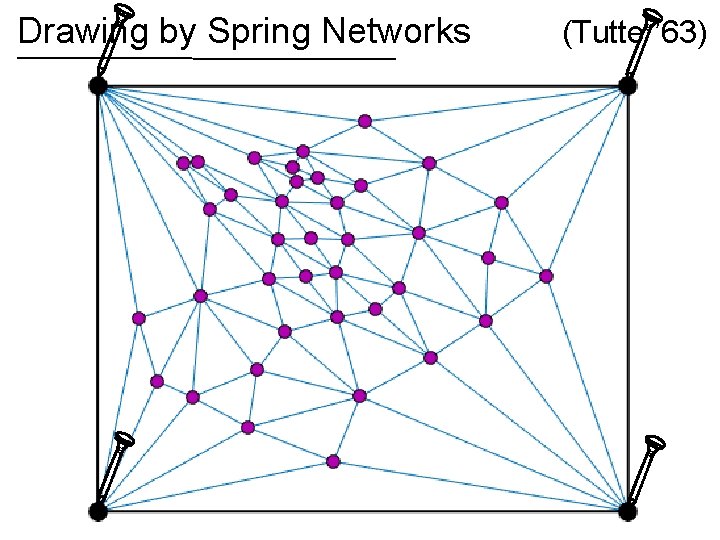
Drawing by Spring Networks If the graph is planar, then the spring drawing has no crossing edges! (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Drawing by Spring Networks (Tutte ’ 63)

Spectral Graph Theory A n-by-n symmetric matrix has n real eigenvalues and eigenvectors such that These eigenvalues and eigenvectors tell us a lot about a graph!

Spectral Graph Theory A n-by-n symmetric matrix has n real eigenvalues and eigenvectors such that These eigenvalues and eigenvectors tell us a lot about a graph! (excluding )

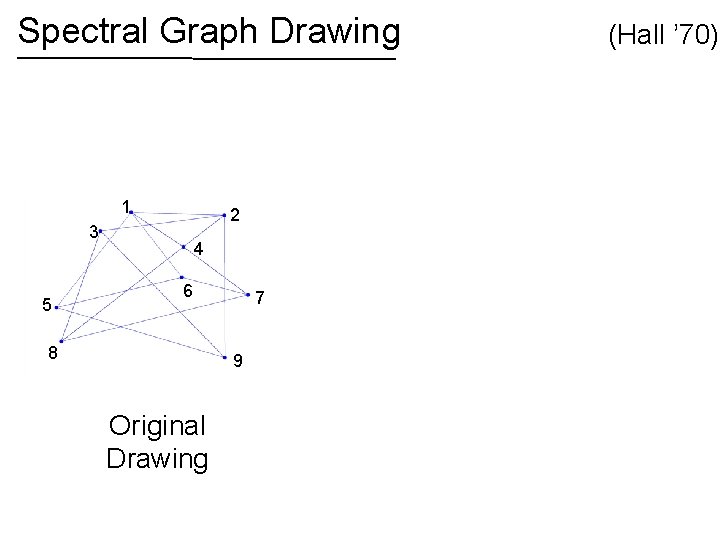
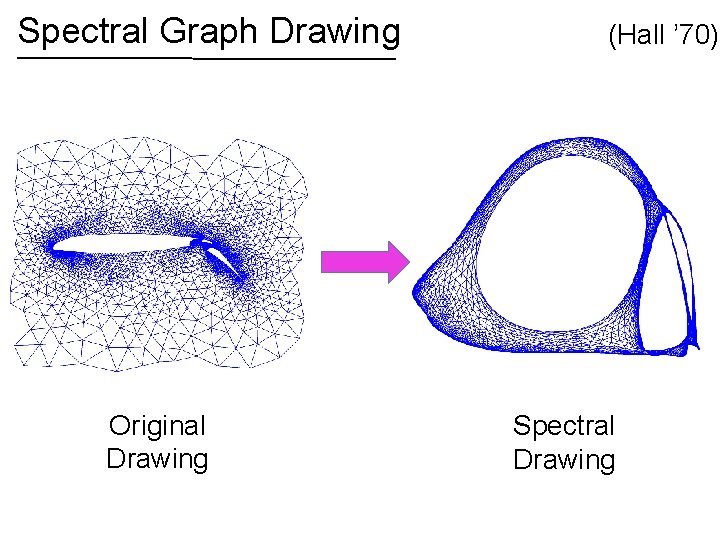
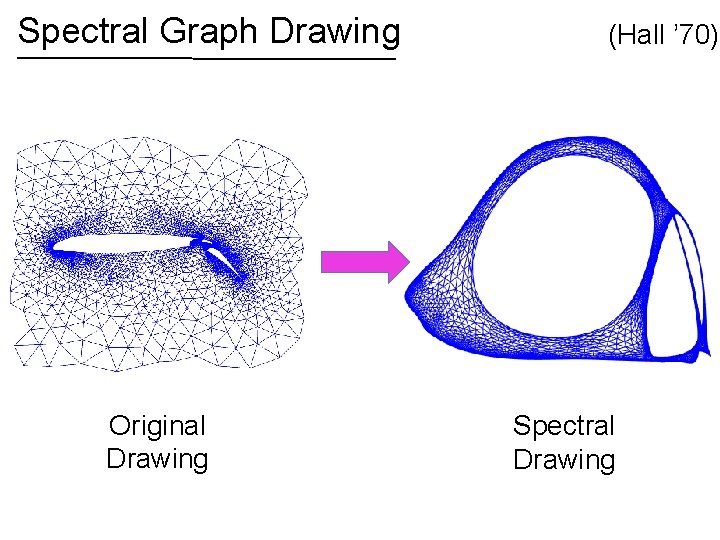
Spectral Graph Drawing 1 2 3 5 4 6 8 7 9 Original Drawing (Hall ’ 70)

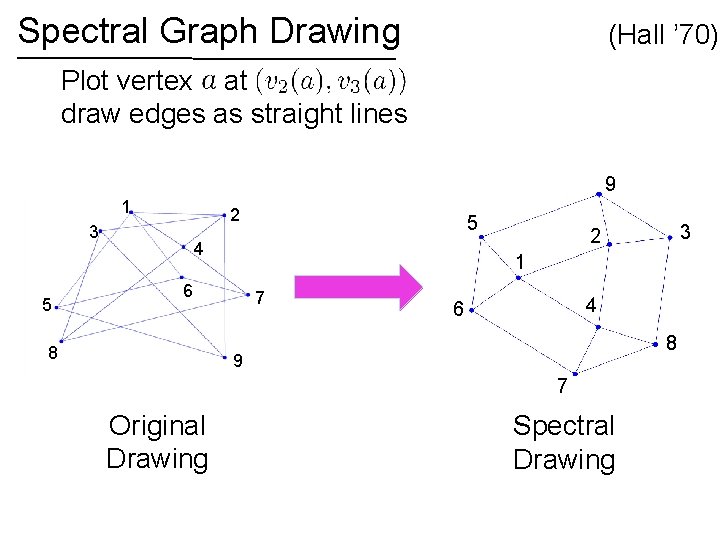
Spectral Graph Drawing (Hall ’ 70) Plot vertex at draw edges as straight lines 9 1 2 3 5 5 4 1 6 8 7 4 6 8 9 7 Original Drawing 3 2 Spectral Drawing

Spectral Graph Drawing Original Drawing (Hall ’ 70) Spectral Drawing

Spectral Graph Drawing Original Drawing (Hall ’ 70) Spectral Drawing

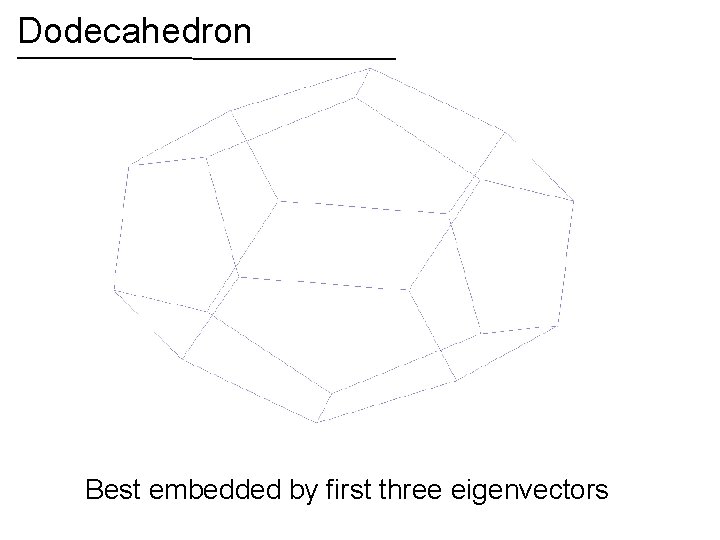
Dodecahedron Best embedded by first three eigenvectors

Erdos’s co-authorship graph

When there is a “nice” drawing Most edges are short Vertices are spread out and don’t clump too much is close to 0 When is big, say there is no nice picture of the graph

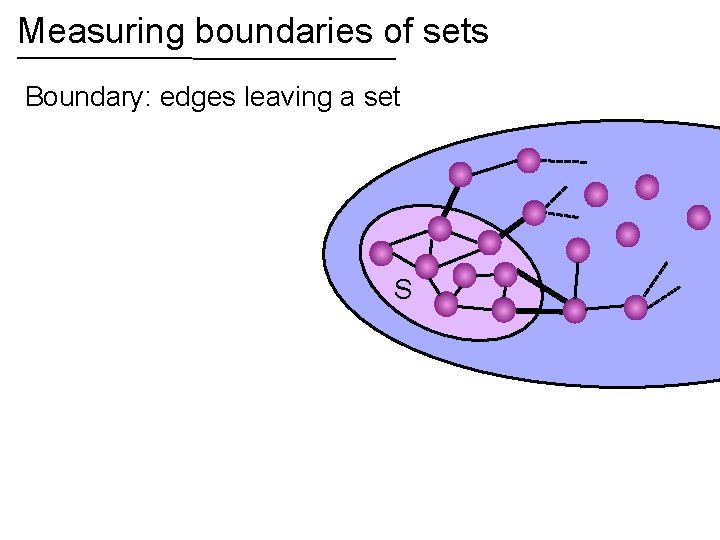
Measuring boundaries of sets Boundary: edges leaving a set S S

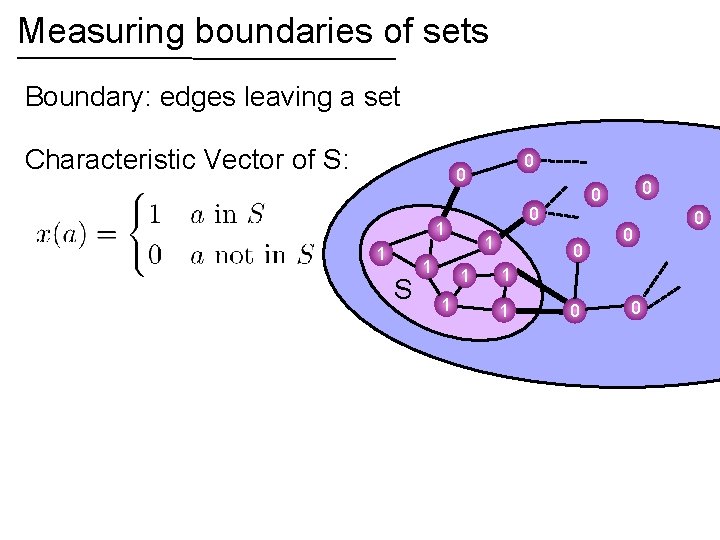
Measuring boundaries of sets Boundary: edges leaving a set Characteristic Vector of S: 0 0 0 1 1 S S 1 1 0 0 0

Measuring boundaries of sets Boundary: edges leaving a set Characteristic Vector of S: 0 0 0 1 1 S S 1 1 0 0 0

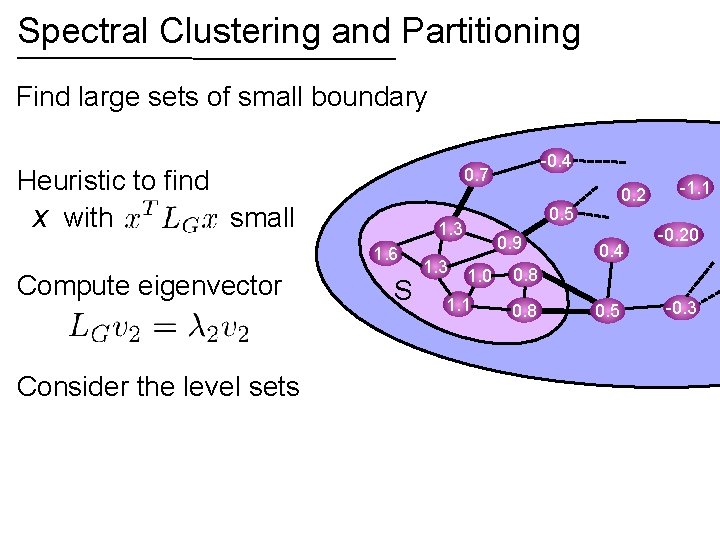
Spectral Clustering and Partitioning Find large sets of small boundary Heuristic to find x with small 0. 7 Consider the level sets S S 1. 3 0. 2 0. 5 1. 3 1. 6 Compute eigenvector -0. 4 0. 9 1. 0 1. 1 0. 4 -1. 1 -0. 20 0. 8 0. 5 -0. 3

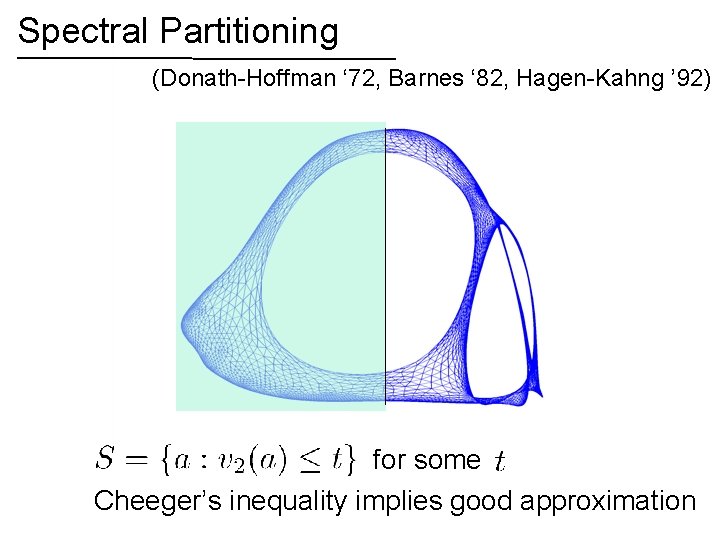
Spectral Partitioning (Donath-Hoffman ‘ 72, Barnes ‘ 82, Hagen-Kahng ’ 92) for some Cheeger’s inequality implies good approximation

Spectral Partitioning (Donath-Hoffman ‘ 72, Barnes ‘ 82, Hagen-Kahng ’ 92) for some Cheeger’s inequality implies good approximation

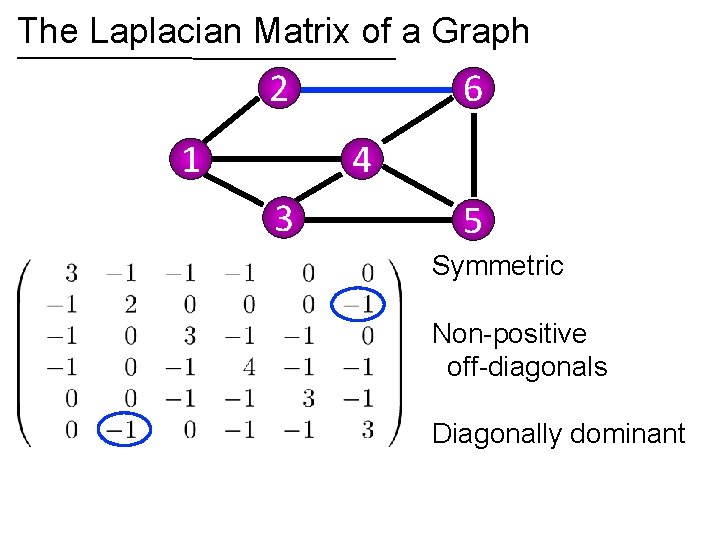
The Laplacian Matrix of a Graph 2 1 6 4 3 5 Symmetric Non-positive off-diagonals Diagonally dominant
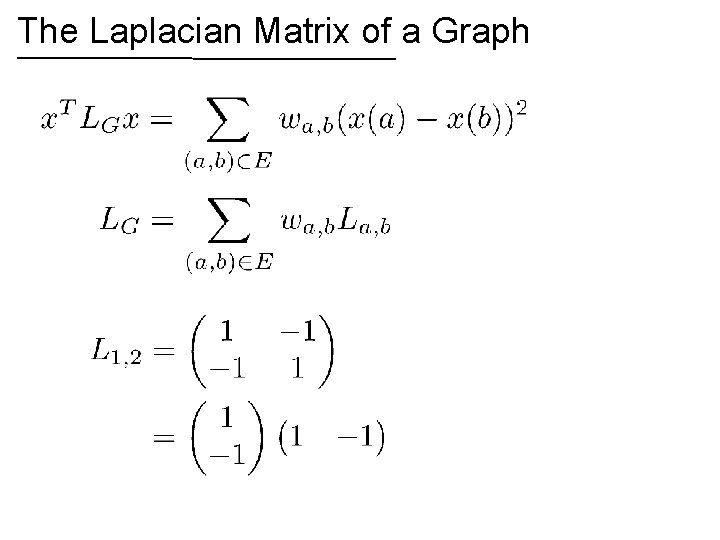
The Laplacian Matrix of a Graph

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers Where m is number of non-zeros and n is dimension

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers Koutis, Miller, Peng ’ 11: Low-stretch trees and sampling Where m is number of non-zeros and n is dimension

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers Koutis, Miller, Peng ’ 11: Low-stretch trees and sampling Cohen, Kyng, Pachocki, Peng, Rao ’ 14: Where m is number of non-zeros and n is dimension

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers Koutis, Miller, Peng ’ 11: Low-stretch trees and sampling Cohen, Kyng, Pachocki, Peng, Rao ’ 14: Good code: LAMG (lean algebraic multigrid) – Livne-Brandt CMG (combinatorial multigrid) – Koutis

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers An -accurate solution to is an satisfying where

Quickly Solving Laplacian Equations S, Teng ’ 04: Using low-stretch trees and sparsifiers An -accurate solution to is an satisfying Allows fast computation of eigenvectors corresponding to small eigenvalues.

Laplacians in Linear Programming Laplacians appear when solving Linear Programs on on graphs by Interior Point Methods Maximum and Min-Cost Flow Shortest Paths Isotonic Regression (Daitch, S ’ 08, Mądry ‘ 13) (Cohen, Mądry, Sankowski, Vladu ‘ 16) (Kyng, Rao, Sachdeva ‘ 15) Lipschitz Learning : regularized interpolation on graphs (Kyng, Rao, Sachdeva, S ‘ 15)

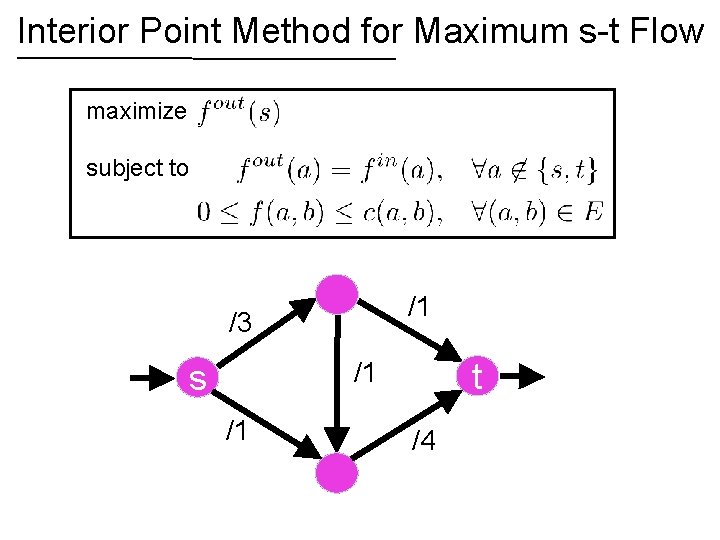
Interior Point Method for Maximum s-t Flow maximize subject to /1 /3 t /1 s /1 /4

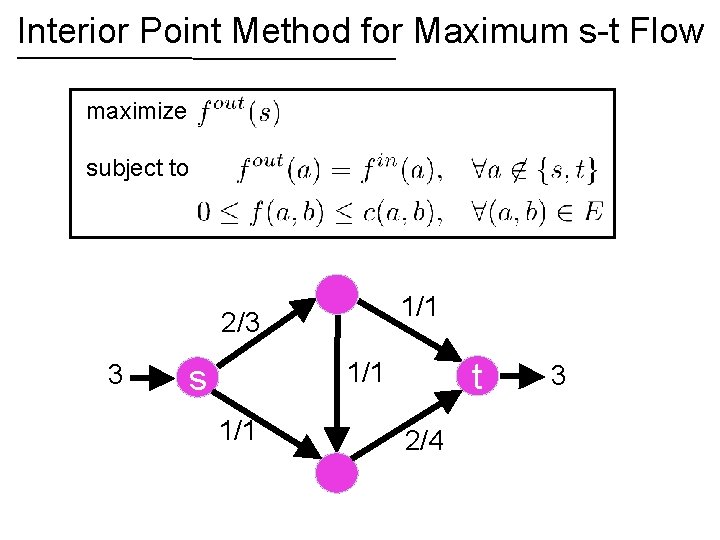
Interior Point Method for Maximum s-t Flow maximize subject to 1/1 2/3 3 t 1/1 s 1/1 2/4 3

Interior Point Method for Maximum s-t Flow maximize subject to Multiple calls with varying weights maximize subject to

Spectral Sparsification Every graph can be approximated by a sparse graph with a similar Laplacian

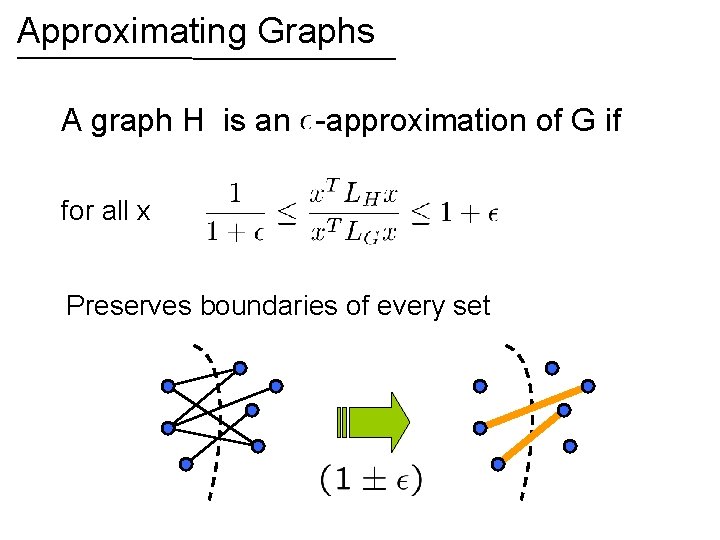
Approximating Graphs A graph H is an -approximation of G if for all x

Approximating Graphs A graph H is an -approximation of G if for all x Preserves boundaries of every set

Approximating Graphs A graph H is an -approximation of G if for all x Solutions to linear equations are similar As are effective resistances

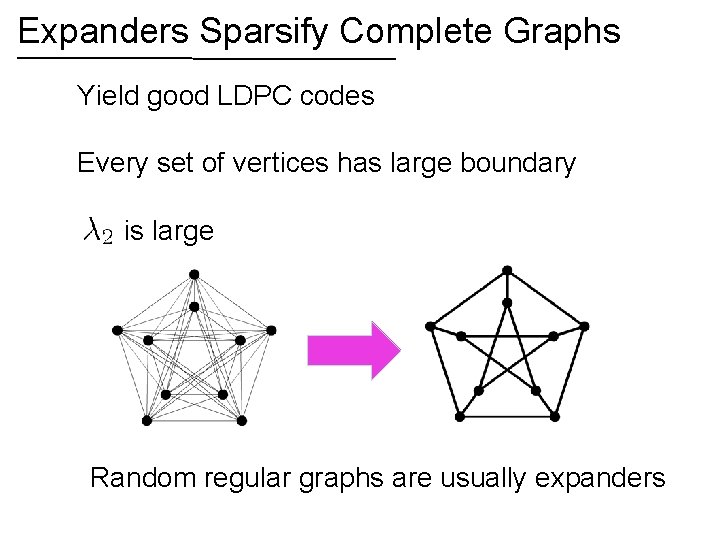
Expanders Sparsify Complete Graphs Yield good LDPC codes Every set of vertices has large boundary is large Random regular graphs are usually expanders

Sparsification by Random Sampling Assign a probability pa, b to each edge (a, b) Include edge (a, b) in H with probability pa, b. If include edge (a, b), give it weight wa, b /pa, b

Sparsification by Random Sampling Choose pa, b to be wa, b times the effective resistance between a and b. Low resistance between a and b means there are many alternate routes for current to flow and that the edge is not critical. Proof by random matrix concentration bounds (Rudelson, Ahlswede-Winter, Tropp, etc. ) Only need edges (S, Srivastava ‘ 08)

Optimal Graph Sparsification? For every , there is a s. t. and Is within a factor of 2 of how well Ramanujan expanders approximate complete graphs (Batson, S, Srivastava ‘ 09)

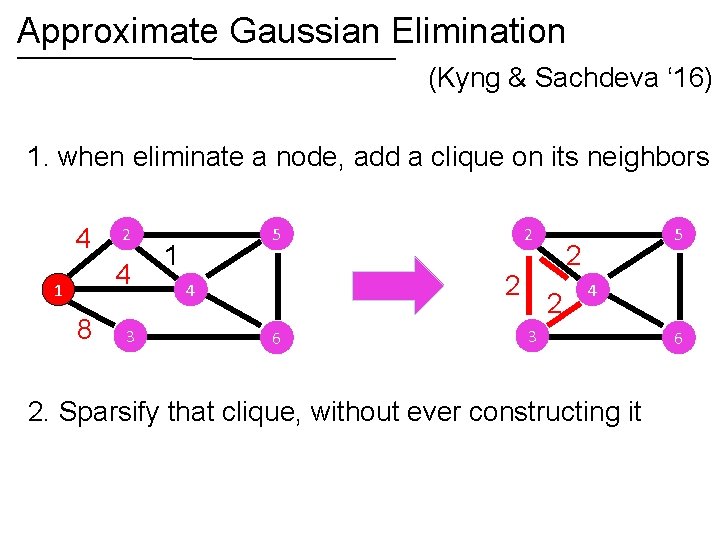
Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) Gaussian Elimination: compute upper triangular U so that Approximate Gaussian Elimination: compute sparse upper triangular U so that

Additive view of Gaussian Elimination •

Additive view of Gaussian Elimination Find the rank-1 matrix that agrees on the first row and column.

Additive view of Gaussian Elimination Subtract the rank 1 matrix. We have eliminated the first variable.

Additive view of Gaussian Elimination

Additive view of Gaussian Elimination Find the rank-1 matrix that agrees on the next row and column.

Additive view of Gaussian Elimination Subtract the rank 1 matrix. We have eliminated the second variable.

Additive view of Gaussian Elimination Running time proportional to sum of squares of number of non-zeros in these vectors.

Additive view of Gaussian Elimination

Additive view of Gaussian Elimination

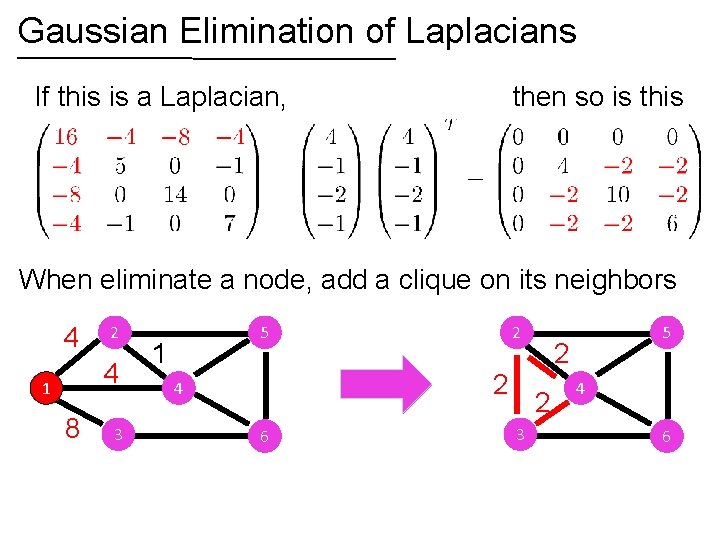
Gaussian Elimination of Laplacians If this is a Laplacian, then so is this

Gaussian Elimination of Laplacians If this is a Laplacian, then so is this When eliminate a node, add a clique on its neighbors 4 2 4 1 8 3 5 1 2 2 4 6 2 2 3 5 4 6

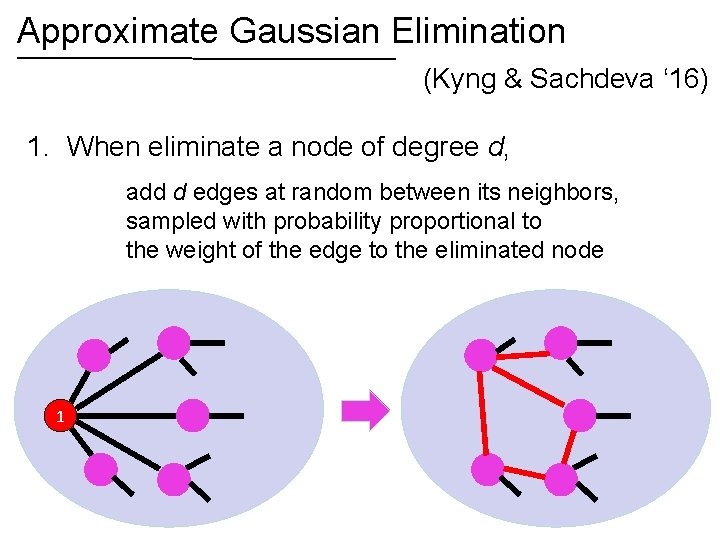
Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) 1. when eliminate a node, add a clique on its neighbors 4 2 4 1 8 3 5 1 2 2 4 6 5 2 2 4 3 2. Sparsify that clique, without ever constructing it 6

Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) 1. When eliminate a node of degree d, add d edges at random between its neighbors, sampled with probability proportional to the weight of the edge to the eliminated node 1

Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) 0. Initialize by randomly permuting vertices, and making copies of every edge 1. When eliminate a node of degree d, add d edges at random between its neighbors, sampled with probability proportional to the weight of the edge to the eliminated node Total time is

Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) 0. Initialize by randomly permuting vertices, and making copies of every edge 1. When eliminate a node of degree d, add d edges at random between its neighbors, sampled with probability proportional to the weight of the edge to the eliminated node Total time is Can be improved by sacrificing some simplicity

Approximate Gaussian Elimination (Kyng & Sachdeva ‘ 16) Analysis by Random Matrix Theory: Write UTU as a sum of random matrices. Random permutation and copying control the variances of the random matrices Apply Matrix Freedman inequality (Tropp ‘ 11)

Recent Developments Other families of linear systems (Kyng, Lee, Peng, Sachdeva, S ‘ 16) complex-weighted Laplacians connection Laplacians. jl

To learn more My web page on: Laplacian linear equations, sparsification, local graph clustering, low-stretch spanning trees, and so on. My class notes from “Graphs and Networks” and “Spectral Graph Theory” Lx = b, by Nisheeth Vishnoi
 Spectral graph theory and its applications
Spectral graph theory and its applications Ingrid spielman
Ingrid spielman Stephanie spielman osu
Stephanie spielman osu Spectral graph theory spielman
Spectral graph theory spielman G = (v e)
G = (v e) Laplacian operator
Laplacian operator Laplacian of gaussian
Laplacian of gaussian Laplacian filter
Laplacian filter Lnxn
Lnxn Definition of a conservative vector field
Definition of a conservative vector field Graph laplacian regularization
Graph laplacian regularization Laplace transfer function table
Laplace transfer function table Laplace equation spherical
Laplace equation spherical Laplacian operator
Laplacian operator Project outline
Project outline Laplacian of gaussian
Laplacian of gaussian Laplacian of a vector
Laplacian of a vector Polynomial function form
Polynomial function form State graphs in software testing
State graphs in software testing Comparing distance/time graphs to speed/time graphs
Comparing distance/time graphs to speed/time graphs Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Cái miệng nó xinh thế
Cái miệng nó xinh thế Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Bổ thể
Bổ thể Tư thế ngồi viết
Tư thế ngồi viết Thẻ vin
Thẻ vin Ví dụ về giọng cùng tên
Ví dụ về giọng cùng tên Thể thơ truyền thống
Thể thơ truyền thống Hát lên người ơi alleluia
Hát lên người ơi alleluia Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Phép trừ bù
Phép trừ bù Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tiính động năng
Công thức tiính động năng Các môn thể thao bắt đầu bằng từ đua
Các môn thể thao bắt đầu bằng từ đua Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Slidetodoc
Slidetodoc Số nguyên tố là
Số nguyên tố là Tia chieu sa te
Tia chieu sa te đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Chụp phim tư thế worms-breton
Chụp phim tư thế worms-breton Hệ hô hấp
Hệ hô hấp ưu thế lai là gì
ưu thế lai là gì Tư thế ngồi viết
Tư thế ngồi viết Vectors and matrices
Vectors and matrices Dr frost matrices
Dr frost matrices Matrices simultaneous equations worksheet
Matrices simultaneous equations worksheet Clasificacion de matrices
Clasificacion de matrices Unit 1 algebra basics homework 6 matrices
Unit 1 algebra basics homework 6 matrices Igualdad de matriz
Igualdad de matriz Matrices 2 bachillerato
Matrices 2 bachillerato Google docs matrices
Google docs matrices Matrix transpose times matrix
Matrix transpose times matrix Matrices diagonal
Matrices diagonal Leslie matrix
Leslie matrix Distance matrices
Distance matrices Matriz nxm
Matriz nxm Matrix multiplication associative property
Matrix multiplication associative property Stata vector
Stata vector Vectores y matrices en java
Vectores y matrices en java Subtract matrices calculator
Subtract matrices calculator Matrices
Matrices Eigenvectors for dummies
Eigenvectors for dummies