Partitional Clustering Partition n objects into k clusters

Partitional Clustering Partition n objects into k clusters These techniques start with K clusters (partitions) The partitions (clusters) is decided in advance by the user. 2 12 March 2021 במתמטיקה סמינריון ביולוגית במתמטיקה סמינריון

k-medoid methods There are two best-known k-medoid methods: 1. 2. 3 3/12/2021 PAM (Partitioning Around Medoids) CLARA (Clustering LARge Applications) סמינריון במתמטיקה ביולוגית

PAM (Partitioning Around Medoids) The Idea: Find a single partition of the data into K clusters Each cluster has a most representative point a point that is the most “centrally” located point in the cluster with respect to some measure, e. g. , distance. These lead us to the medoid definition… 4 12 March 2021 במתמטיקה סמינריון ביולוגית במתמטיקה סמינריון

Medoid - definition A medoid is an actual point in the dataset that is centrally located and is therefore representative of the cluster. 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 0 0 0 5 3/12/2021 1 2 3 4 5 6 7 8 9 10 0 סמינריון במתמטיקה ביולוגית 1 2 3 4 5 6 7 8 9 10

More precisely… Object Oj belongs to the cluster represented by Om if: d (Oj, Om) = min. Oe d (Oj, Oe) Oj is a non-selected object Om is a (selected) medoid d(O 1, O 2) denotes the dissimilarity or distance between objects O 1 and O 2. min. Oe denotes the minimum over all medoids Oe 6 3/12/2021 סמינריון במתמטיקה ביולוגית

PAM – In General… To find the k-medoids… PAM begins with an arbitrary selection of k objects. Then, in each step, a swap between a selected object Om and a non-selected object Op is made. As long as such a swap would result in an improvement of the quality of the clustering. 7 3/12/2021 סמינריון במתמטיקה ביולוגית

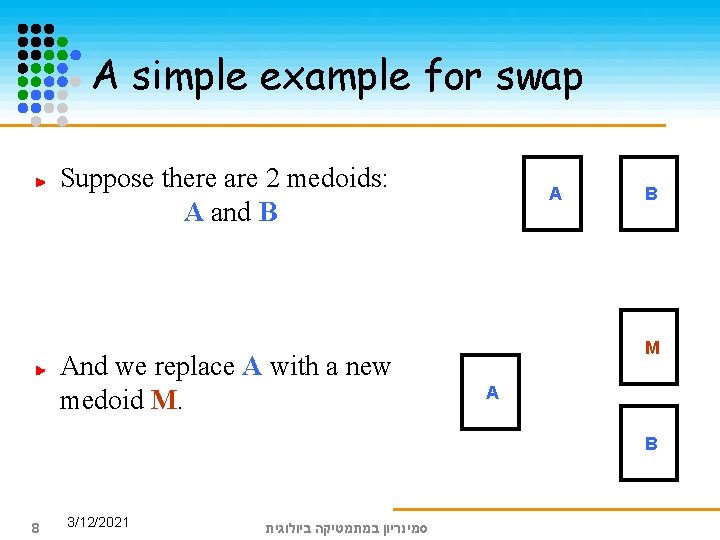
A simple example for swap Suppose there are 2 medoids: A and B And we replace A with a new medoid M. A B M A B 8 3/12/2021 סמינריון במתמטיקה ביולוגית

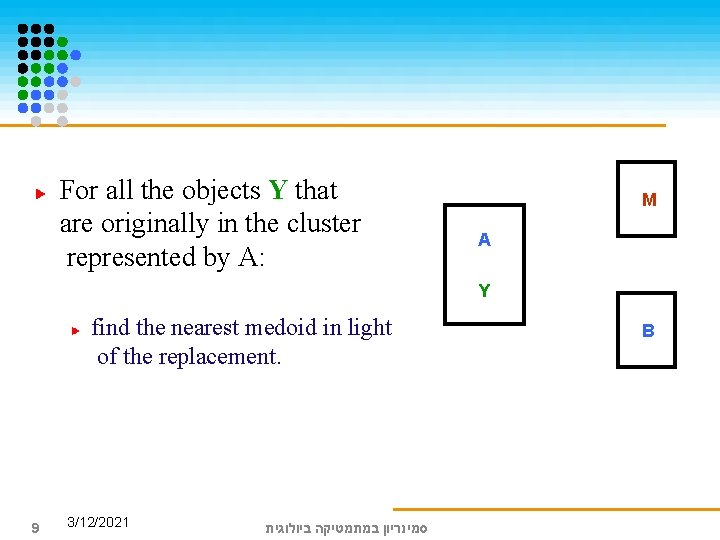
For all the objects Y that are originally in the cluster represented by A: M A Y find the nearest medoid in light of the replacement. 9 3/12/2021 סמינריון במתמטיקה ביולוגית B

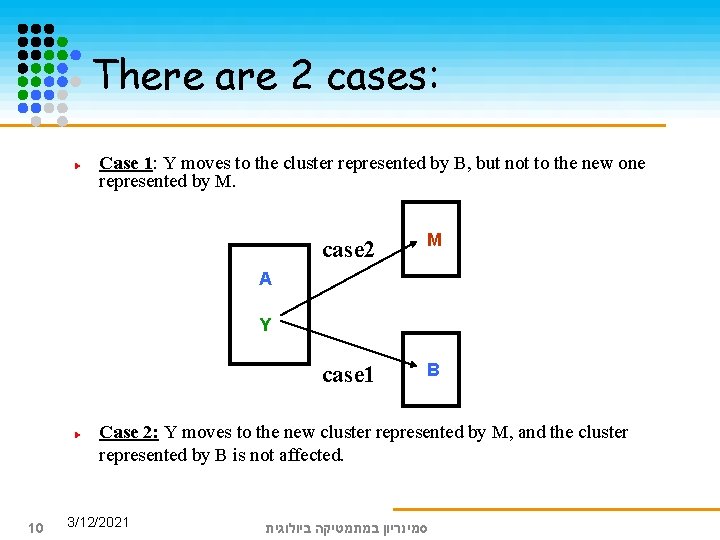
There are 2 cases: Case 1: Y moves to the cluster represented by B, but not to the new one represented by M. case 2 M case 1 B A Y Case 2: Y moves to the new cluster represented by M, and the cluster represented by B is not affected. 10 3/12/2021 סמינריון במתמטיקה ביולוגית

We also need to consider all the objects Z that are originally in B’s cluster. M A Z B 11 3/12/2021 סמינריון במתמטיקה ביולוגית

More 2 cases: Case 3: Z either stays with B Case 4: Z moves to the new cluster represented by M. M case 4 A Z case 3 12 3/12/2021 B סמינריון במתמטיקה ביולוגית

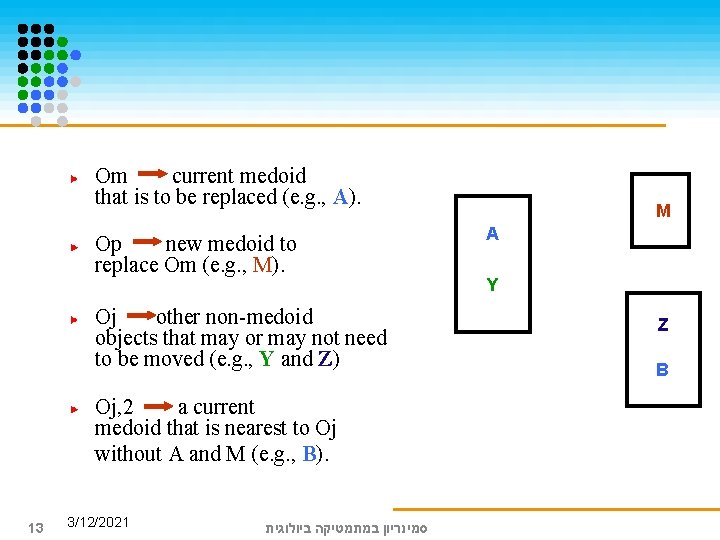
Om current medoid that is to be replaced (e. g. , A). Op new medoid to replace Om (e. g. , M). Oj other non-medoid objects that may or may not need to be moved (e. g. , Y and Z) Oj, 2 a current medoid that is nearest to Oj without A and M (e. g. , B). 13 3/12/2021 סמינריון במתמטיקה ביולוגית M A Y Z B

To formalize the effect of a swap between Om and Op, PAM computes costs Cjmp for all non-medoid objects Oj. Depending on which of the following cases Oj is in, Cjmp is defined differently. 14 3/12/2021 סמינריון במתמטיקה ביולוגית

Case 1: Oj currently belongs to the cluster represented by Om. Oj be more similar to Oj, 2 than to Op, i. e , . d(Oj, Op) >= d(Oj, 2) Thus, Oj would belong to the cluster represented by Oj, 2 The cost of the swap is: Cjmp = d(Oj, 2) – d(Oj, Om) 15 3/12/2021 סמינריון במתמטיקה ביולוגית Oj Oj, 2 Om Op

Case 2: Oj currently belongs to the cluster represented by Om. Oj is less similar to Oj, 2 than to Op, i. e , . d(Oj, Op) < d(Oj, 2) Thus, Oj would belong to the cluster represented by Op The cost of the swap is: Cjmp = d(Oj, Op) – d(Oj, Om) 16 3/12/2021 סמינריון במתמטיקה ביולוגית Oj Oj, 2 Om Op

Case 3: Oj currently belongs to a cluster Oj, 2. Oj Oj is more similar to Oj, 2 than to Op. Then, even if Om is replaced by Op, Oj would stay in the cluster represented by Oj, 2. The cost is: Cjmp = 0 17 3/12/2021 סמינריון במתמטיקה ביולוגית Om Oj, 2 Op

Case 4: Oj currently belongs to the cluster represented by Oj, 2. Oj is less similar to Oj, 2 than to Op. Oj Oj, 2 Om Op Then, replacing Om with Op would cause Oj to jump to the cluster of Op from that of Oj. The cost of the swap is: Cjmp = d(Oj, Op) – d(Oj, 2) 18 3/12/2021 סמינריון במתמטיקה ביולוגית

Total Cost Combining the four cases , the Total Cost of replacing O TCmp = 19 3/12/2021 סמינריון במתמטיקה ביולוגית

Algorithm PAM Arbitrarily choose k objects as the initial medoids Until no change, do (Re) assign each object to the cluster to which the nearest medoid Randomly select a non-medoid object Op, compute the total cost, TCmp, of swapping medoid Om with Op If TCmp < 0 then swap Om with Op to form the new set of k medoids 20 3/12/2021 סמינריון במתמטיקה ביולוגית

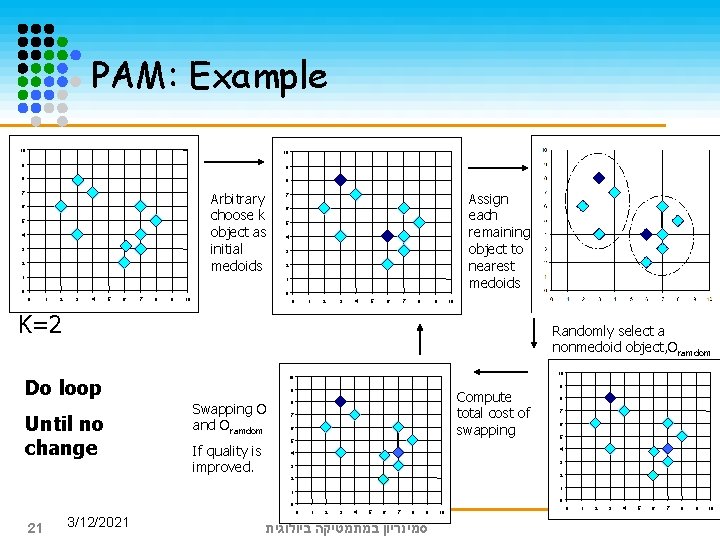
PAM: Example 10 10 9 9 8 8 Arbitrary choose k object as initial medoids 7 6 5 4 3 2 1 Assign each remaining object to nearest medoids 7 6 5 4 3 2 1 0 0 0 1 2 3 4 5 6 7 8 9 10 K=2 Randomly select a nonmedoid object, Oramdom Do loop Until no change 10 10 9 Swapping O and Oramdom If quality is improved. Compute total cost of swapping 8 7 6 5 3 3 2 1 1 0 0 3/12/2021 8 4 4 2 21 9 0 1 2 3 4 5 6 7 8 9 סמינריון במתמטיקה ביולוגית 10 0 1 2 3 4 5 6 7 8 9 10

PAM Disadvantage Experimental results show that PAM works satisfactorily for small data sets (e. g. , 100 objects in 5 clusters). But, it is not efficient in dealing with medium and large data sets. This is not too surprising if we perform a complexity analysis on PAM. There altogether k(n-k) pairs. For each pair, computing TCmp requires the examination of (n - k) nonselected objects. Thus, the complexity combined is of . And this is the complexity of only one iteration. Thus, it is obvious that PAM becomes too costly for large values of n and k. This analysis motivates the development of CLARA. 26 3/12/2021 סמינריון במתמטיקה ביולוגית

CLARA (Clustering LARge Applications) Designed to handle large data sets The Idea: Instead of finding representative objects for the entire data set, CLARA draws a sample of the data set, applies PAM on the sample, and finds the medoids of the sample. The point is that, if the sample is drawn in a sufficiently random way, the medoids of the sample would approximate the medoids of the entire data set. 27 3/12/2021 סמינריון במתמטיקה ביולוגית

To come up with better approximations, CLARA draws multiple samples and gives the best clustering as the output. The quality of a clustering is measured based on the average dissimilarity of all objects in the entire data set. Experiments shows that samples of size 40 + 2 K give satisfactory results. 28 3/12/2021 סמינריון במתמטיקה ביולוגית

Algorithm CLARA For i = 1 to 5, repeat the following steps: Draw a sample of 402 + k objects randomly from the entire data set, and call Algorithm PAM to find k medoids of the sample. For each object Oj in the entire data set, determine which of the k medoids is the most similar to Oj. Calculate the average dissimilarity of the clustering obtained in the previous step. If this value is less than the current minimum, use this value as the current minimum, and retain the k medoids found in Step 2 as the best set of medoids obtained so far. Return to Step 1 to start the next iteration. 29 3/12/2021 סמינריון במתמטיקה ביולוגית

Biological Application סמינריון במתמטיקה ביולוגית 3/12/2021

The Biological Problem Some facts… Recent advances of experimental techniques and automation in molecular and The number of structures deposited in the Protein Data Bank (PDB) is now o 31 3/12/2021 סמינריון במתמטיקה ביולוגית

Over half of all of the proteins of sequenced genomes has no inferable molecular functions. As sequence similarity infers functional similarity, structural similarity also infers similarity in molecular function: if a hypothetical protein has a structure similar to one or more protein structures of known function, the structural similarity infers a powerful clue to the molecular function of the hypothetical protein. Measures of structural similarity, assessed computationally or visually, between pairs of proteins are also the foundation for classifying protein structures. 32 3/12/2021 סמינריון במתמטיקה ביולוגית

The Goal The goal of the method is: To find measures of structural similarity between p We base our method on: distances 33 3/12/2021 סמינריון במתמטיקה ביולוגית

Some Biological Background… 3/12/2021 סמינריון במתמטיקה ביולוגית

Structure of the -Helix: sheet: 36 3/12/2021 סמינריון במתמטיקה ביולוגית

The Method We start with the distance matrix representation of protein structure. The distance matrix of a protein structure is a square matrix consisting o 38 3/12/2021 סמינריון במתמטיקה ביולוגית

When there are residues in protein p, its distance ma {dp(i, j): i, j=1, . . . , } dp(i, j) is the 39 3/12/2021 distance (in Å) between residues i an סמינריון במתמטיקה ביולוגית

We sub-divide the distance matrix of each protein structure into m The overlapping sub-matrices presenting local features involving m x m sub-matrices described by: 40 3/12/2021 סמינריון במתמטיקה ביולוגית

The collection of these sub-matrices over P proteins is: We use a collection of these sub-matrices from a large number of distance matrices to extract a set of K medoid sub-matrices by medoid analysis (PAM). 41 3/12/2021 סמינריון במתמטיקה ביולוגית

Example: 100 Medoids One hundred medoid sub-matrices obtained from partitioning around medoids (PAM) analysis of distance matrices of 100 sampled proteins. 42 3/12/2021 סמינריון במתמטיקה ביולוגית

Generation of the LFF Profile Each of the protein sub-matrices The count vector is labeled by the index of th summarizes the frequency distrib Any given protein structure can be represented by a profile, a vector of 43 3/12/2021 סמינריון במתמטיקה ביולוגית

We call this decoding process: profiling of the protein structure The final feature vector profile of protein p 44 3/12/2021 , סמינריון במתמטיקה ביולוגית

We normalize frequency of local interaction pattern k in 45 3/12/2021 סמינריון במתמטיקה ביולוגית

Normalization of the results Because the abundance of local patterns varies considerably from one pattern to another, some normalization of the profile is necessary. For example, the ‘‘null’’ pattern is most abundant of all, and, without normalization, such an abundant pattern will dominate when computing structural similarity or dissimilarity distances. This is not desirable because the frequency of the void pattern contains little structural information. 46 3/12/2021 סמינריון במתמטיקה ביולוגית

Normalize Vector Normalize vector X: . In our method: 47 3/12/2021 סמינריון במתמטיקה ביולוגית

Calculation of Similarity/ Dissimilarity Scores The profile of protein P: The collection of profiles, or the protein-bypattern matrix: 50 3/12/2021 סמינריון במתמטיקה ביולוגית

As a measure of structural similarity between two proteins p and q The cosine distance is defined as 1 - cos(Ap, Aq) and used to represent structural dissimilarity or st 51 3/12/2021 סמינריון במתמטיקה ביולוגית

Problem & Solution The Problem: The profile of protein P is a vector which belong to. The Solution: Using SVD which helps to reduce the number of dimensions. 52 3/12/2021 סמינריון במתמטיקה ביולוגית

Singular Value Decomposition (SVD) The SVD of matrix A is defined as U is an m x n matrix V is a n x n square matrix U, V are orthgonal so that: . Now we can approximating the original protein by pattern matrix by: 53 3/12/2021 סמינריון במתמטיקה ביולוגית

We compute the truncated SVD with k=3 to obtain approximation A 3 of the protein by pattern matrix, because the first three values are significantly greater than the rest. We can represent proteins and patterns in the same R 3 space by their first three principal coordinates: The 1 st -> length of protein The 2 nd -> types of secondary structure elements The 3 rd -> parallelism, direction 54 3/12/2021 סמינריון במתמטיקה ביולוגית

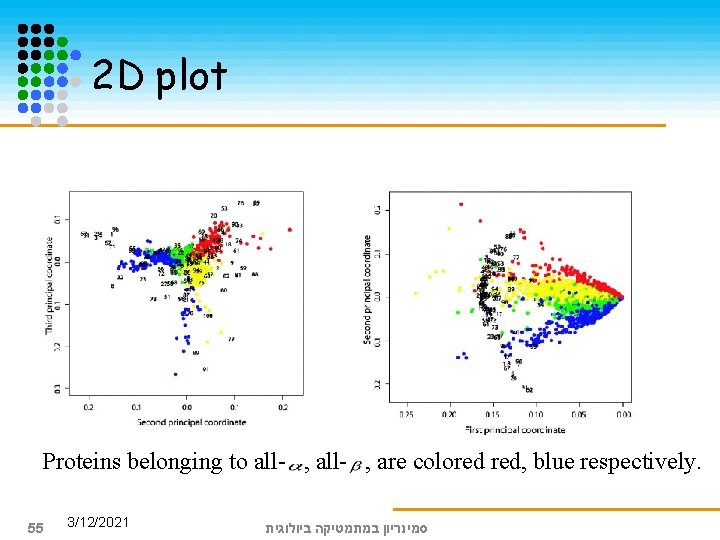
2 D plot Proteins belonging to all- , are colored red, blue respectively. 55 3/12/2021 סמינריון במתמטיקה ביולוגית

Criticism In order to find the k medoids… How many proteins should I use as my database? How should I choose the value of k, i. e. the number of the clusters? In order to find the overlapping sub-matrixes – how to choose the value for m? The method for finding structural similarity between proteins uses algorithm PAM which is not effective for using large databases. So, why not using the CLARA algorithm ? Is the method able to recognize small proteins or those with no distinct secondary structure elements in their topology? 57 3/12/2021 סמינריון במתמטיקה ביולוגית

Analogy to text analysis Document -> vector of word counts Protein structure = document Protein structure -> document Words -> different medoid sub-matrices 59 3/12/2021 סמינריון במתמטיקה ביולוגית

The quality of clustering of local features is difficult to discern because of the domination of the null medoid and low signal to noise ratio of the rest of the modoids (lower four plots). However, after normalization by the spread of the counts in each representative medoid, the similarity among LFF profiles within each family is evident. 60 3/12/2021 סמינריון במתמטיקה ביולוגית

****k-medoid advantages 1. Very robust to the existence of outliers (i. e. , data points that are very far away from the rest of the data points). 2. Clusters found by k-medoid methods do not depend on the order in which the objects are examined. 3. Experiments have shown that the k-medoid methods can handle very large data sets quite efficiently. 61 3/12/2021 סמינריון במתמטיקה ביולוגית

After converting each protein structure into a local feature frequency (LFF) profile, the fold similarity between a pair of proteins can be computed very easily as Euclidean distance or cosine distance between two corresponding LFF profile vectors. 62 3/12/2021 סמינריון במתמטיקה ביולוגית

The quality of a clustering The quality of the chosen medoids, is measured by the average dissimilarity or distance between an object and the medoid of its cluster. 63 3/12/2021 סמינריון במתמטיקה ביולוגית