Weyl Lectures Daniel A Spielman Yale University Sparsification

![Spectral Sparsification [S-Teng] Approximate any (weighted) graph by a sparse weighted graph. Graph Laplacian Spectral Sparsification [S-Teng] Approximate any (weighted) graph by a sparse weighted graph. Graph Laplacian](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-3.jpg)











![Spectral Sparsification [S-Teng] For an input graph G with n vertices, find a sparse Spectral Sparsification [S-Teng] For an input graph G with n vertices, find a sparse](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-16.jpg)





![Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak]](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-22.jpg)
![Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Cannot do better if n Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Cannot do better if n](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-23.jpg)
![Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Can we approximate every graph Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Can we approximate every graph](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-24.jpg)


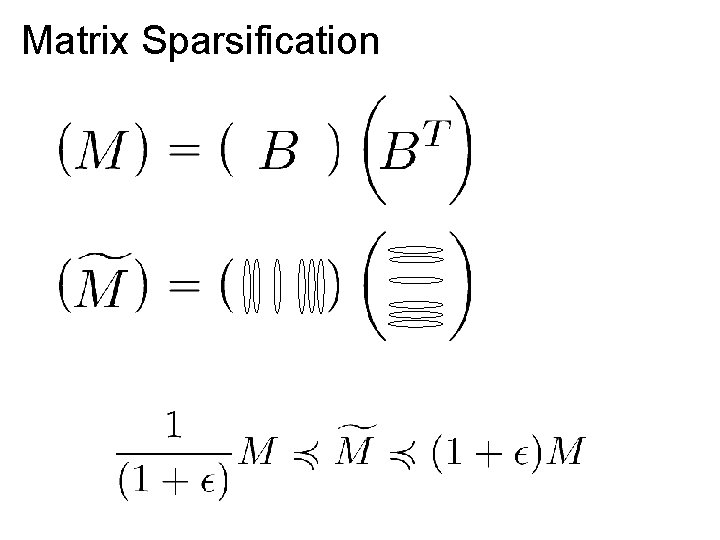



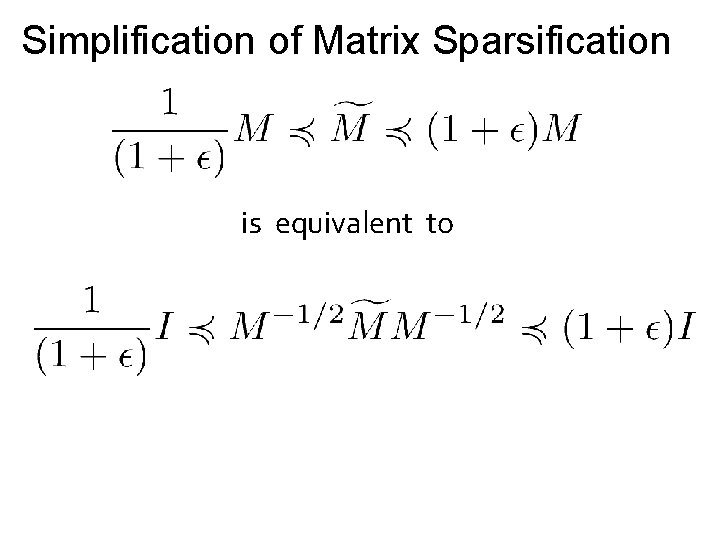

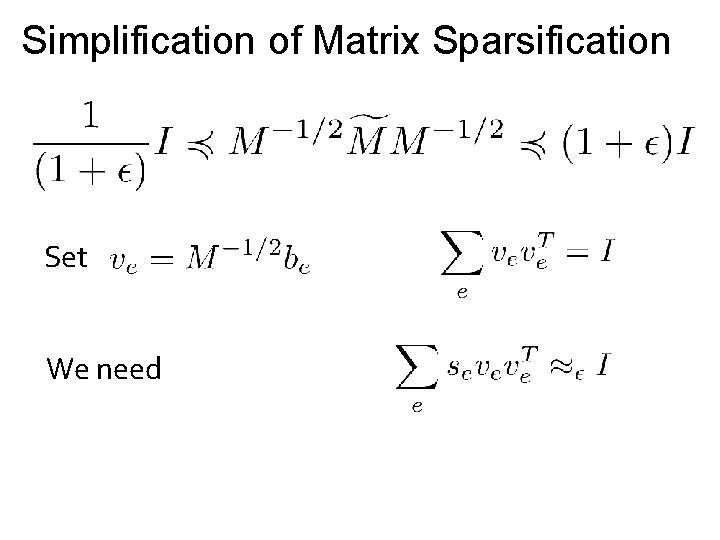


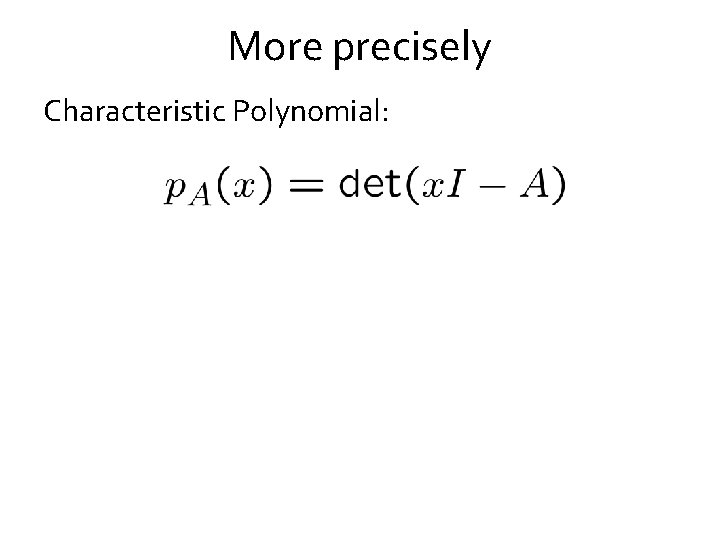


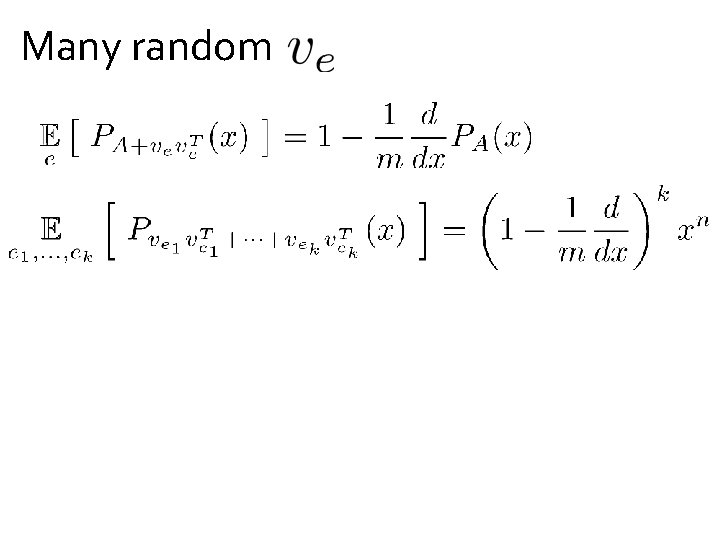









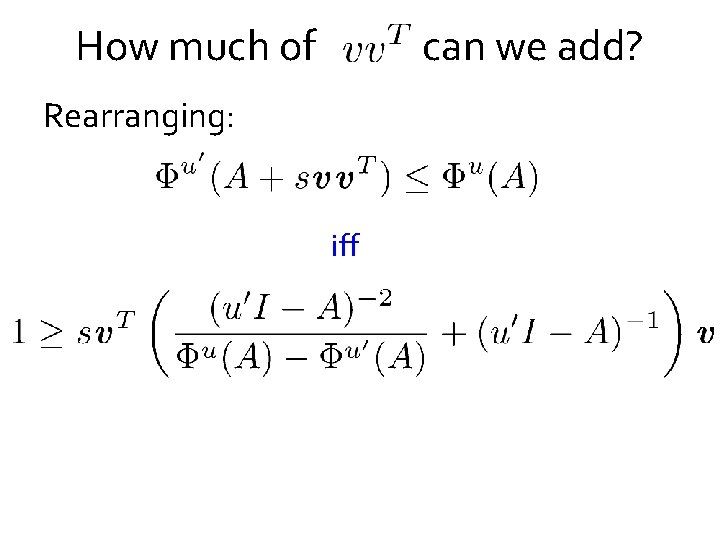
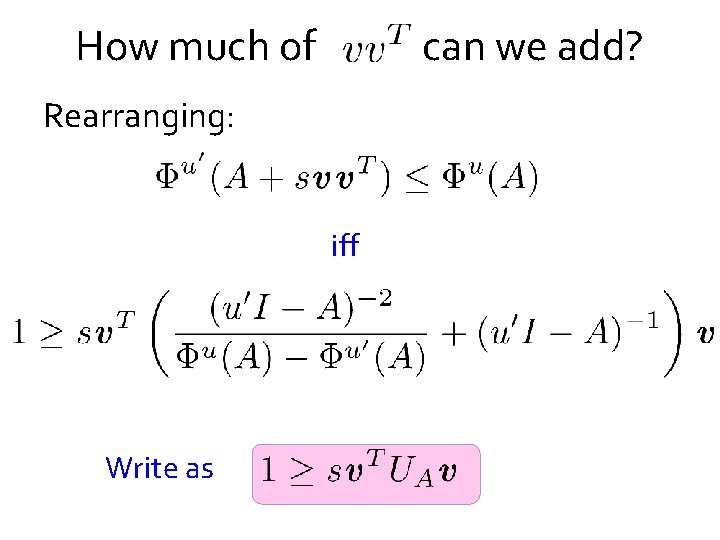













- Slides: 101

Weyl Lectures Daniel A. Spielman Yale University Sparsification of Graphs and Matrices The Solution of the Kadison-Singer Problem Ramanujan Graphs of Every Degree IAS, Nov 3, 2014

Sparsification of Graphs and Matrices joint work with Joshua Batson (MIT) Nikhil Srivastava (MSR India/Berkeley) Shang-Hua Teng (USC) IAS, Nov 3, 2014
![Spectral Sparsification STeng Approximate any weighted graph by a sparse weighted graph Graph Laplacian Spectral Sparsification [S-Teng] Approximate any (weighted) graph by a sparse weighted graph. Graph Laplacian](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-3.jpg)
Spectral Sparsification [S-Teng] Approximate any (weighted) graph by a sparse weighted graph. Graph Laplacian

Laplacian Quadratic Form, examples All edge-weights are 1

Laplacian Quadratic Form, examples All edge-weights are 1 Sum of squares of differences across edges

Laplacian Quadratic Form, examples All edge-weights are 1 Sum of squares of differences across edges

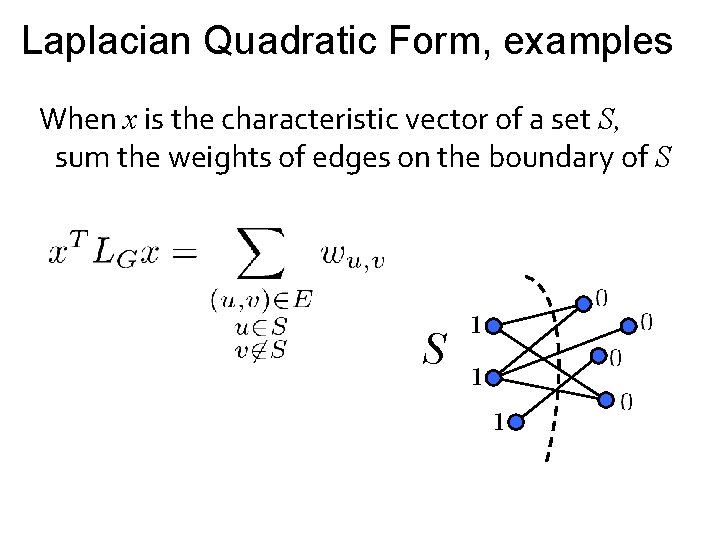
Laplacian Quadratic Form, examples When x is the characteristic vector of a set S, sum the weights of edges on the boundary of S S

Laplacian Matrices E. g.

Laplacian Matrices where Sum of outer products

Laplacian Matrices Positive semidefinite If connected, nullspace = Span(1)

Inequalities on Graphs and Matrices For matrices and for all if For graphs and if

Inequalities on Graphs and Matrices For matrices and for all if For graphs and if if

Approximations of Graphs and Matrices if For graphs and if

Approximations of Graphs and Matrices if For graphs and if That is, for all

Implications of Approximation LH and LG have similar eigenvalues Boundaries of sets are similar. Solutions to systems of linear equations are similar.
![Spectral Sparsification STeng For an input graph G with n vertices find a sparse Spectral Sparsification [S-Teng] For an input graph G with n vertices, find a sparse](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-16.jpg)
Spectral Sparsification [S-Teng] For an input graph G with n vertices, find a sparse graph H having so that edges

Approximations of Complete Graphs are Expanders: d-regular graphs on n vertices (n grows, d fixed) every set of vertices has large boundary random walks mix quickly incredibly useful

Approximations of Complete Graphs are Expanders: d-regular graphs on n vertices (n grows, d fixed) weak expanders: eigenvalues bounded from 0 strong expanders: all eigenvalues near d

Example: Approximating a Complete Graph For G the complete graph on n vertices all non-zero eigenvalues of LG are n. For ,

Example: Approximating a Complete Graph For G the complete graph on n vertices all non-zero eigenvalues of LG are n. For , For H a d-regular strong expander, all non-zero eigenvalues of LH are close to d. For ,

Example: Approximating a Complete Graph For G the complete graph on n vertices all non-zero eigenvalues of LG are n. For , For H a d-regular strong expander, all non-zero eigenvalues of LH are close to d. For , is a good approximation of
![Best Approximations of Complete Graphs Ramanujan Expanders Margulis LubotzkyPhillipsSarnak Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak]](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-22.jpg)
Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak]
![Best Approximations of Complete Graphs Ramanujan Expanders Margulis LubotzkyPhillipsSarnak Cannot do better if n Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Cannot do better if n](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-23.jpg)
Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Cannot do better if n grows while d is fixed [Alon-Boppana]
![Best Approximations of Complete Graphs Ramanujan Expanders Margulis LubotzkyPhillipsSarnak Can we approximate every graph Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Can we approximate every graph](https://slidetodoc.com/presentation_image_h/0d48fa3b0ad46c094d1f61bf8ca211c5/image-24.jpg)
Best Approximations of Complete Graphs Ramanujan Expanders [Margulis, Lubotzky-Phillips-Sarnak] Can we approximate every graph this well?

Main Theorem for Graphs For every , there is a and s. t.

Main Theorem for Graphs For every , there is a and Within a factor of 2 of the Ramanujan bound s. t.
Matrix Sparsification

Matrix Sparsification

Matrix Sparsification

Main Theorem (Batson-S-Srivastava) For , there exist so that for and at most are non-zero
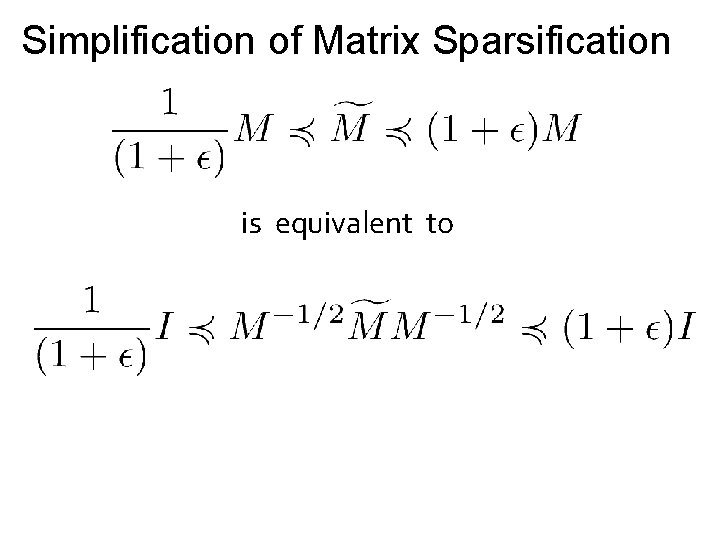
Simplification of Matrix Sparsification is equivalent to

Simplification of Matrix Sparsification Set “Decomposition of the identity”
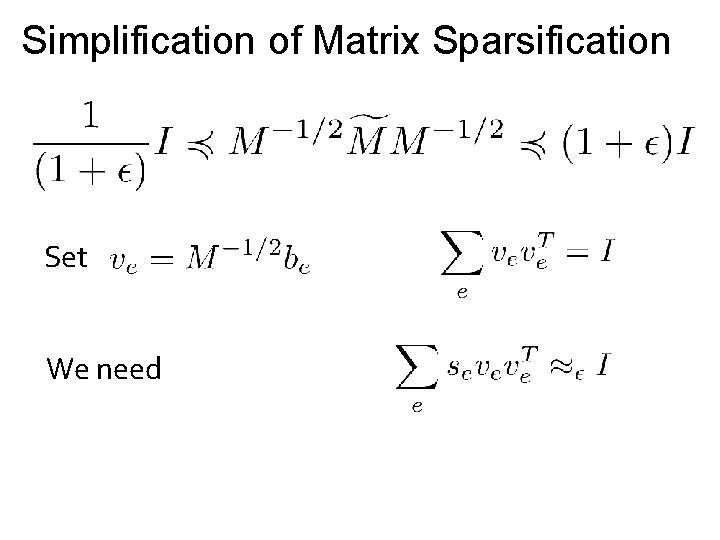
Simplification of Matrix Sparsification Set We need

Simplification of Matrix Sparsification Set We need Kadison-Singer all non-zero same

Simplification of Matrix Sparsification Set We need Plan: build set of vectors one-by-one

What happens when we add a vector?

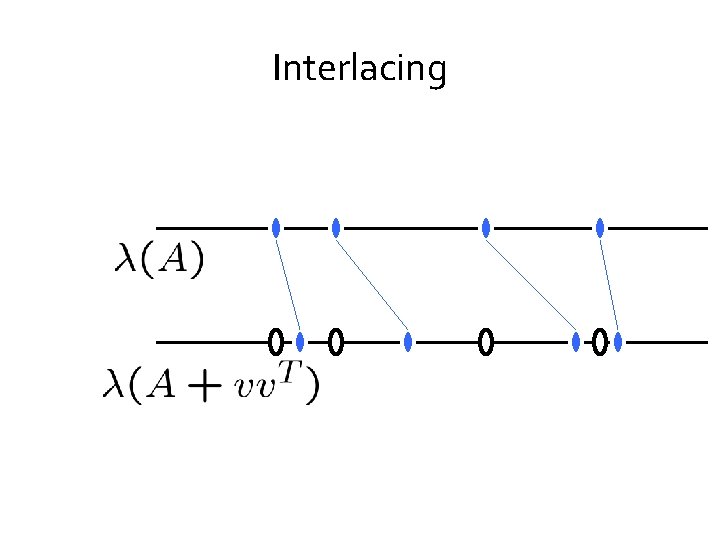
Interlacing
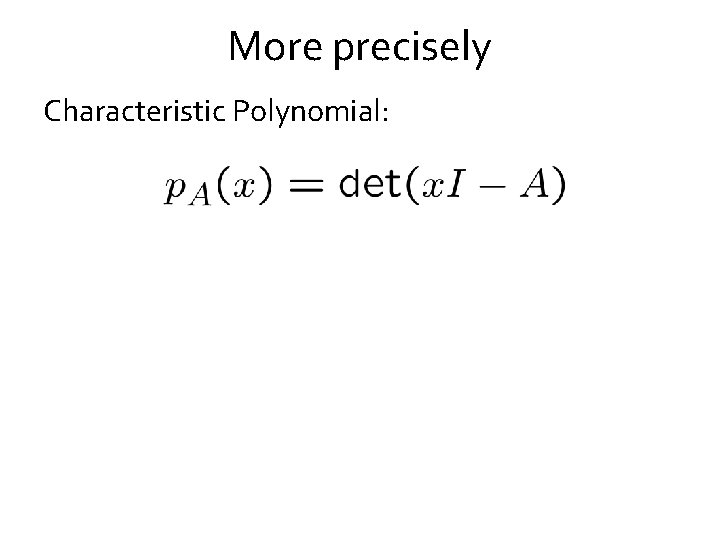
More precisely Characteristic Polynomial:

More precisely Characteristic Polynomial: Rank-one update: Where

Adding a random Because are decomposition of identity,
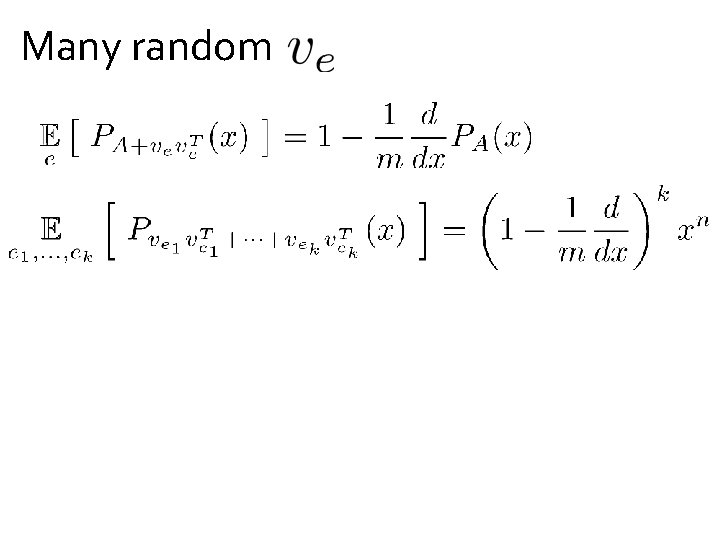
Many random

Many random Is an associated Laguerre polynomial! For , roots lie between and

The Expected Characteristic Polynomial For , roots lie between and

The Expected Characteristic Polynomial For , roots lie between and But, in general*, the roots of the individual polynomials have nothing to do with the roots of the expected polynomial.

The Expected Characteristic Polynomial For , roots lie between and But, in general*, the roots of the individual polynomials have nothing to do with the roots of the expected polynomial. * In the next two lectures, they do.

Matrix Sparsification Proof Sketch Have Want Will do with All eigenvalues between 1 and 13,

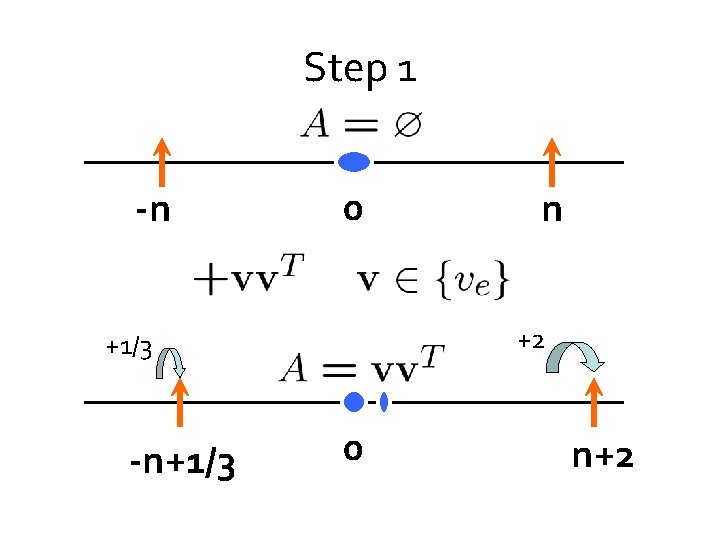
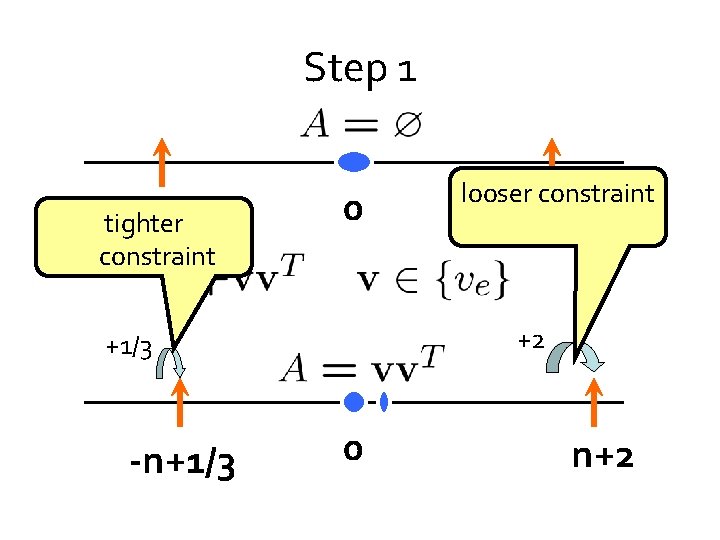
Broad outline: moving barriers -n 0 n

Step 1 -n 0 n

Step 1 -n 0 n

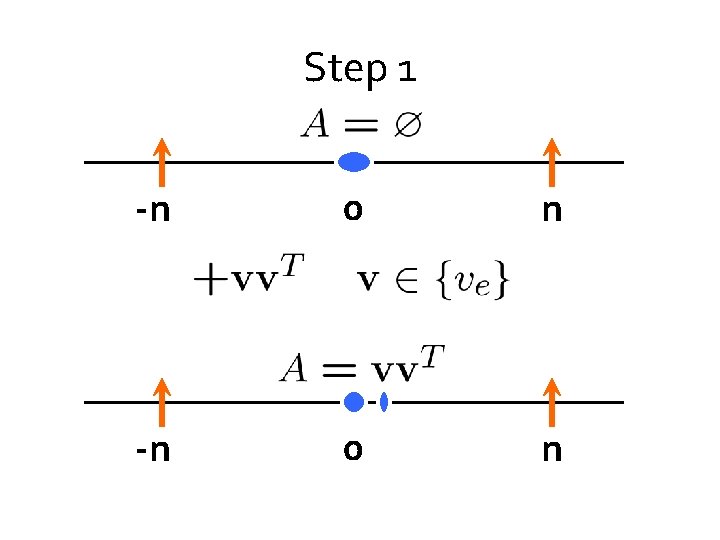
Step 1 -n 0 +2 +1/3 -n+1/3 n 0 n+2

Step 1 -n tighter constraint 0 n +2 +1/3 -n+1/3 looser constraint 0 n+2

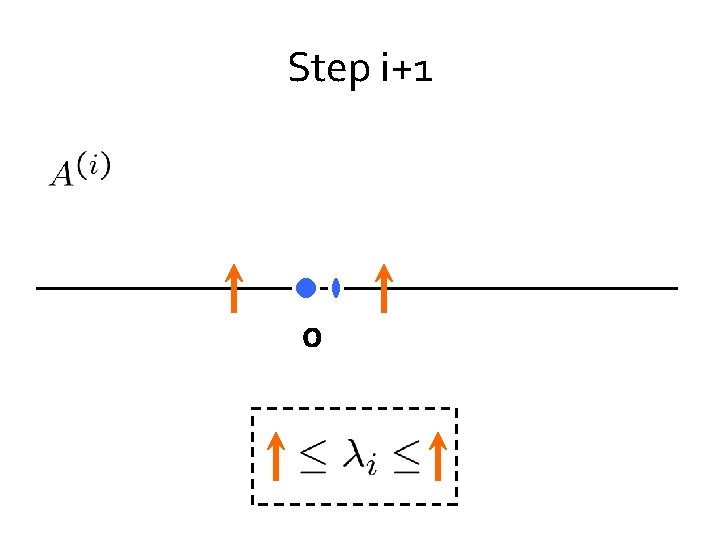
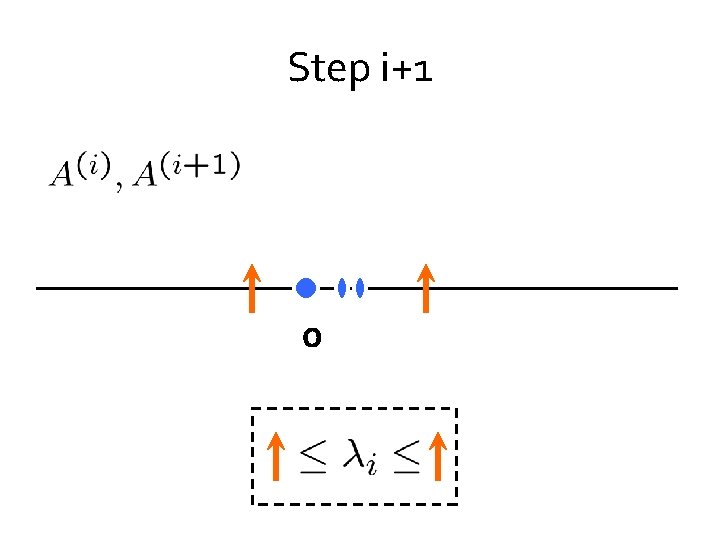
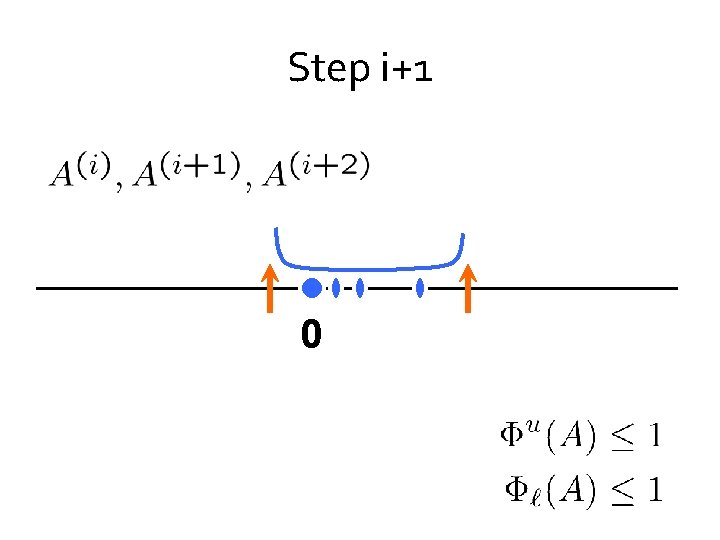
Step i+1 0

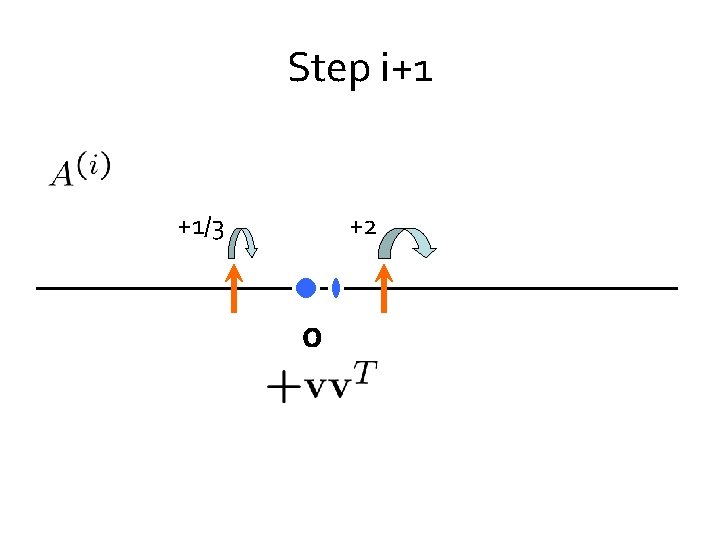
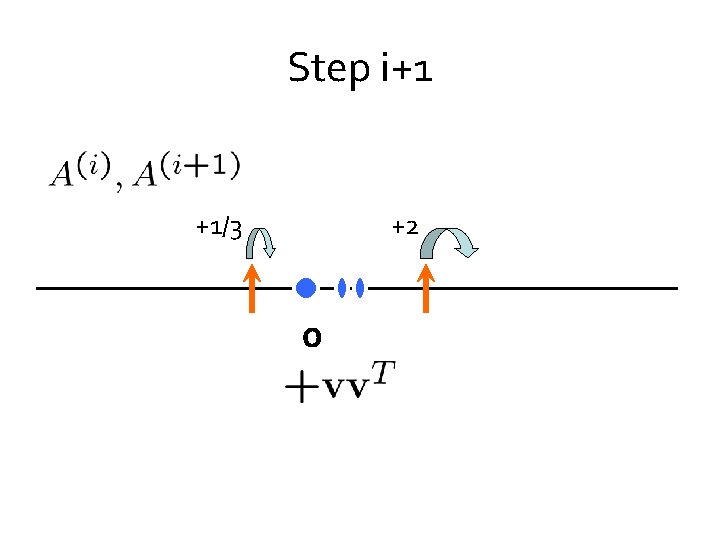
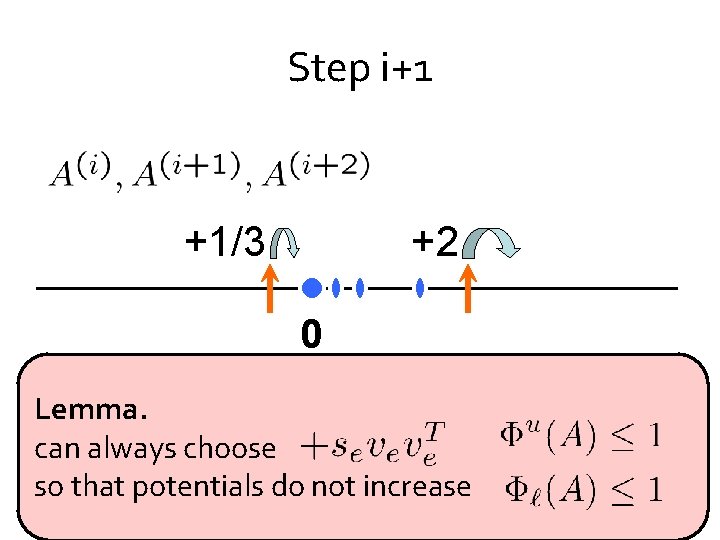
Step i+1 +1/3 +2 0

Step i+1 0

Step i+1 +1/3 +2 0

Step i+1 0

Step i+1 +1/3 +2 0

Step i+1 0

Step i+1 0

Step i+1 0

Step i+1 0

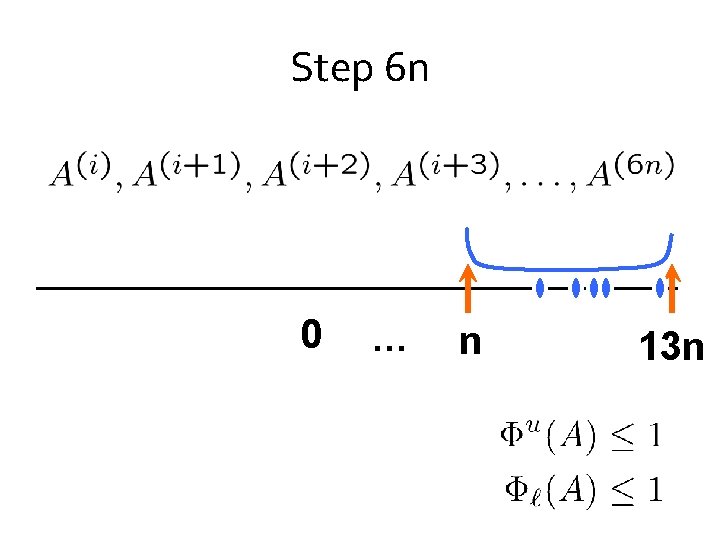
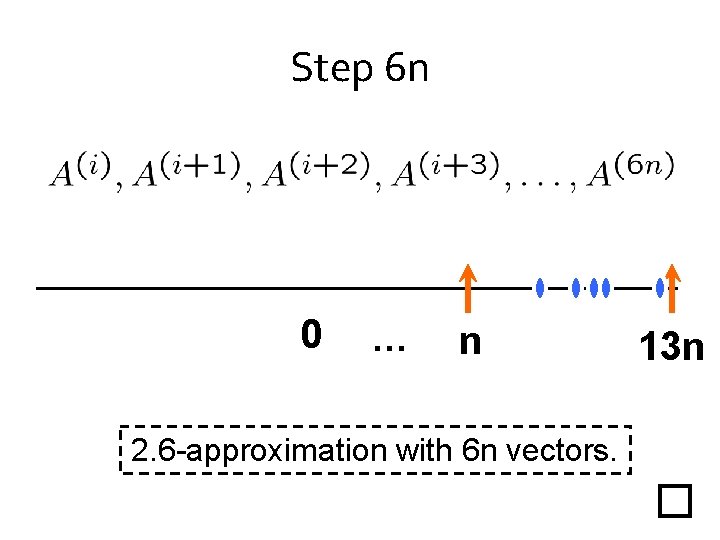
Step 6 n 0 … n 13 n

Step 6 n 0 … n 2. 6 -approximation with 6 n vectors. 13 n

Problem need to show that an appropriate always exists.

Problem need to show that an appropriate always exists. Is not strong enough for induction

Problems If many small eigenvalues, can only move one Bunched large eigenvalues repel the highest one

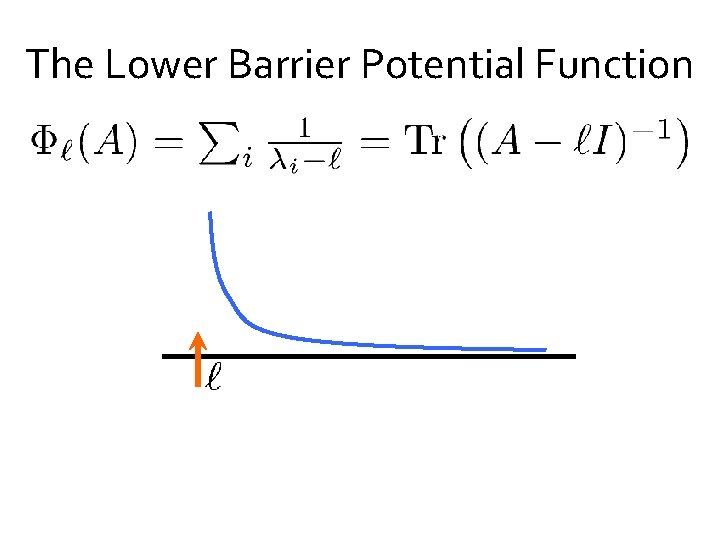
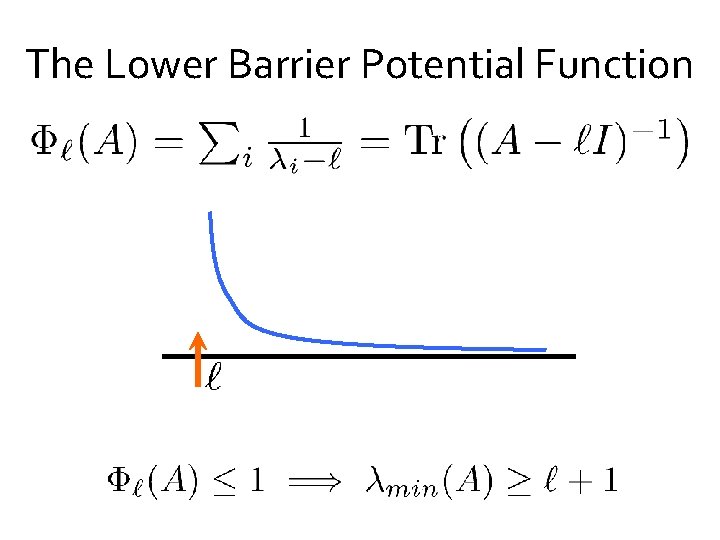
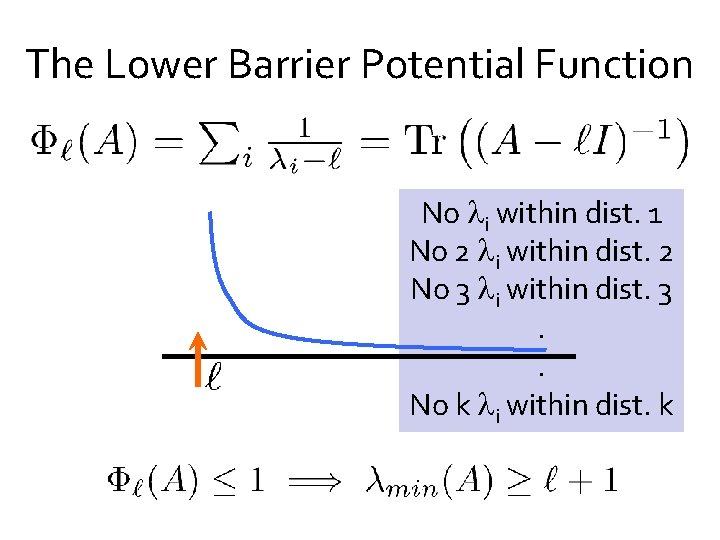
The Lower Barrier Potential Function

The Lower Barrier Potential Function

The Lower Barrier Potential Function No i within dist. 1 No 2 i within dist. 2 No 3 i within dist. 3. . No k i within dist. k

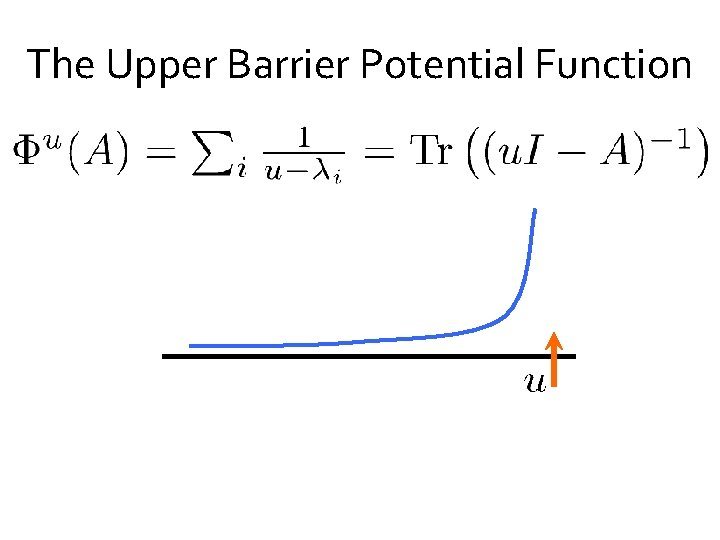
The Upper Barrier Potential Function

The Beginning -n 0 n

The Beginning -n 0 n

Step i+1 0

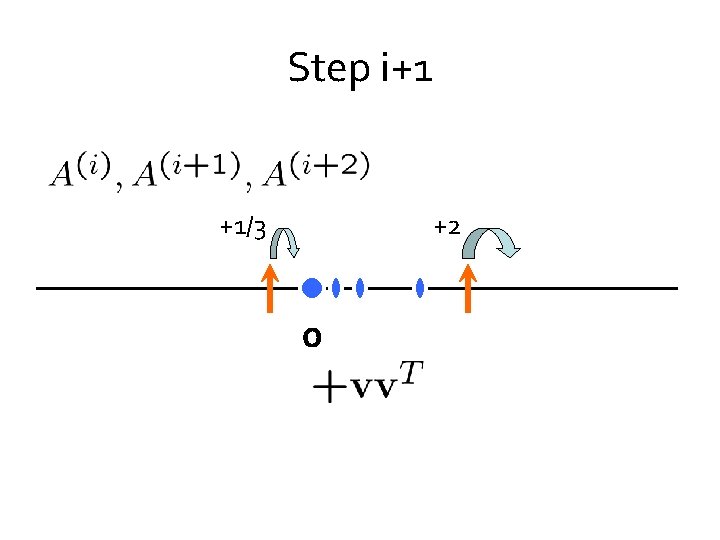
Step i+1 +1/3 +2 0 Lemma. can always choose so that potentials do not increase

Step i+1 0

Step i+1 0

Step i+1 0

Step i+1 0

Step 6 n 0 … n 13 n

Step 6 n 0 … n 2. 6 -approximation with 6 n vectors. 13 n

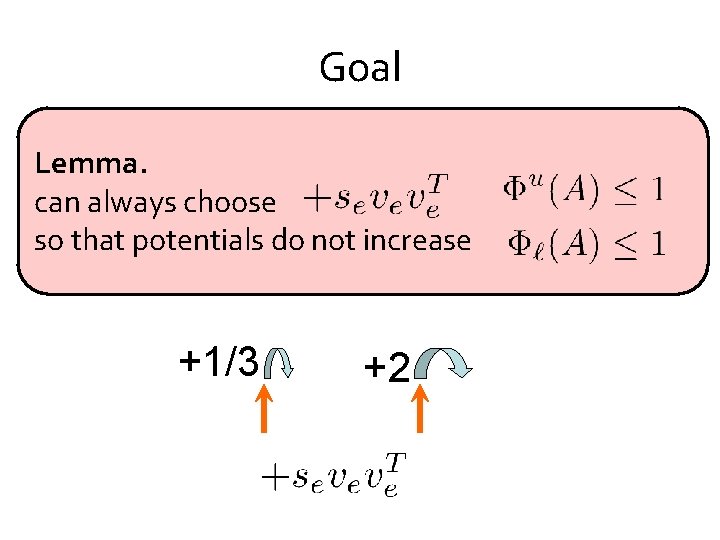
Goal Lemma. can always choose so that potentials do not increase +1/3 +2

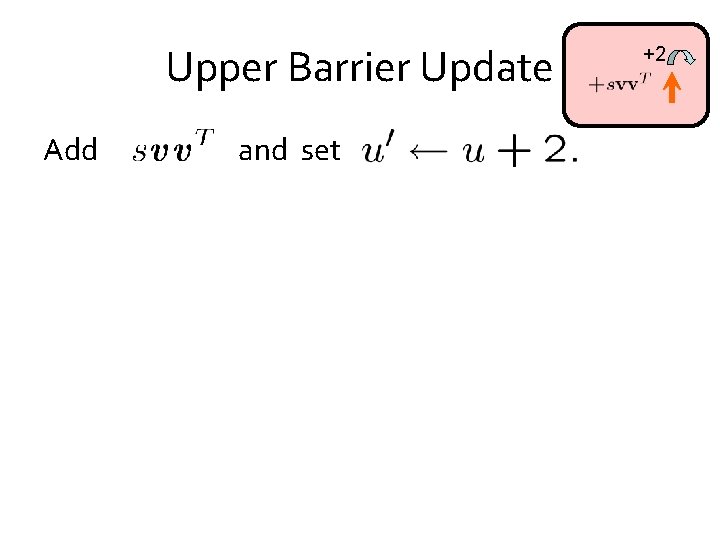
Upper Barrier Update Add and set +2

Upper Barrier Update Add and set +2

Upper Barrier Update Add and set By Sherman-Morrison Formula +2

Upper Barrier Update Add Need and set +2
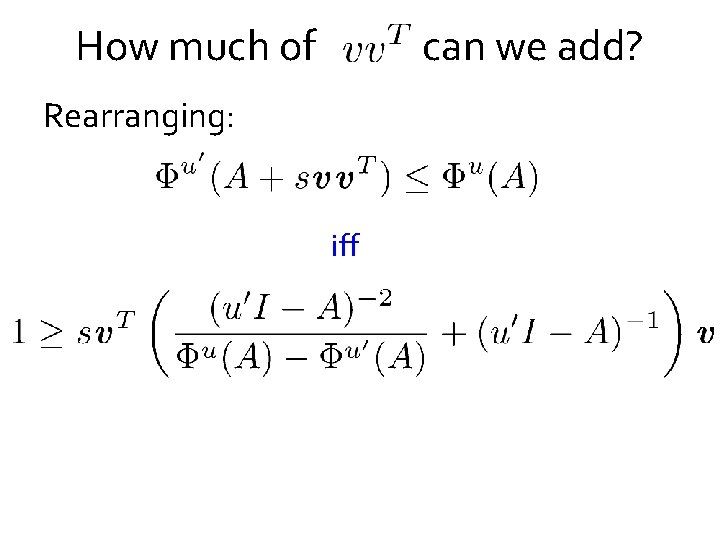
How much of can we add? Rearranging: iff
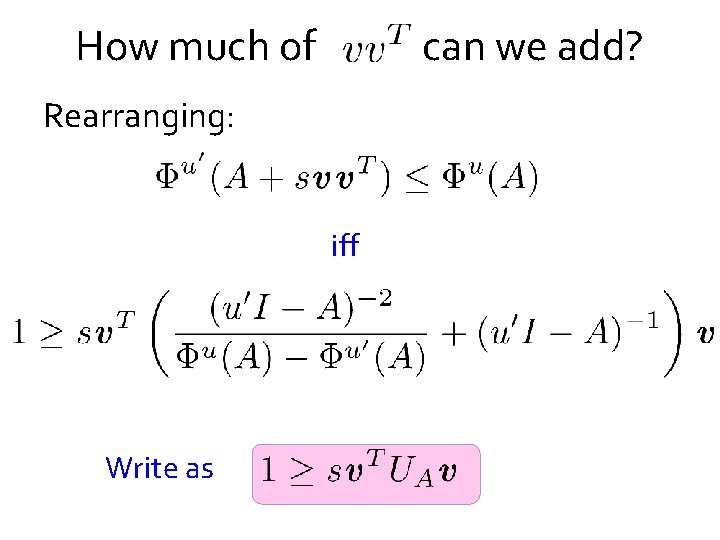
How much of can we add? Rearranging: iff Write as

Lower Barrier Similarly: iff Write as

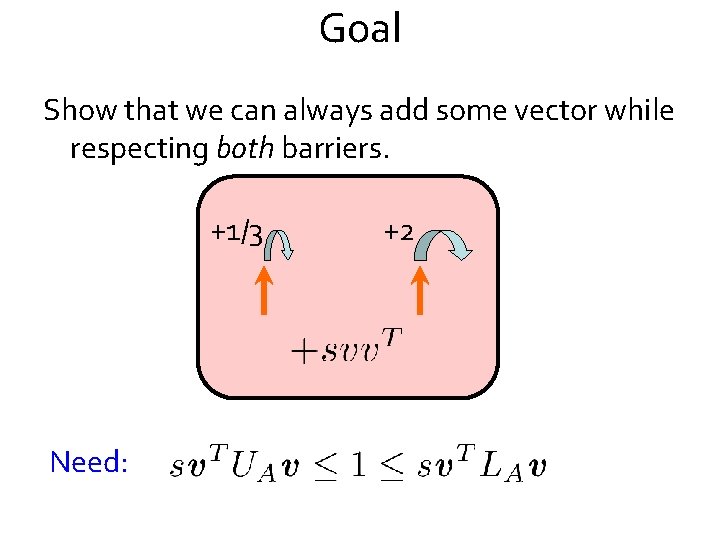
Goal Show that we can always add some vector while respecting both barriers. +1/3 Need: +2

Two expectations Need: Can show:

Two expectations Need: Can show: So: And, exists

Two expectations Need: Can show: So: And, exists And that puts between them

Two expectations Need: Can show: So: And, exists And that puts between them

Bounding expectations

Bounding expectations As barrier function is monotone decreasing

Bounding expectations Numerator is derivative of barrier function. As barrier function is convex,

Bounding expectations “Similarly”,

Step i+1 +1/3 +2 0 Lemma. can always choose so that potentials do not increase

Twice-Ramanujan Sparsifiers Fixing steps and tightening parameters gives ratio Less than twice as many edges as used by Ramanujan Expander of same quality

Open Questions Ramanujan sparsifiers? Properties of vectors from graphs? Faster algorithm union of random Hamiltonian cycles?

What’s next Exploit expected characteristic polynomials Kadison-Singer Ramanujan Graphs of every degree