Graphs Vectors and Matrices Daniel A Spielman Yale






















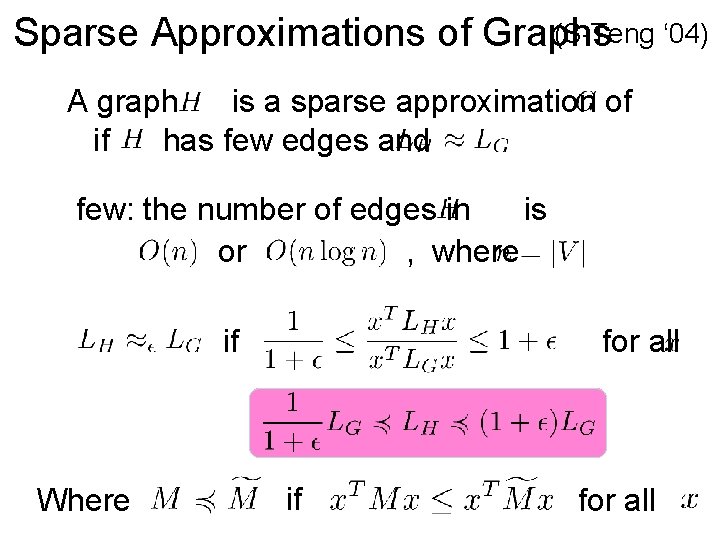







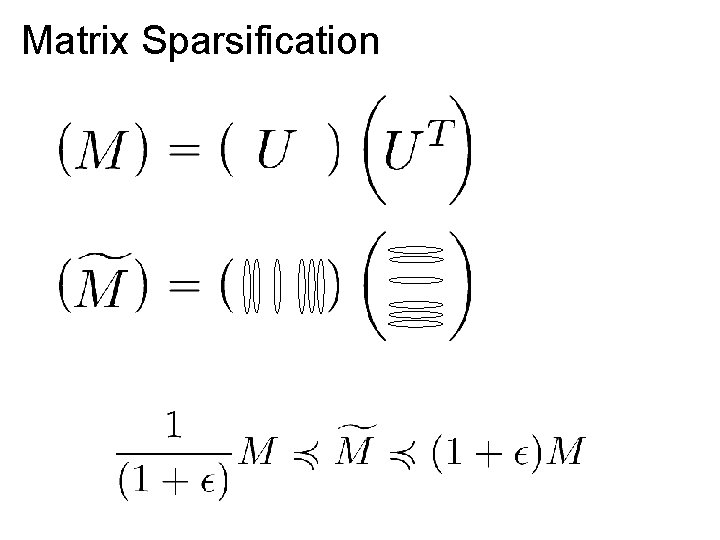



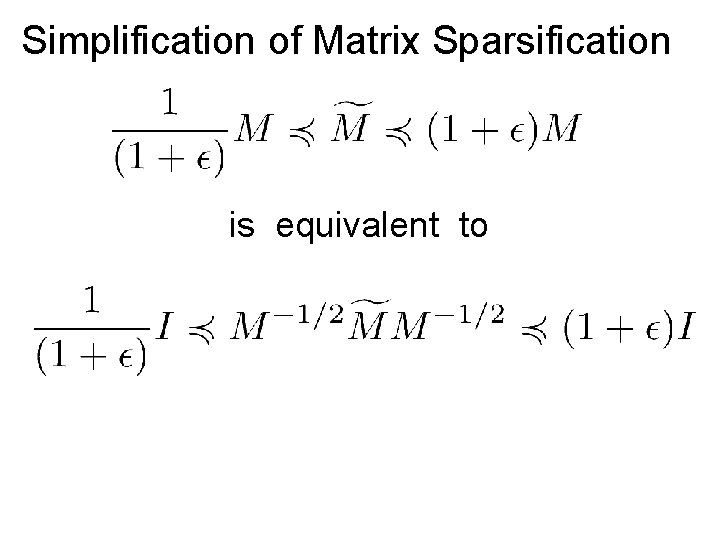
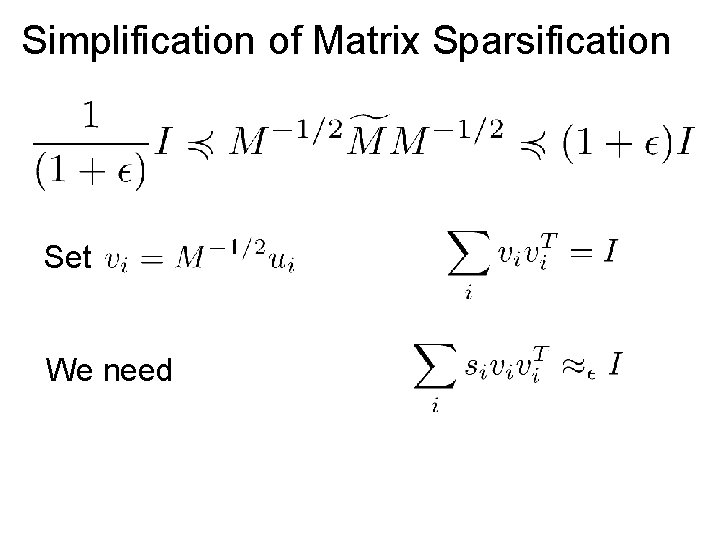












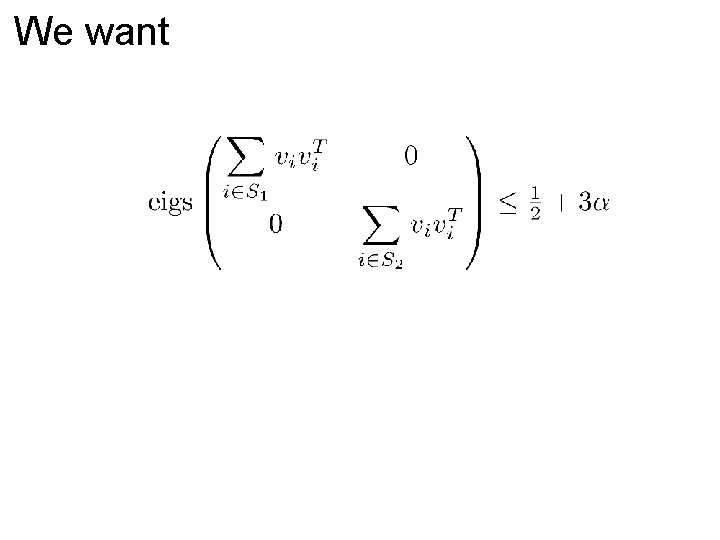
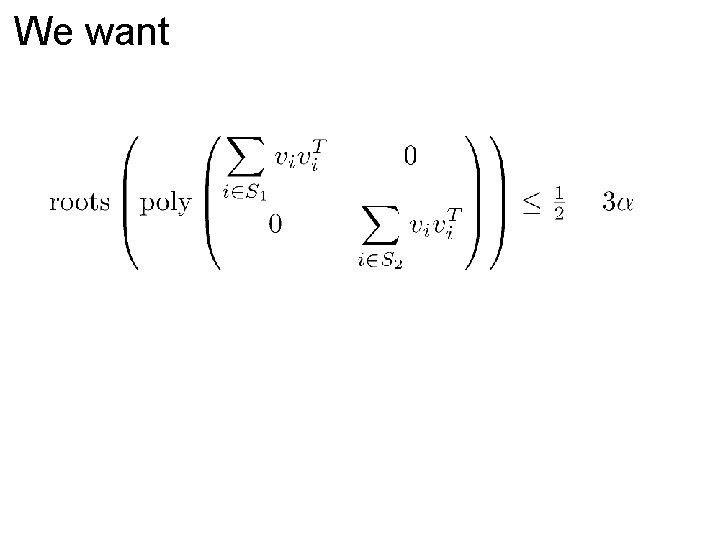





- Slides: 105

Graphs, Vectors, and Matrices Daniel A. Spielman Yale University AMS Josiah Willard Gibbs Lecture January 6, 2016

From Applied to Pure Mathematics Algebraic and Spectral Graph Theory Sparsification: approximating graphs by graphs with fewer edg The Kadison-Singer problem

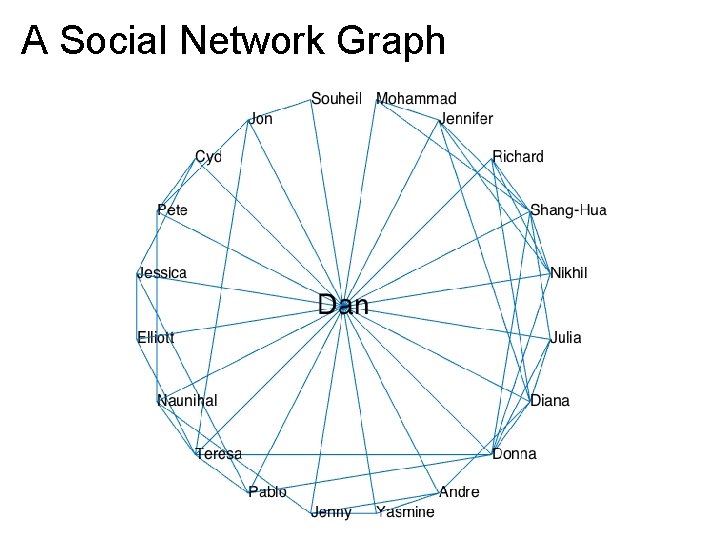
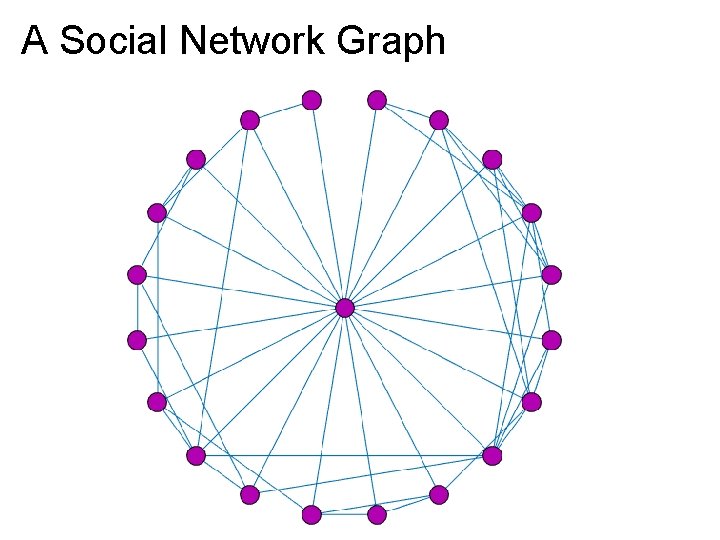
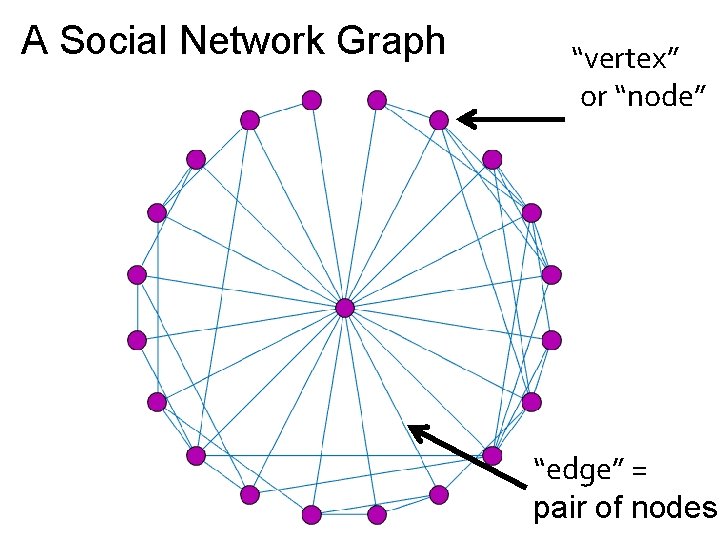
A Social Network Graph

A Social Network Graph

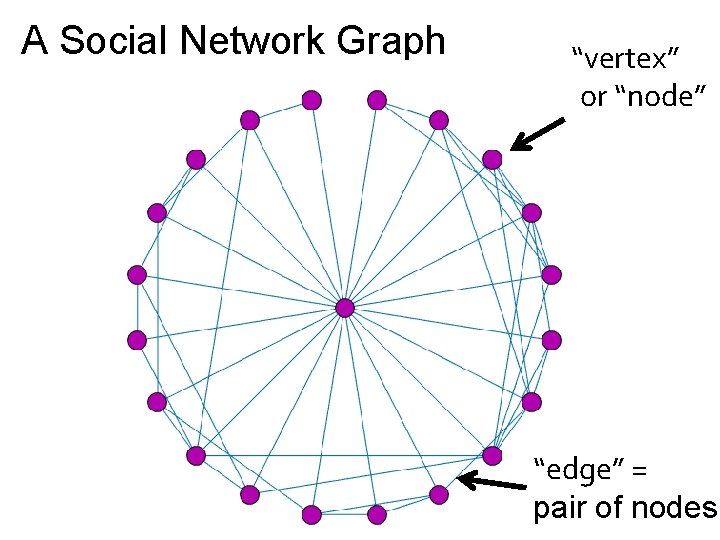
A Social Network Graph “vertex” or “node” “edge” = pair of nodes

A Social Network Graph “vertex” or “node” “edge” = pair of nodes

A Big Social Network Graph

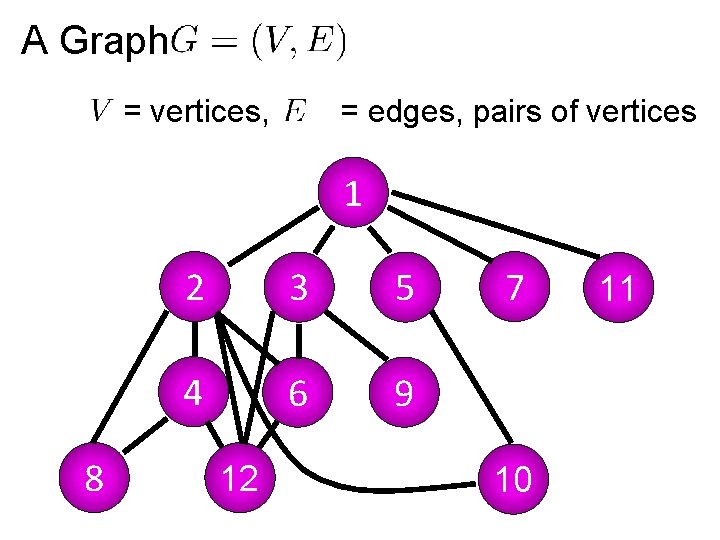
A Graph = vertices, = edges, pairs of vertices 1 8 2 3 5 4 6 9 12 7 10 11

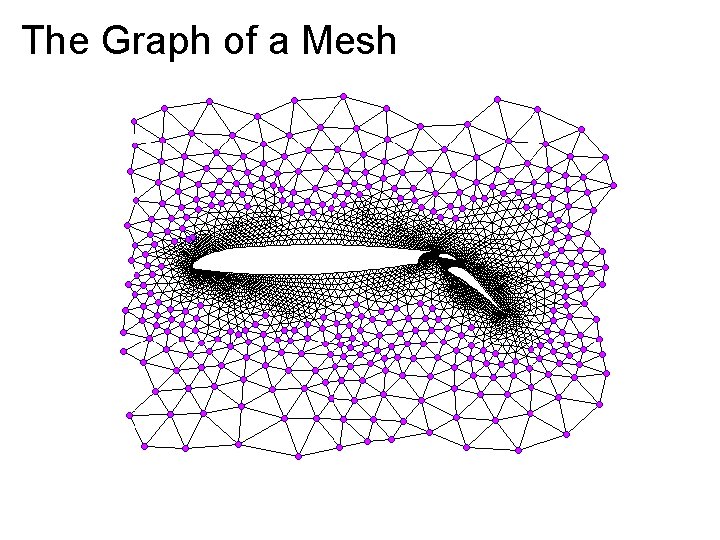
The Graph of a Mesh

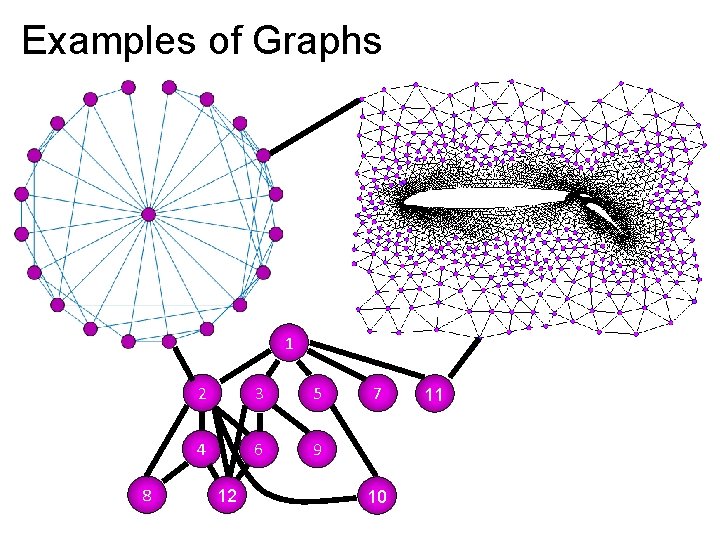
Examples of Graphs 1 8 2 3 5 4 6 9 12 7 10 11

Examples of Graphs 1 8 2 3 5 4 6 9 12 7 10 11

How to understand large-scale structure Draw the graph Identify communities and hierarchical structure Use physical metaphors Edges as resistors or rubber bands Examine processes Diffusion of gas / Random Walks

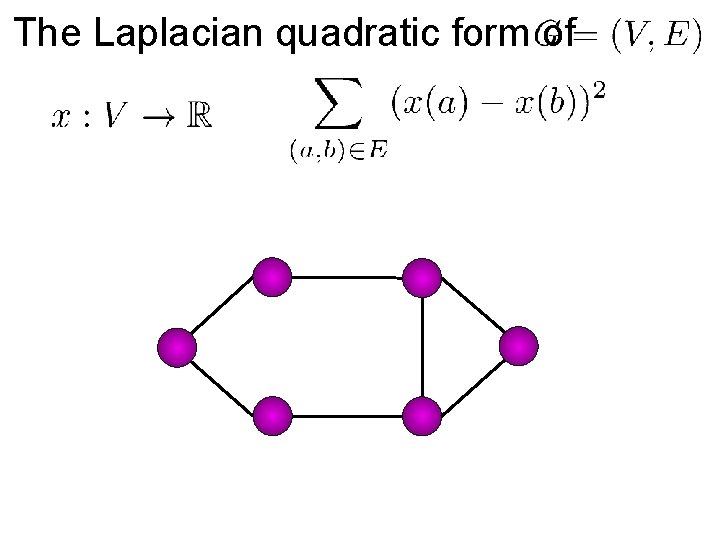
The Laplacian quadratic form of

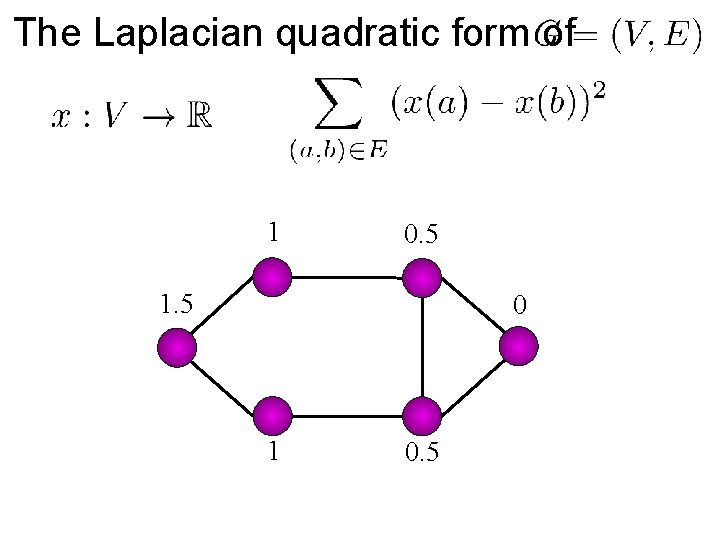
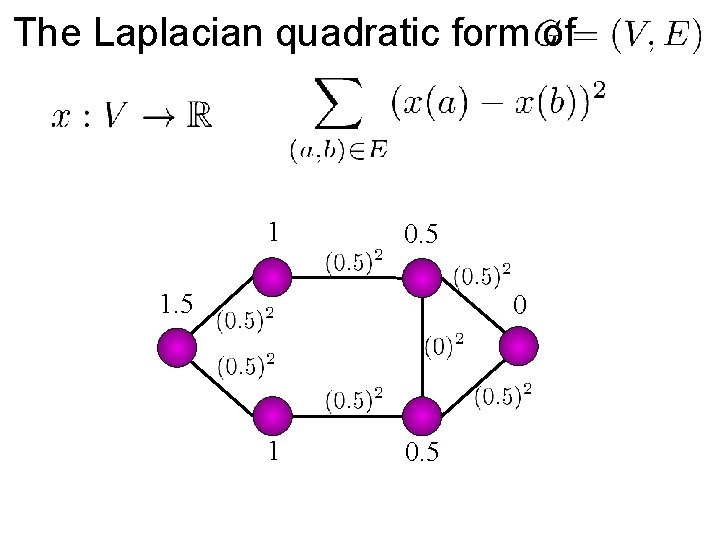
The Laplacian quadratic form of 1 0. 5 1. 5 0 1 0. 5

The Laplacian quadratic form of 1 0. 5 1. 5 0 1 0. 5

The Laplacian matrix of

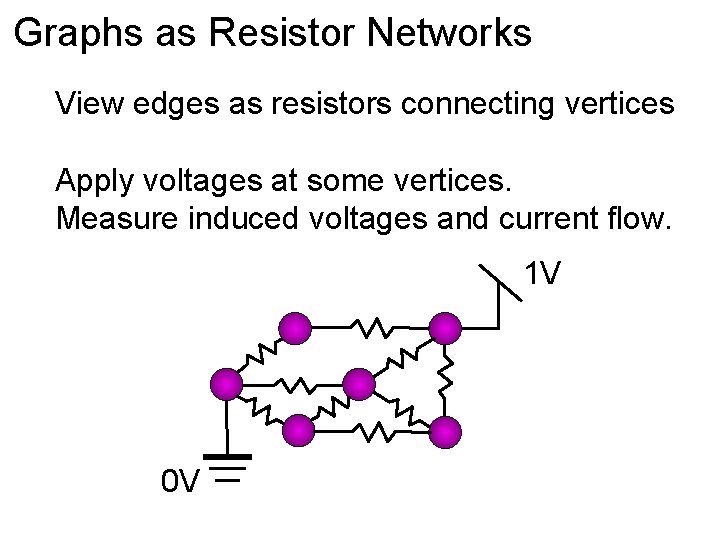
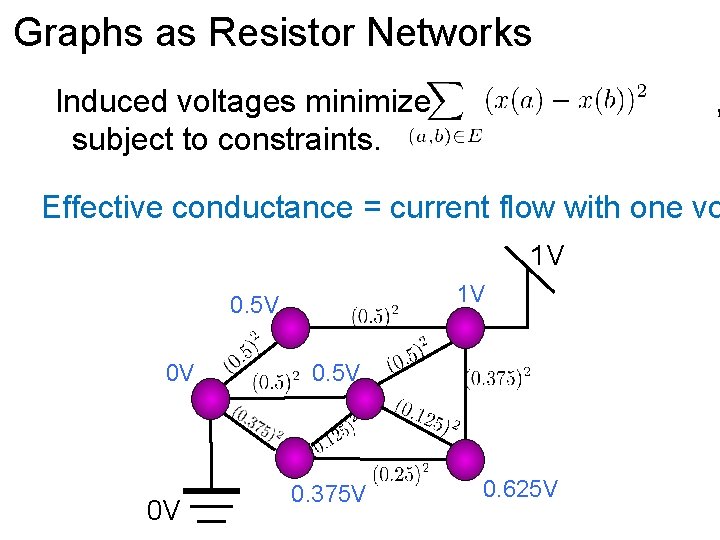
Graphs as Resistor Networks View edges as resistors connecting vertices Apply voltages at some vertices. Measure induced voltages and current flow. 1 V 0 V

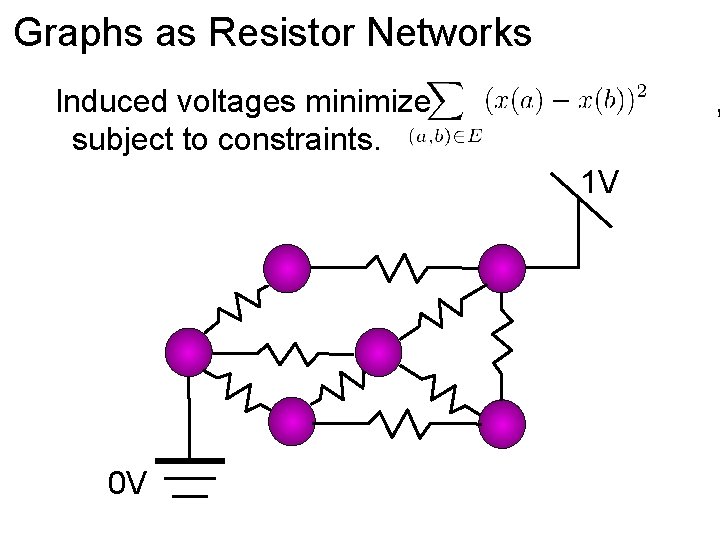
Graphs as Resistor Networks Induced voltages minimize subject to constraints. , 1 V 0 V

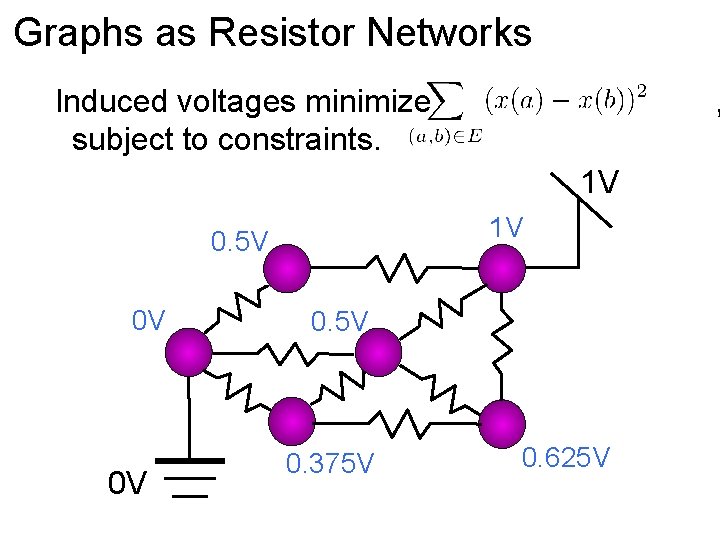
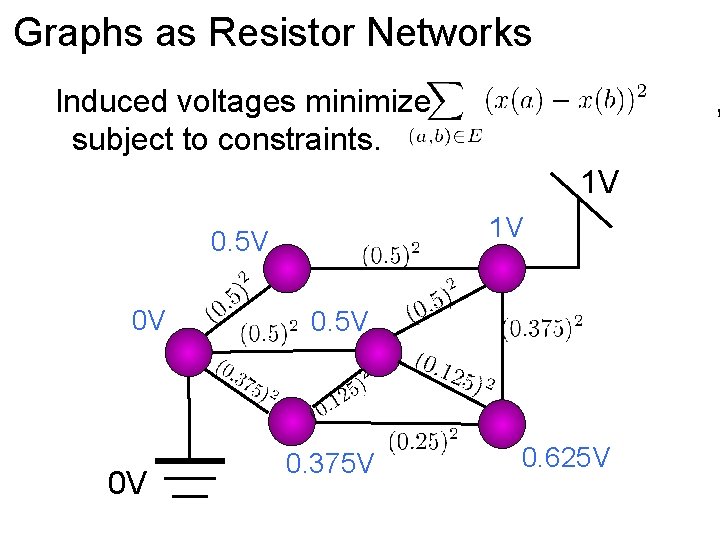
Graphs as Resistor Networks Induced voltages minimize subject to constraints. , 1 V 1 V 0. 5 V 0 V 0 V 0. 5 V 0. 375 V 0. 625 V

Graphs as Resistor Networks Induced voltages minimize subject to constraints. , 1 V 1 V 0. 5 V 0 V 0 V 0. 5 V 0. 375 V 0. 625 V

Graphs as Resistor Networks Induced voltages minimize subject to constraints. , Effective conductance = current flow with one vo 1 V 1 V 0. 5 V 0 V 0 V 0. 5 V 0. 375 V 0. 625 V

Weighted Graphs Edge assigned a non-negative real weigh measuring strength of connection 1/resistance

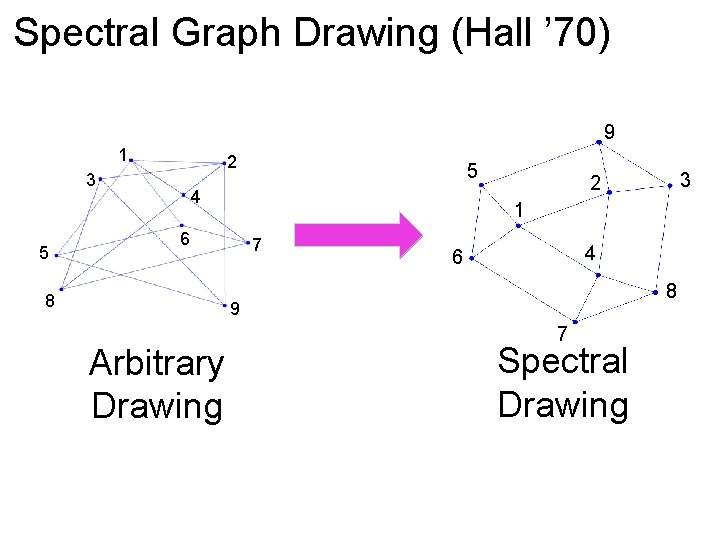
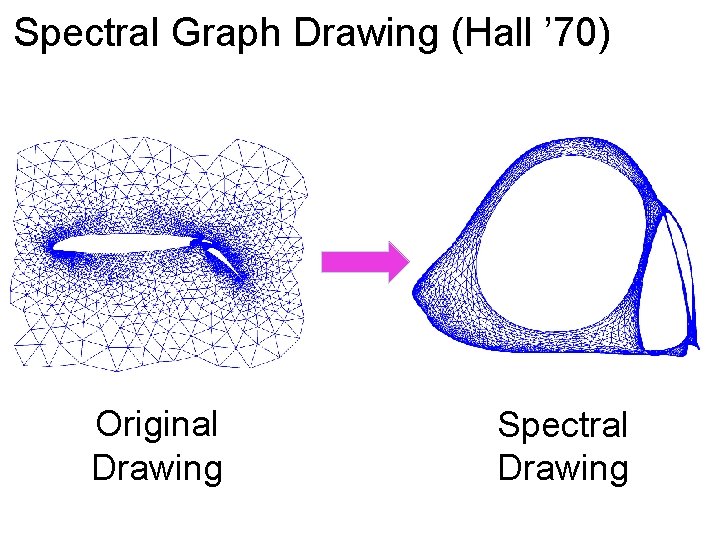
Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Edges are drawn as curves for visibility.

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize to fix scale, require

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize to fix scale, require

Courant-Fischer Theorem Where is the smallest eigenvalue of and is the corresponding eigenvector.

Courant-Fischer Theorem Where is the smallest eigenvalue of and is the corresponding eigenvector. For and is a constant vector

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize Such that and

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize Such that and Courant-Fischer Theorem: solution is , the eigenvector of the second-smallest eigenvalue ,

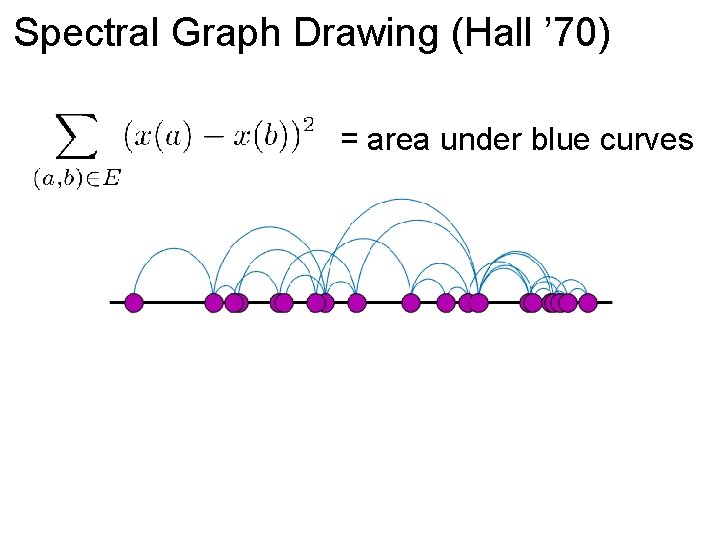
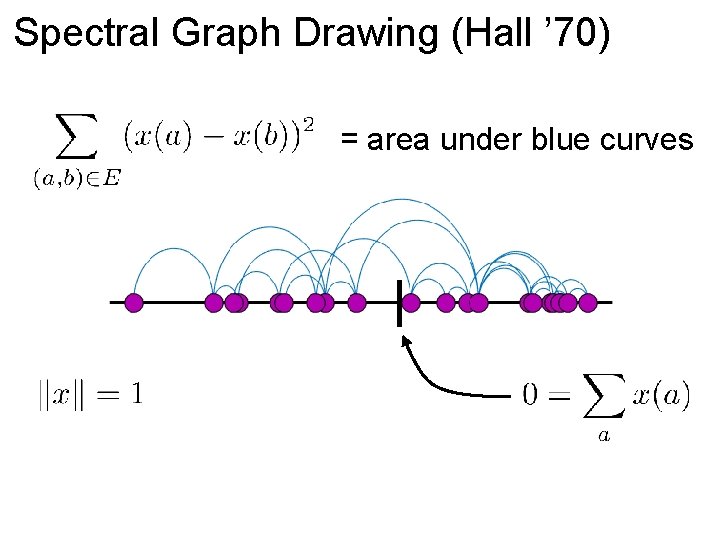
Spectral Graph Drawing (Hall ’ 70) = area under blue curves

Spectral Graph Drawing (Hall ’ 70) = area under blue curves

Space the points evenly

And, move them to the circle

Finish by putting me back in the center

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize Such that and

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize Such that and

Spectral Graph Drawing (Hall ’ 70) Want to map with most edges short Minimize Such that and and , to prevent

Spectral Graph Drawing (Hall ’ 70) Minimize Such that and Courant-Fischer Theorem: solution is , up to rotation

Spectral Graph Drawing (Hall ’ 70) 9 1 2 3 5 5 4 1 6 8 7 4 6 8 9 Arbitrary Drawing 3 2 7 Spectral Drawing

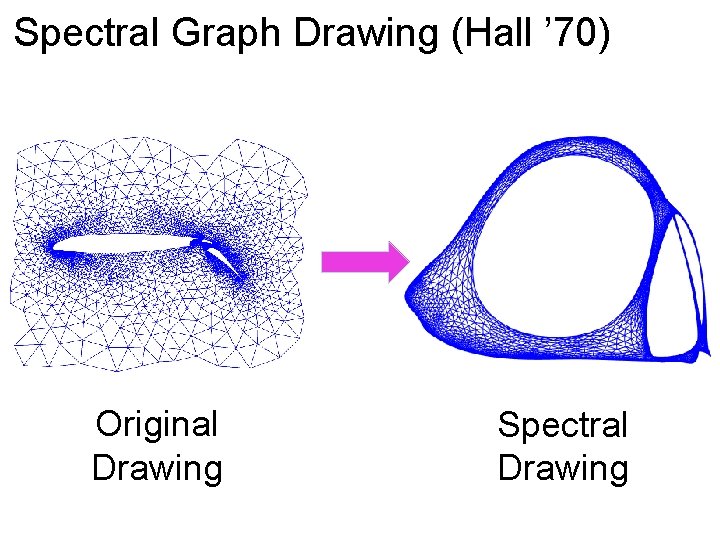
Spectral Graph Drawing (Hall ’ 70) Original Drawing Spectral Drawing

Spectral Graph Drawing (Hall ’ 70) Original Drawing Spectral Drawing

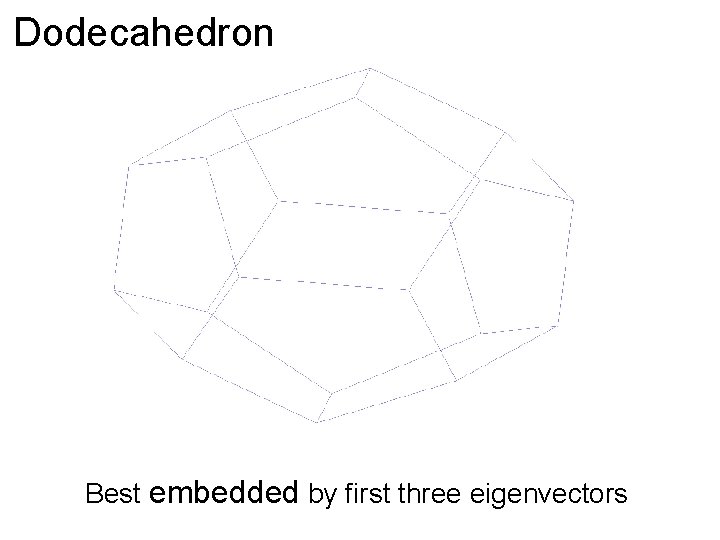
Dodecahedron Best embedded by first three eigenvectors

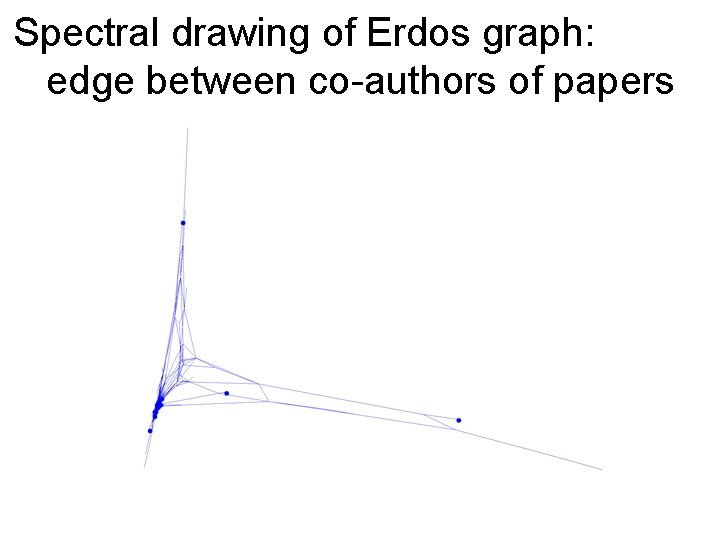
Spectral drawing of Erdos graph: edge between co-authors of papers

When there is a “nice” drawing: Most edges are short Vertices are spread out and don’t clump too mu is close to 0 When is big, say there is no nice picture of the graph

Expanders: when is big Formally: infinite families of graphs of constant degree d and large Examples: random d-regular graphs Ramanujan graphs Have no communities or clusters. Incredibly useful in Computer Science: Act like random graphs (pseudo-random) Used in many important theorems and algorit

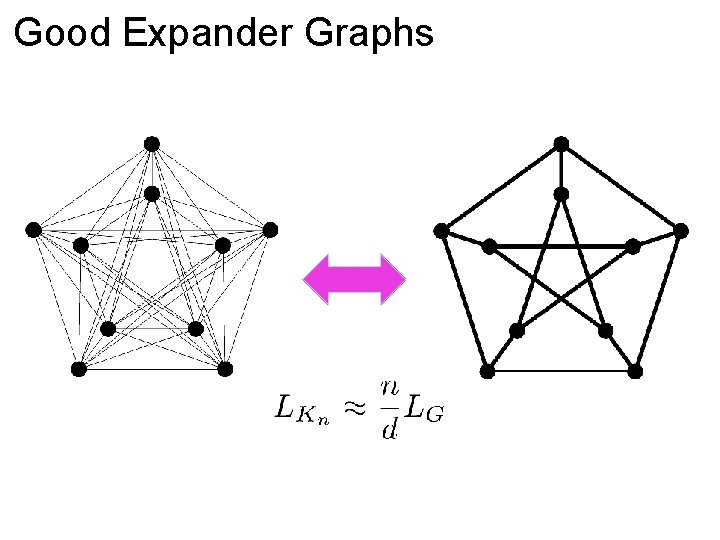
Good Expander Graphs -regular graphs with Courant-Fischer: for all

Good Expander Graphs -regular graphs with Courant-Fischer: for all For , the complete graph on , so for vertices

Good Expander Graphs

(S-Teng ‘ 04) Sparse Approximations of Graphs A graph is a sparse approximation of if has few edges and few: the number of edges in is or , where if for all

(S-Teng ‘ 04) Sparse Approximations of Graphs A graph is a sparse approximation of if has few edges and few: the number of edges in is or , where if Where for all if for all
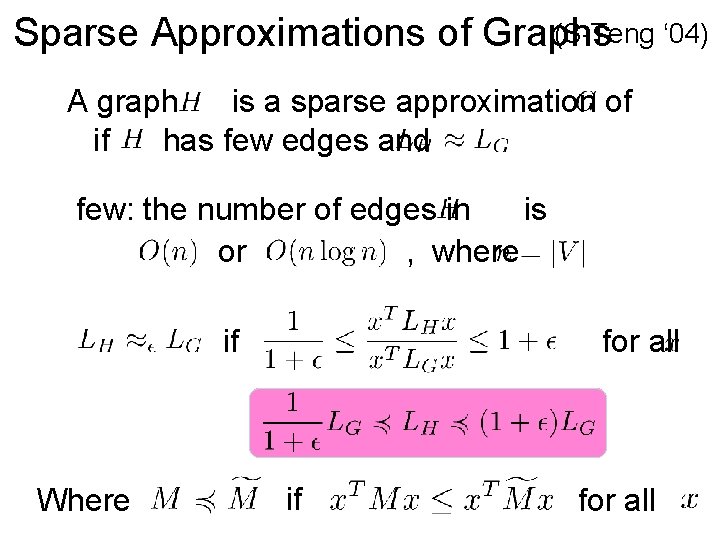
(S-Teng ‘ 04) Sparse Approximations of Graphs A graph is a sparse approximation of if has few edges and few: the number of edges in is or , where if Where for all if for all

(S-Teng ‘ 04) Sparse Approximations of Graphs The number of edges in is or , where Where if for all

Why we sparsify graphs To save memory when storing graphs. To speed up algorithms: flow problems in graphs (Benczur-Karger ‘ 96) linear equations in Laplacians (S-Teng ‘ 04)

Graph Sparsification Theorems For every , there is a and (Batson-S-Srivastava ‘ 0

Graph Sparsification Theorems For every , there is a and (Batson-S-Srivastava ‘ 0 By careful random sampling, can quickly get (S-Srivastava ‘ 08)

Laplacian Matrices

Laplacian Matrices

Laplacian Matrices
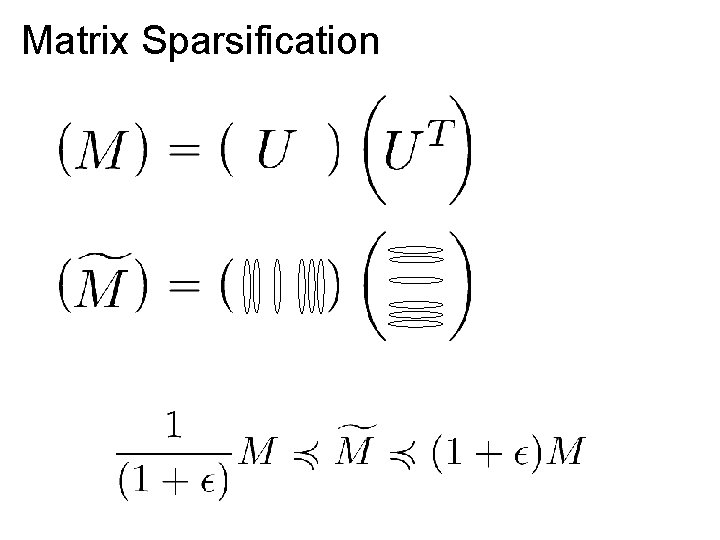
Matrix Sparsification

Matrix Sparsification subset of vectors, scaled up

Matrix Sparsification subset of vectors, scaled up

Matrix Sparsification
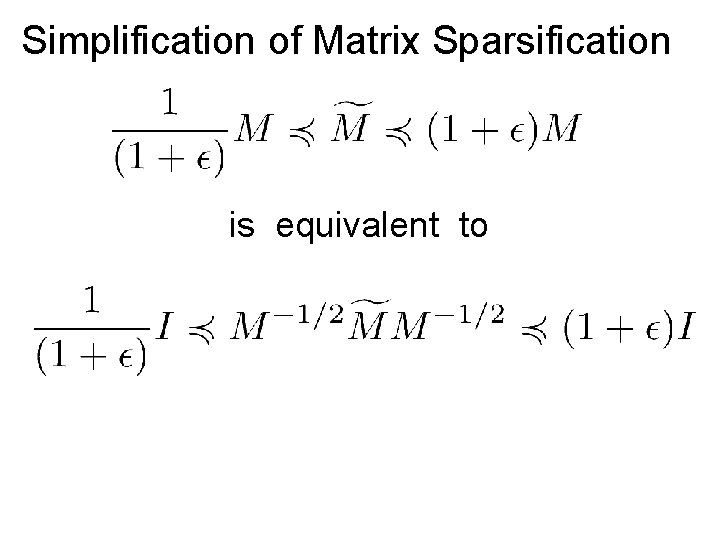
Simplification of Matrix Sparsification is equivalent to
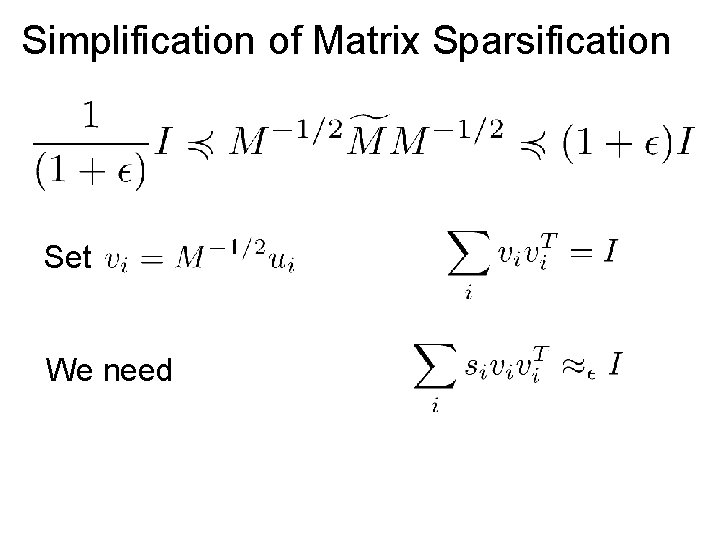
Simplification of Matrix Sparsification Set We need

Simplification of Matrix Sparsification Set “Decomposition of the identity” “Parseval frame” “Isotropic Position”

Matrix Sparsification by Sampling (Rudelson ‘ 99, Ahlswede-Winter ‘ 02, Tropp ’ 11) For Choose If choose with probability , set

Matrix Sparsification by Sampling (Rudelson ‘ 99, Ahlswede-Winter ‘ 02, Tropp ’ 11) For Choose If choose with probability , set (effective conductance

Matrix Sparsification by Sampling (Rudelson ‘ 99, Ahlswede-Winter ‘ 02, Tropp ’ 11) For Choose If choose with probability , set

Matrix Sparsification by Sampling (Rudelson ‘ 99, Ahlswede-Winter ‘ 02, Tropp ’ 11) For Choose If choose with probability , set With high probability, choose vectors an d

Optimal (? ) Matrix Sparsification (Batson-S-Srivastava ‘ 09 For with Can choose vectors and nonzero values for the so that

Optimal (? ) Matrix Sparsification (Batson-S-Srivastava ‘ 09 For with Can choose vectors and nonzero values for the so that What are the !?

Optimal (? ) Matrix Sparsification (Batson-S-Srivastava ‘ 09 For with Can choose vectors and nonzero values for the so that !?

The Kadison-Singer Problem ‘ 59 Equivalent to: Anderson’s Paving Conjectures (‘ 79, ‘ 81) Bourgain-Tzafriri Conjecture (‘ 91) Feichtinger Conjecture (‘ 05) Many others Implied by: Weaver’s KS 2 conjecture (‘ 04)

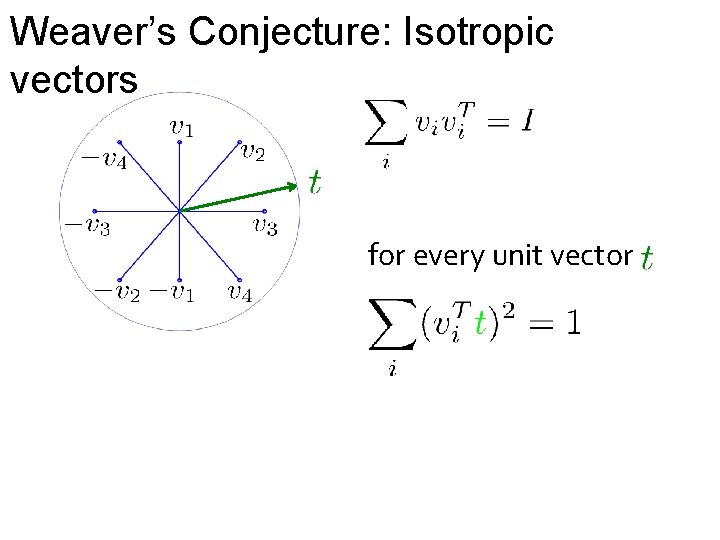
Weaver’s Conjecture: Isotropic vectors for every unit vector

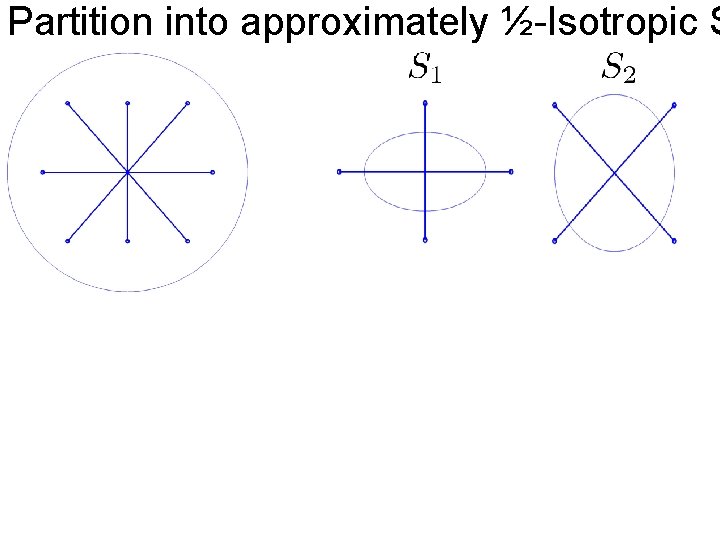
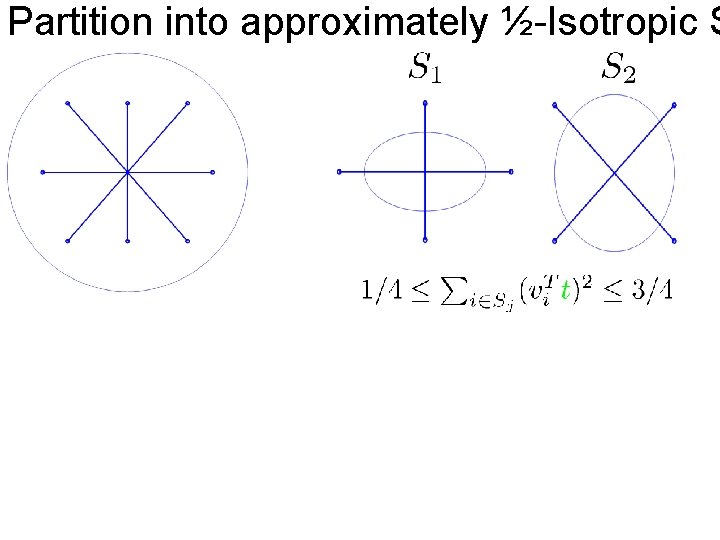
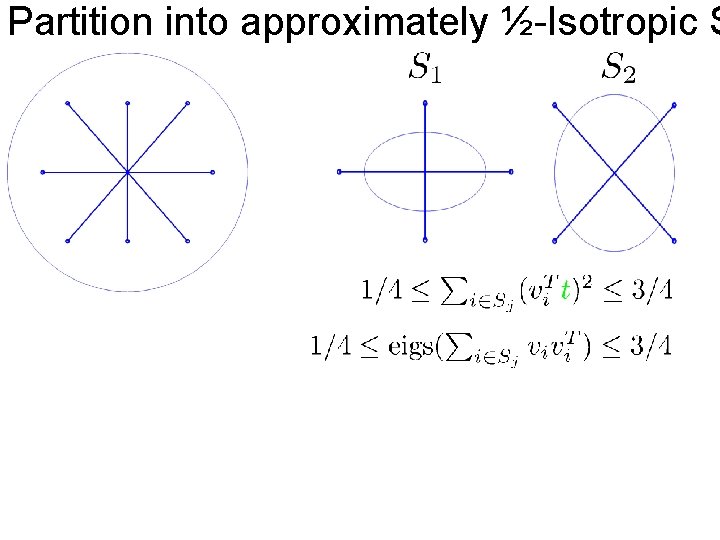
Partition into approximately ½-Isotropic S

Partition into approximately ½-Isotropic S

Partition into approximately ½-Isotropic S

Partition into approximately ½-Isotropic S because

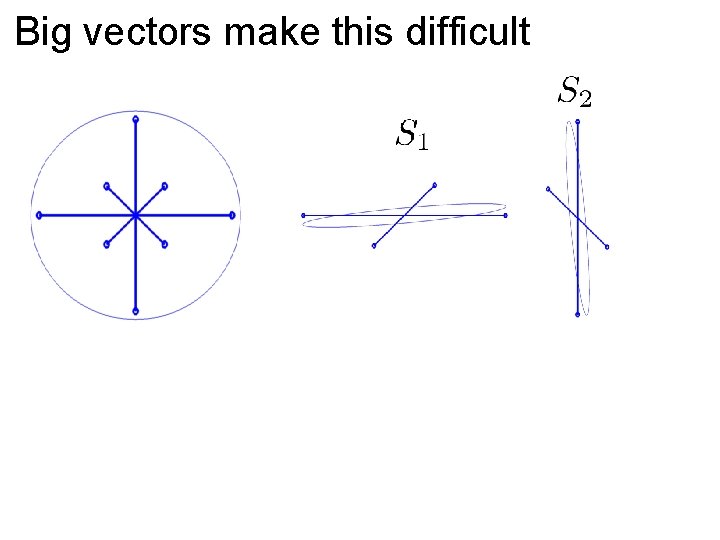
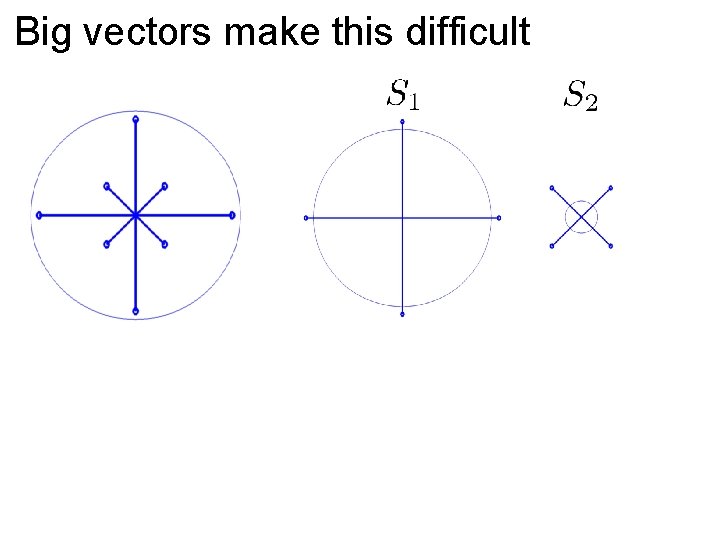
Big vectors make this difficult

Big vectors make this difficult

Weaver’s Conjecture KS 2 There exist positive constants if all and so that and then exists a partition into S 1 and S 2 with

Theorem (Marcus-S-Srivastava ‘ 15) For all if all and then exists a partition into S 1 and S 2 with
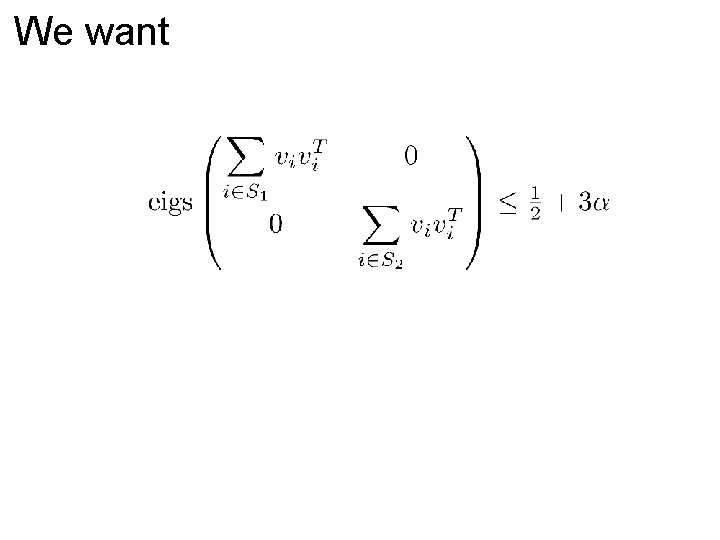
We want
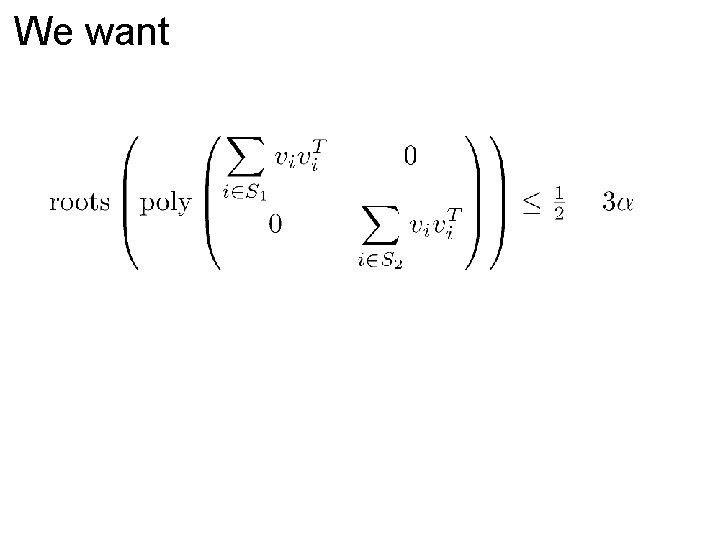
We want

We want Consider expected polynomial of a random partiti

Proof Outline 1. Prove expected characteristic polynomial has real roots 2. Prove its largest root is at most 3. Prove is an interlacing family, so exists a partition whose polynomial has largest root at most

Interlacing Polynomial interlaces if Example:

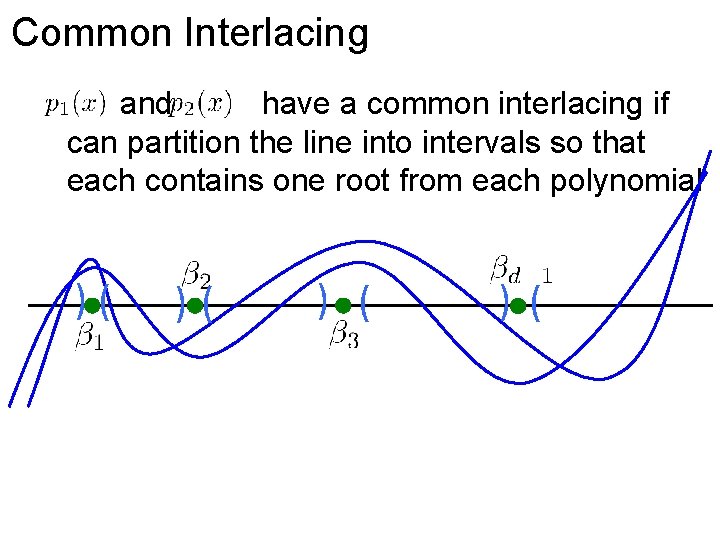
Common Interlacing and have a common interlacing if can partition the line into intervals so that each contains one root from each polynomial )( )( ) ( )(

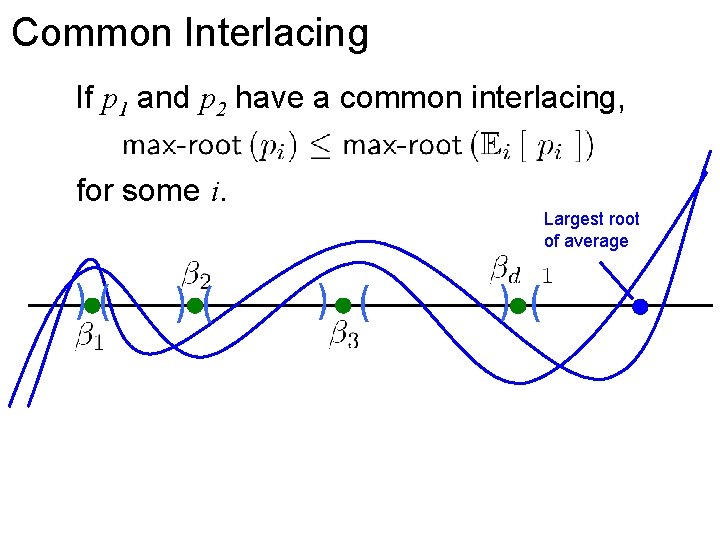
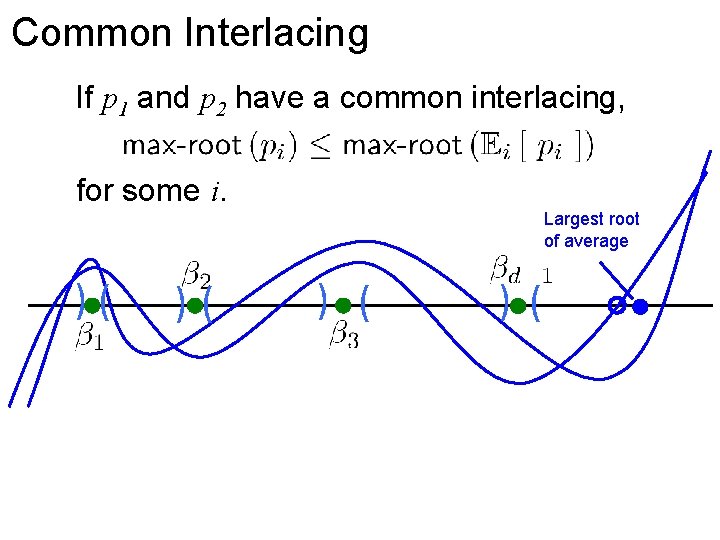
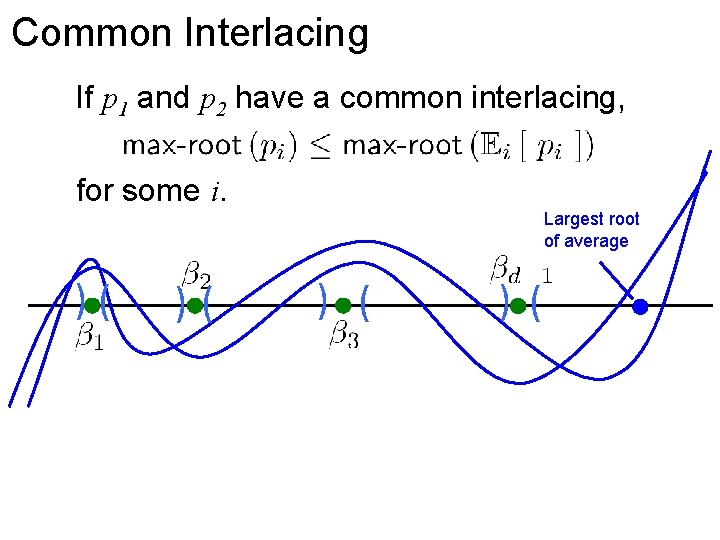
Common Interlacing If p 1 and p 2 have a common interlacing, for some i. Largest root of average )( )( ) ( )(

Common Interlacing If p 1 and p 2 have a common interlacing, for some i. Largest root of average )( )( ) ( )(

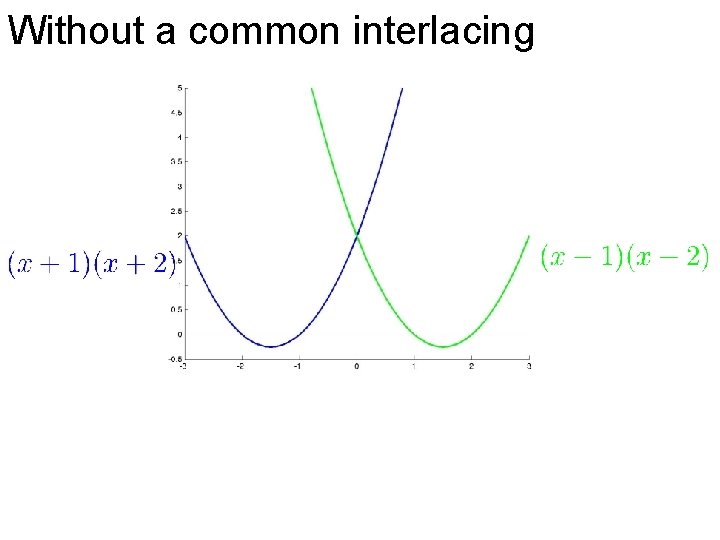
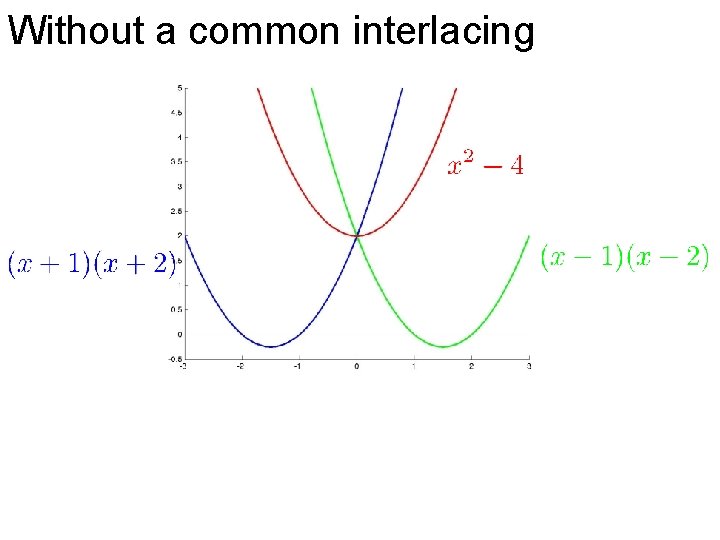
Without a common interlacing

Without a common interlacing

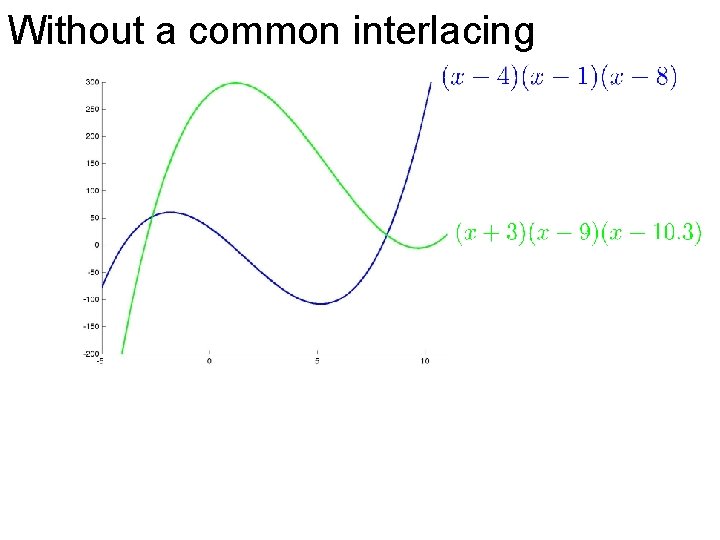
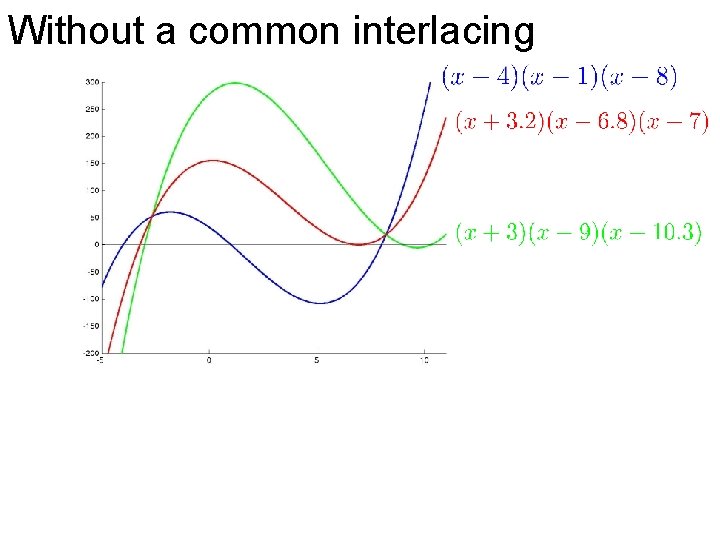
Without a common interlacing

Without a common interlacing

Common Interlacing If p 1 and p 2 have a common interlacing, for some i. Largest root of average )( )( ) ( )(

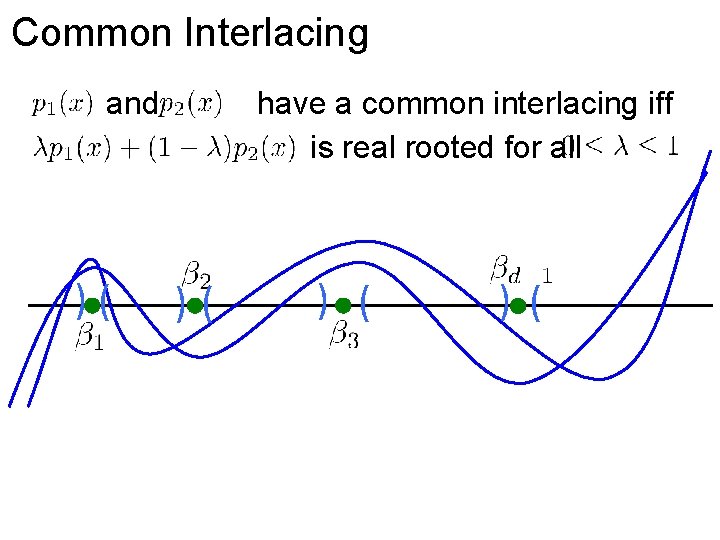
Common Interlacing and )( have a common interlacing iff is real rooted for all )( ) ( )(

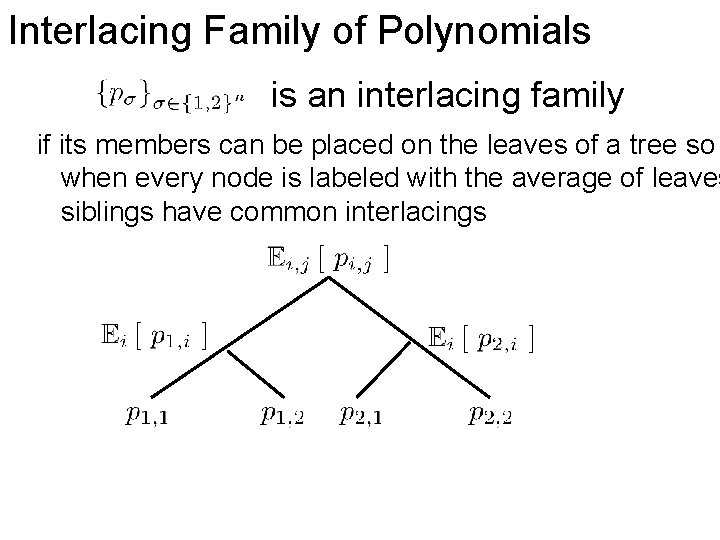
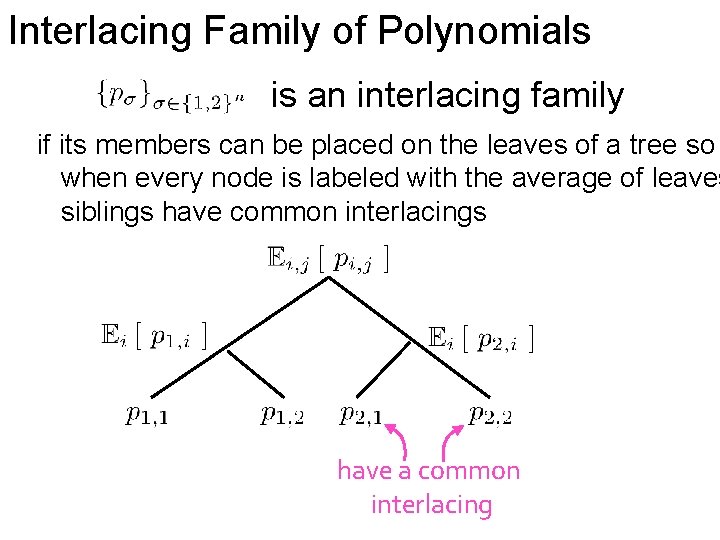
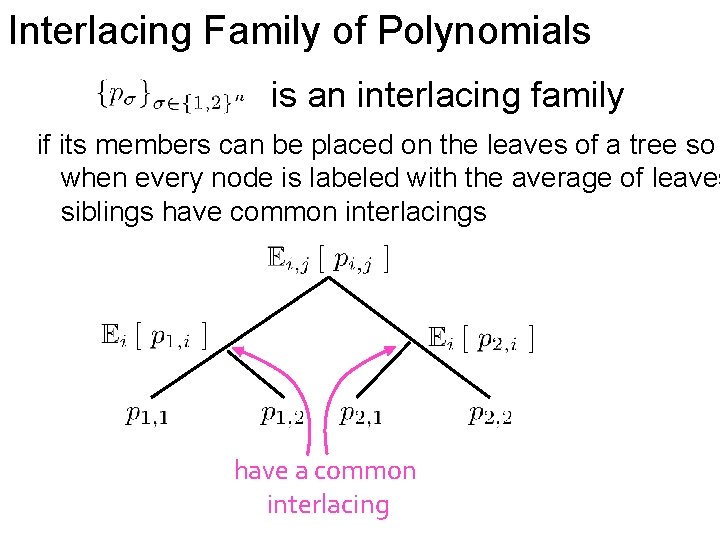
Interlacing Family of Polynomials is an interlacing family if its members can be placed on the leaves of a tree so when every node is labeled with the average of leaves siblings have common interlacings

Interlacing Family of Polynomials is an interlacing family if its members can be placed on the leaves of a tree so when every node is labeled with the average of leaves siblings have common interlacings have a common interlacing

Interlacing Family of Polynomials is an interlacing family if its members can be placed on the leaves of a tree so when every node is labeled with the average of leaves siblings have common interlacings have a common interlacing

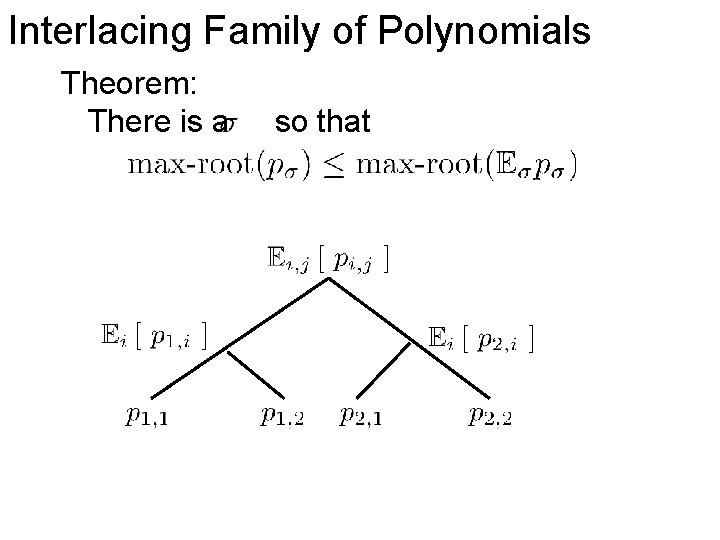
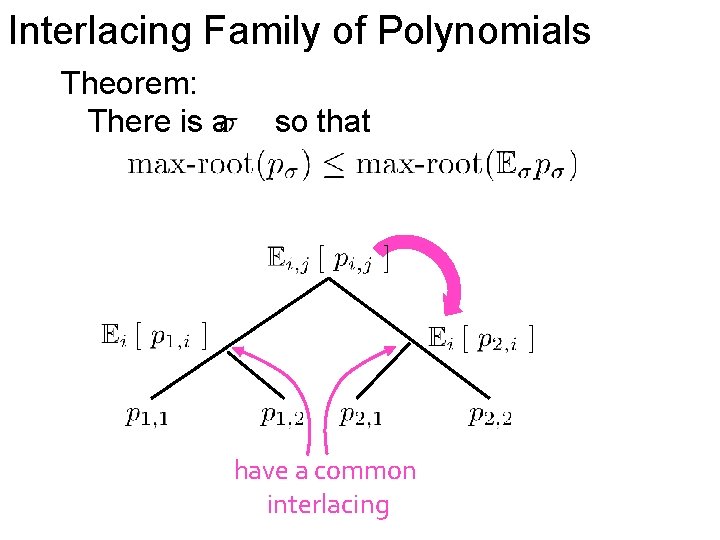
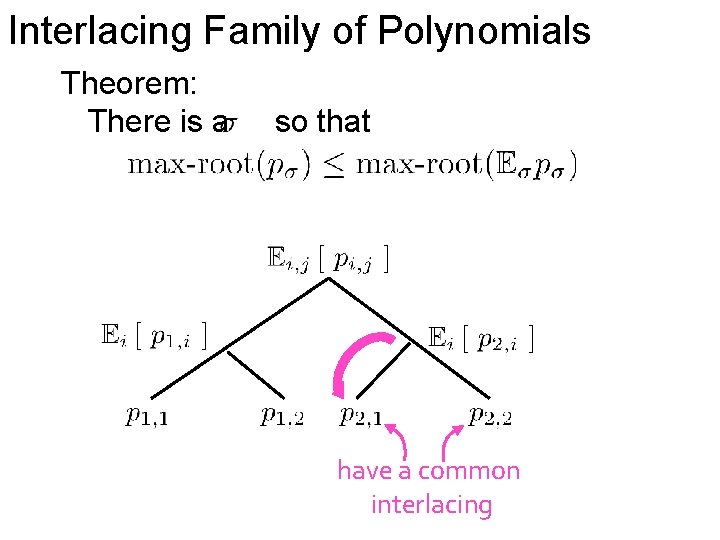
Interlacing Family of Polynomials Theorem: There is a so that

Interlacing Family of Polynomials Theorem: There is a so that have a common interlacing

Interlacing Family of Polynomials Theorem: There is a so that have a common interlacing

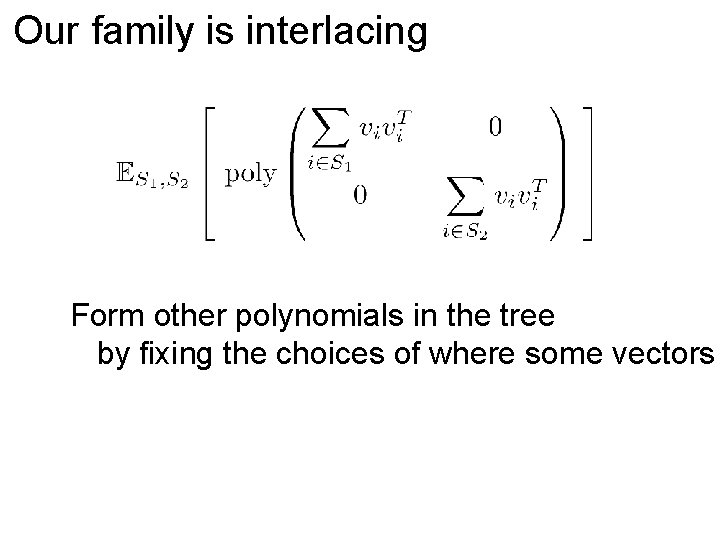
Our family is interlacing Form other polynomials in the tree by fixing the choices of where some vectors

Summary 1. Prove expected characteristic polynomial has real roots 2. Prove its largest root is at most 3. Prove is an interlacing family, so exists a partition whose polynomial has largest root at most

To learn more about Laplacians, see My class notes from “Spectral Graph Theory” and “Graphs and Networks” My web page on Laplacian linear equations, sparsification, etc. To learn more about Kadison-Singer Papers in Annals of Mathematics and survey from ICM. Available on ar. Xiv and my web page
 Daniel spielman spectral graph theory
Daniel spielman spectral graph theory Simulink matrix multiplication
Simulink matrix multiplication Ingrid spielman
Ingrid spielman Stephanie spielman osu
Stephanie spielman osu Spectral graph theory spielman
Spectral graph theory spielman Draw the graphs with the following adjacency matrices.
Draw the graphs with the following adjacency matrices. Testability tips in software testing
Testability tips in software testing Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Speed and velocity
Speed and velocity End behavior of polynomials
End behavior of polynomials Color vectors and viewpoint in still and moving images
Color vectors and viewpoint in still and moving images Ivory no.1 retainer uses
Ivory no.1 retainer uses Aims and objectives of matrices
Aims and objectives of matrices Applications of matrices and determinants
Applications of matrices and determinants Pam scoring
Pam scoring Homogeneous system of linear equations matrix
Homogeneous system of linear equations matrix Node reduction algorithm in software testing
Node reduction algorithm in software testing Blosum62
Blosum62 Identity matrix
Identity matrix Condition for matrix multiplication
Condition for matrix multiplication Determine whether each matrix product is defined
Determine whether each matrix product is defined Matrix all formula
Matrix all formula Persuasive communication theories
Persuasive communication theories Yale program for recovery and community health
Yale program for recovery and community health Partitioning a line segment formula
Partitioning a line segment formula A storm system moves 5000 km due east
A storm system moves 5000 km due east What are i and j in vectors
What are i and j in vectors Difference between vector and scalar
Difference between vector and scalar A vector has both location and direction.
A vector has both location and direction. Optr is a trapezium
Optr is a trapezium 2d motion equations
2d motion equations Scalar vs vector
Scalar vs vector Scalars and vectors
Scalars and vectors Linear algebra chapter 4 solutions
Linear algebra chapter 4 solutions Linearly dependent and independent vectors
Linearly dependent and independent vectors Vectors and the geometry of space
Vectors and the geometry of space Linear dependency
Linear dependency Dot product
Dot product Vectors form 3
Vectors form 3 Chapter 12 vectors and the geometry of space
Chapter 12 vectors and the geometry of space Properties of vector
Properties of vector Vectors trigonometry
Vectors trigonometry The diagram shows two vectors that point west and north.
The diagram shows two vectors that point west and north. Resolution and composition of vectors
Resolution and composition of vectors Collinear vectors
Collinear vectors Chapter 12 vectors and the geometry of space solutions
Chapter 12 vectors and the geometry of space solutions Physical quantities of vectors
Physical quantities of vectors Si unit of pressure
Si unit of pressure Antiparallel vectors
Antiparallel vectors A student adds two vectors with magnitudes of 200 and 40
A student adds two vectors with magnitudes of 200 and 40 Scalar triple product properties
Scalar triple product properties Technology applications teks
Technology applications teks Free fall
Free fall You are adding vectors of length 20 and 40 units
You are adding vectors of length 20 and 40 units Networks and graphs: circuits, paths, and graph structures
Networks and graphs: circuits, paths, and graph structures Tomer owns a daycare
Tomer owns a daycare Matrici progresive raven standard raspunsuri
Matrici progresive raven standard raspunsuri Inversa de la matriz identidad
Inversa de la matriz identidad Find the determinant of the following matrix:
Find the determinant of the following matrix: Can matrices be divided
Can matrices be divided Linear independence matlab
Linear independence matlab Wj-iv sentence writing fluency scoring
Wj-iv sentence writing fluency scoring Basic perinatal matrices
Basic perinatal matrices Matrices identidad
Matrices identidad ç
ç Matrix equation
Matrix equation 2*2 matrix
2*2 matrix What is i in matrix
What is i in matrix Matriz epistemologica
Matriz epistemologica Linear algebra for dummies
Linear algebra for dummies Multiplication of determinants
Multiplication of determinants Foote cone belding matrix
Foote cone belding matrix Clasificacion de matrices
Clasificacion de matrices Matrix multiplication dimensions
Matrix multiplication dimensions Inverse of a 3×3 matrix
Inverse of a 3×3 matrix Homogenous transformation matrices
Homogenous transformation matrices Subtract matrices calculator
Subtract matrices calculator Division de matrices 3x3
Division de matrices 3x3 Matriz fila concepto
Matriz fila concepto Concatenating vectors matlab
Concatenating vectors matlab Chapter 4 matrices answers
Chapter 4 matrices answers Augmented matrix
Augmented matrix Cuadro comparativo de matrices
Cuadro comparativo de matrices Aplicacion de estructuras de datos vectores y matrices
Aplicacion de estructuras de datos vectores y matrices Matrix multiplication associative property
Matrix multiplication associative property Transformations using matrices
Transformations using matrices Order of matrices
Order of matrices Matrices
Matrices Matrices equivalentes
Matrices equivalentes 3-6 solving systems using matrices
3-6 solving systems using matrices Leslie matrix
Leslie matrix Dimension u orden de una matriz
Dimension u orden de una matriz Matrices y determinantes
Matrices y determinantes Matrices in google docs
Matrices in google docs Det(a)
Det(a) Subtraction of matrices definition
Subtraction of matrices definition Partioned matrix
Partioned matrix Irreducible matrix
Irreducible matrix Shumezimi i dy matricave
Shumezimi i dy matricave Unit 1 algebra basics homework 6 matrices
Unit 1 algebra basics homework 6 matrices Solving equations calculator
Solving equations calculator Matrix algebra for dummies
Matrix algebra for dummies Matrices for dummies
Matrices for dummies Con las matrices n
Con las matrices n Matrices
Matrices Matrices
Matrices