Two Dimensional Motion and Vectors Vector Review Vector

Two Dimensional Motion and Vectors Vector Review Vector Analysis (Graphical) Vector Analysis (Analytical)

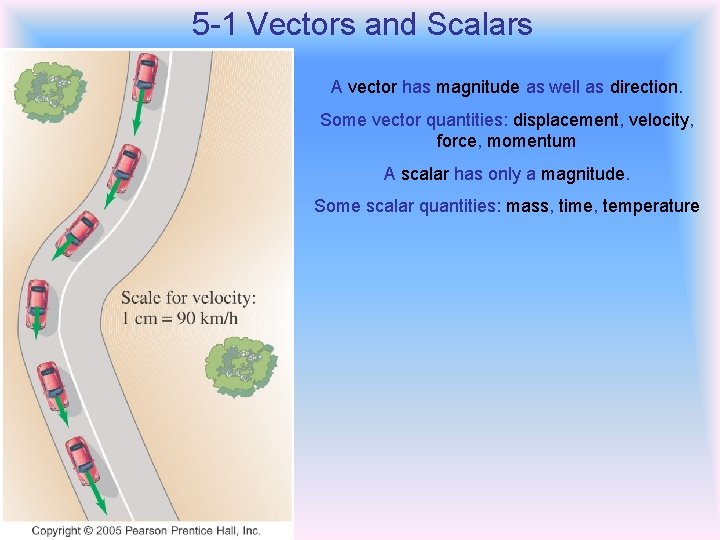
5 -1 Vectors and Scalars A vector has magnitude as well as direction. Some vector quantities: displacement, velocity, force, momentum A scalar has only a magnitude. Some scalar quantities: mass, time, temperature

Vectors can be drawn as arrows that are proportional to the magnitude. This is the graphical representation of a vector.

• Vectors can be added 2 ways. • 1. Graphically method (aka the “head-to-tail” method) • 2. component method • The sum of adding 2/more vectors is called the resolution vector.

It does not matter what order you add or subtract vectors, the resultant vector will be the same Resultant Vector A = 10 km and B = 20 km Both are acting to the right Vectors are drawn starting at a point (tail) and ending at an arrow pointing in the direction the vector is acting (head) Resultant Vector A = 10 km and B = 20 km A is acting to the right, B left Subtracting two vectors is the same as adding the opposite vector from above

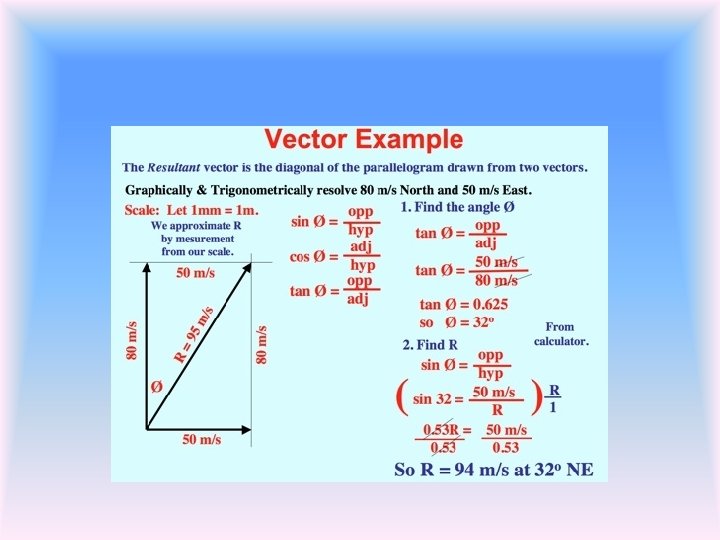
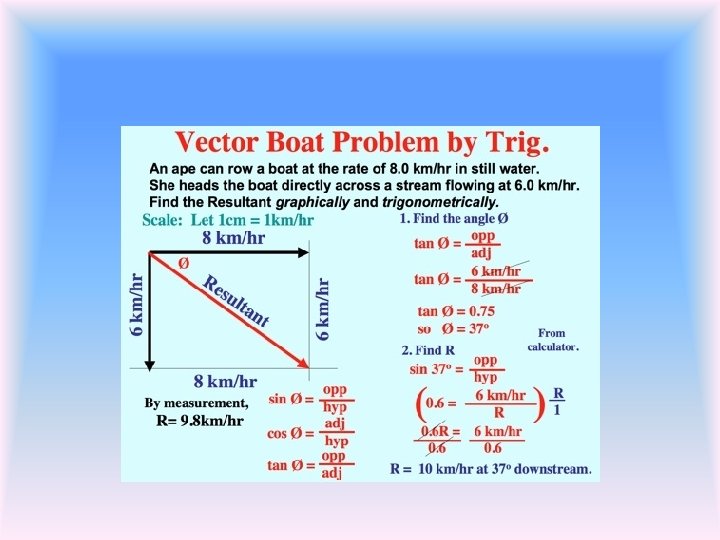
Physically Adding Vectors In the below left diagram, we see 3 vectors with their associated magnitudes and angles. In order to add these, we always must connect vectors 'head to tail' and the resultant vector (which represents the vector sum) is drawn from the tail of the first vector to the head of the last vector. In this example, using a ruler and protractor, we are able to get a resultant vector of about magnitude 11 and an angle of 102°.

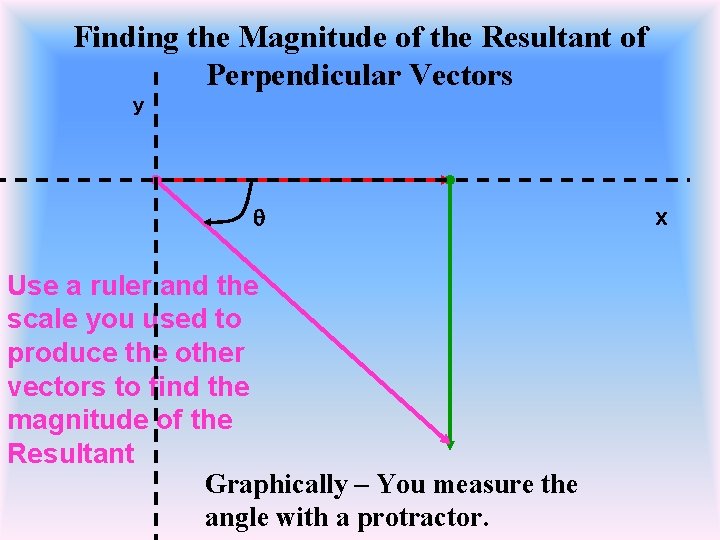
Finding the Magnitude of the Resultant of Perpendicular Vectors y q Use a ruler and the scale you used to produce the other vectors to find the magnitude of the Resultant Graphically – You measure the angle with a protractor. x

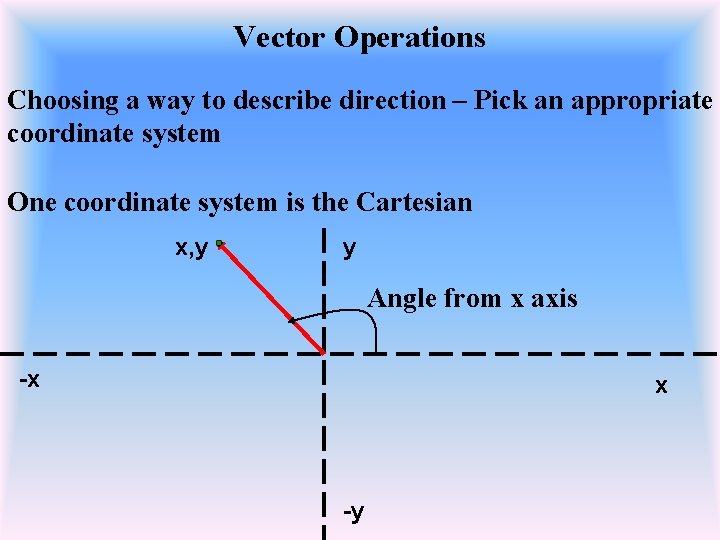
Vector Operations Choosing a way to describe direction – Pick an appropriate coordinate system One coordinate system is the Cartesian x, y y Angle from x axis -x x -y

NW NE SW SE Direction can be described by Compass points The angle from the x axis (or y axis) is 45 O The direction could also be described as 45 O north of east

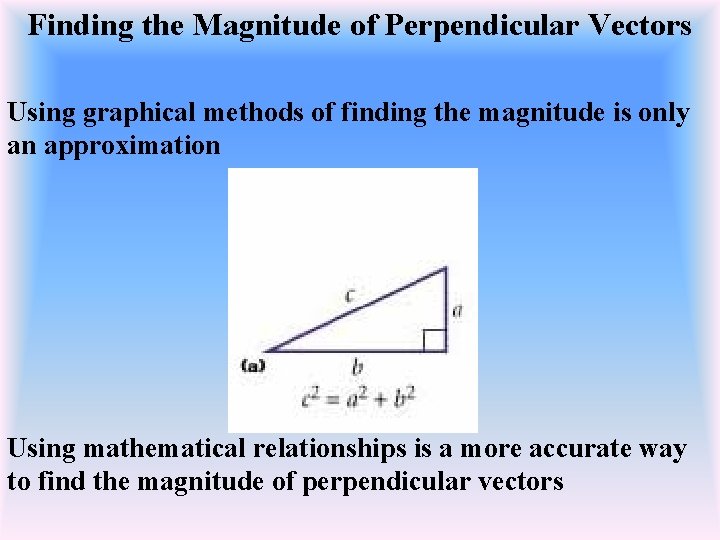
Finding the Magnitude of Perpendicular Vectors Using graphical methods of finding the magnitude is only an approximation Using mathematical relationships is a more accurate way to find the magnitude of perpendicular vectors

Finding the magnitude of displacement using the Pythagorean Theorem

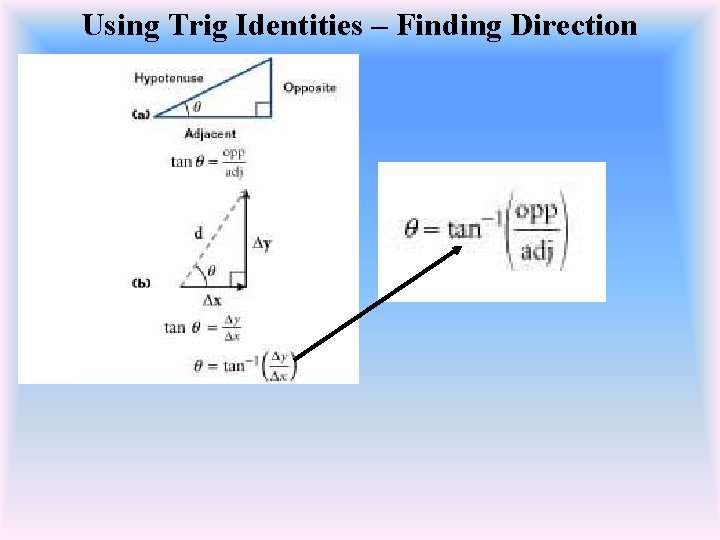
Using Trig Identities – Finding Direction

Great resource http: //hyperphysics. phyastr. gsu. edu/hbase/vect. html http: //www. physicsclassroom. com/class/ve ctors/U 3 L 1 b. cfm

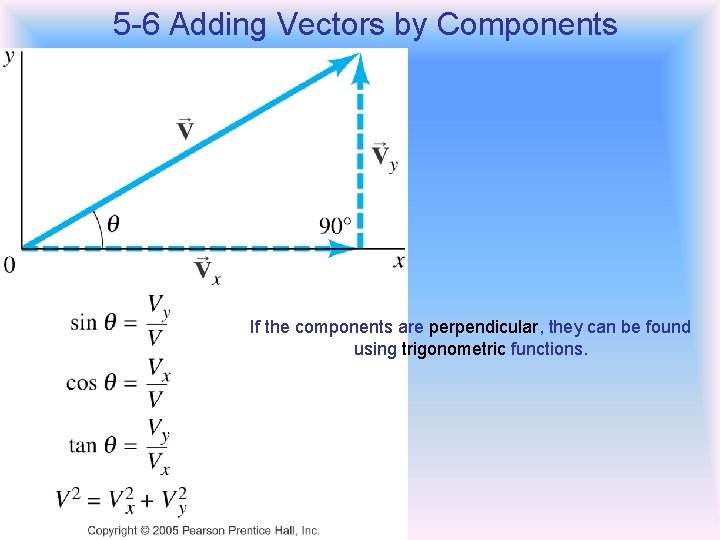
5 -6 Adding Vectors by Components If the components are perpendicular, they can be found using trigonometric functions.

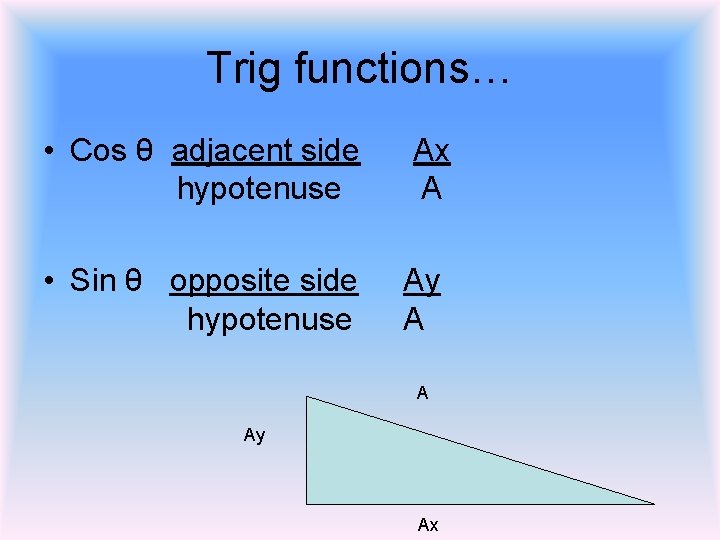
Trig functions… • Cos θ adjacent side Ax hypotenuse A • Sin θ opposite side Ay hypotenuse A A Ay Ax

Vr 15 m/s 6 m/s • Find Vr if its components are 15 N and 6 E. • Vr will be hypotenuse, so magnitude will be found Vr 2 = 152 + 62 = 16. 1 m/s • What will be the resulting angle?

• tan Θ = opp/adj tan Θ = arctan 15/6 = 68° Vr = 16. 1 units @ 68°

Vector addition • If 1 cm is equal to 20 km/hr and you draw the vectors, the north side is 5 cm and the east is 1 cm the resultant is 5. 099 cm. 100 km/hr north 20 km/hr east

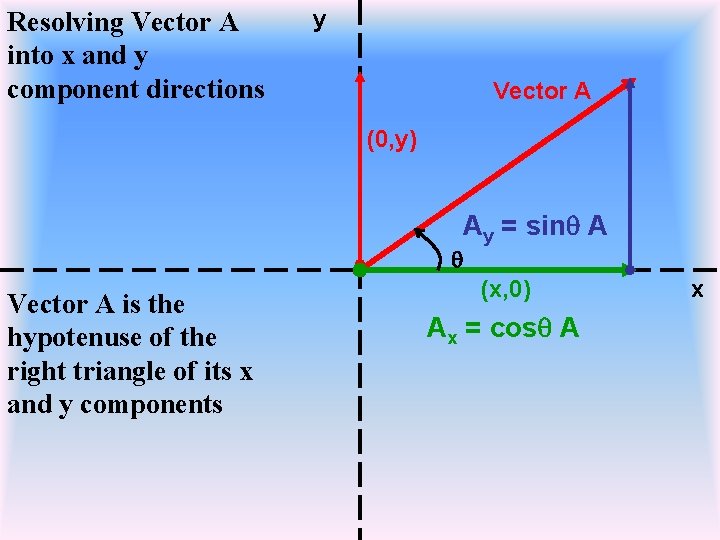
Resolving Vectors Into Components Vectors can be described by a set of INDEPENDENT perpendicular components with their proper units The “x” component lies parallel to the x axis The “y” component lies parallel to the y axis The components are call “projections” of the vector on the x and y axis. The x component has a magnitude of (x, 0) and the y component has a magnitude of (0, y)

Resolving Vector A into x and y component directions y Vector A (0, y) Ay = sinq A q Vector A is the hypotenuse of the right triangle of its x and y components (x, 0) Ax = cosq A x

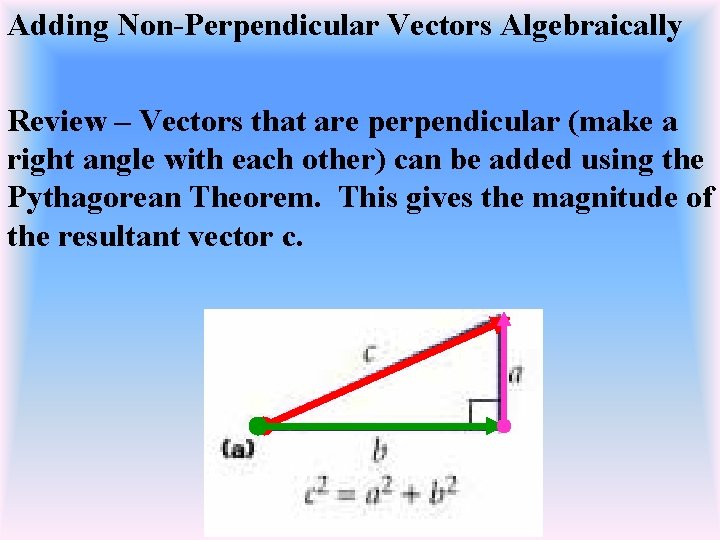
Adding Non-Perpendicular Vectors Algebraically Review – Vectors that are perpendicular (make a right angle with each other) can be added using the Pythagorean Theorem. This gives the magnitude of the resultant vector c.

• Using Trig to find components next easiest application. • What are the x and y components of a resultant vector 17. 5 m/s at 40° using sin and cos we can find the components sin 40 = Vy cos 40 = Vx 17. 5 (0. 6428)(17. 5) = N = 11. 2 y (0. 7660)(17. 5) = E = 13. 4 x

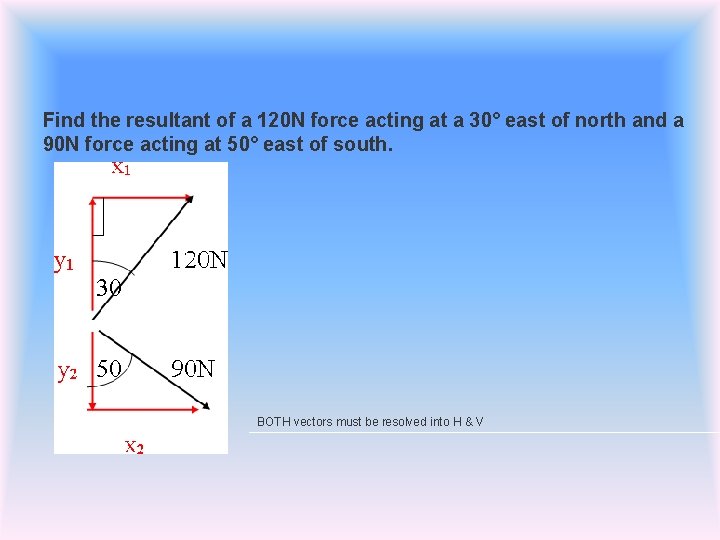
Find the resultant of a 120 N force acting at a 30° east of north and a 90 N force acting at 50° east of south. BOTH vectors must be resolved into H & V

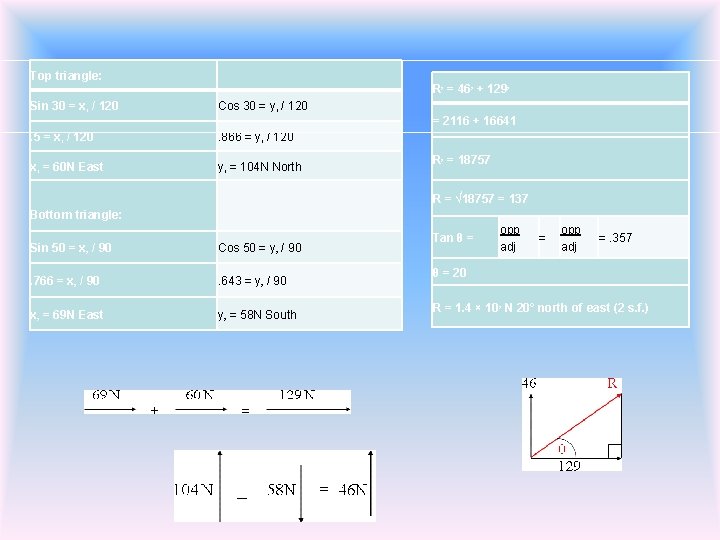
Top triangle: R = 46 + 129 2 Sin 30 = x / 120 1 2 2 Cos 30 = y / 120 1 = 2116 + 16641. 5 = x / 120 . 866 = y / 120 x = 60 N East y = 104 N North 1 1 Bottom triangle: 1 Cos 50 = y / 90 . 766 = x / 90 . 643 = y / 90 x = 69 N East y = 58 N South 2 2 2 R = √ 18757 = 137 Sin 50 = x / 90 2 R = 18757 1 Tan θ = 2 opp adj =. 357 θ = 20 2 2 R = 1. 4 × 10 N 20° north of east (2 s. f. ) 2

• Use the method of rectangular resolution to find the resultant of the • following set of forces: 1) 200 N to the right; • 2) 300 N @ 600 above the horizontal to the right. • 3) 100 N @ 450 above the horizontal to the left; • 4) 200 N vertically downward. vectors x-components y-components Suggestion: F 1 F 2 F 3 F 4 Fnet

The net force can be stated as: 279. 3 N to the right (x) & 130. 5 N upward (y). We can also determine the magnitude and direction. | Fnet | = = = 308. 3 N. The direction can be determined by redrawing the net force with it two components. From the figure we then have: tan = (130. 5(/(279. 3) =. 467 = 250. In words: The net force = 308. 3 N @ 250 above the horizontal to the right.

• http: //standards. nctm. org/document/eexa mples/chap 7/7. 1/part 2. htm • http: //phet. colorado. edu/simulations/sims. p hp? sim=Vector_Addition

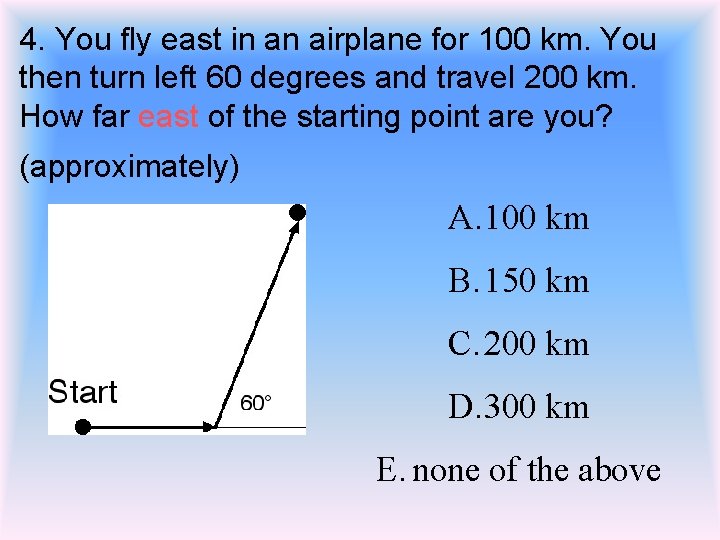
4. You fly east in an airplane for 100 km. You then turn left 60 degrees and travel 200 km. How far east of the starting point are you? (approximately) A. 100 km B. 150 km C. 200 km D. 300 km E. none of the above

C 200 km. x=100 km + (200 km)cos(60°)=100 km + 100 km = 200 km

And here is how to add two vectors after breaking them into x and y parts: The vector (8, 13) and the vector (26, 7) add up to the vector (34, 20) Example: add the vectors a = (8, 13) and b = (26, 7) c = a + b c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)

Let us add the two vectors head to tail: An Example Sam and Alex are pulling a box. • Sam pulls with 200 Newtons of force at 60° • Alex pulls with 120 Newtons of force at 45° as shown What is the combined force, and its direction?

Let us add the two vectors head to tail: Now, convert from polar to Cartesian (to 2 decimals): Sam's Vector: • x = r × cos( θ ) = 200 × cos(60°) = 200 × 0. 5 = 100 • y = r × sin( θ ) = 200 × sin(60°) = 200 × 0. 8660 = 173. 21 Alex's Vector: • x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0. 7071 = 84. 85 • y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0. 7071 = -84. 85

Now we have: Now it is easy to add them: (100, 173. 21) + (84. 85, -84. 85) = (184. 85, 88. 36)

We can convert that to polar for a final answer: • r = √ ( x 2 + y 2 ) = √ ( 184. 852 + 88. 362 ) = 204. 88 • θ = tan-1 ( y / x ) = tan-1 ( 88. 36 / 184. 85 ) = 25. 5° And we have this (rounded) result: And it looks like this for Sam and Alex:

Non-Perpendicular Vectors can be added by finding the x and y components of the vectors and adding or subtracting the one dimensional components Organizing these problems: Determine an appropriate coordinate system for the vectors Label the vectors Resolve all vectors into their x and y components List the x and y components of the vectors Add all of the x components of the vectors and all of the y components of the vectors The above yields the x and y components of the resultant vector

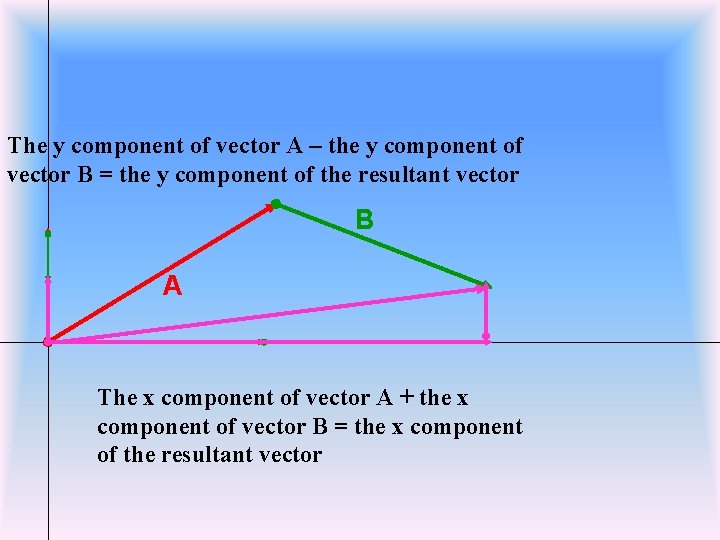
The y component of vector A – the y component of vector B = the y component of the resultant vector B A The x component of vector A + the x component of vector B = the x component of the resultant vector

Adding Two Dimensional Vectors y Remember, it does not matter what order you add the vectors, the resultant will be the same! D Resultant C B A The direction of the Resultant is from the X x axis q Draw the resultant vector from the tail of the first vector in the direction of the head of the last vector. The magnitude will be the length of the Resultant Vector.

• A plane flies 275 mi/hr at 215. 5° while a wind blows 95. 5 mi/hr west. Find the resultant velocity of the plane after 1 hour. Vpx = (cos 215. 5)(275 mi/hr) = -223. 9 mi/hr -224 mi/hr x or 224 mi/hr W Vpy = (sin 215. 5)(275 mi/hr) = -159. 7 mi/hr -160 mi/hr y or 160 mi/hr S Vw = 95. 5 W Vx= 224 W + 95. 5 W = 319. 5 W; Vy= 160 S Vr = 357 mi/hr at 207°

• A laser beam is aimed 15. 95° above the horizontal at a mirror 11, 648 m away. It glances off the mirror and continues for an additional 8570. m at 11. 44° above the horizon until it hits target. What is the resultant displacement of the beam to the target?

A laser beam is aimed 15. 95° above the horizontal at a mirror 11, 648 m away. It glances off the mirror and continues for an additional 8570. m at 11. 44° above the horizon until it hits target. What is the resultant displacement of the beam to the target? Vectors that are not at nice angles need to be dealt with. Break them up into their components. http: //physics. info/vector-components/practice. shtml

If the two vectors are NOT perpendicular to each other. • LAW OF SINES AND • LAW OF COSINES c a q A b • Looking for side c use the law of cosines: • Looking for <A use the law of sines. (<A is the smallest of the angles)

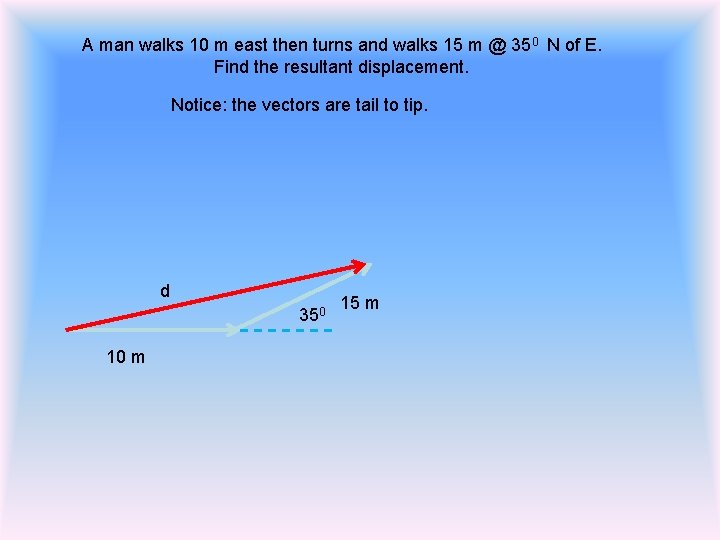
A man walks 10 m east then turns and walks 15 m @ 350 N of E. Find the resultant displacement. Notice: the vectors are tail to tip. d 350 10 m 15 m

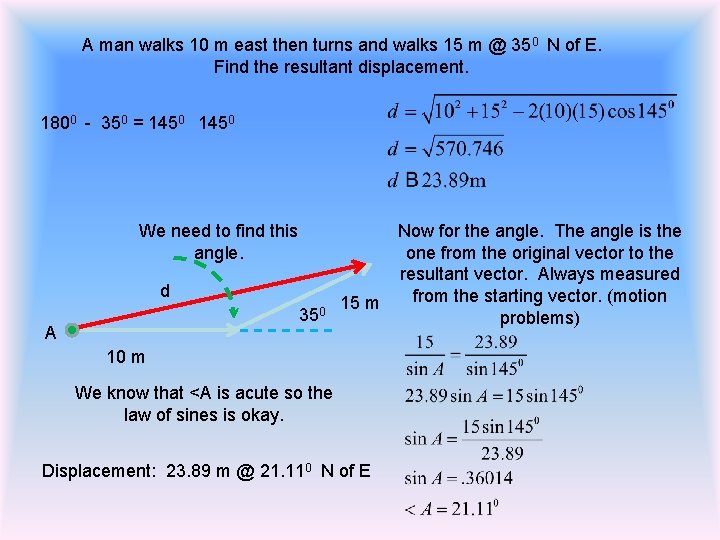
A man walks 10 m east then turns and walks 15 m @ 350 N of E. Find the resultant displacement. 1800 - 350 = 1450 We need to find this angle. d 350 A Now for the angle. The angle is the one from the original vector to the resultant vector. Always measured from the starting vector. (motion 15 m problems) 10 m We know that <A is acute so the law of sines is okay. Displacement: 23. 89 m @ 21. 110 N of E

What is a Projectile? Anything that is thrown or shot through the air. l Projectiles have velocities in two directions. l l Horizontal Motion: Motion parallel to the Earth’s surface. l Vertical Motion: The force of gravity pulling down on the object.

Horizontal Launched Projectiles Horizontally launched projectiles have an initial Vy of zero The objects velocity Vx is constant (gravity only affects objects that are moving up or down) Projectile motion is “free fall” motion with an initial Vx

Projectile Motion Objects that are thrown or launched into the air are accelerated by gravity and are projectiles In our problems, projectiles will ONLY be affected by gravity. The initial force to launch, air resistance while in flight, and the force used to stop the projectile are not considered part of the motion of the projectile The path of the projectile is parabolic and symmetrical Analyzing Projectile Motion is an application of vector components

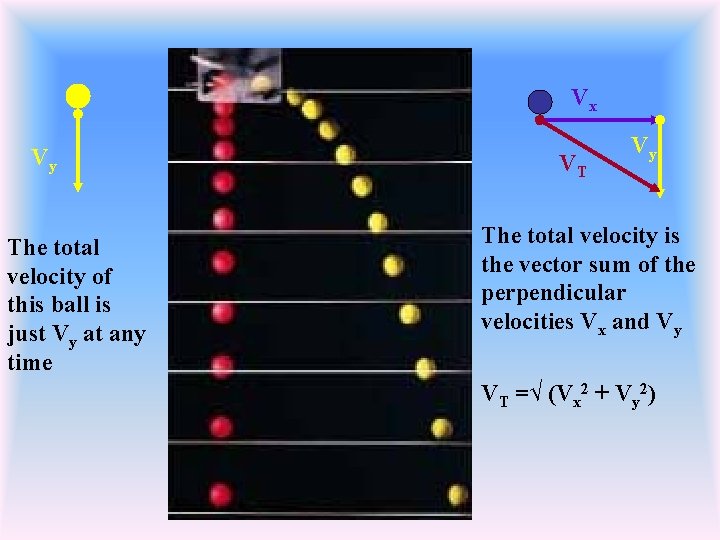
When objects fall, the Horizontal Velocity does not affect the Vertical Component because they are Perpendicular. If the purple ball is dropped at the same time the yellow ball falls off of the table …. . Vx …. . the objects fall at the same rate even though the purple ball Vy has a Horizontal Velocity Component Vx Vy They both will hit the floor at the same time.

WHAT VARIABLE IS THE SAME IN HORIZONTAL AND VERTICAL VELOCITY OF A PROJECTILE?

Projectiles…. . • http: //player. discoveryeducation. com/index. cfm? guid. Asset. Id=E 5 A 85 F 49 -ED 50 -42 B 694 DC 9249 BFF 423 D 3&bln. From. Search=1&produ ctcode=US

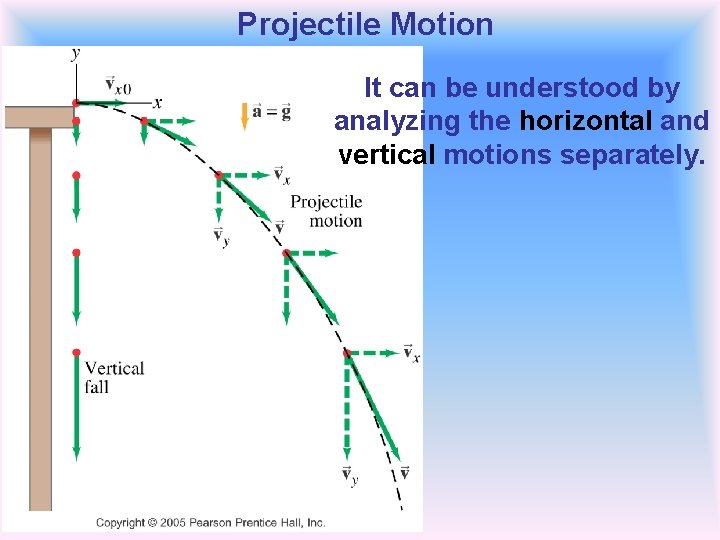
Projectile Motion It can be understood by analyzing the horizontal and vertical motions separately.

Projectile Motion The speed in the x-direction is constant; in the ydirection the object moves with constant acceleration g. This photograph shows two balls that start to fall at the same time. The on the right has an initial speed in the x-direction. It can be seen that vertical positions of the two balls are identical at identical times, while the horizontal position of the yellow ball increases linearly.

Vx Vy The total velocity of this ball is just Vy at any time VT Vy The total velocity is the vector sum of the perpendicular velocities Vx and Vy VT =√ (Vx 2 + Vy 2)

Any of these formulas can be used to solve the projectile motion problems VF 2 = Vo 2 + 2 a(Δd) Δd = Vo Δt + ½ a (t 2) Vf = Vo + aΔt

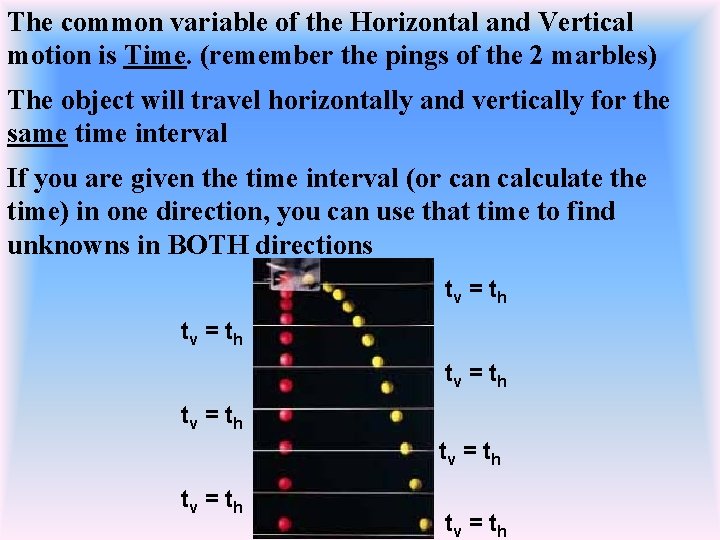
The common variable of the Horizontal and Vertical motion is Time. (remember the pings of the 2 marbles) The object will travel horizontally and vertically for the same time interval If you are given the time interval (or can calculate the time) in one direction, you can use that time to find unknowns in BOTH directions tv = th tv = th

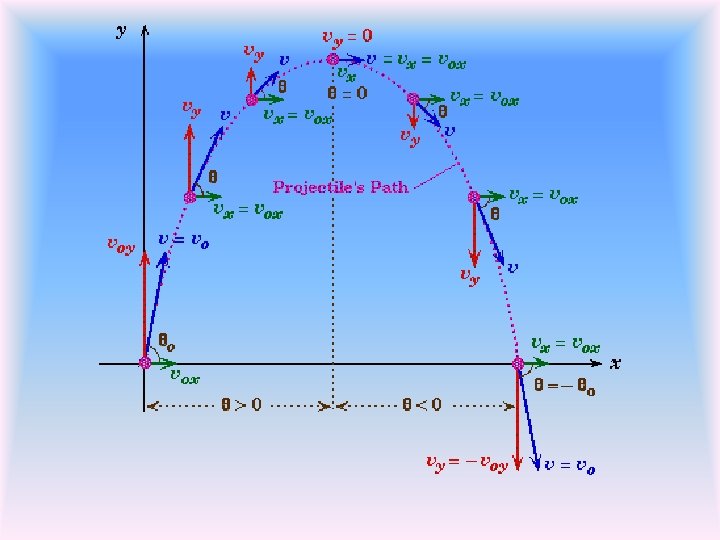
Projectiles Launched at an Angle The initial vertical velocity, Vy of the projectile is not zero The velocity in the x direction, Vx is constant for the entire flight The total velocity, VT of the projectile is the vector sum of the perpendicular Vx and Vy velocities (at any point in the projectile’s path)

Analyzing Projectile Motion With Velocity Vectors After the cannon ball is launched, the ball’s Horizontal Velocity Component remains constant. No force is acting in the horizontal direction. Notice the path of the ball is SYMETRICAL with no air resistance. This is important to remember when solving problems. Vy Vx However, gravity decreases the Vertical Component as it rises until it is 0, and it increases in the downward direction as it falls.

Practice Problem 1 • In her Physics lab, Melanie rolls a 10 g marble down a ramp and off the table with a horizontal velocity of 1. 2 m/s. The marble falls in a cup placed. 51 m from the table’s edge. How high is the table?

And the answer is • First find the time in the air (same time for vertical and horizontal) – t = dx / vx – . 51 m /1. 2 m/s =. 43 s – Since things fall at the same rate…. . you can use the same time to find the vertical distance it traveled. – Δdy = vyΔt + ½ gt 2 – Δdy = ½ (-9. 8 m/s 2) (. 43 s)2 = -. 9 m

Example 2: A baseball is hit with a horizontal speed of 25 m/s. What is its position and velocity after 2 s? x +50 m 25 m/s y -19. 6 m First find horizontal and vertical displacements: x = 50. 0 m y = -19. 6 m

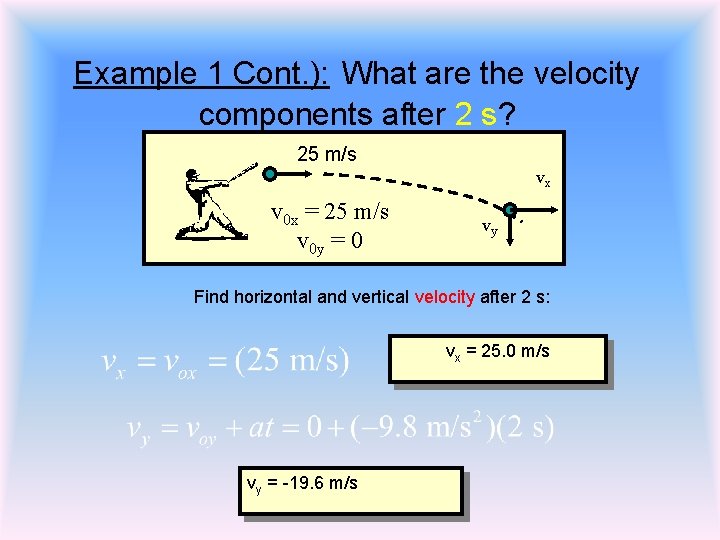
Example 1 Cont. ): What are the velocity components after 2 s? 25 m/s vx v 0 x = 25 m/s v 0 y = 0 vy Find horizontal and vertical velocity after 2 s: vx = 25. 0 m/s vy = -19. 6 m/s

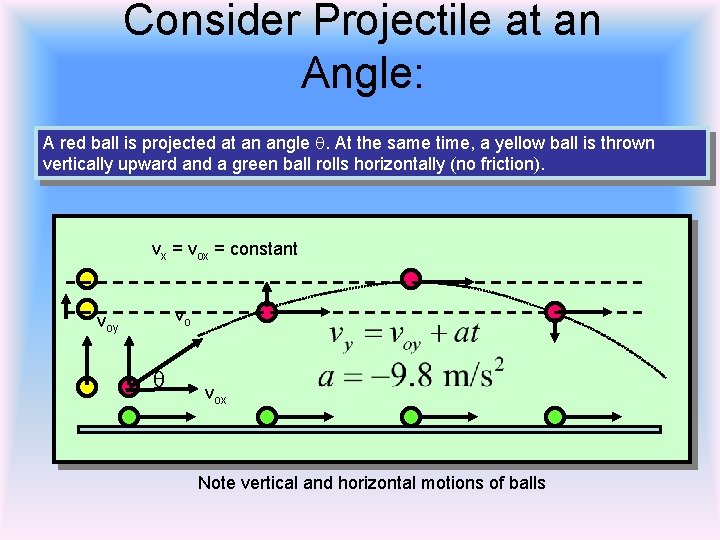
Consider Projectile at an Angle: A red ball is projected at an angle q. At the same time, a yellow ball is thrown vertically upward and a green ball rolls horizontally (no friction). vx = vox = constant vo voy q vox Note vertical and horizontal motions of balls

Displacement Calculations For General Projection: The components of displacement at time t are: For projectiles: Thus, the displacement components x and y for projectiles are:

Velocity Calculations For General Projection: The components of velocity at time t are: For projectiles: Thus, the velocity components vx and vy for projectiles are:

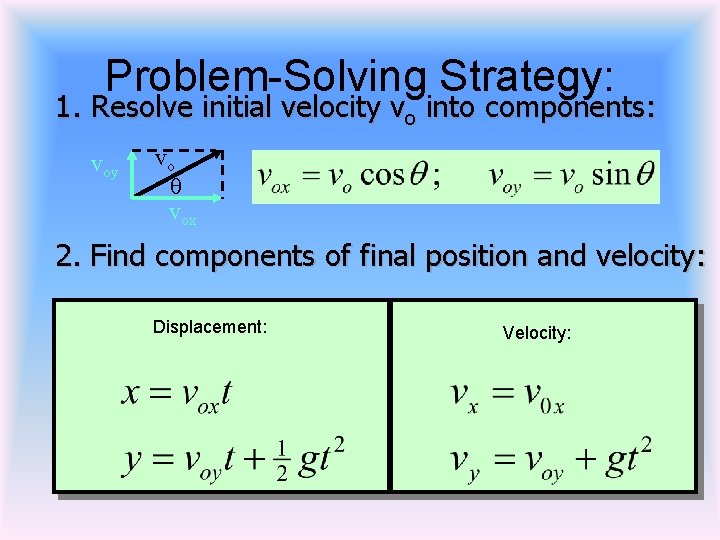
Problem-Solving Strategy: 1. Resolve initial velocity vo into components: voy vo q vox 2. Find components of final position and velocity: Displacement: Velocity:

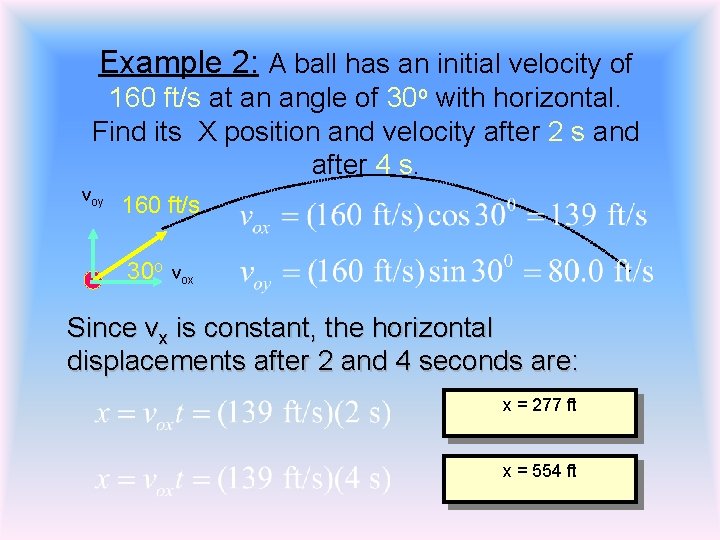
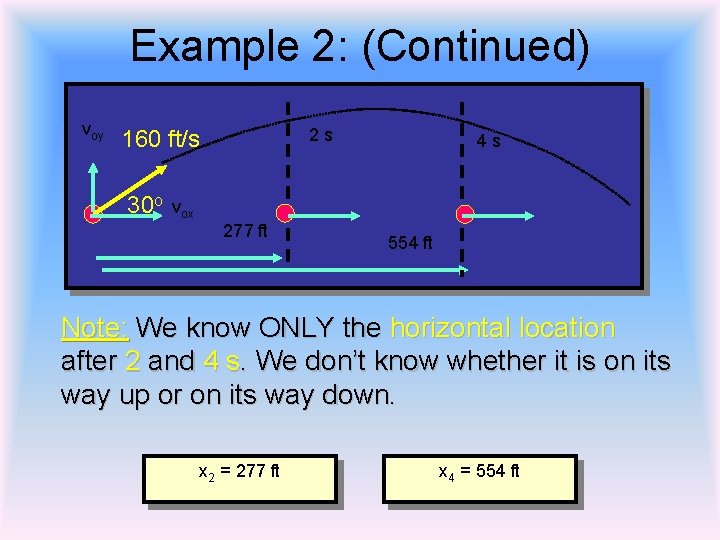
Example 2: A ball has an initial velocity of 160 ft/s at an angle of 30 o with horizontal. Find its X position and velocity after 2 s and after 4 s. voy 160 ft/s 30 o vox Since vx is constant, the horizontal displacements after 2 and 4 seconds are: x = 277 ft x = 554 ft

Example 2: (Continued) voy 2 s 160 ft/s 30 o 4 s vox 277 ft 554 ft Note: We know ONLY the horizontal location after 2 and 4 s. We don’t know whether it is on its way up or on its way down. x 2 = 277 ft x 4 = 554 ft

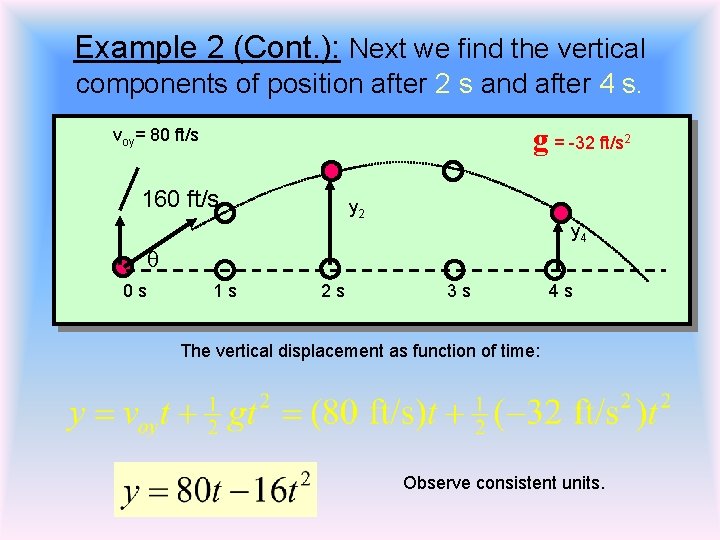
Example 2 (Cont. ): Next we find the vertical components of position after 2 s and after 4 s. g = -32 ft/s voy= 80 ft/s 2 160 ft/s y 2 y 4 q 0 s 1 s 2 s 3 s 4 s The vertical displacement as function of time: Observe consistent units.

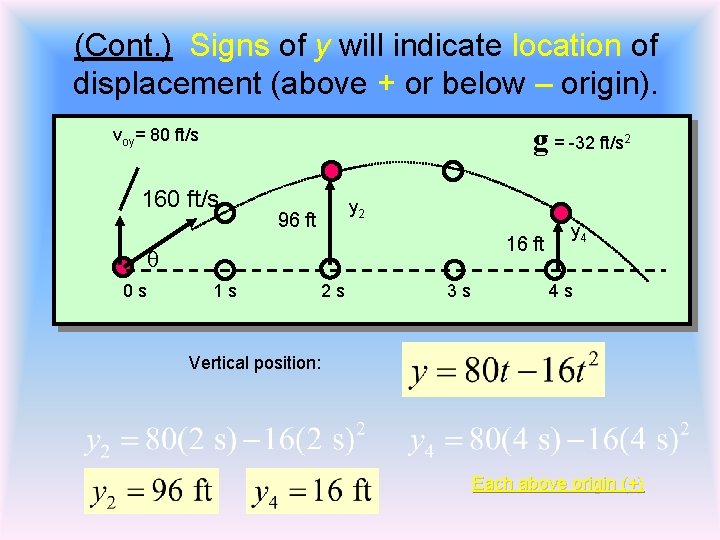
(Cont. ) Signs of y will indicate location of displacement (above + or below – origin). g = -32 ft/s voy= 80 ft/s 2 160 ft/s y 2 96 ft 16 ft q 0 s 1 s 2 s 3 s y 4 4 s Vertical position: Each above origin (+)

(Cont. ): Next we find horizontal and vertical components of velocity after 2 and 4 s. voy 160 ft/s 30 o vox Since vx is constant, vx = 139 ft/s at all times. Vertical velocity is same as if vertically projected: At any time t:

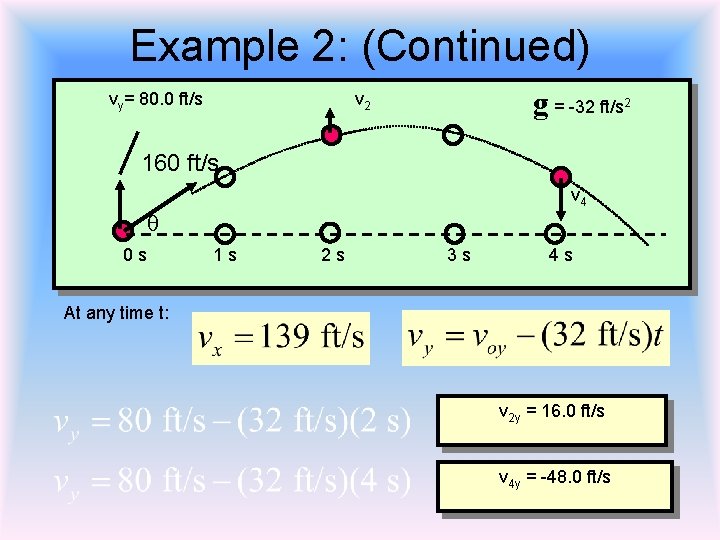
Example 2: (Continued) vy= 80. 0 ft/s g = -32 ft/s v 2 2 160 ft/s v 4 q 0 s 1 s 2 s 3 s 4 s At any time t: v 2 y = 16. 0 ft/s v 4 y = -48. 0 ft/s

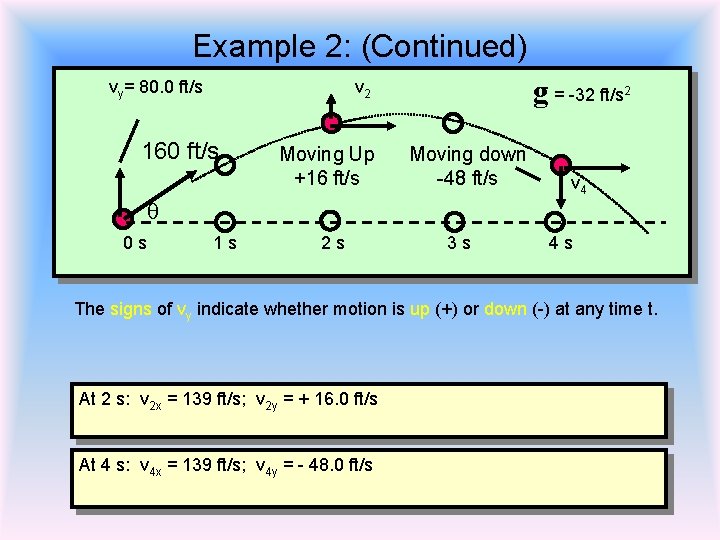
Example 2: (Continued) vy= 80. 0 ft/s g = -32 ft/s v 2 160 ft/s Moving Up +16 ft/s 2 Moving down -48 ft/s q 0 s 1 s 2 s 3 s v 4 4 s The signs of vy indicate whether motion is up (+) or down (-) at any time t. At 2 s: v 2 x = 139 ft/s; v 2 y = + 16. 0 ft/s At 4 s: v 4 x = 139 ft/s; v 4 y = - 48. 0 ft/s

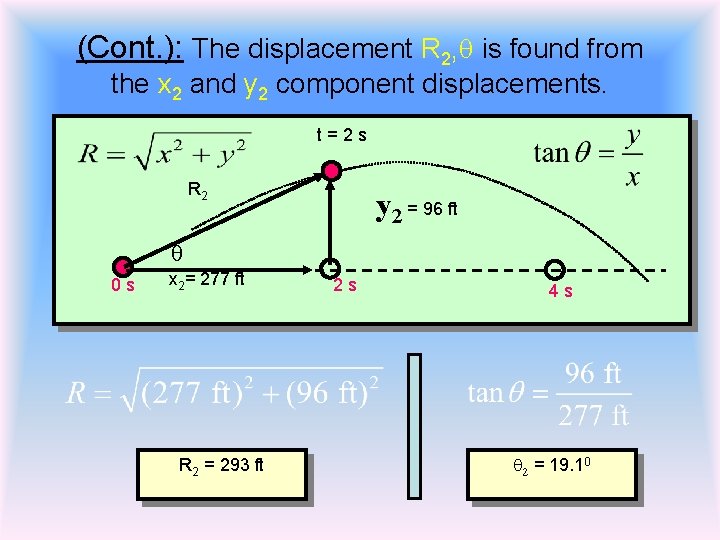
(Cont. ): The displacement R 2, q is found from the x 2 and y 2 component displacements. t = 2 s R 2 y 2 = 96 ft q 0 s x 2= 277 ft R 2 = 293 ft 2 s 4 s q 2 = 19. 10

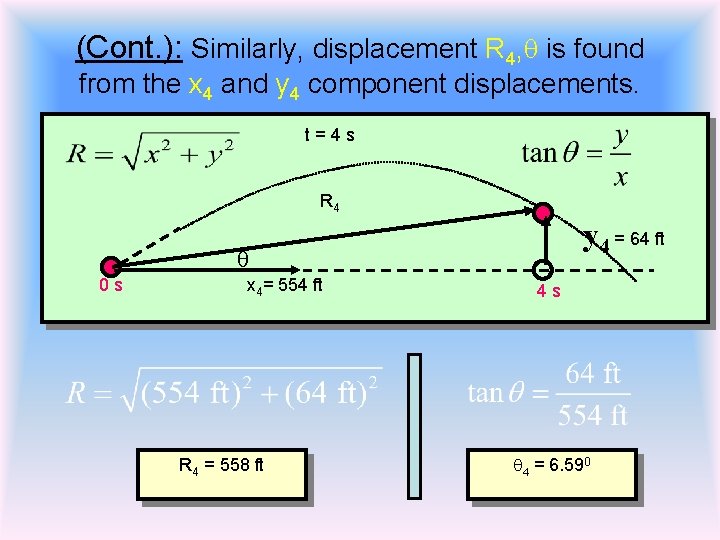
(Cont. ): Similarly, displacement R 4, q is found from the x 4 and y 4 component displacements. t = 4 s R 4 y 4 = 64 ft q 0 s x 4= 554 ft R 4 = 558 ft 4 s q 4 = 6. 590

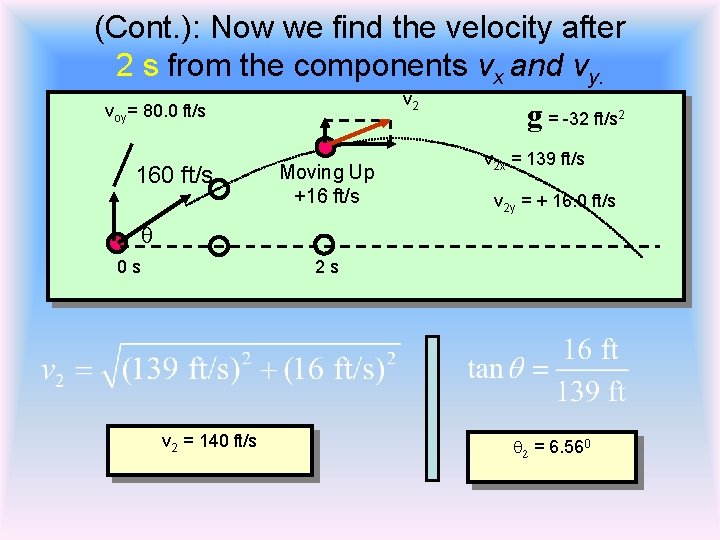
(Cont. ): Now we find the velocity after 2 s from the components vx and vy. v 2 voy= 80. 0 ft/s 160 ft/s Moving Up +16 ft/s g = -32 ft/s 2 v 2 x = 139 ft/s v 2 y = + 16. 0 ft/s q 0 s 2 s v 2 = 140 ft/s q 2 = 6. 560

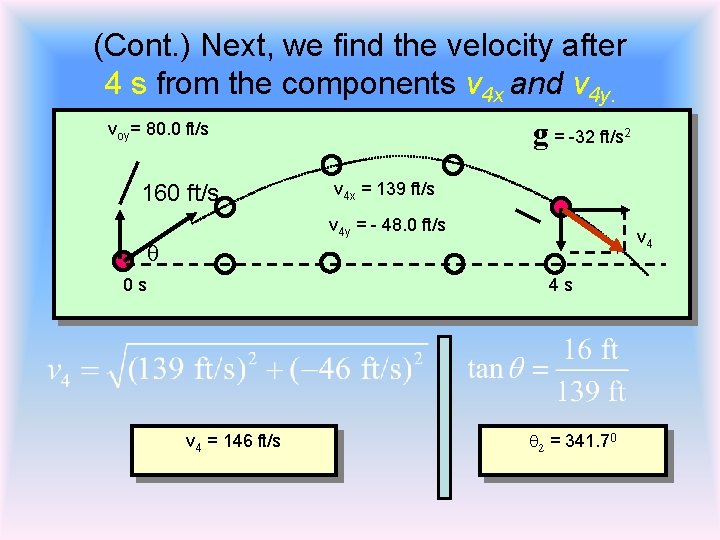
(Cont. ) Next, we find the velocity after 4 s from the components v 4 x and v 4 y. g = -32 ft/s voy= 80. 0 ft/s 160 ft/s 2 v 4 x = 139 ft/s v 4 y = - 48. 0 ft/s q 0 s v 4 4 s v 4 = 146 ft/s q 2 = 341. 70

An arrow is shot at a 30. 0° angle above horizontal ground. It has an initial speed of 49 m/s. (a) How high will the arrow go? (b) What horizontal distance will it travel? a. 31 m b. 210 m

2 D Projectile Motion The kinematics equations mentioned in the previous slide are as follows: 1. 2. 3. 4. 5. vix = vi (cos θ) = constant (x direction, a = 0) dx = vi (cos θ) t (x direction, a = 0) vyf = vi (sin θ) + a t (y direction, a = g) vyf 2 = vi 2 (sin θ) 2 + 2 a dy (y direction, a = g) dy = vi (sin θ) t + ½ a t 2 (y direction, a = g)

2 D Projectile Motion Example One (projectile launched at an angle): A projectile is launched at 50 m/s at an angle of 45 o from the horizontal. It lands at a place level with the place that it was launched from. Find: a. time of flight of the projectile (t total = ? ) b. maximum height of the projectile (dy = ? ) c. range of the projectile (dx = ? ) 2 given: a = – 9. 8 m/s s / m o 0 v = 50 m/s, θ = 45 i 5 = v i θ θ = 45 o vix = vi (cos θ) viy = vi (sin θ)

2 D Projectile Motion a. b. time of flight (t) dy = vi (sin θ) t + ½ a t 2 (know that dy = 0) – vi (sin θ) t = ½ a t 2 (dy = displacement) – vi (sin θ) = ½ a t – 2(vi sin θ) = – 2(50 m/s)(. 7071) = 7. 2 s = t t = a – 9. 8 m/s 2 maximum height (dy) dy = vi (sin θ) t + ½ a t 2 (use t / 2) = (50 m/s)(. 7071)(3. 6 s) + (½)(– = (50 m/s)(. 7071)(3. 6 s) + (½)( 9. 8 m/s 2)(3. 6 s) 2 = 63. 7 m = d y could have used v 2 = v 2 (sin θ) 2 + 2 a d yf yi y

2 D Projectile Motion c. Range (dx) = ? dx = vx t (substitute: 1. vx = vi cos θ) dx = (vi cos θ) t dx = (50 m/s)(. 7071)(7. 2 s) dx = 254. 5 m

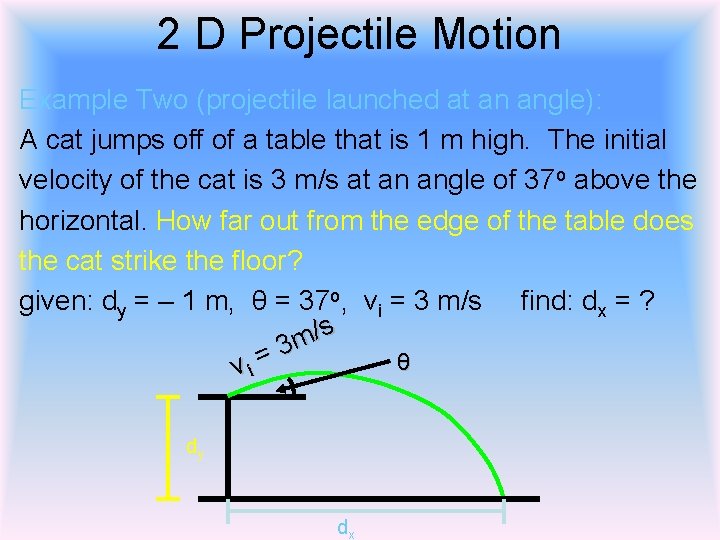
2 D Projectile Motion Example Two (projectile launched at an angle): A cat jumps off of a table that is 1 m high. The initial velocity of the cat is 3 m/s at an angle of 37 o above the horizontal. How far out from the edge of the table does the cat strike the floor? given: dy = – 1 m, θ = 37 o, vi = 3 m/s find: dx = ? /s m 3 = θ vi dy dx

2 D Projectile Motion 1. First, find the horizontal and vertical components of the initial velocity. viy = vi (sin 37 o) = 3 m/s (sin 37 o) = 1. 8 m/s = viy vix = vi (cos 37 o) = 3 m/s (cos 37 o) = 2. 4 m/s = vix 2. Use this equation to solve for t because t is the only unknown. dy = vi (sin θ) t + ½ a t 2 Since dy is not = 0, the only way to solve for t is to use the quadratic equation. a. ½ a t 2 + viy t + – t + dy = 0

2 D Projectile Motion a. ½ a t 2 + viy t + – t + dy = 0 b. (½ (– 9. 8 m/s 2)) t 2 + (1. 8 m/s) t + (+ 1 m) = 0 (a) (b) (c) – b +/– √b 2 – 4 a c (quadratic equation) 2 a – 1. 8 m/s +/– √(1. 8 m/s) 2 – {4(– 4. 9 m/s 2)(+1 m)} c. t = 2(– 4. 9 m/s 2) d. t = 0. 67 seconds

2 D Projectile Motion Then plug t into this equation to finally find dx. dx = vi (cos θ) t dx = (2. 4 m/s)(0. 67 s) dx = 1. 6 m

A daredevil tries to jump a canyon of width 10 m. To do so, he drives his motorcycle up an incline sloped at an angle of 15 degrees. What minimum speed is necessary to clear the canyon?

vx = Dx / Dt = V cos 15 o vy = V sin 15 o V = 10 m / (. 73 s) * cos 15 o) V = 14. 18 m/s, the minimum speed needed for success.

A brick is thrown upward from the top of a building at an angle of 25 degrees above the horizontal and with an initial speed of 15 m/s. If the brick is in the air for 3 seconds, how high is the building? Find the initial vertical velocity: sin 25 o = Vy/15 m/s Vy = 6. 3 m/s Now use the y-component information to find the height: Dy = (. 5)(g)(t 2) + (Vy (t) Dy = (. 5)(-9. 8 m/s 2)(3 s) 2+(6. 3 m/s)(3 s) Dy = -45 m +18. 9 m Dy = -25. 2 m

A brick is thrown upward at an angle of 25 degrees above the horizontal and with an initial speed of 15 m/s. How FAR in the horizontal direction did the brick land from the where it was released? Cos 25° (15) = Vx Vf = V 0 + g t 13. 6 = Vx 0= 6. 3 + (-9. 8) t Sin 25° (15) = Vy T =. 65 sec Vy = 6. 3 for the time UP so the total time in the air is 1. 3 seconds. v. X = dx/t 13. 6 = dx/1. 3 dx = 17. 6 m

An arrow is shot at a 30. 0° angle above horizontal ground. It has an initial speed of 49 m/s. (a) How high will the arrow go? (b) What horizontal distance will it travel? Find Vx and Vy Cos 30 (49)= 42. 4= Vx Sin 30 (49) 24. 5= Vy VF 2 = Vo 2 + 2 a(Δd) 0 = 24. 5 2 + 2 (-9. 8) d Dy= 30. 625

Now part B knowing that Vx= 42. 4 and we are looking for dx. Vf = V 0 + g t 0= 24. 5 + (-9. 8) t T = 2. 5 sec for the time UP so the total time in the air is 5 seconds. Now solve for dx Vx = dx/ t 42. 4 = dx/5 Dx= 212 m

Billy jumps off a high diving platform with a horizontal velocity of 2. 06 m/s and lands in the water 1. 3 seconds later. How high is the platform? 8. 21 m A model rocket flies horizontally off the edge of a cliff at a velocity of 50. 0 m/s. If the canyon below is 100. 0 m deep, how far from the edge of the cliff does the model rocket land? 225 m A stone is thrown horizontally from the top of a 40. 00 m cliff. The stone lands at a distance of 25. 00 m from the edge of the cliff. What is the time needed to hit the ground and the initial horizontal velocity of the stone? A boy kicks a football with an initial horizontal velocity of 14 m/s and 7 m/s initial vertical velocity. What is the highest elevation reached by the football in its trajectory? 2. 5 m 2. 9 sec, 8. 75 m/s

A ball rolls over the edge of a table with a horizontal velocity in m/s. The height of the table is 1. 6 m and the horizontal range of the ball from the base of the table is 20 m. What is the initial speed of the ball? 35 m/s