MATRICES Matrices A matrix is a rectangular array

MATRICES

Matrices • A matrix is a rectangular array of objects (usually numbers) arranged in m horizontal rows and n vertical columns. • A matrix with m rows and n columns is called an m x n matrix. Example: The matrix is a 3 x 2 matrix. • The plural of matrix is matrices. • The ith row of A is the 1× n matrix [ai 1, ai 2, …, ain], 1≤ i ≤ m. The jth column of A is the m × 1 matrix: , 1≤ j ≤ n. 2

Matrices • We refer to the element in the ith row and jth column of the matrix A as aij or as the (i, j) entry of A, and we often write it as A= [aij ]. • A matrix with the same number of rows as columns is called square matrix, whose order is n. 2 2 • Two matrices are equal if they have the same number of rows and the same number of columns and the corresponding entries in every position are equal. 3

Example 1 Then A is 2 x 3 with a 12 = 3 and a 23 = 2, B is 2 x 2 with b 21 = 4, C is 1 x 4, D is 3 x 1, and E is 3 x 3 4

Diagonal Matrix A square matrix A = [aij ] for which every entry off the main diagonal is zero, that is, aij = 0 for i ≠ j, is called a diagonal matrix Example 5

Example of Matrix applications • Matrices are used in many applications in computer science, and we shall see them in our study of relations and graphs. • At this point, we present the following simple application showing how matrices can be used to display data in a tabular form 6

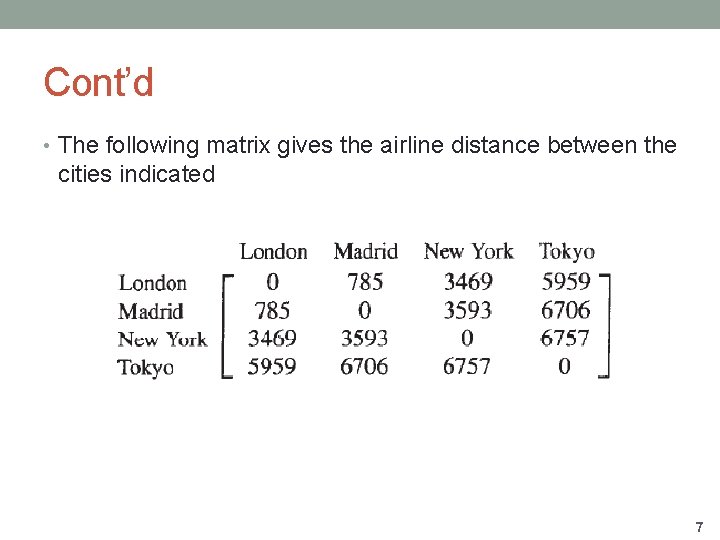
Cont’d • The following matrix gives the airline distance between the cities indicated 7

Matrix Equality • Two m x n matrices A = [aij ] and B = [bij] are said to be equal if aij = bij , 1 ≤ i ≤ m, 1 ≤ j ≤ n; that is, if corresponding elements in every position are the same. 8

Cont’d If Then A = B if and only if x=-3, y=0, and z=6 9

Matrix Arithmetic DEFINITION 3: Let A = [aij] and B = [bij] be m x n matrices. The sum of A and B, denoted by: A + B, is the m x n matrix that has aij + bij as its ( i, j )th element. In other words, A + B = [aij + bij]. • The sum of two matrices of the same size is obtained by adding elements in the corresponding positions. • Matrices of different sizes cannot be added. 10

Example 1 Example 2 11

Zero Matrix • A matrix all of whose entries are zero is called: a zero matrix and is denoted by 0 • Each of the following is Zero matrix: 12

Properties of Matrix Addition • A+B=B+A • (A + B) + C = A + (B + C) • A+0=0+A=A 13

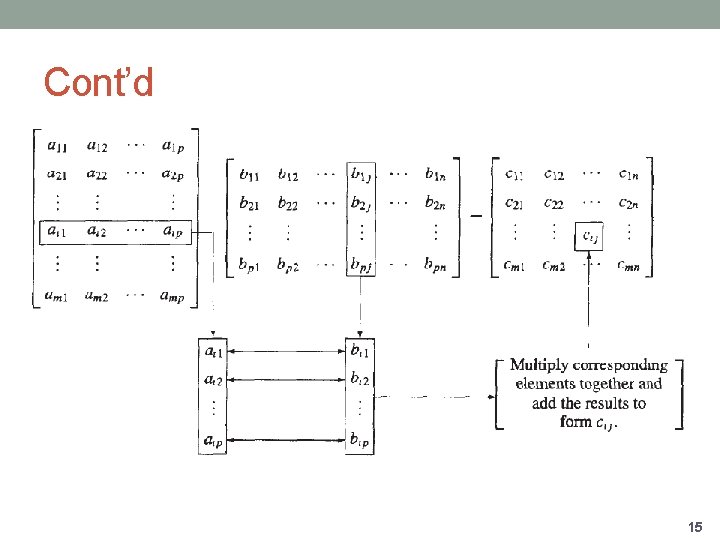
Matrices Production DEFINITION 4: Let A be an m x k matrix and B be a k x n matrix. The product of A and B, denoted by AB, is the m x n matrix with its ( i, j )th entry equal to the sum of the products of the corresponding elements from the I th row of A and the j th column of B. In other words, if AB = [cij], then cij = ai 1 b 1 j + ai 2 b 2 j + … + aik bkj. • The product of the two matrices is not defined when the number of columns in the first matrix and the number of rows in the second matrix is not the same. NOTE: Matrix multiplication is not commutative! 14

Cont’d 15

Cont’d • Example: Let A = and B = 3× 2 4× 3 Find AB if it is defined. AB = 4× 2 16

Cont’d • Example: 2× 3 3× 4 2× 4 17

Matrices • If A and B are two matrices, it is not necessarily true that AB and BA are the same. • E. g. if A is 2 x 3 and B is 3 x 4, then AB is defined and is 2 x 4, but BA is not defined. • Even when A and B are both n x n matrices, AB and BA are not necessarily equal. • Example: Let A 2 x 2 = and B 2 x 2= Does AB = BA? Solution: AB = and BA = 18

Properties of Multiplication • If A = m x p matrix, and B is a p x n matrix, then AB can be computed and is an m x n matrix. • As for BA, we have four different possibilities: 1. BA may not be defined; we may have n ≠ m 2. BA may be defined if n = m, and then BA is p x p, while AB is m x m and p ≠ m. Thus AB and BA are not equal 3. AB and BA may both the same size, but not equal as matrices AB ≠ BA 4. AB = BA 19

Basic Properties of Multiplication • The basic properties of matrix multiplication are given by the following theorem: 1. A(BC) = (AB)C 2. A(B + C)= AB + AC 3. (A + B)C = AC + BC 20

Identity Matrix • The n×n diagonal matrix all of whose diagonal elements are 1 and 0’s everywhere else, is called the identity matrix of order n, denoted by In. • A In = A • Multiplying a matrix by an appropriately sized identity matrix does not change this matrix. • In other words, when A is an m x n matrix, we have v A In = Im A = A 21

Powers of Matrices • Powers of square matrices can be defined. • If A is an n n square matrix and p 0, we have Ap AAA ··· A p times • A 0 nxn = In square matrix to the zero power is identity matrix. • Example: 22

Powers of Matrices cont. • If p and q are nonnegative integers, we can prove the following laws of exponents for matrices: • Ap Aq = Ap+q • (Ap)q =Apq • Observe that the rule (AB)p =Ap. Bp does not hold for square matrices unless AB = BA. • If AB = BA, then (AB)p =Ap. Bp. 23

Transpose Matrices DEFINITION 6: Let A = [aij] be an m x n matrix. The transpose of A, denoted by At, is the n x m matrix obtained by interchanging the rows and columns of A. In other words, if At = [bij], then bij = aji, for i = 1, 2, …, n and j = 1, 2, …, m. • Example: The transpose of the matrix is the matrix • Example 2: • Let , Find At. 24

Properties for Transpose • If A and B are matrices, then 25

Symmetric Matrices DEFINITION 7: A square matrix A is called symmetric if A = At. Thus A = [aij] is symmetric if aij = aji for all i and j with 1 <= i <= n and 1 <= j <= n. • Example: The matrix is symmetric. • Example: 26

Symmetric Matrices • Which is symmetric? A B C 27

Boolean Matrix Operation A matrix with entries that are either 0 or 1 is called a Boolean matrix or zero-one matrix. • 0 and 1 representing False & True respectively. Example: 1 0 0 1 1 1 0 • The operations on zero-one matrices is based on the Boolean operations v and ^, which operate on pair of bits. 28

Boolean Matrix Operations- OR • Let A = [aij] and B = [bij] be m x n Boolean matrices. 1. We define A v B = C = [ Cij], the join of A and B, by 1 if aij = 1 or bij = 1 Cij = 0 if aij and bij are both 0 29

Example • Find the join of A and B: A= 1 0 1 0 B= 0 1 1 0 The join between A and B is A B = =1 v 0 0 v 1 1 v 0 = 0 v 1 1 v 1 0 v 0 1 1 1 0 30

Boolean Matrix Operations- Meet • We define A ^ B = C = [ Cij], the meet of A and B, by 1 Cij = 0 if aij and bij are both 1 if aij = 0 or bij = 0 • Meet & Join are the same as the addition procedure üEach element with the corresponding element in the other matrix üMatrices have the same size 31

Example Find the meet of A and B: A= 1 0 1 0 Av. B= 1^0 0^1 B= 0 1 1 0 0^1 1^0 0^0 = 0 0 1 0 32

Boolean PRODUCT • The Boolean product of A and B, denoted, A⊙B is the m x n Boolean matrix defined by: Cij 1 if aik = 1 and bkj = 1 for some k, 1 ≤ k ≤ p 0 otherwise • The Boolean product of A and B is like normal matrix product, but using instead + and using instead . Procedure: • Select row i of A and column j of B, and arrange them side by side • Compare corresponding entries. If even a single pair of corresponding entries consists of two 1’s, then Cij = 1, otherwise Cij = 0 33

Example Find the Boolean product of A and B: A 3 x 2= 1 0 B 2 x 3 = 1 1 0 0 1 1 1 0 A⊙B 3 x 3 = (1 ^ 1) v (0 ^ 0) (0 ^ 1) v (1 ^ 0) (1 ^ 1) v (0 ^ 1) v (1 ^ 1) v (0 ^ 1) (1 ^ 0) v (0 ^ 1) (0 ^ 0) v (1 ^ 1) (1 ^ 0) v (0 ^ 1) 1 1 0 = 0 1 1 0 34

Boolean Operations Properties • If A, B, and C are Boolean Matrices with the same sizes, then a. A v B = B v A b. A ^ B = B ^ A c. (A v B) v C = A (B v C) d. (A ^ B) ^ C = A ^ (B ^ C) 35

Boolean Powers • For a square zero-one matrix A, and any k 0, the kth Boolean power of A is simply the Boolean product of k copies of A. A[k] A⊙A⊙…⊙A k times 36

Example • Find A [n]for all positive integers n. • Solution: We find that We also find that : Additional computation shows that We can notice that A [n] = A [5] for all positive integers n with n ≥ 5 37

Any Question • Refer to chapter 3 of the book for further reading