MATRICES Matrices Las matrices son arreglos compuestos por









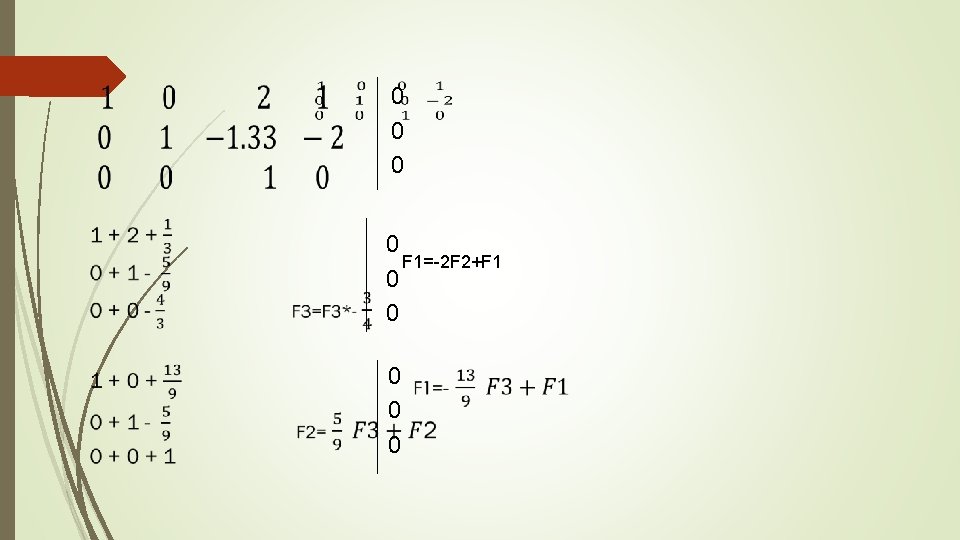









![Ejemplo: Calcule |B| si B = |B| = 2*2 -[(-1)*3] |B| = 4+3 |B| Ejemplo: Calcule |B| si B = |B| = 2*2 -[(-1)*3] |B| = 4+3 |B|](https://slidetodoc.com/presentation_image_h2/2f91ed8af20e4288d2ee6e23b2432086/image-32.jpg)



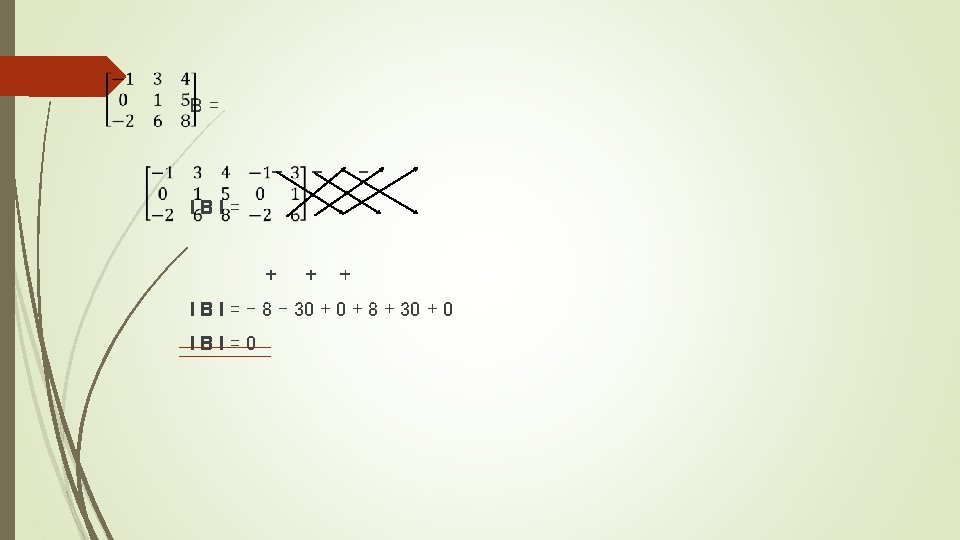

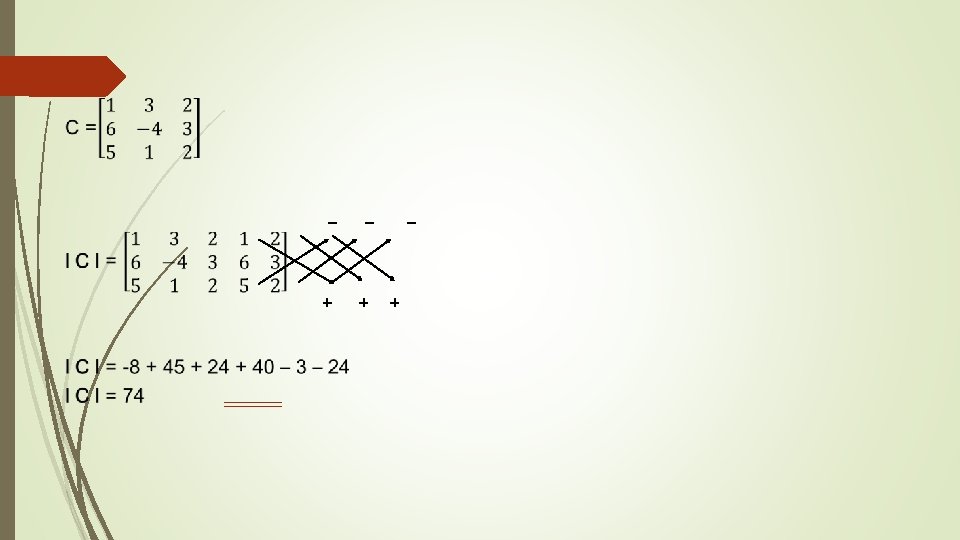





























- Slides: 87

MATRICES

Matrices Las matrices son arreglos compuestos por filas y columnas las cuales pueden contener elementos numéricos o alfabéticos. Operaciones Elementales de Matrices Para realizar operaciones de sumas o restas con matrices es necesario que tengan las mismas dimensiones, por ejemplo: § Si se va a sumar una matriz A, A 2*3 (2 filas y 3 columnas) con una B, esta deberá poner también 2 filas y 3 columnas

Ejemplos: Si -4 A= 4 6 5 B= 5 1) 3 A – B 2) B – 2 A 3) A–D 4) D–A 5) C+A -3 & 1 -7 3 A = 12 15 + ( -B) = -5 3 -1 7 = 2 -1 0 1 D= 3 A + ( - B) -12 18 1) 5 C= 1 0 2 -17 21 11 22

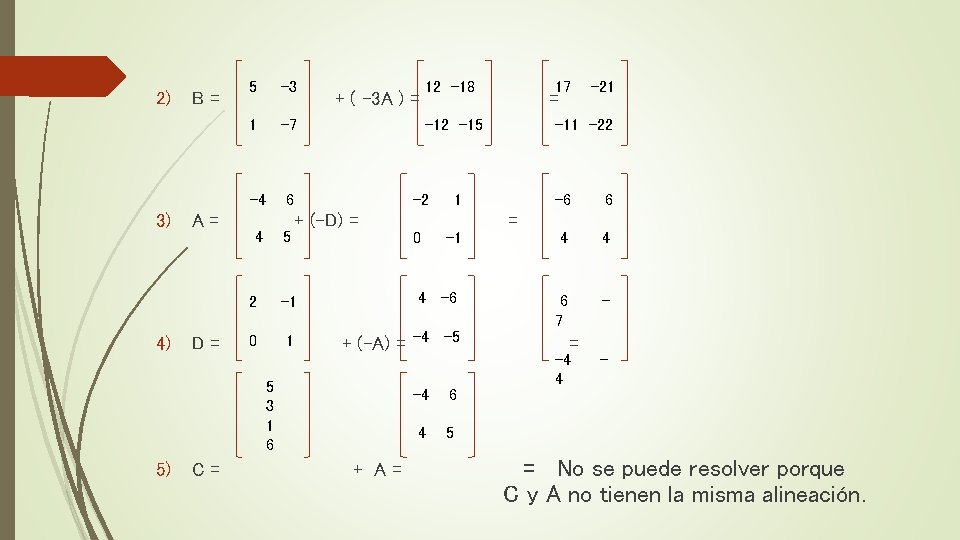
2) 3) 4) B= A= D= 5 -3 1 -7 -4 6 4 5 + ( -3 A ) = C= 17 = -12 -15 -2 + (-D) = 0 -1 -1 4 -6 0 1 + (-A) = -4 -5 + A= -4 6 4 5 -21 -11 -22 1 2 5 3 1 6 5) 12 -18 = -6 6 4 4 6 7 - = -4 4 - = No se puede resolver porque C y A no tienen la misma alineación.

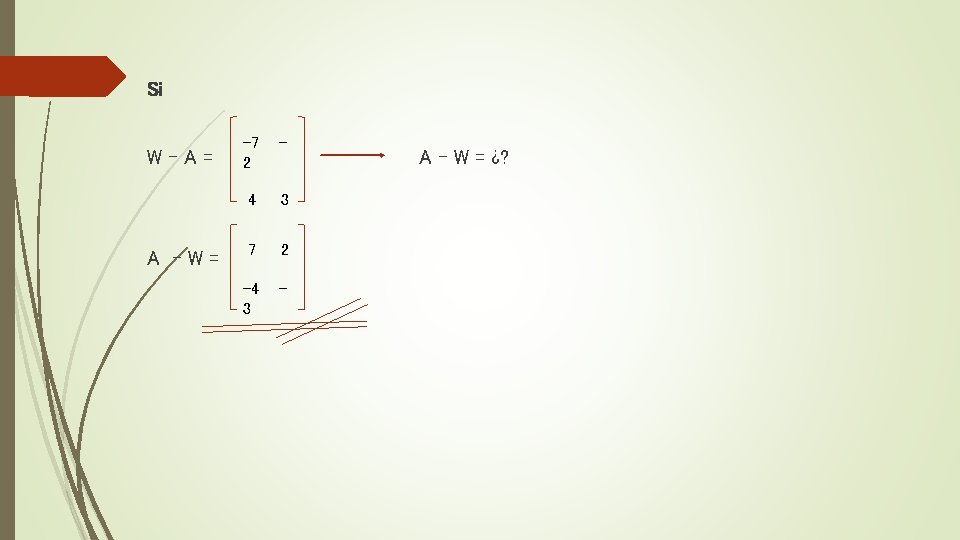
Si W-A= A -W= -7 2 - 4 3 7 2 -4 3 - A – W = ¿?

Multiplicación de Matrices Para multiplicar dos matrices debe tomarse en cuenta las siguientes propiedades si la multiplicación es a * b debe considerarse que la misma cantidad de columnas de la matriz sea igual al número de filas de la matriz b. si lo anterior se cumple se puede multiplicar la matriz a por b. Ejemplos: A 2*3 = 3 2 8 5 9 4 B 3*2 = 2 5 3 9 3 2

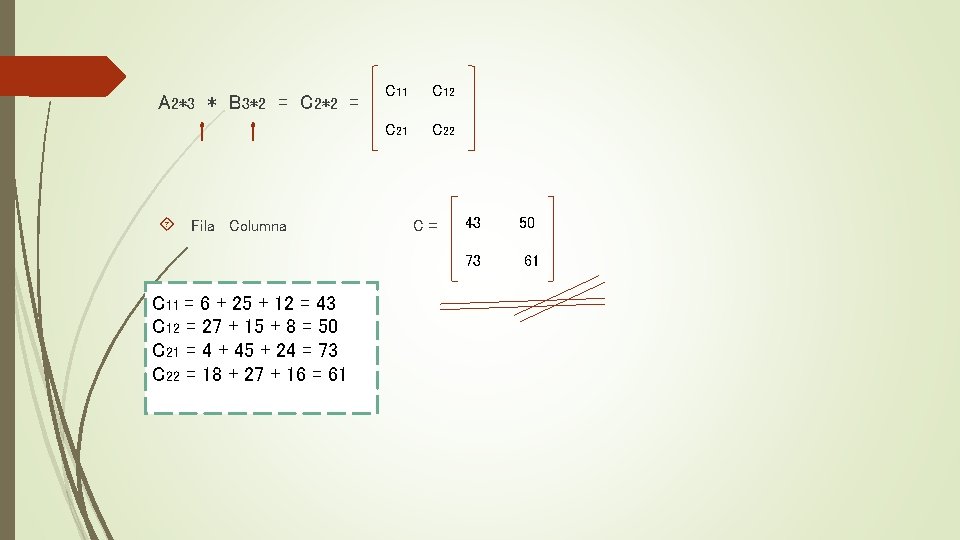
A 2*3 * B 3*2 = C 2*2 = Fila Columna C 11 C 12 C 21 C 22 C= 43 73 C 11 = 6 + 25 + 12 = 43 C 12 = 27 + 15 + 8 = 50 C 21 = 4 + 45 + 24 = 73 C 22 = 18 + 27 + 16 = 61 50 61

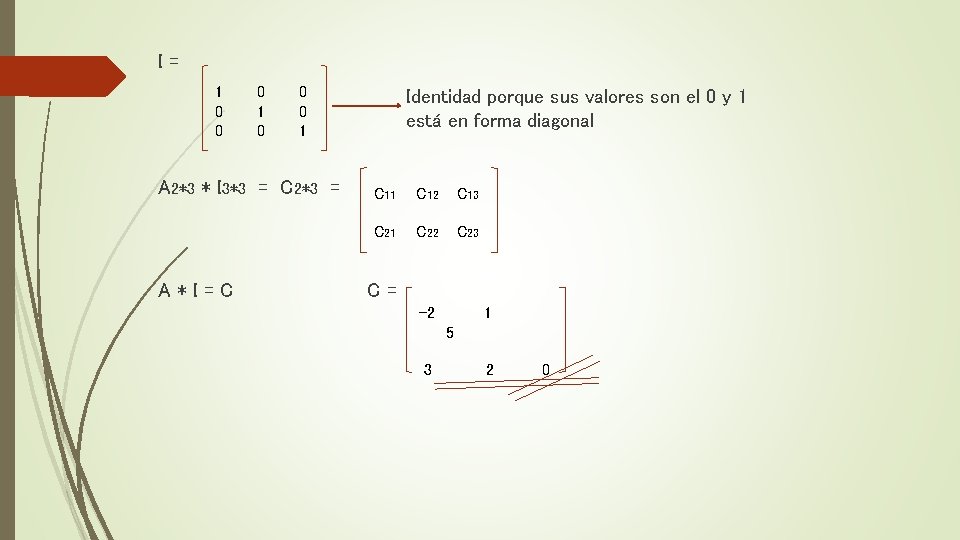
I= 1 0 0 0 1 A 2*3 * I 3*3 = C 2*3 = A*I=C Identidad porque sus valores son el 0 y 1 está en forma diagonal C 11 C 12 C 13 C 21 C 22 C 23 C= -2 1 5 3 2 0

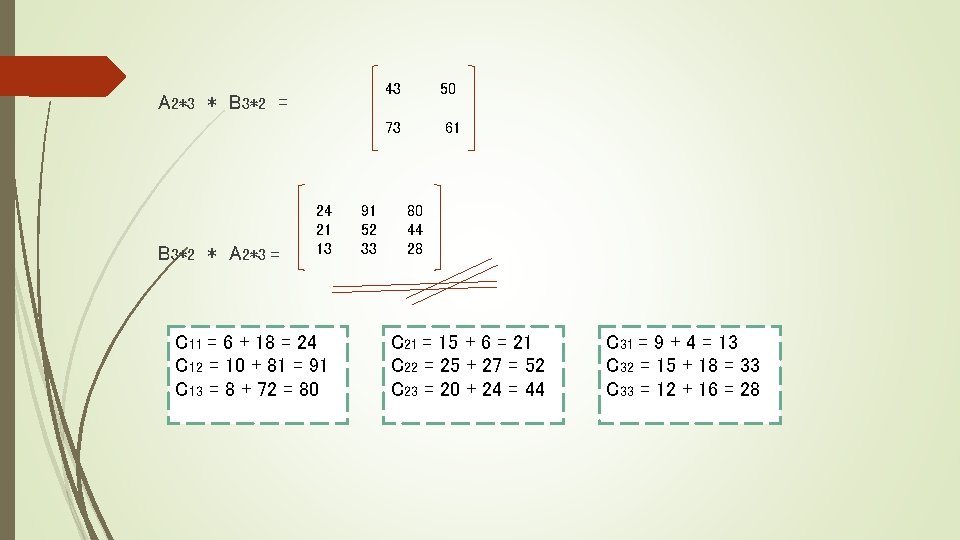
43 A 2*3 * B 3*2 = 50 73 B 3*2 * A 2*3 = 24 21 13 C 11 = 6 + 18 = 24 C 12 = 10 + 81 = 91 C 13 = 8 + 72 = 80 91 52 33 61 80 44 28 C 21 = 15 + 6 = 21 C 22 = 25 + 27 = 52 C 23 = 20 + 24 = 44 C 31 = 9 + 4 = 13 C 32 = 15 + 18 = 33 C 33 = 12 + 16 = 28

SISTEMA DE ECUACIONES LINEALES

RESOLUCIÓN DE SISTEMAS LINEALES 1. Método de Gauss Jordan: reducción de filas y columnas, sustitución hacía atrás. Fila intercambiada una con otra sin cambiar el valor de las variables. Fila multiplicada por cualquier numero diferente a cero. Sumar filas entre si o restar. Si se reduce a cero elementos de la columna uno, la fila pivote será la fila uno y si es la dos la fila pivote será la dos y así sucesivamente.

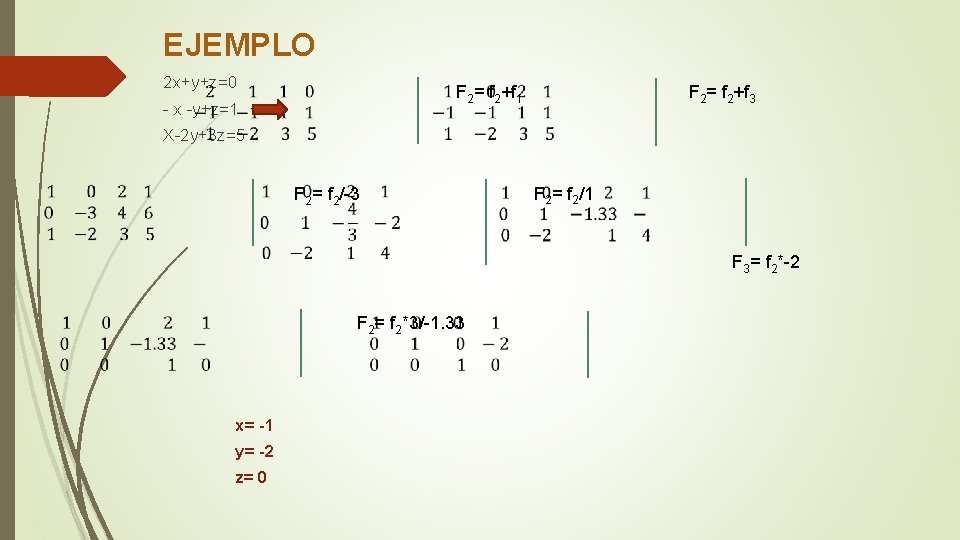
EJEMPLO 2 x+y+z=0 F 2= f 2+f 3 F 2= f 2+f 1 - x -y+z=1 X-2 y+3 z=5 F 2= f 2/-3 F 2= f 2/1 F 3= f 2*-2 F 2= f 2*3/-1. 33 x= -1 y= -2 z= 0

METODO DE KRAMMER Se utilizan solo variables. Primero se saca la determinante de la matriz sin tomar en cuenta la matriz ampliada ósea los números que están después del signo igual esos no se tomas para sacar la determinante original. Segundo la primer columna se cambia por la columna ampliada y se procede a sacar la determinante. Tercero se cambia la segunda columna por la columna ampliada y se saca la determinante. Cuarto se cambia la tercera columna por la columna ampliada y se saca la determinante. Quinto cada resultado de las determinantes se divide dentro del resultado de la determinante original. Y de esta manera obtenemos nuestros resultados. EJEMPLO:

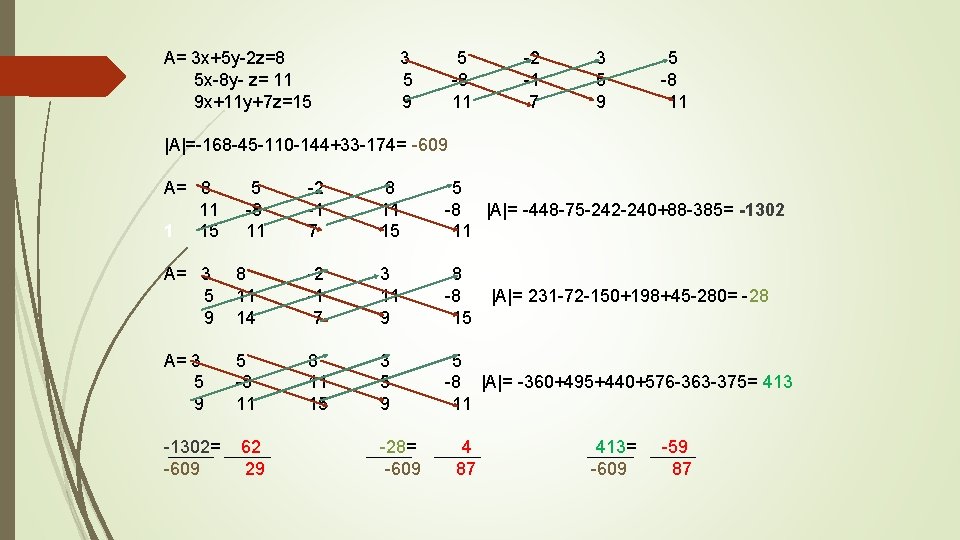
A= 3 x+5 y-2 z=8 5 x-8 y- z= 11 9 x+11 y+7 z=15 3 5 9 5 -8 11 -2 -1 7 3 5 9 5 -8 11 |A|=-168 -45 -110 -144+33 -174= -609 A= 8 11 1 15 5 -8 11 -2 -1 7 8 11 15 5 -8 |A|= -448 -75 -242 -240+88 -385= -1302 11 A= 3 5 9 8 11 14 -2 -1 7 3 11 9 8 -8 15 A= 3 5 9 5 -8 11 15 3 5 9 5 -8 |A|= -360+495+440+576 -363 -375= 413 11 -1302= -609 62 29 -28= -609 4 87 |A|= 231 -72 -150+198+45 -280= -28 413= -609 -59 87

Sistema Homogéneo

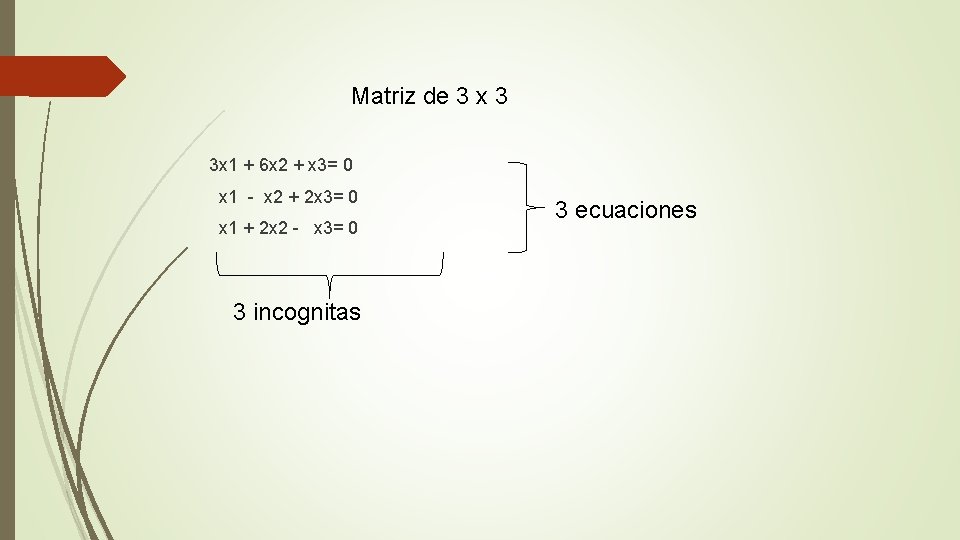
Matriz de 3 x 3 3 x 1 + 6 x 2 + x 3= 0 x 1 - x 2 + 2 x 3= 0 x 1 + 2 x 2 - x 3= 0 3 incognitas 3 ecuaciones

Determinar el Vector para el Siguiente Sistema 3+6+1 1 - 1+2 - 1 0 0 0 F 2=-F 1+F 2 F 3=-F 1+F 3
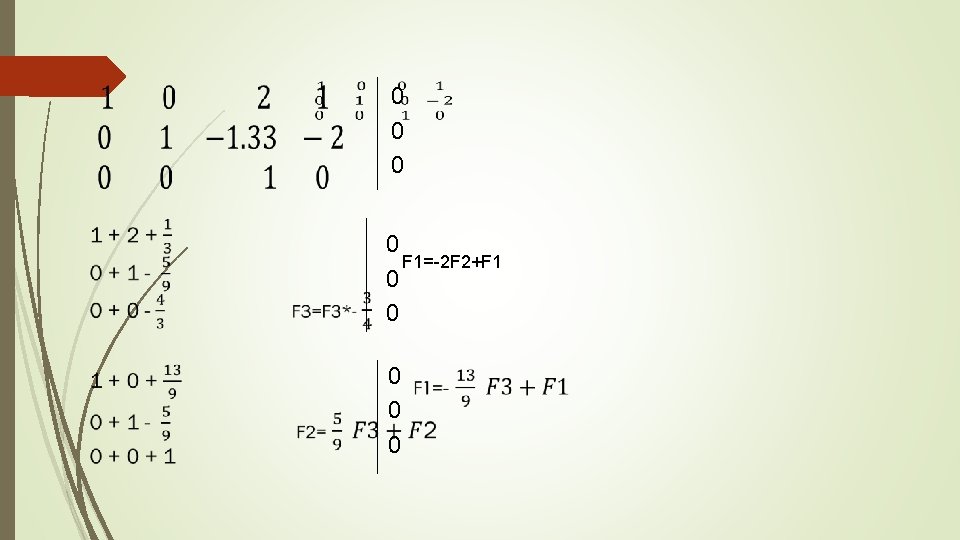
0 0 F 1=-2 F 2+F 1 0 0 0

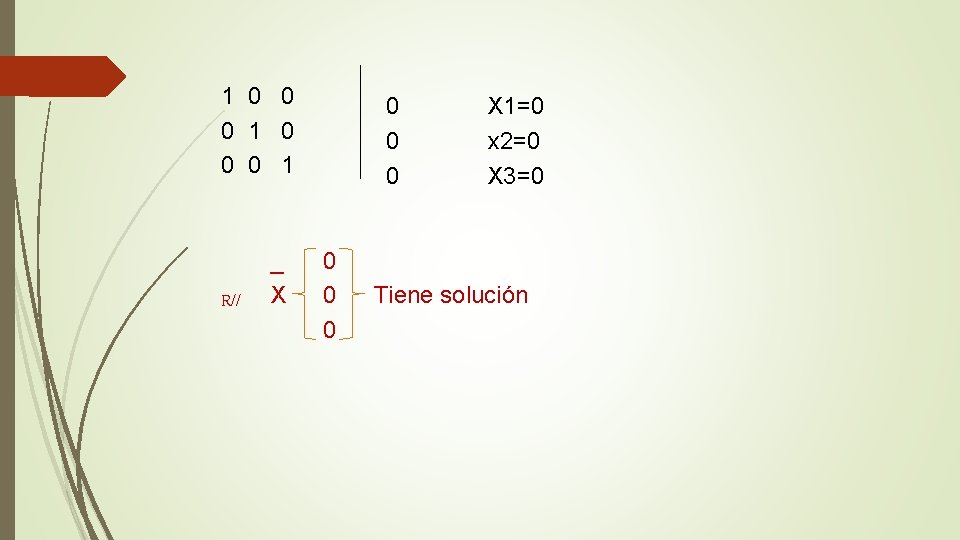
1 0 0 0 1 R// _ X 0 0 0 X 1=0 x 2=0 X 3=0 Tiene solución

Traspuesta de una Matriz

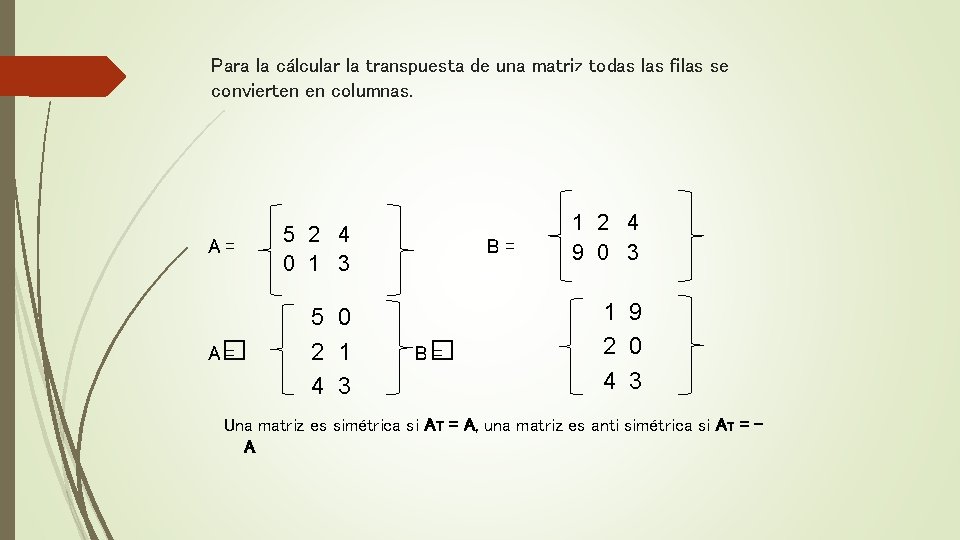
Para la cálcular la transpuesta de una matriz todas las filas se convierten en columnas. A= A� = 5 2 4 0 1 3 5 0 2 1 4 3 B= B� = 1 2 4 9 0 3 1 9 2 0 4 3 Una matriz es simétrica si AT = A, una matriz es anti simétrica si AT = A

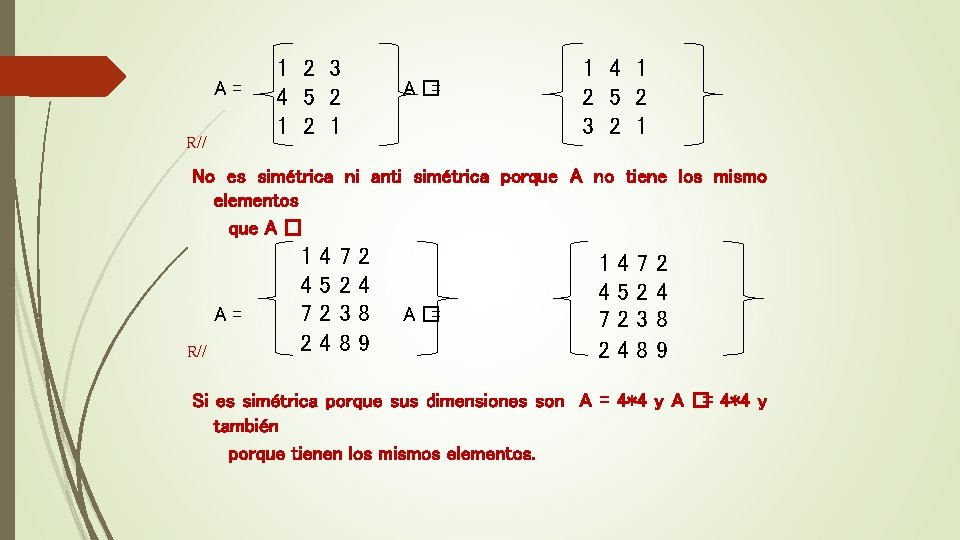
3 4 1 A= R// A� = -1 5 2 3 -1 4 5 1 2 No es simétrica ni anti simétrica porque sus dimensiones no son iguales, A = 2*3 no es igual a A � = 3*2 A= 3 2 A� = 3 2 2 3 R// Si es simétrica porque sus dimensiones son A = 2*2 y A �= 2*2 y también porque tienen los mismos elementos. A= 3 4 1 4 5 2 1 A� = 3 4 1 4 5 2 1 R// Si es simétrica porque sus dimensiones son A = 3*3 y A �= 3*3 y también porque tienen los mismos elementos.

A= R// 1 2 3 4 5 2 1 A� = 1 4 1 2 5 2 3 2 1 No es simétrica ni anti simétrica porque A no tiene los mismo elementos que A � A= R// 1 4 7 2 4 5 2 4 7 2 3 8 2 4 8 9 A� = 1 4 7 2 4 5 2 4 7 2 3 8 2 4 8 9 Si es simétrica porque sus dimensiones son A = 4*4 y A �= 4*4 y también porque tienen los mismos elementos.

Inversa de una Matriz

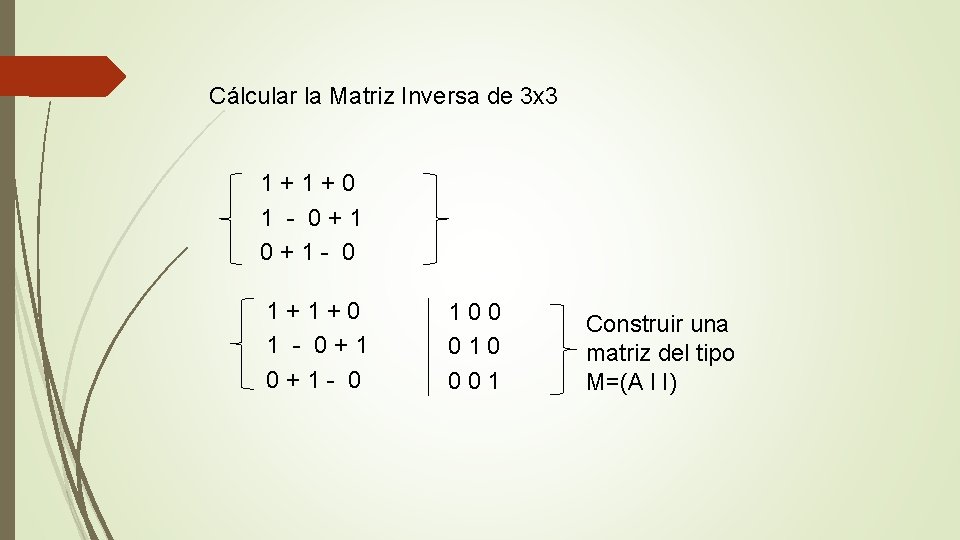
Cálcular la Matriz Inversa de 3 x 3 1+1+0 1 - 0+1 0+1 - 0 100 010 001 Construir una matriz del tipo M=(A l I)

Utilizar el método Gauss para transformar la mitad izquierda, A, en la matriz identidad, y la matriz que resulte en el lado derecho será la matriz inversa: A− 1. 1+1+0 1 - 0+1 - 0 100 010 001 1+1+0 0 - 1+1 0+0+1 100 -1 1 1 F 2=F 2 -F 1 F 3=F 3+F 2 F 2=F 2 -F 3 F 1=F 1+F 2

1+0+0 0 - 1+0 0+0+1 1 0 -1 0 0 -1 -1 1 1 1+0+0 0+1+0 0+0+1 1 0 -1 001 -1 1 1 R// F 2=(-1)F 2 1 0 -1 001 -1 1 1 Traspuesta

INVERSA, DETERMINANTES MATRICES

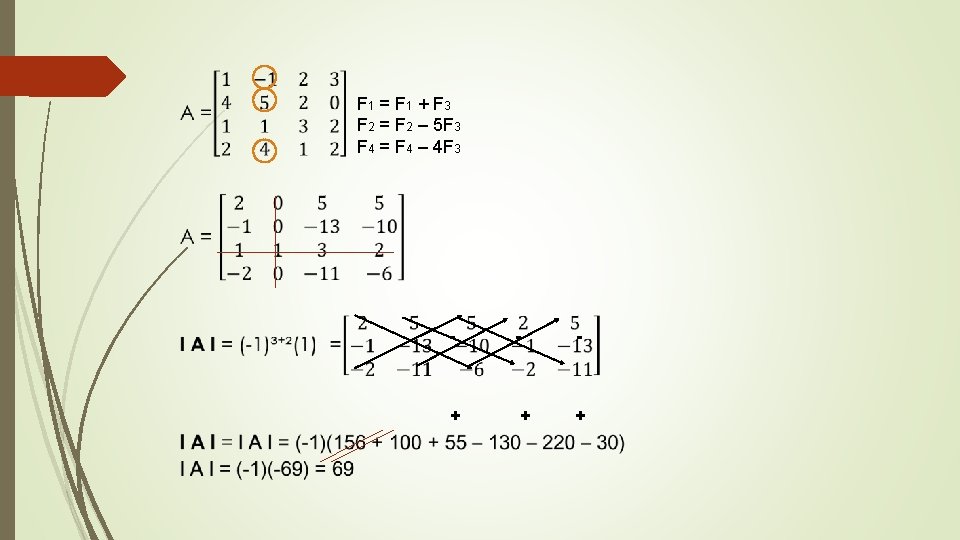
Inversa Determine la inversa, si es que existe por el método de Gauss. F 2=F 2 -F 1 F 3=f 3 -F 1 A= F 1=F 1 -3 F 3 F 1=F 1 -3 F 2 A-1=

F 1 = F 1 – 2 F 2 F 1 = 2 F 1 + F 3 F 2 = 3 F 2 - F 3 F 1 = - F 1/2 F 2 = F 2/3 F 3 = F 3/6 A⁻¹ =

Determinantes Las determinantes son valores que vienen de una matriz que servirán más adelante para el calculo de la inversa y también para la solución de sistemas lineales. Para la resolución de las determinantes existen varios métodos para su resolución que varían según la dimensión de la matriz. Determinantes (Matrices 2*2)
![Ejemplo Calcule B si B B 22 13 B 43 B Ejemplo: Calcule |B| si B = |B| = 2*2 -[(-1)*3] |B| = 4+3 |B|](https://slidetodoc.com/presentation_image_h2/2f91ed8af20e4288d2ee6e23b2432086/image-32.jpg)
Ejemplo: Calcule |B| si B = |B| = 2*2 -[(-1)*3] |B| = 4+3 |B| = 7 F 2=F 2+F 1 B= |B| = 7 F 1=F 1+F 2 |B| = 7 B=

F 2 = 4 F 1 + F 2 B= l B l = -8 B= l. Bl=8 B= C 1 + C 2 l. Bl=8 B= l. Bl=8

F 1 = 9 F 1 B= l B l = 36 – 108 = -72 F 2 = F 1 B= l B l = -3 + 3 = 0 F 2 = 2 F 1 l. Bl=0 B=

Determinantes (Matriz 3*3) “Método de Flechas” Ejemplo:
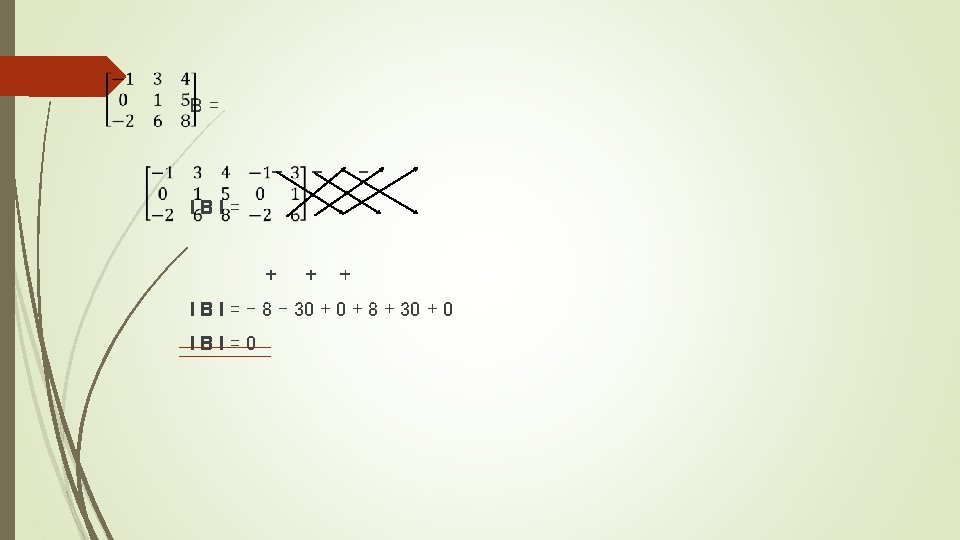

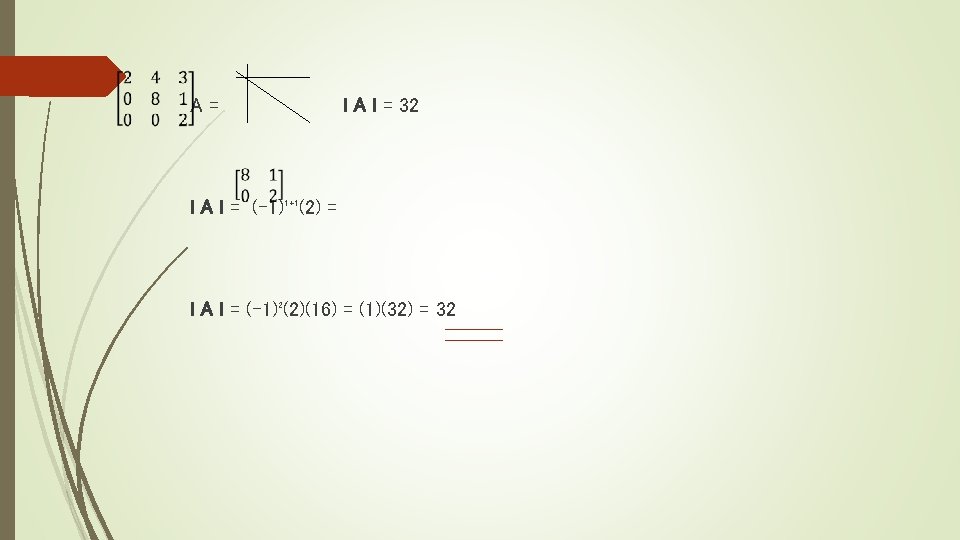
Desarrollo de Laplace (Mat. n*n) Para utilizar el método de Laplace se debe identificar la fila o la columna que más ceros tenga y esas se trabaja elemento por elemento. A= (-1)²⁺¹(1) + (-1)²⁺³(3) (-1)(4 – 5) + (-3) (-3 – 8) 1 + 33 = 34 (-1)³⁺¹(4) + (-1)³⁺²(1) (4)(6 – 0) + (-1) (-9 – 5) + (2)(0 – 2) 24 + 14 – 4 = 34 + (-1)³⁺³(2)
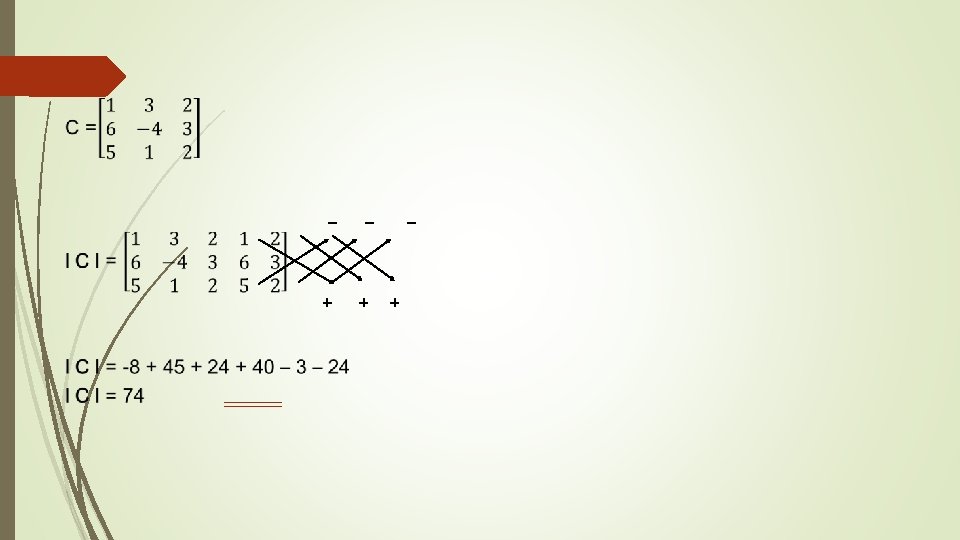



F 2 = F 2 – 4 F 1 A= F 3 – F 1 F 4 = F 4 – 2 F 1 A= A= F 3 = 3 F 3 – 2 F 2 F 4 = F 4 – 2 F 2 A= A= F 4 = 7 F 4 + F 3 = 483 / 7 = 69


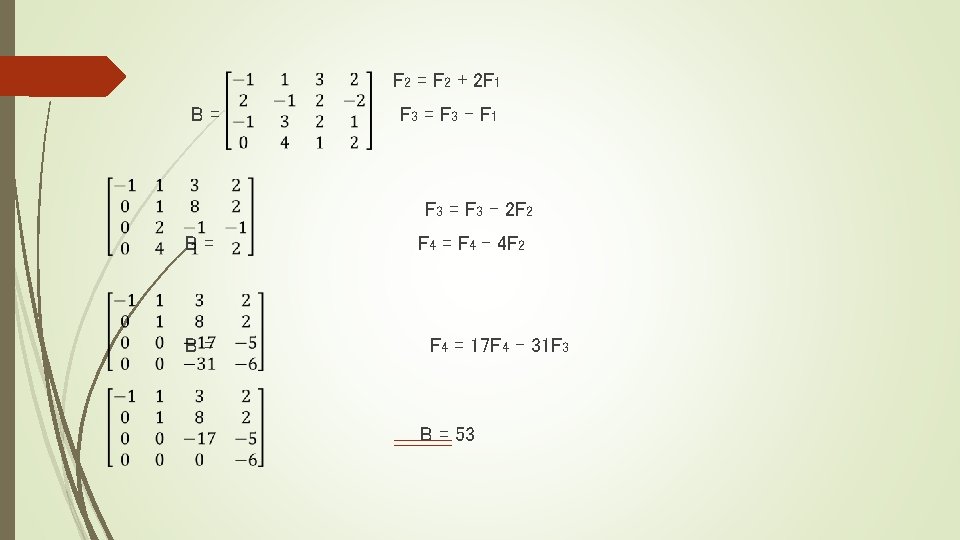
Resuelva a través del Método de Laplace la determinante. F 1 = 2 F 1 + F 2 B= F 3 = 2 F 3 + F 2 F 4 = F 4 + 0 F 2 B= - - - l B l = (-1)²⁺¹(1/2) = + + + l B l = (-1)(1/2)(12 + 0 + 10 – 48 + 0 – 80) = (-1)(1/2)(-106) = 53

F 2 = F 2 + 2 F 1 B= F 3 – F 1 F 3 = F 3 – 2 F 2 B= B= F 4 – 4 F 2 F 4 = 17 F 4 – 31 F 3 B = 53

INVERSA POR EL MÉTODO DE COFACTORES

Inversa por el Método de Cofactores Para calcular la inversa por este método se realiza atreves de la forma siguiente: Matriz A A= -1 1 2 -2 1 0 1 3 0 inversa de a = a⁻¹ = 1 ⁻¹ adj (a) l. Al adjunta de A - - -1 -2 1 -1 l A l = -2 1 1 3 1 1 +2 2 0 0+ l A l = (0 -12 + 0 -2 +0 +0) 0 l A l = - 14 - +

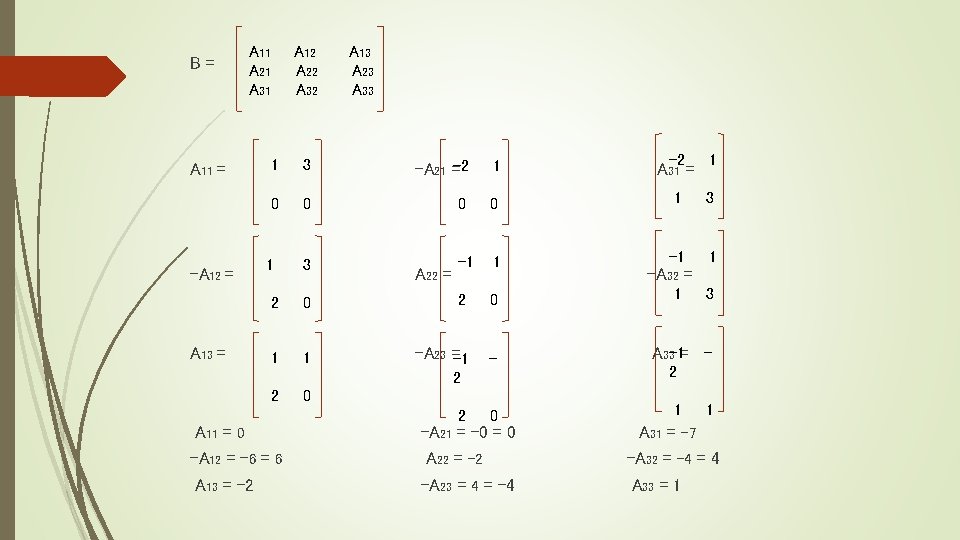
B= A 11 A 21 A 31 A 11 = -A 12 = A 13 = A 12 A 22 A 32 A 13 A 23 A 33 1 3 -A 21 =-2 1 A 31 = -2 1 0 0 1 3 3 -1 1 1 A 22 = 2 0 1 1 1 -A 23 =-1 - A 33 -1= - 0 1 2 2 0 2 A 11 = 0 -A 12 = -6 = 6 A 13 = -2 -A 32 = -A 21 = -0 = 0 A 22 = -2 -A 23 = 4 = -4 3 2 1 A 31 = -7 -A 32 = -4 = 4 A 33 = 1

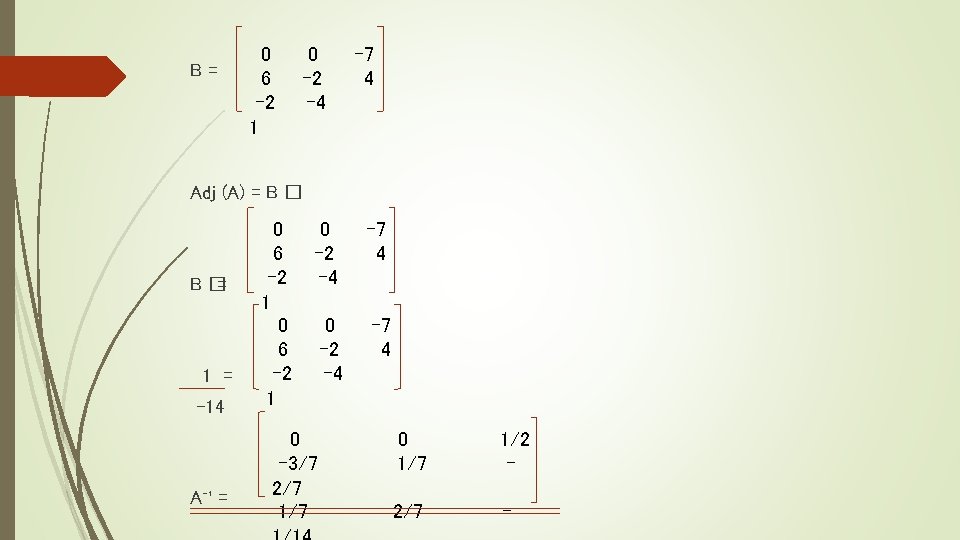
B= 0 6 -2 1 0 -2 -4 -7 4 Adj (A) = B � B� = 1 = -14 A⁻¹ = 0 6 -2 1 0 -2 -4 -7 4 0 -3/7 2/7 1/7 0 1/7 1/2 - 2/7 -

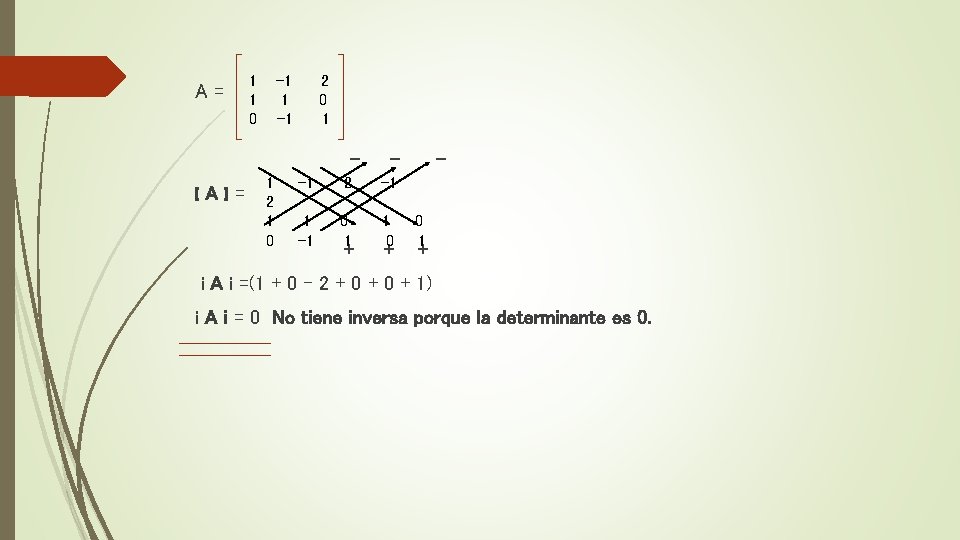
A= 1 1 0 -1 1 -1 2 0 1 IAI= 1 2 1 0 - -1 2 -1 1 -1 0 1 1 0 + + 0 1 + i A i =(1 + 0 – 2 + 0 + 1) i A i = 0 No tiene inversa porque la determinante es 0.

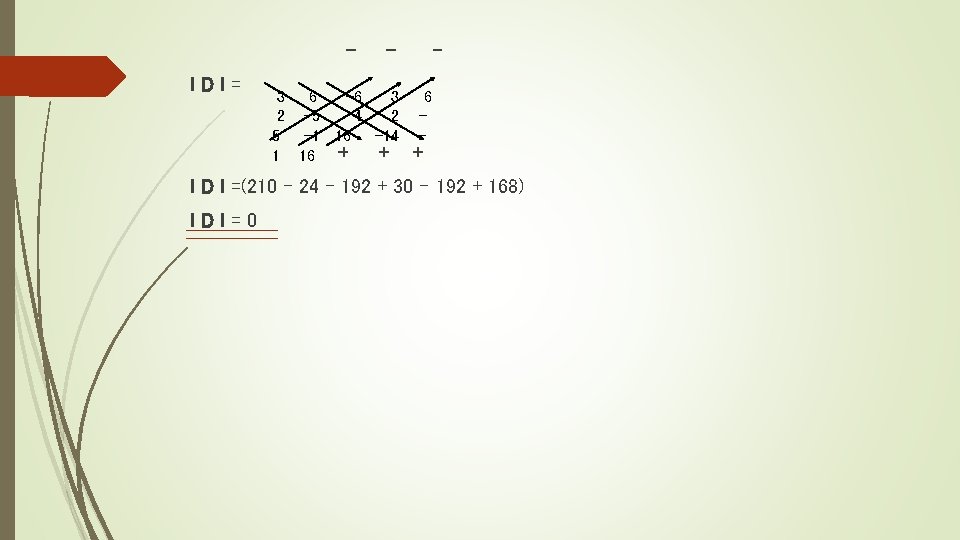
Método de Krammer Se utiliza para resolver sistemas lineales a través de determinantes. Se calcula el determinante principal a través de una matriz que contiene los elementos numéricos de los coeficientes o variables, esta determinante principal será el denominador para cada uno de los elementos del sistema. Si la determinante del sistema es cero, esto quiere decir que el sistema es trivial, ósea que tiene infinitas soluciones. 3 x 1 + 6 x 2 – 6 x 3 = 9 2 x 1 – 5 x 2 + 4 x 3 = 6 - x 1 + 16 x 2 – 14 x 3 = - 3 D= 3 2 -1 14 6 -6 -5 4 16 - Este sistema tiene infinitas soluciones porque la determinante Es cero (0)

l. Dl= - 3 6 -6 3 2 -5 4 2 5 -1 16 -14 + 1 16 + 6 - + l D l =(210 – 24 – 192 + 30 – 192 + 168) l. Dl=0

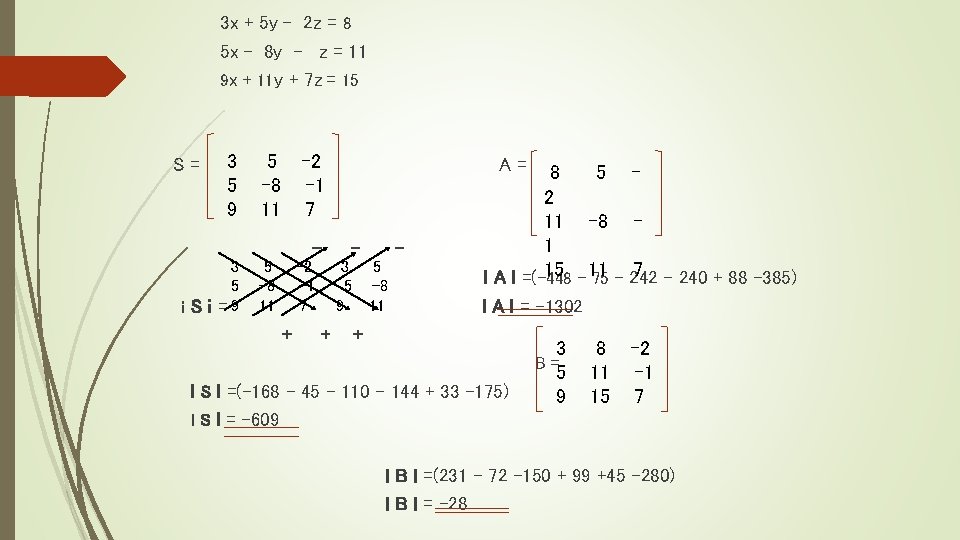
3 x + 5 y - 2 z = 8 5 x - 8 y - z = 11 9 x + 11 y + 7 z = 15 S= 3 5 9 5 -8 11 -2 -1 7 - 3 5 i S i =9 5 -8 11 -2 -1 7 + A= 3 5 9 + 5 -8 11 8 5 2 11 -8 1 7 - 240 + 88 -385) l A l =(-15 448 - 11 75 - 242 l A l = -1302 + l S l =(-168 - 45 - 110 – 144 + 33 -175) l S l = -609 3 B= 5 9 8 11 15 -2 -1 7 l B l =(231 – 72 -150 + 99 +45 -280) l B l = -28

C= 3 5 9 5 8 -8 11 11 15 l C l =(-360 + 495 + 440 + 576 – 363 - 375) l C l = 413 x = l A l = - 1302 = 434 = 62/29 l. Dl - 609 203 y = l B l = - 28 = 4/87 l. Dl - 609 87 z=l. Cl = l. Dl 413 = - 609 - 59 = -59/87 87 Sol. 69/29 , 4/87 , 59/87 x y z

PLANOS PARALELOS

Vectores en R² Definición: Es un par ordenado de números reales A y B. Los números A y B se llaman elementos o componentes del vector V. El vector 0 es el vector (0, 0). Magnitud o Longitud de un Vector: Para calcular la magnitud o longitud de un vector se eleva al cuadrado cada una de sus componentes luego se suman y se calcula su raíz cuadrada. De forma general se representa así: V=(a, b) l. Vl = Magnitud de V

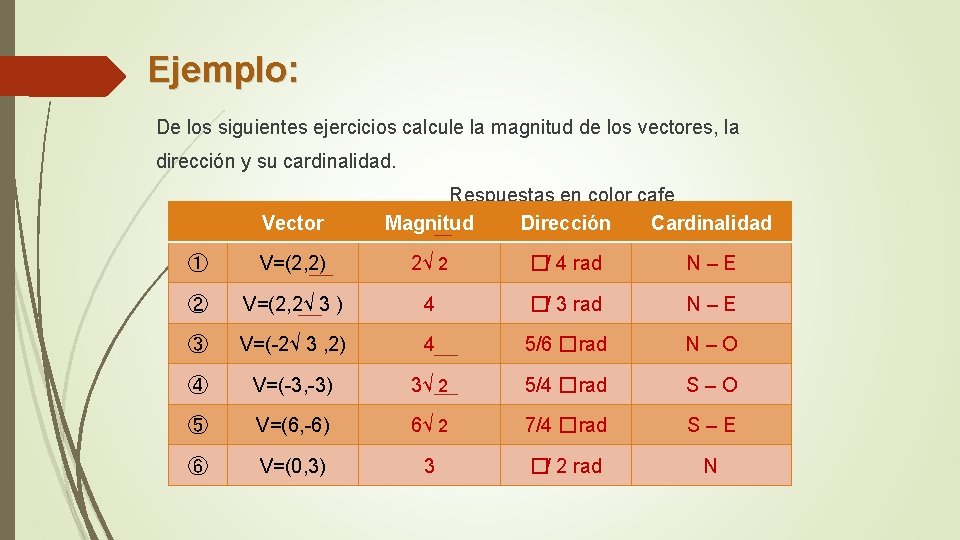
Ejemplo: De los siguientes ejercicios calcule la magnitud de los vectores, la dirección y su cardinalidad. Vector Respuestas en color cafe Magnitud Dirección Cardinalidad ① V=(2, 2) 2√ 2 �/ 4 rad N–E ② V=(2, 2√ 3 ) 4 �/ 3 rad N–E ③ V=(-2√ 3 , 2) 4 5/6 �rad N–O ④ V=(-3, -3) 3√ 2 5/4 �rad S–O ⑤ V=(6, -6) 6√ 2 7/4 �rad S–E ⑥ V=(0, 3) 3 �/ 2 rad N

Vector Unitario Un vector unitario es un vector con longitud a 1. Ejemplo: Demuestre que el vector U = ½, √ 3 / 2 es un vector unitario. �= ( ½, √ 3 / 2 ) l�l = √ (½)² + (√ 3 / 2)² l�l = √ ¼ + ¾ l�l = √ 4/4 l�l = √ 1 l�l = 1

Vectores Unitarios Asociados a Vectores Comunes Ejemplo: El vector V = ( 2 , -3 ) se puede representar así V = 2 i – 3 j. Porque i=(1, 0) j=(0, 1) & 2 i = 2 ( 1 , 0 ) = ( 2 , 0 ) -3 j = -3 ( 0 , 1 ) = ( 0 , -3 ) ( 2 , -3 ) Son unitarios

¿Cómo convertir cualquier vector a vector unitario Ejemplo: Dado el vector V = 3 i + 4 j encuentre un vector unitario que vaya en la misma dirección que V. l. V l = √ ( 3 ) ² + ( 4 ) ² l. V l = √ 25 l. V l =5 Uv = 3 i + 4 j 5 5

Vectores en el espacio R³ Los tres ejes que se trabajan en un sistema tridimensional determinan tres (3) planos coordenados que se llaman plano xy, plano xz y plano yz. El plano xy contiene los ejes x e y simplemente es el plano que se ha venido trabajando hasta ahora. Se puede pensar en los planos xz e yz es una forma similar. Teniendo en cuenta la estructura construida de los ejes coordenados y planos se puede describir cualquier punto p en l. R³ de una sola manera: P=(x, y, z)

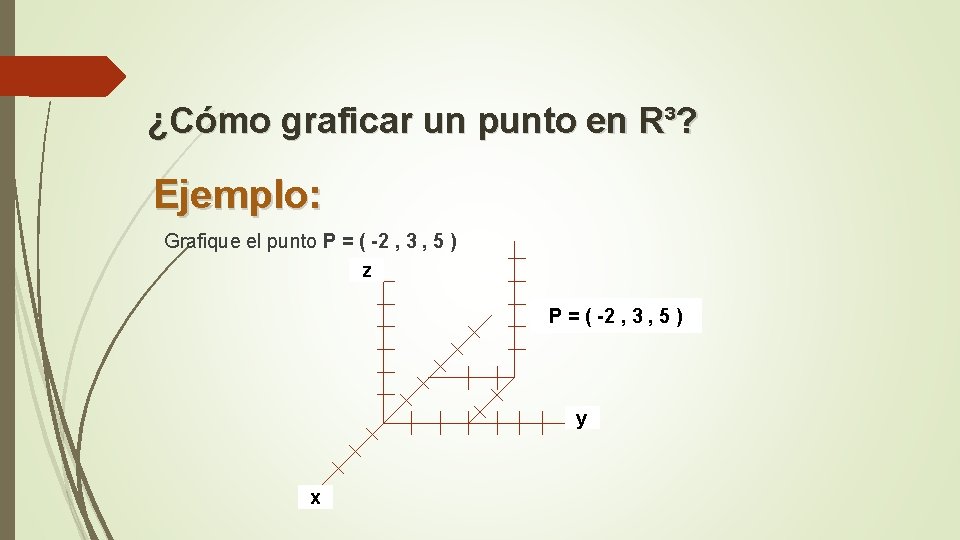
¿Cómo graficar un punto en R³? Ejemplo: Grafique el punto P = ( -2 , 3 , 5 ) z P = ( -2 , 3 , 5 ) y x

Para encontrar la distancia entre dos puntos en un plano l. R³ se hace de la siguiente forma: Sea P = ( x 1 , y 1 , z 1 ) & Q = ( x 2 , y 2 , z 2 ) PQ = √ (x 1 – x 2)² + (y 1 – y 2)² + (z 1 – z 2)² Ejemplo: Sea P = ( -1 , 0 , 3 ) & Q = ( -2 , 4 , 0 ). Calcule la distancia PQ PQ = √ (-1 – (-2))² + (0 – 4)² + (3 – 0)² PQ = √ (1)² + (– 4)² + (3)² PQ = √ 1 + 16 + 9 PQ = √ 26 ≅ 5. 1

Magnitud en l. R³ Para calcular la magnitud de un l. R³ se hace exactamente igual que un l. R²; esto quiere decir que se eleva al cuadrado cada elemento del vector, se suma y se extrae raíz cuadrada. Ejemplo: Sea V = ( 1 , 3 , -2 ) l. Vl = √ (1)² + (3)² + (-2)² l. V l = √ 1 + 9 + 4 l. Vl = √ 14

Vector Unitario en l. R³ Ejemplo: Encuentre el vector unitario para V = ( 1 , 3 , -2 ) l. Vl = √ 14 �v= 1 , 3 , -2 √ 14 Ejemplo: Encuentre el vector unitario para V = ( 1 , 3 , -2 ) en dirección opuesta. l. Vl = √ 14 �v= -1 , -3 , √ 14 2 √ 14

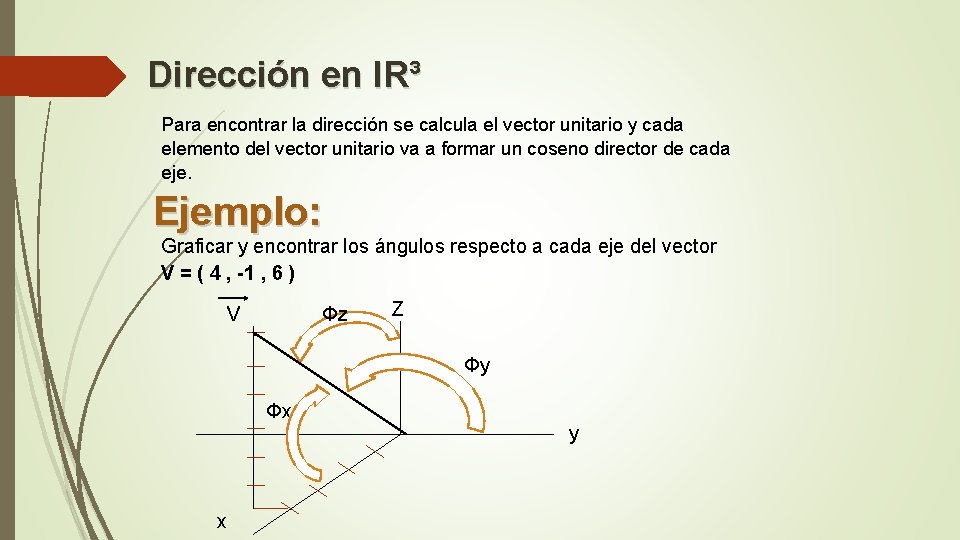
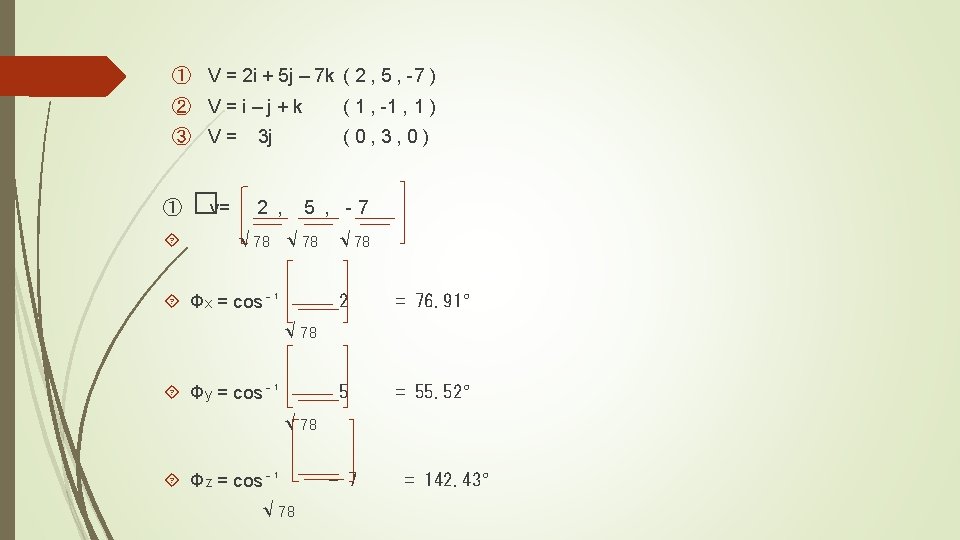
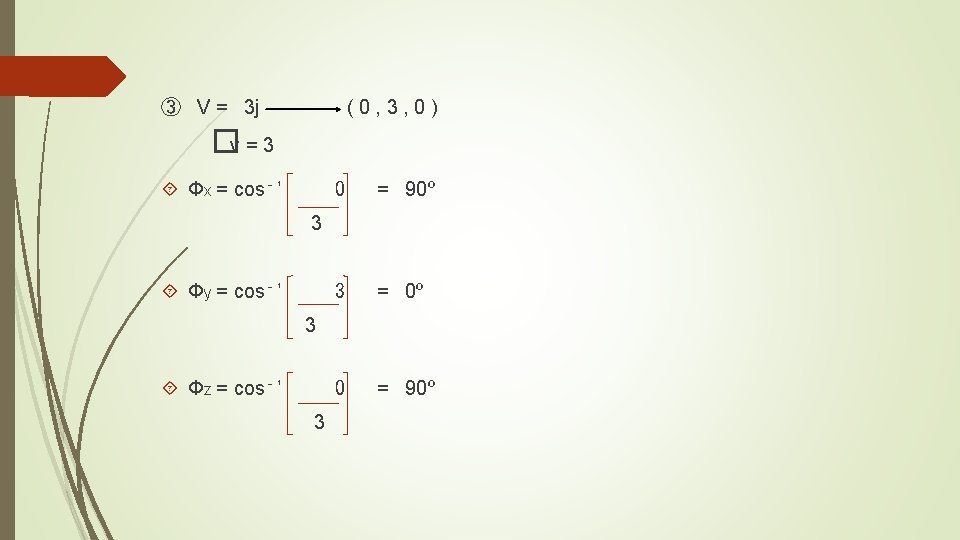
Dirección en l. R³ Para encontrar la dirección se calcula el vector unitario y cada elemento del vector unitario va a formar un coseno director de cada eje. Ejemplo: Graficar y encontrar los ángulos respecto a cada eje del vector V = ( 4 , -1 , 6 ) V Φz Z Φy Φx y x





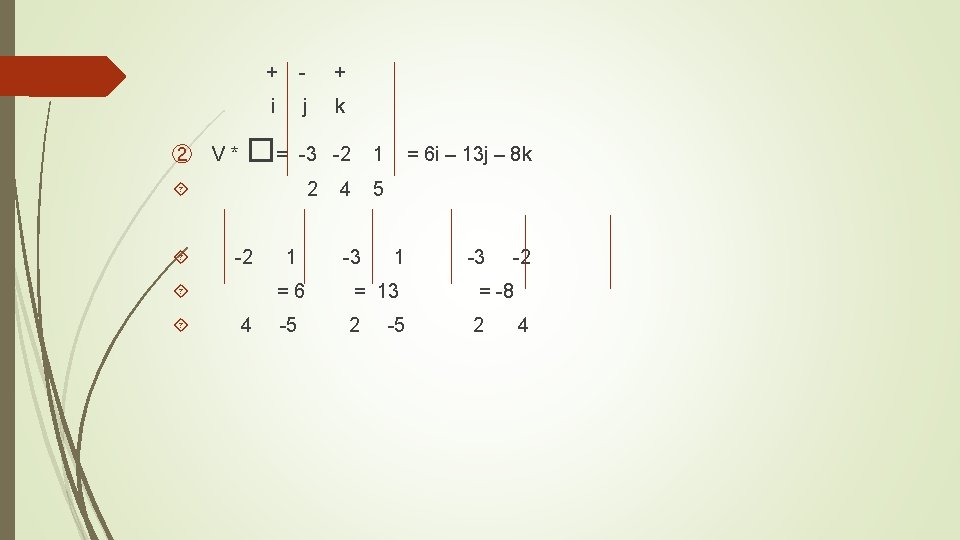
Producto Cruz de dos Vectores El producto cruz de dos vectores servirá para calcular el área de paralelogramos. Para calcular el producto cruz de dos vectores se realiza a través de una determinante entre los vectores unitarios y los vectores a los cuales se calculará el producto cruz. Ejemplo: � Calcule el producto cruz de = 2 i + 4 j – 5 k + - + V = -3 i – 2 j + k i j k ① �* V = 4 2 4 -5 -3 -2 1 -5 = -6 i + 13 j + 8 k 2 -5 = -6 -2 1 2 4 = -13 -3 1 =8 -3 -2

+ - + i j k ② V * �= -3 -2 1 5 2 -2 4 1 4 -3 = 6 i – 13 j – 8 k 1 -3 -2 =6 = 13 = -8 -5 2 2 -5 4

Aéreas de Paralelogramos en l. R³ Para calcular el área de un paralelogramo en l. R³ se grafican los puntos y luego se determinan dos vectores que conformen el paralelogramo. R Z Ejemplo: Encuentre el área del paralelogramo con vértices en: P = ( 1 , 3 , -2 ) Q=(2, 1, 4) R = ( -3 , 1 , 6 ) Q Y X P


Planos y Paralelos

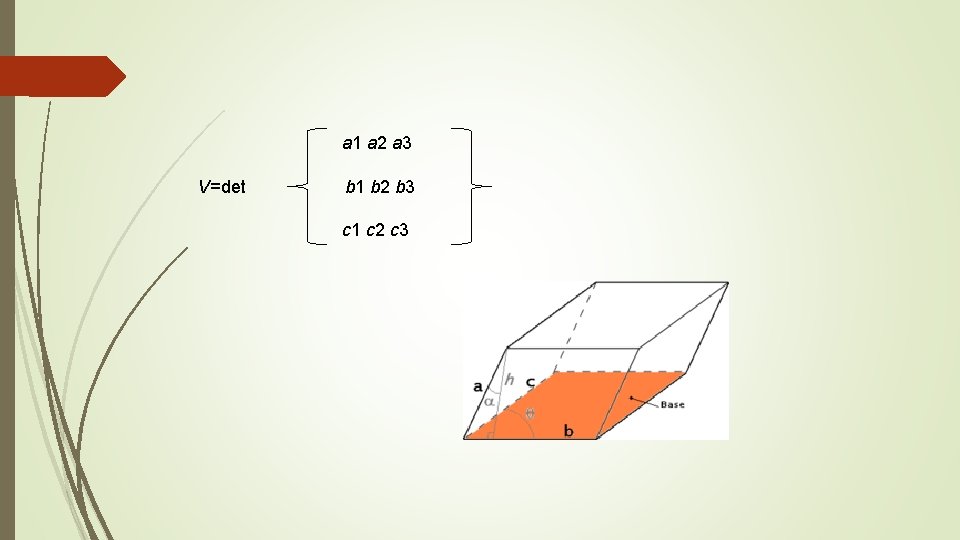
Paralelepípedo Tiene 12 aristas, que son iguales paralelas en grupos de cuatro y 8 vértices Volúme: V=A⋅h V=a⋅b⋅c V=l 3 V=|a⋅(b×c)| )|

a 1 a 2 a 3 V=det b 1 b 2 b 3 c 1 c 2 c 3

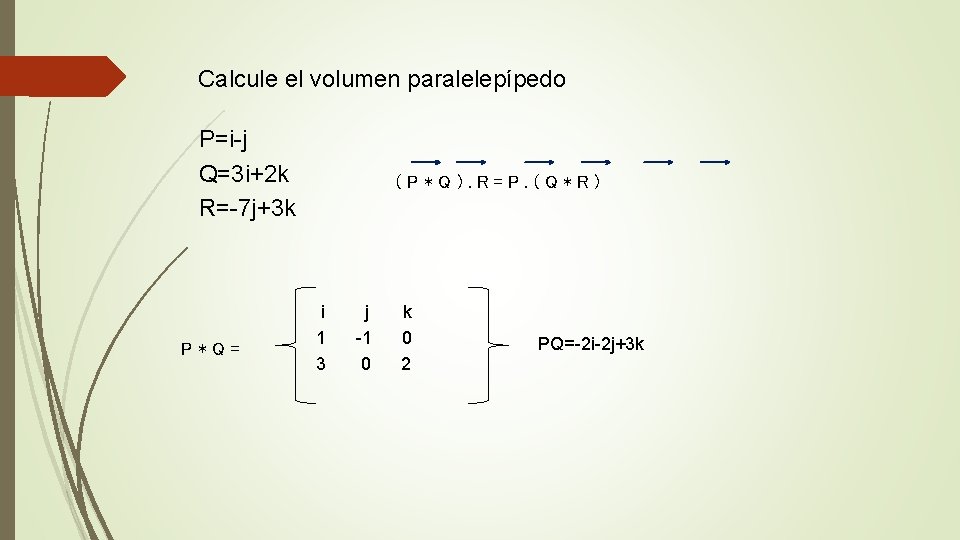
Calcule el volumen paralelepípedo P=i-j Q=3 i+2 k R=-7 j+3 k P*Q= (P*Q). R=P. (Q*R) i 1 3 j -1 0 k 0 2 PQ=-2 i-2 j+3 k

(P*Q). R=(-2 i-2 j+3 k)(0 i-7 j+3 k) volumen= 0+14+9 R// (P*Q). R=P. (Q*R)

Rectas y Planos en el Espacio

Tipos de Ecuaciones del Plano Ecuación Vectorial Expresando la ecuación 2 en coordenadas Ecuación paramétrica Separando los componentes X=x 0+ u 1+uv 1 y=y 0+ u 2+uv 2 z=z 0+ u 3+uv 3

Ecuación Simétrica x – x 1 = y – y 1 = z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x – x 1 = y – y 1 = z – z 1 a b c Encuentre la ecuación vectorial, paramétricas y simétricas P=(5, -7, 9) & Q=(-1, 5, -3) Vectorial PQ=(-1 -5)I, (5 -(-7))J, (-3 -9)K R// PQ=-6 I+12 J-12 K a b c

Por tanto: a=-6, b=12, c=-12 Parámetricas X=x 1+at y=y 1+bt z=z 1+ct X=5 -6 t y=-7+12 t z=9 -12 t R// Simétricas x – x 1 = y – y 1 = z – z 1 a b R// c x– 5 = y+7 = z– 9 -6 12 -12

Planos En vector PQ. n=0 y este forma un plano en IR 3 Ecuación del Plano Dados & P = ( x 0 , y 0 , z 0 ) Q=(x, y, z) n = ai + bj + ck PQ = ( x – x 0 ) i + ( y – y 0 ) j + ( z – z 0 ) k n = ai + bj + ck PQ. n = a ( x – x 0) + b ( y – y 0) + c ( z – z 0) 0 = ax – ax 0 + by – by 0 + cz – cz 0 ax + by + cz = ax 0 + by 0+ cz 0 ax + by + cz = d

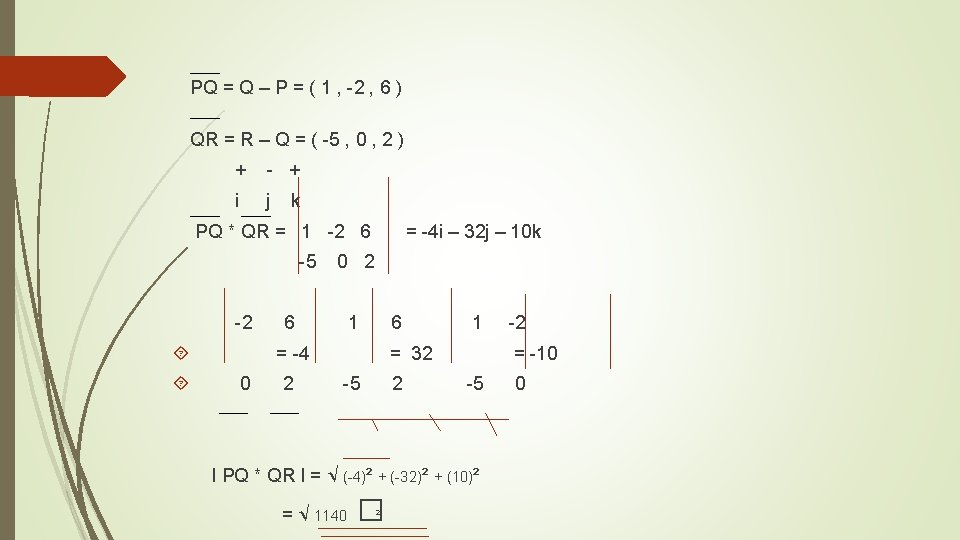
Ejercicio de Ecuación de un Plano PQ=-8, 13, 1 QR=13, -4 i j k -13 1 -8 -13 13 -4 13 13 -104 -(-109) 65 k 65(2) 130 52 -13 39 i 39(7) 273 +D=0 R// D=-251 39 x-19 y+65 z=-251 -32 -13 -19 j -19(8) -152

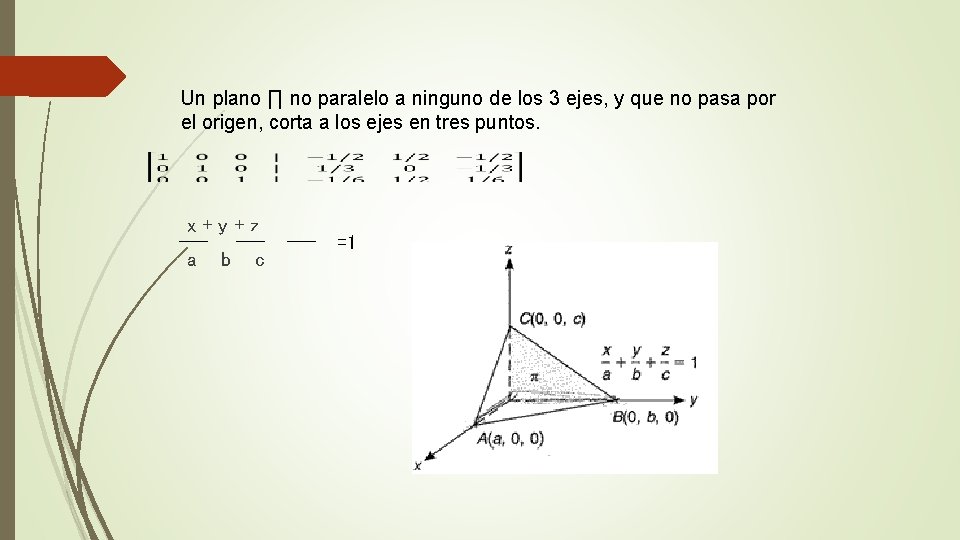
Un plano ∏ no paralelo a ninguno de los 3 ejes, y que no pasa por el origen, corta a los ejes en tres puntos. x+y+z a b c =1

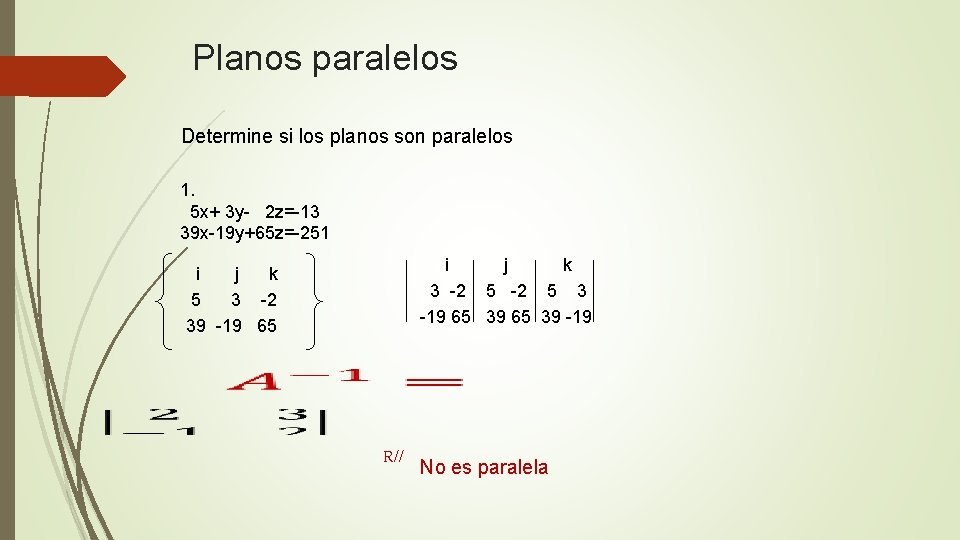
Planos paralelos Determine si los planos son paralelos 1. 5 x+ 3 y- 2 z=-13 39 x-19 y+65 z=-251 i i j k 5 3 -2 39 -19 65 j k 3 -2 5 3 -19 65 39 -19 R// No es paralela

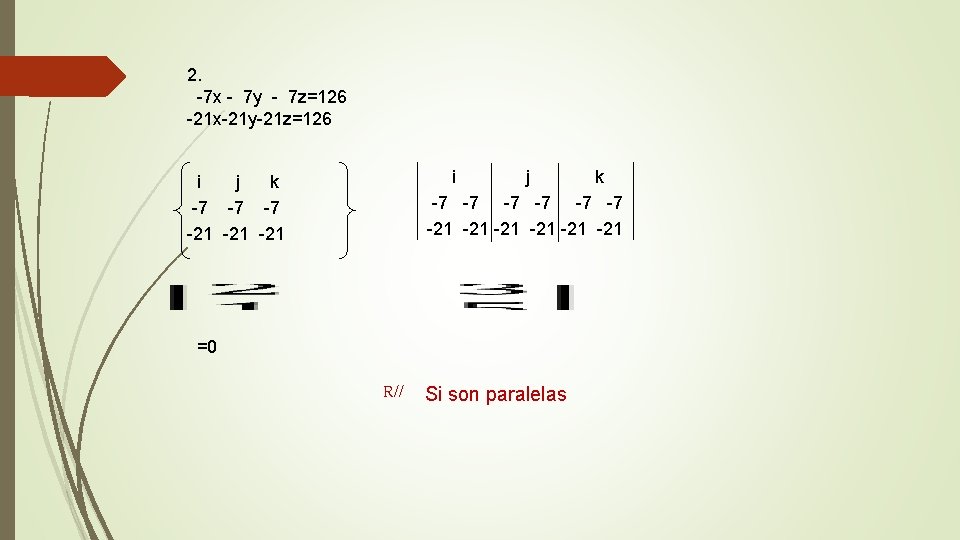
2. -7 x - 7 y - 7 z=126 -21 x-21 y-21 z=126 i i j k -7 -7 -7 -21 -21 -21 =0 R// Si son paralelas