Matrices y Determinantes Concepto de matriz Igualdad de

Matrices y Determinantes

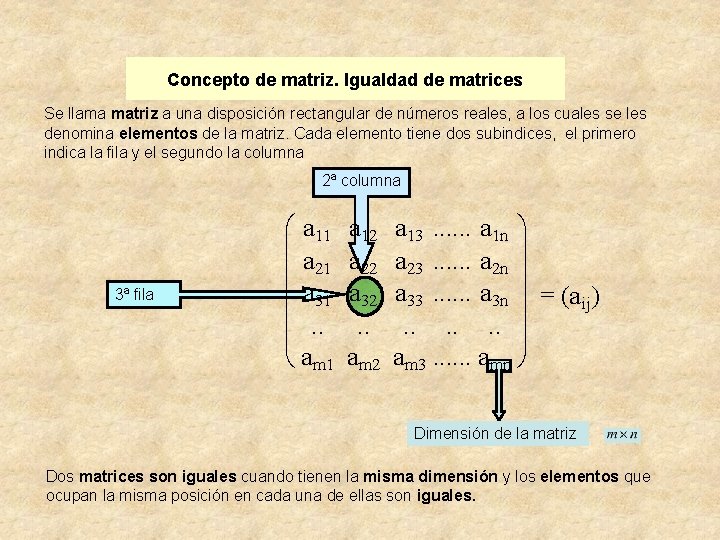
Concepto de matriz. Igualdad de matrices Se llama matriz a una disposición rectangular de números reales, a los cuales se les denomina elementos de la matriz. Cada elemento tiene dos subindices, el primero indica la fila y el segundo la columna 2ª columna 3ª fila æ a 11 ç ç a 21 ç a 31 ç. . ç è am 1 a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö ÷ a 23. . . a 2 n ÷ a 33. . . a 3 n ÷ = (aij). . . ÷÷ am 3. . . amn ø Dimensión de la matriz Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en cada una de ellas son iguales.

Definición de matríz Se llama matriz de orden m×n a todo conjunto rectangular de elementos aij dispuestos en m líneas horizontales (filas) y n verticales (columnas) de la forma: A = (ai, j)= Abreviadamente suele expresarse en la forma A =(aij), con i =1, 2, . . . , m, j =1, 2, . . . , n. Los subíndices indican la posición del elemento dentro de la matriz, el primero denota la fila ( i ) y el segundo la columna ( j ). Por ejemplo el elemento a 25 será el elemento de la fila 2 y columna 5. El orden es el número de filas y columnas que tiene la matriz, se representa por m x n.

Matriz: Ejemplo Juan, Ana y Elena han ido a una tienda y han comprado lo siguiente: 1. Juan compró dos bocadillos, un refresco y un pastel. 2. Ana se llevó un bocadillo, un refresco y un pastel. 3. Elena compró un bocadillo y un refresco. Estos datos se pueden agrupar en una matriz 2 1 1 1 1 0

Expresión matricial: ejemplo El sistema Tiene la siguiente matriz de los coeficientes: A = Tiene la siguiente matriz ampliada: A* Tiene la siguiente expresión matricial: æ ç ç è 2 5 – 3 ö÷ 1 – 4 1 ÷ø æ ç ç è 2 5 – 3 1 ö÷ = 1 – 4 1 – 2 ÷ ø æ ç ç è æ x ö æ 2 5 – 3 ç ÷ ç 1 y ÷ = çè – 2 1 – 4 1 ç è z ø ö ÷ ÷ ø

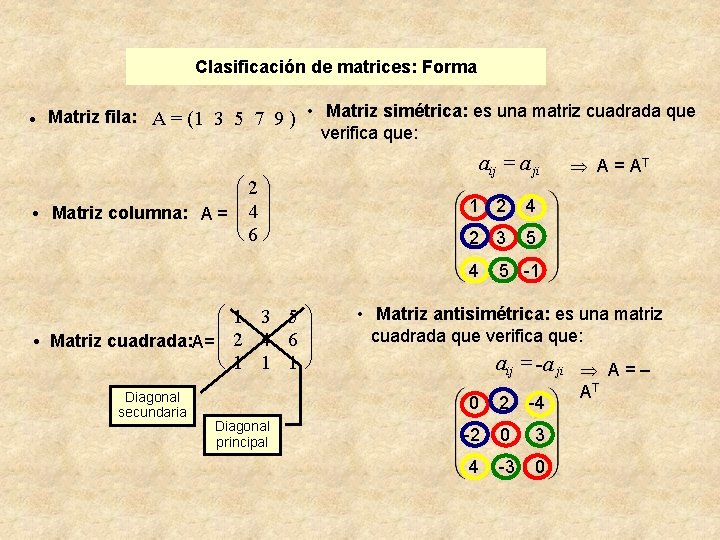
Clasificación de matrices: Forma · · Matriz fila: A = (1 3 5 7 9 ) • Matriz simétrica: es una matriz cuadrada que verifica que: aij = a ji æ 2ö ç ÷ Matriz columna: A = ç 4 ÷ è 6ø A = AT 1 2 4 2 3 5 4 5 -1 · æ 1 3 5 ç Matriz cuadrada: A= ç 2 4 6 è 1 1 1 Diagonal secundaria ö ÷ ÷ ø • Matriz antisimétrica: es una matriz cuadrada que verifica que: aij = -a ji A = – 0 2 -4 Diagonal principal -2 0 3 4 -3 0 A T

Clasificación de matrices: Elementos • Matriz nula: es una matriz en la que todos los elementos son nulos. • Matriz unidad o identidad: es una matriz escalar, cuya diagonal principal es 1. • Matriz diagonal: es una matriz cuadrada, en la que todos los elementos no pertenecientes a la diagonal principal son nulos. • Matriz triangular superior: es una matriz donde todos los elementos por debajo de la diagonal son ceros. • Matriz escalar: es una matriz diagonal • Matriz triangular inferior: es una matriz donde todos los elementos de ella son iguales. donde todos los elementos por encima de la diagonal son ceros.

Operaciones con matrices Trasposición de matrices Suma y diferencia de matrices Producto de una matriz por un número Producto de matrices Propiedades simplificativas Matrices inversibles

Operaciones con matrices I 1. - Trasposición de matrices Dada una matriz de orden m x n, A = (aij), se llama matriz traspuesta de A, y se representa por At, a la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A. Es decir: Propiedades de la trasposición de matrices: 1ª. - Dada una matriz A, siempre existe su traspuesta y además es única. 2ª. - La traspuesta de la matriz traspuesta de A es A. a (At)t = A.

Matriz traspuesta: ejemplo y propiedades La traspuesta de una matriz A cualquiera se obtiene cambiando filas por columnas y se representa por At. Si A = (aij), entonces At = (aji). Si A es mxn, entonces At es nxm. æ Ejemplo: Si A = çç è æ 1 1 2 3 t ç entonces A = ç 2 4 5 6 è 3 ö ÷ ÷ ø 4 5 6 ö ÷ ÷ ø Propiedades: I. Para la matriz A, (At)t = A II. Para las matrices A y B, (A + B)t = At + Bt III. Para la matriz A y el número real k, (k. A)t = k. At IV. Para las matrices A y B, (A. B)t = Bt. At V. Si A es una matriz simétrica, At = A

Operaciones con matrices II 2. - Suma y diferencia de matrices La suma de dos matrices A=(aij), B=(bij) de la misma dimensión, es otra matriz S=(sij) de la misma dimensión que los sumandos y con término genérico S = (aij + bij). La suma de las matrices A y B se denota por A+B. Ejemplo Sin embargo, no se pueden sumar. Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión. La diferencia de matrices A y B se representa por A–B, y se define como la suma de A con la opuesta de B : A–B = A + (–B)

Suma de matrices: ej de orden 3 Para sumar dos matrices A y B con las mismas dimensiones se suman los correspondientes elementos: si A = (aij) y B = (bij) entonces A + B = (aij + bij) æ a 11 a 12 a 13 a 14 ö æ b 11 b 12 b 13 b 14 ç ÷ ç A + B = (aij) + (bij) = ç a 21 a 22 a 23 a 24 ÷ + ç b 21 b 22 b 23 b 24 è a 31 a 32 a 33 a 34 ø è b 31 b 32 b 33 b 34 æ a 11 + b 11 ç a = ç 21 + b 21 è a 31 + b 31 a 12 + b 12 a 13 + b 13 a 14 + b 14 a 22 + b 22 a 23 + b 23 a 24 + b 24 a 32 + b 32 a 33 + b 33 a 34 + b 34 ö ÷ ÷ = ø ö ÷ ÷= (aij + bij ) ø

Propiedades de la adición de matrices Sean A, B y C tres matrices del mismo orden. • Asociativa: A + (B + C) = (A + B) + C • Conmutativa: A + B = B + A • Elemento neutro: A + 0 = 0 + A = A donde 0 es la matriz nula. • Elemento opuesto: A + (– A) = (– A) + A = 0 La matriz –A (opuesta) se obtiene cambiando de signo los elementos de A.

Operaciones con matrices III 3. - Producto de un número por una matriz Para multiplicar un número real por una matriz, se multiplican cada uno de los elementos de la matriz por dicho número. Si A = (aij), entonces k. A = (kaij) æ a 11 a 12 a 13 ö æ ka 11 ka 12 ka 13 ö ç ÷ ç a a a. . k A = k (aij) = k·ç 21 22 23 ÷ = ç ka 21 ka 22 ka 23 ÷÷ = (kaij) è a 31 a 32 a 33 ø è ka 31 ka 32 ka 33 ø

Propiedades con la suma y el producto por un número Sean A y B dos matrices del mismo orden y k y h dos números reales. • Distributiva I: k(A + B) = k. A + k. B • Distributiva II: (k + h)A = k. A + h. A • Elemento neutro: 1 · A = A • Asociativa mixta: k(h. A) = (kh)A El conjunto de las matrices m x n con las operaciones suma y producto por un escalar antes definidas, tiene estructura de espacio vectorial

Operaciones con matrices IV 4. - Producto de matrices Dadas dos matrices A y B, su producto es otra matriz P cuyos elementos se obtienen multiplicando las filas de A por las columnas de B (por lo que deben coincidir estas). De manera más formal, los elementos de P son de la forma: Pij = a ik · bkj con k=1, …. n Es evidente que el número de columnas de A debe coincidir con el número de filas de B. Es más, si A tiene dimensión m x n y B dimensión n x p, la matriz P será de orden m x p, Ejemplos: no se pueden multiplicar

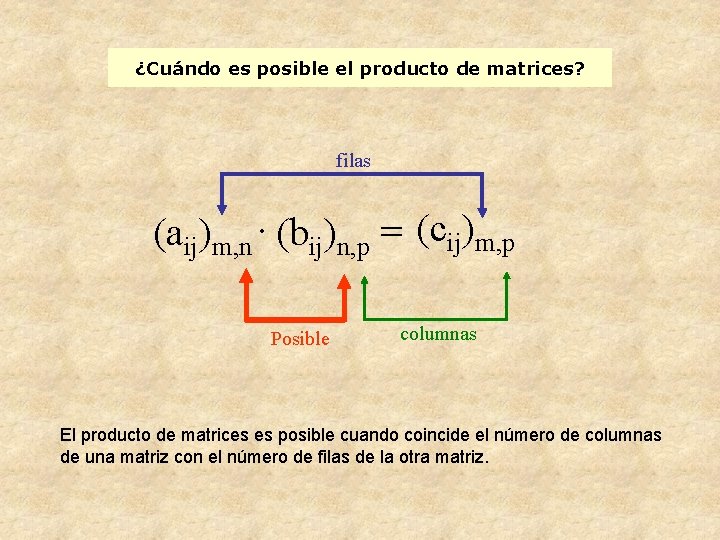
¿Cuándo es posible el producto de matrices? filas (aij)m, n. (bij)n, p = (cij)m, p Posible columnas El producto de matrices es posible cuando coincide el número de columnas de una matriz con el número de filas de la otra matriz.

Producto de matrices: Desarrollo El producto de la matriz A = (a ij) = por la matriz æ a 11 ça ç a 21 ç 31 ç. . è am 1 æ b 11 ç ç b 21 B = (b ij) = ç b 31 ç ç. . çb è n 1 a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö a 23. . . a 2 n ÷ ÷ a 33. . . a 3 n ÷. . . ÷ am 3. . . amn ø b 12 b 13 . . . b 22 b 23 . . . b 32. . b 33. . . . bn 2 bn 3 . . . . b 1 p ö ÷ b 2 p ÷ b 3 p ÷ ÷. . ÷ b np ÷ø es la matriz C = A · B, tal que el elemento que ocupa la posición ij es: cij = ai 1. b 1 j + ai 2. b 2 j +. . . + ain. bnj

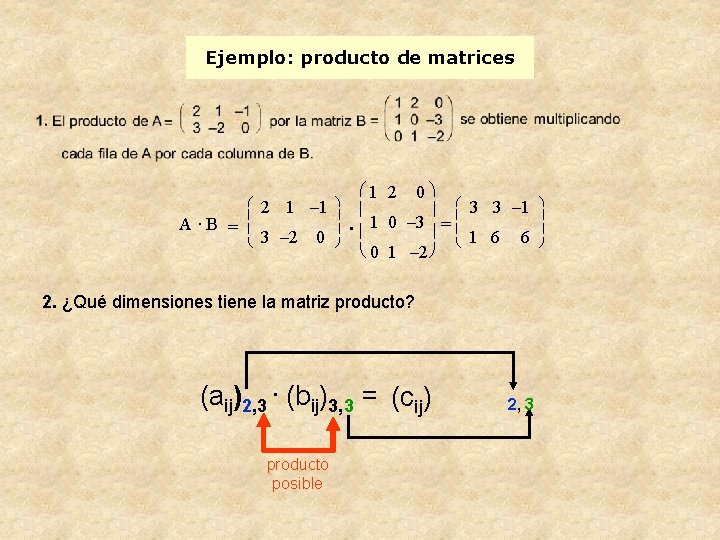
Ejemplo: producto de matrices A ·B = æ ç ç è 2 1 – 1 3 – 2 0 ö ÷ ÷ ø æ 1 2 0ö ç ÷ 1 0 – 3. ç ÷= è 0 1 – 2 ø æ ç ç è 3 3 – 1 1 6 6 2. ¿Qué dimensiones tiene la matriz producto? (aij)2, 3. (bij)3, 3 = (cij) producto posible 2, 3 ö ÷ ÷ ø

Producto: Potencia de una matriz Si A es una matriz cuadrada, las potencias de A, de exponente natural, se definen como en el caso de los números naturales: el exponente indica el número de veces que se multiplica la matriz por sí misma. n veces. A An = A. A. . . Ejemplo: æ 1 1ö ÷÷ = A çç è 0 1ø æ 1 1öæ 1 2 ö æ 1 3 ö ÷÷çç ÷÷ = çç ÷÷ A = A × A = çç è 0 1øè 0 1 ø 3 2 æ 1 1ö æ 1 2 ö ÷÷çç ÷÷ = çç ÷÷ A 2 = A × A = çç è 0 1ø è 0 1 ø æ 1 1ö æ 1 3 ö æ 1 4 ö 3 ÷÷ × çç ÷÷ = × × × = A A A A çç è 0 1ø è 0 1 ø 4 æ 1 1öæ 1 n - 1ö æ 1 n ö n-1 çç ÷÷ = × = An = A A L 3 1 2 1 ø è 0 1øè 0 n- veces

Operaciones con matrices V Inversa de una matriz, Matrices inversibles Una matriz cuadrada que posee inversa se dice que es inversible o regular; en caso contrario recibe el nombre de singular. Dada una matriz cuadrada A de orden n, no siempre existe otra matriz B tal que A·B = B·A = In. Si existe dicha matriz B, se dice que es la matriz inversa de A y se representa por A-1 Propiedades de la matriz inversa I. Si las matrices A y B son inversibles (A. B)– 1 = B– 1. A– 1 II. Si A es una matriz inversible y k 0, (k. A)– 1 = (1/k). A– 1 III. Si A es una matriz inversible, (A– 1)– 1 = A IV. La matriz unidad es inversible y además I– 1 = I V. Si A es una matriz inversible, (A– 1)t = (At)– 1

Métodos de cálculo de la matriz inversa Observación: Podemos encontrar matrices que cumplen A·B = I, pero que B·A ¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha". Hay varios métodos para calcular la matriz inversa de una matriz dada: ØDirectamente ØPor el método de Gauss-Jordan ØUsando determinantes

Inversa de una matriz (directamente) Si A es una matriz cuadrada, se dice que B es la inversa de A si A. B = B. A = I, siendo la matriz unidad. La matriz inversa se representa por A– 1. Ejemplo: æ ö ç 2 – 1 ÷ ç x y ÷ -1 Dada A = çè 1 1 ÷ø para obtener A = çè z t ÷ø se ha de cumplir æ ç ç è 2 – 1 ö÷ æç x y ö÷ æç 1 0 ö÷. 1 1 ÷ø çè z t ÷ø = çè 0 1 ÷ø Y de aquí se deduce que: æ ç ç è ö ÷ ÷ ø 2 x – z 2 y – t 1 0 Û x+z y+t = 0 1 2 x x –z +z 2 y y æ 1 ç 3 -1 Por tanto A = ç– 1 è 3 =1 x = 1/3 =0 y = 1/3 Û –t=0 z = – 1/3 +t=1 t = 2/3 1 3 2 3 ö ÷ ÷ ø

Obtención de la matiz inversa mediante determinantes (I) • La matriz cuadrada A tiene inversa si y sólo si | A | ≠ 0. • Se llama “Adjunto Ai, j” del elemento “ai, j” al determinante del menor Mi, j multiplicado por (-1)i+j • Dada la matriz cuadrada A, se llama “matriz adjunta” de A y se representa adj (A), a la matriz que se obtiene al sustituir cada elemento aij por su adjunto Aij. æ 2 -2 2 ö ç ÷ Ejemplo: Dada la matriz (A) = ç 2 1 0 ÷ , su adjunta sería: è 3 -2 2 ø æ 1 0 – 2 0 2 1 ö ç – 2 2 3 – 2 ÷ ç – 2 2 2 – 2 ÷ æ 2 – 4 – 7 ö ç – – 2 2 3 2 – 3 – 2 ÷ = çç 0 – 2 ÷÷ adj (A)= è – 2 4 6 ø ç ÷ ç – 2 2 2 – 2 ÷ è 1 0 2 1 ø

Obtención de la matiz inversa mediante determinantes (II) Esto es fácil probarlo puesto que sabemos que la suma de los productos de los elementos de una fila por sus adjuntos es el valor del determinante, y que la suma de los productos de los elementos de una fila por los adjuntos de otra fila diferente es 0 æ 2 – 2 2 ö ç ÷ Ejemplo: Dada la matriz A = ç 2 1 0 ÷ , pretendemos encontrar su inversa: è 3 – 2 2 ø La matriz A tiene inversa ya que: det(A) = – 2 0 æ 2 – 4 – 7 ö Ya hemos visto que: adj (A) = ç 0 – 2 ÷ è – 2 4 6 ø æ 2 0 – 2 ö ç ÷ Entonces: [adj (A)] = ç – 4 – 2 4 ÷ è – 7 – 2 6 ø t æ 2 0 – 2 ö æ – 1 0 1 ö 1 1 ç ÷ t Por lo tanto: A = | A | [adj (A)] = – 2 ç – 4 – 2 4 ÷ = ç 2 1 – 2 ÷ è – 7 – 2 6 ø è 7/2 1 – 3 ø – 1

Calculo de la matriz inversa por el método de los adjuntos I

Calculo de la matriz inversa por el método de los adjuntos II