VECTORS VECTORS PROPERTIES OF VECTORS VECTORS Some important

VECTORS

VECTORS PROPERTIES OF VECTORS

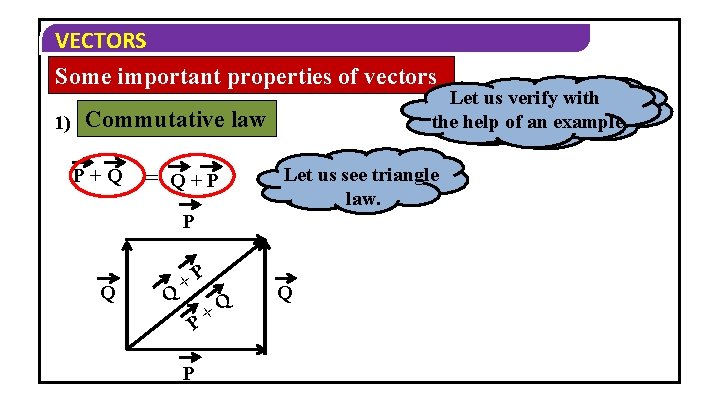
VECTORS Some important properties of vectors 1) Let law us verify with The mathematically the help of an example means… Commutative law P+Q = Q+P Let us see triangle law. P Q Q +P P P +Q Q

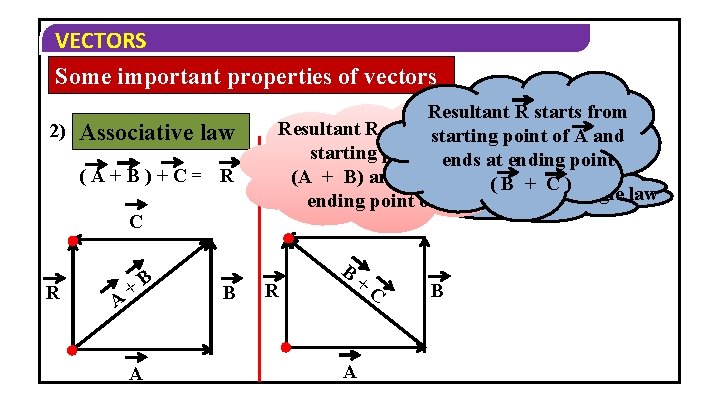
VECTORS Some important properties of vectors 2) Associative law ( A + B ) + C= R C R A +B A Resultant R starts from Let us verify graphically Resultant R startsstarting from point of A and starting point ofends at ending point A(A + ( +B +B)Cand )=R ends at ( B + C ) ending point of. Let C us use the triangle law C B B R + A C B

VECTORS 1) Vector addition obeys……. law. a) commutative b) associative c) distributive d) all the above MCQ S

VECTORS RELATIVE VELOCITY

VECTORS What is relative motion? Relative motion: v The motion of a body with regard to another body is called the relative motion. v The corresponding velocity is called the relative velocity.

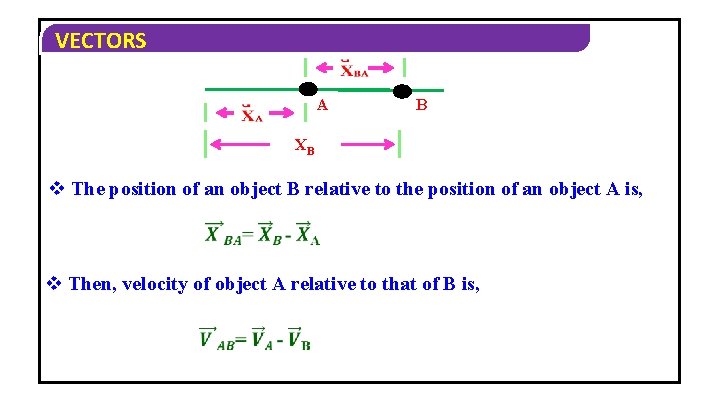
VECTORS A B XB v The position of an object B relative to the position of an object A is, v Then, velocity of object A relative to that of B is,

VECTORS Similarly the velocity of object Magnitude of B relative to that relative velocity, of A is, v when two bodies are moving in the same direction, the relative velocity is equal to the difference of velocities = 00 , cos 00 = 1

VECTORS v when two bodies are moving in the opposite direction, the relative velocity is equal to the sum of their velocities = 1800 , cos 1800 = -1

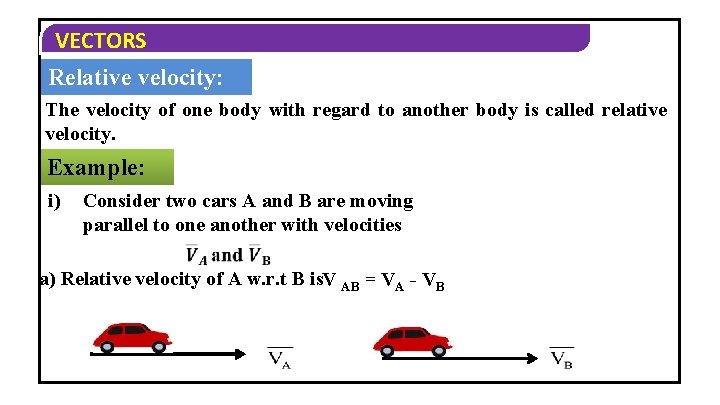
VECTORS Relative velocity: The velocity of one body with regard to another body is called relative velocity. Example: i) Consider two cars A and B are moving parallel to one another with velocities a) Relative velocity of A w. r. t B is. V AB = VA - VB

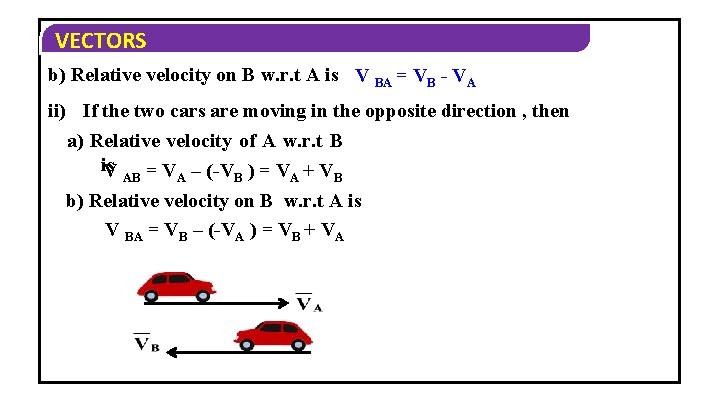
VECTORS b) Relative velocity on B w. r. t A is V BA = VB - VA ii) If the two cars are moving in the opposite direction , then a) Relative velocity of A w. r. t B is V = V – (-V ) = V + V AB A B b) Relative velocity on B w. r. t A is V BA = VB – (-VA ) = VB + VA

VECTORS iii) If the two cars are moving in the mutually perpendicular direction , the relative velocity of A w. r. t B or B w. r. t A is

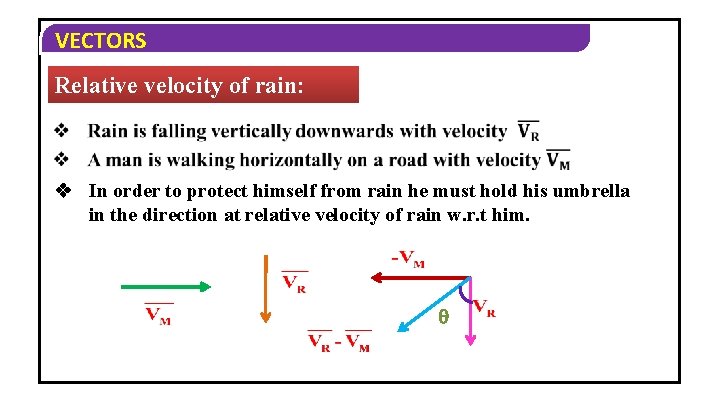
VECTORS Relative velocity of rain: In order to protect himself from rain he must hold his umbrella in the direction at relative velocity of rain w. r. t him.

VECTORS i) Magnitude of relative velocity of rain w. r. t man is ii) Angle made by an umbrella to the vertical is

VECTORS 1) The velocity of one body with regard to another body is called…… a) average velocity b) average speed c) acceleration d) relative velocity MCQ S

VECTORS 2) A car starting from a point travels towards east with a velocity of 36 kmph. Another car starting from the same point travels towards north with a velocity of 24 kmph. The relative velocity of one with respect to another is…. . c) 12 kmph

VECTORS MOTION OF BOAT IN A RIVER

VECTORS Relative velocity of swimmer : a) If the swimming is in the direction of flow of water , then VM = V + V R b) If the swimming is opposite to the flow of water , then VM = V - V R

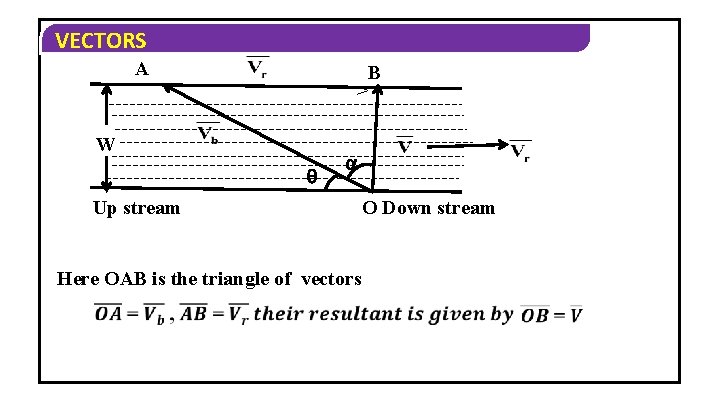
VECTORS Motion of a boat across a river: He is standing on one bank of the river and wants to cross the river then two cases arise.

VECTORS A B > W Up stream Here OAB is the triangle of vectors O Down stream

VECTORS v From the triangle OBA we find v Time taken to cross the river will be given by

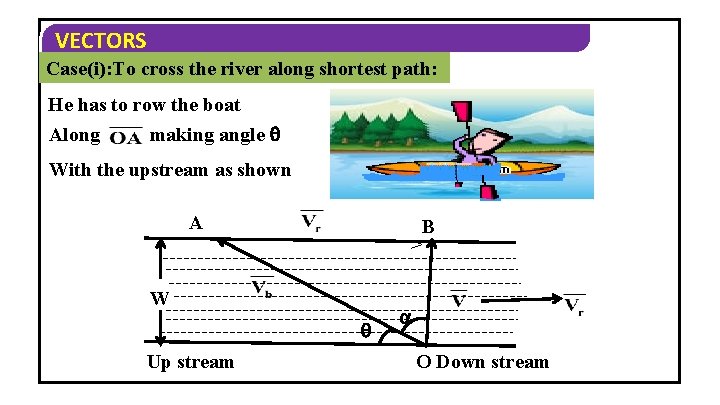
VECTORS Case(i): To cross the river along shortest path: He has to row the boat Along making angle With the upstream as shown A B > W Up stream O Down stream

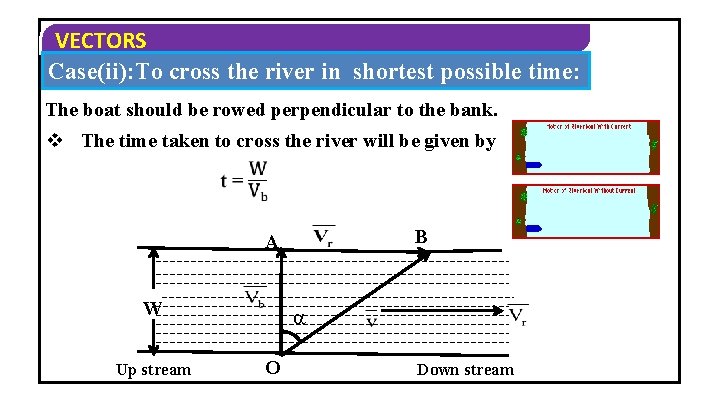
VECTORS Case(ii): To cross the river in shortest possible time: The boat should be rowed perpendicular to the bank. v The time taken to cross the river will be given by B A W Up stream O Down stream

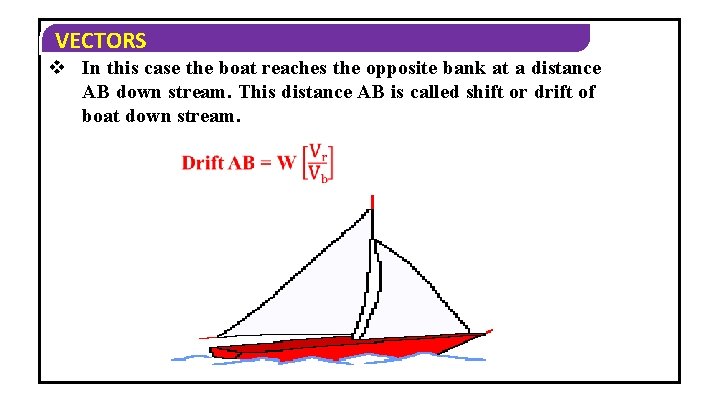
VECTORS v In this case the boat reaches the opposite bank at a distance AB down stream. This distance AB is called shift or drift of boat down stream.

VECTORS 1) A boat takes 2 hours to travel 8 km and back in still water lake with water velocity of 4 kmph. The time taken going upstream of 8 km and coming back is…… MCQ S a) 160 minute b) 80 minute c) 320 minute d) 180 km

VECTORS 2) A motor boat covers the distance between two places on a river and return in 14 hours. If the velocity of boat in still water is 35 kmph. If velocity of the river is 5 kmph then distance between the two places is…. . a) 100 km b) 240 km c) 220 km d) 180 km

VECTORS SCALAR OR DOT PRODUCT

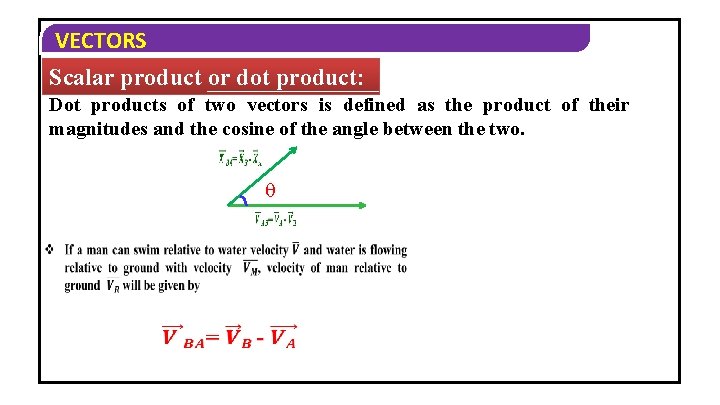
VECTORS Scalar product or dot product: Dot products of two vectors is defined as the product of their magnitudes and the cosine of the angle between the two.

VECTORS

VECTORS Properties of scalar product Ø The dot product between two vectors obeys commutative law Ø Dot product obeys distributive law. i. e, . Ø It is always a scalar which is positive, if angle between the vectors is acute ( i. e, < 900 ) and negative, if angle between them is obtuse (900 < 1800 )

VECTORS Ø Scalar product of two vectors will be maximum When cos = 1 i. e. , = 00 i. e. , vectors are parallel Ø The vectors are orthogonal (perpendicular) = 900

VECTORS

VECTORS Examples: Ø Scalar product of force and displacement is called work done by that force. Ø Dot product between force and velocity vector gives power.

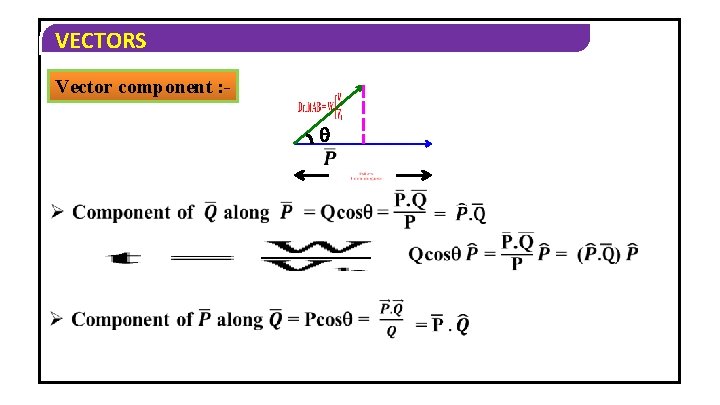
VECTORS Vector component :

VECTORS

VECTORS 1) Dot product of vectors is a. . . a) vector b) scalar c) tensor d) none of these MCQ S

VECTORS 2) If l 1, m 1, n 1 and l 2, m 2, n 2 are the direction cosines of two vectors and is the angle between them, then the value of cos is. . . a) l 1 l 2+m 1 m 2+n 1 n 2 b) l 1 m 1+m 1 n 1+n 1 l 1 c) l 2 m 2+m 2 n 2+n 2 l 2 d) m 1 l 2+l 1 m 2+n 1 m 2

VECTORS a) 72 J b) 24 J solution: S=(4 i-6 j)m = 24 -48 W = -24 J c) -24 J d) zero

VECTORS VECTOR PRODUCT OF TWO VECTORS

VECTORS Multiplication of vector There are two types of vector multiplication Scalar product Dot product Vector product Cross product Now let us learn about the cross product We have already learntorabout the vector product of two dot product of vectors in the vectors. previous lessons

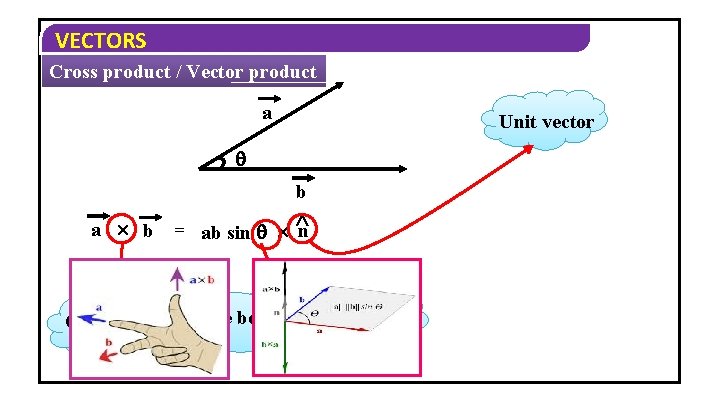
VECTORS Cross product / Vector product a b = ab sin n Cross Product. Angle between two vectors Unit vector

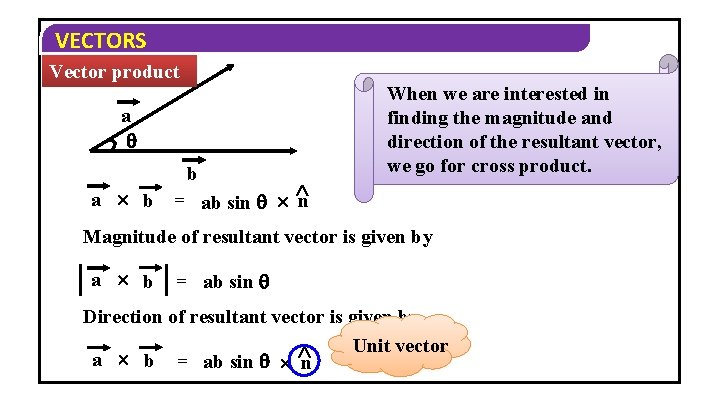
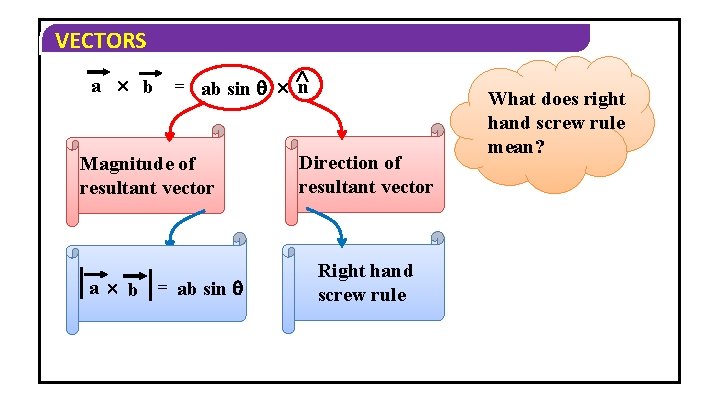
VECTORS Vector product a b = ab sin n When we are interested in finding the magnitude and direction of the resultant vector, we go for cross product. Magnitude of resultant vector is given by a b = ab sin Direction of resultant vector is given by Unit vector a b = ab sin n

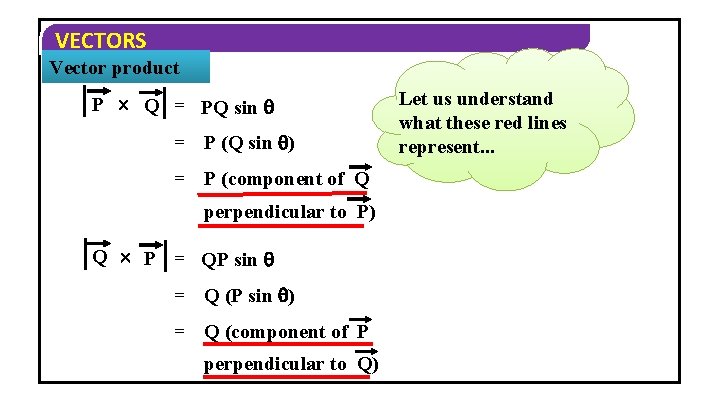
VECTORS Vector product P Q = PQ sin = P (Q sin ) = P (component of Q perpendicular to P) Q P = QP sin = Q (P sin ) = Q (component of P perpendicular to Q) Let us understand what these red lines represent. . .

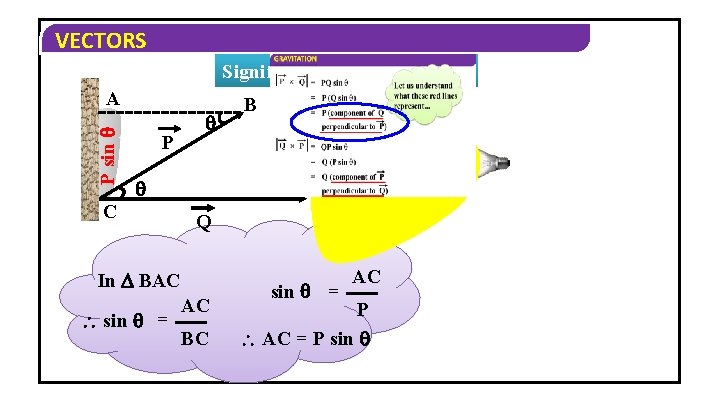
VECTORS Significance of cross product P sin A P B C Q In BAC sin = AC BC sin = AC P AC = P sin

VECTORS a b = ab sin n Magnitude of resultant vector a b = ab sin Direction of resultant vector Right hand screw rule What does right hand screw rule mean?

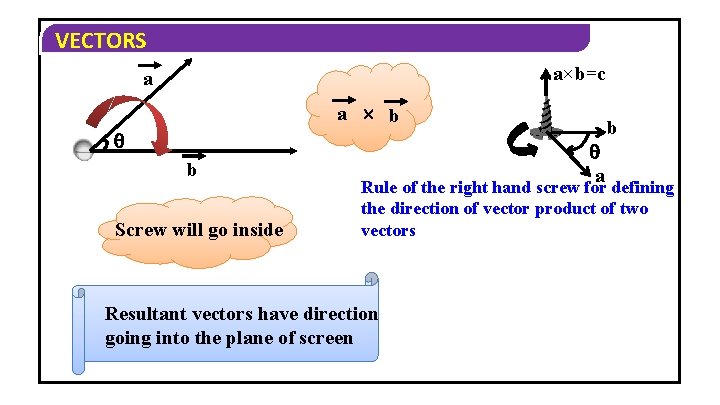
VECTORS a×b=c a a b b Screw will go inside a b Rule of the right hand screw for defining the direction of vector product of two vectors Resultant vectors have direction going into the plane of screen

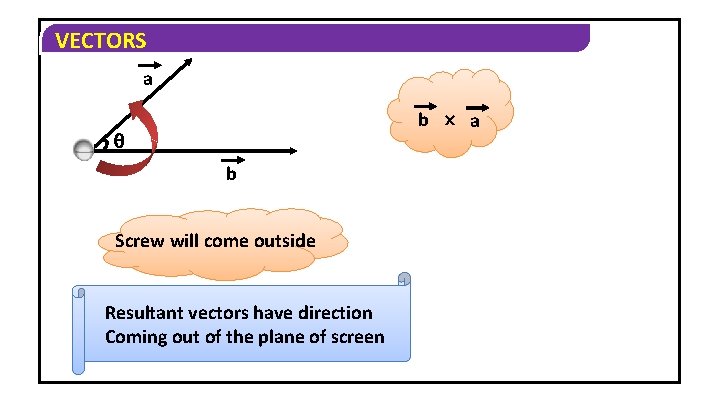
VECTORS a b a b Screw will come outside Resultant vectors have direction Coming out of the plane of screen

VECTORS Characteristics of cross product / vector product 1) The product is a vector 2) If A and B are given, the vector product is, n A B = AB sin ^ 3) It is directed at right angles to the plane containing the two vectors and its sense is given by the right hand thumb rule.

VECTORS Characteristics of vector product / cross product 4) If two vectors are parallel to each other, magnitude of vector product is zero. 5) It does not obey the commutative law of multiplication. 6) The magnitude of self cross product of a vector is zero. i. e. a a = 0

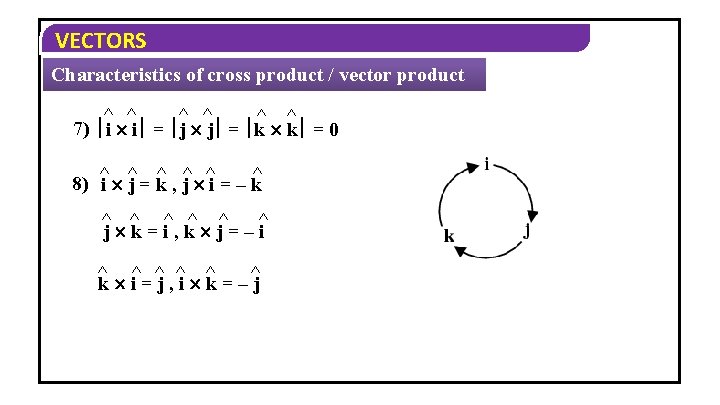
VECTORS Characteristics of cross product / vector product ^ ^ ^ 7) i i = j j = k k = 0 ^ ^ 8) ^i ^ j=k, j i=–k ^ ^ ^ j k=i, k j=–i ^ ^ ^ k i=j, i k=–j

VECTORS 1) If two vectors are parallel to each other then…… a) a b = 0 b) a b = 1 c) a b = 0 d) a b = ∞ MCQ S

VECTORS 2) In vector product ……. . a) ^i = – ^ k b) ^i = 0 ^ ^ ^ c) i i = j d) ^i = k^ MCQ S

VECTORS 3) The cross product of j×i = ……. . a) 0 b) 1 c) -k d) k MCQ S

VECTORS EXPRESSION OF VECTOR IN DETERMINANT FORM

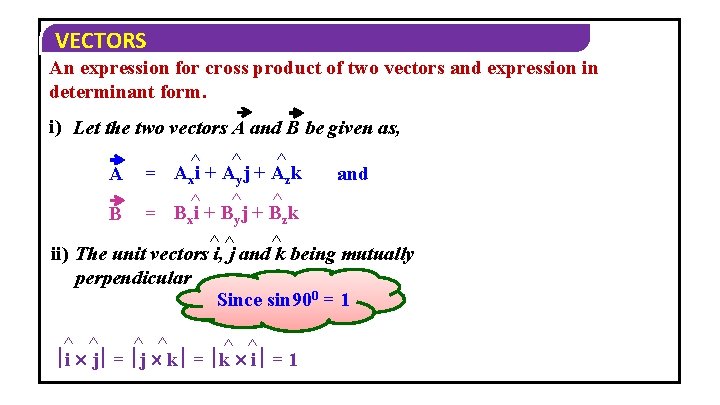
VECTORS An expression for cross product of two vectors and expression in determinant form. i) Let the two vectors A and B be given as, ^ ^ ^ = Ax i + A y j + A z k and ^ ^ ^ B B = xi + B yj + B zk ^^ ^ ii) The unit vectors i, j and k being mutually perpendicular Since sin 900 = 1 A ^ ^ ^ i j = j k = k i = 1

VECTORS ^ ^ ^ i j = k, a unit vector perpendicular to both i and j ^ ^ ^ j k = i, a unit vector perpendicular to both j and k ^ ^ ^ k i = j, a unit vector perpendicular to both k and i Since vector product is not commutative, ^ ^ ^ k j = –i and i k = –j ^ ^ ^ = j k i Since vector product of a vector with itself is zero, ^ ^ ^ j k = i, ^ ^ ^ i i = j j = k k = 0

VECTORS ^ ^ ^ A B =Ax Bx i i + Ax By i j + Ax Bz i k + ^ ^^ ^^ Ay B x ^ j i + Ay By j j + Ay Bz j k + ^ ^ ^ Az Bx ^k ^i + Az By ^ k j + Az Bz k k = Ax B x 0 + Ax B y ^ k + Ax B z ^ +A B 0 + A B Ay Bx –k y y y z ^ Az Bx j + Az By –i^ + Az Bz ^ + –j ^ + i 0 ^ ^ ^ j ( A B – A B ) A B =( Ay. Bz– Az. By) i + z x x z + x y y x k

VECTORS Alternate method: ^ ^ ^ A B = ( Ay B z – Az B y ) i + ( Az B x – Ax B z ) j + ( Ax B y – Ay B x ) k Using the determinant method A B = ^ i Ax Bx ^ j Ay By ^ k Az Bz

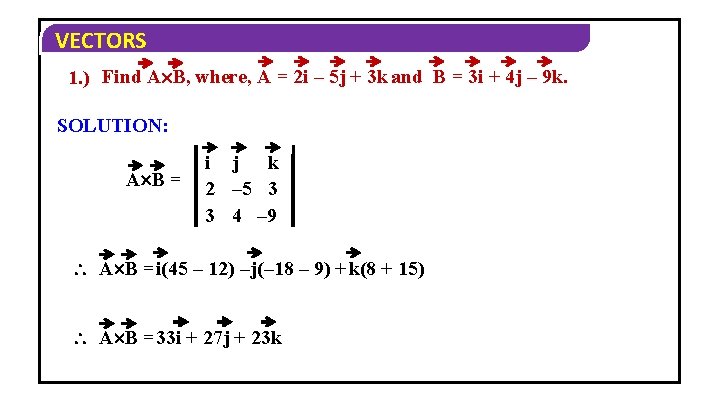
VECTORS 1. ) Find A B, where, A = 2 i – 5 j + 3 k and B = 3 i + 4 j – 9 k. a) 33 i + 27 j + 23 k b) 30 i + 25 j + 23 k c) 33 i + 28 j + 23 k d) 33 i + 27 j + 25 k MCQ S

VECTORS 1. ) Find A B, where, A = 2 i – 5 j + 3 k and B = 3 i + 4 j – 9 k. SOLUTION: A B = i j k 2 – 5 3 3 4 – 9 A B =i(45 – 12) –j(– 18 – 9) + k(8 + 15) A B =33 i + 27 j + 23 k

VECTORS 2) A force F = (4 i + 2 j – k)N acts on a body at a distance of Q = (–i – 3 j + k) From the origin of an inertial reference frame, find the torque acting on the body. a) (i + 3 j + 10 k) N-m b) (i + j + 10 k) N-m c) (i + j + 15 k) N-m d) (3 i + j + 15 k) N-m

VECTORS 2) A force F = (4 i + 2 j – k)N acts on a body at a distance of Q = (–i – 3 j + k) From the origin of an inertial reference frame, find the torque acting on the body. The torque acting on the body is given by, =r F i = – 1 4 j – 3 2 k 1 – 1 = i(3 – 2) – j(1 – 4) + k(– 2 + 12) = (i + 3 j + 10 k) N-m

VECTORS Thank you…