Matrices and Determinants Copyright Cengage Learning All rights

Matrices and Determinants Copyright © Cengage Learning. All rights reserved. 10

10. 5 APPLICATIONS OF MATRICES AND DETERMINANTS Copyright © Cengage Learning. All rights reserved.

What You Should Learn • Use Cramer’s Rule to solve systems of linear equations. • Use determinants to find the areas of triangles. • Use a determinant to test for collinear points and find an equation of a line passing through two points. • Use matrices to encode and decode messages. 3

Cramer’s Rule 4 4

Cramer’s Rule In this section, you will study one more method, Cramer’s Rule, named after Gabriel Cramer. This rule uses determinants to write the solution of a system of linear equations. 5

Cramer’s Rule There, it was pointed out that the system a 1 x + b 1 y = c 1 a 2 x + b 2 y = c 2 has a solution and provided that a 1 b 2 – a 2 b 1 0. 6

Cramer’s Rule Each numerator and denominator in this solution can be expressed as a determinant, as follows. Relative to the original system, the denominator for x and y is simply the determinant of the coefficient matrix of the system. This determinant is denoted by D. 7

Cramer’s Rule The numerators for x and y are denoted by Dx and Dy, respectively. They are formed by using the column of constants as replacements for the coefficients of x and y, as follows. Coefficient Matrix D Dx Dy 8

Cramer’s Rule For example, given the system 2 x – 5 y = 3 – 4 x + 3 y = 8 the coefficient matrix, D, Dx, and Dy are as follows. Coefficient Matrix D Dx Dy 9

Cramer’s Rule generalizes easily to systems of n equations in n variables. The value of each variable is given as the quotient of two determinants. The denominator is the determinant of the coefficient matrix, and the numerator is the determinant of the matrix formed by replacing the column corresponding to the variable (being solved for) with the column representing the constants. 10

Cramer’s Rule For instance, the solution for x 3 in the following system is shown. 11

Cramer’s Rule 12

Example 1 – Using Cramer’s Rule for a 2 2 System Use Cramer’s Rule to solve the system of linear equations. 4 x – 2 y = 10 3 x – 5 y = 11 Solution: To begin, find the determinant of the coefficient matrix. D= = – 20 – (– 6) = – 14 13

Example 1 – Solution cont’d Because this determinant is not zero, you can apply Cramer’s Rule. So, the solution is x = 2 and y = – 1. Check this in the original system. 14

Cramer’s Rule Remember that Cramer’s Rule does not apply when the determinant of the coefficient matrix is zero. This would create division by zero, which is undefined. 15

Area of a Triangle 16 16

Area of a Triangle Another application of matrices and determinants is finding the area of a triangle whose vertices are given as points in a coordinate plane. 17

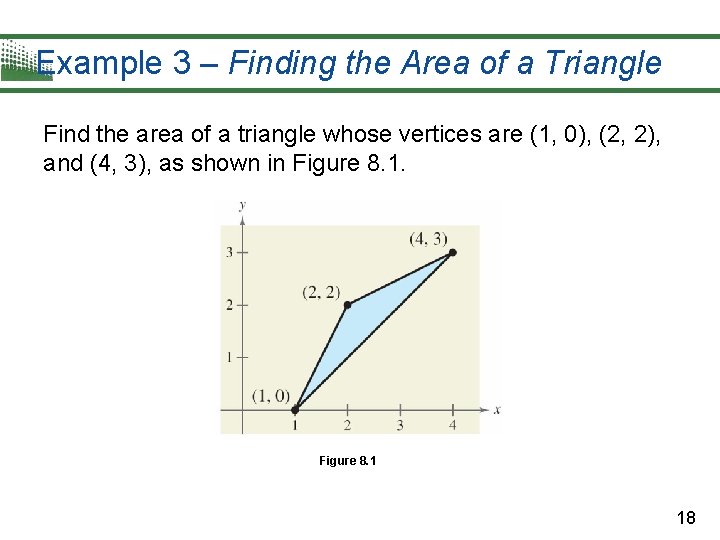
Example 3 – Finding the Area of a Triangle Find the area of a triangle whose vertices are (1, 0), (2, 2), and (4, 3), as shown in Figure 8. 1 18

Example 3 – Solution Let (x 1, y 1) = (1, 0), (x 2, y 2) = (2, 2), and (x 3, y 3) = (4, 3). Then, to find the area of the triangle, evaluate the determinant. 19

Example 3 – Solution cont’d Using this value, you can conclude that the area of the triangle is Choose (–) so that the area is positive. 20

Lines in a Plane 21 21

Lines in a Plane What if the three points in Example 3 had been on the same line? What would have happened had the area formula been applied to three such points? The answer is that the determinant would have been zero. Consider, for instance, the three collinear points (0, 1), (2, 2), and (4, 3), as shown in Figure 8. 2 22

Lines in a Plane The area of the “triangle” that has these three points as vertices is 23

Lines in a Plane The result is generalized as follows. 24

Example 4 – Testing for Collinear Points Determine whether the points (– 2, – 2), (1, 1), and (7, 5) are collinear. (See Figure 8. 3. ) Figure 8. 3 25

Example 4 – Solution Letting (x 1, y 1) = (– 2, – 2), (x 2, y 2) = (1, 1), and (x 3, y 3) = (7, 5), you have 26

Example 4 – Solution cont’d Because the value of this determinant is not zero, you can conclude that the three points do not lie on the same line. Moreover, the area of the triangle with vertices at these points is square units. 27

Lines in a Plane The test for collinear points can be adapted to another use. That is, if you are given two points on a rectangular coordinate system, you can find an equation of the line passing through the two points, as follows. 28

Cryptography 29 29

Cryptography A cryptogram is a message written according to a secret code. (The Greek word kryptos means “hidden. ”) Matrix multiplication can be used to encode and decode messages. To begin, you need to assign a number to each letter in the alphabet (with 0 assigned to a blank space), as follows. 0=_ 1=A 2=B 3=C 4=D 5=E 6=F 7=G 8=H 9=I 10 = J 11 = K 12 = L 13 = M 14 = N 30

Cryptography 15 = O 16 = P 17 = Q 18 = R 19 = S 20 = T 21 = U 22 = V 23 = W 24 = X 25 = Y 26 = Z Then the message is converted to numbers and partitioned into uncoded row matrices, each having n entries, as demonstrated in Example 6. 31

Example 6 – Forming Uncoded Row Matrices Write the uncoded row matrices of order 1 3 for the message MEET ME MONDAY. Solution: Partitioning the message (including blank spaces, but ignoring punctuation) into groups of three produces the following uncoded row matrices. [13 5 5] [20 0 13] [5 0 13] [15 14 4] [1 25 0] M E E T M E M O N D A Y Note that a blank space is used to fill out the last uncoded row matrix. 32

Cryptography To encode a message, use the techniques to choose an n n invertible matrix such as and multiply the uncoded row matrices by A (on the right) to obtain coded row matrices. Here is an example. Uncoded Matrix [13 5 5] Encoding Matrix A Coded Matrix = [13 – 26 21] 33