MATRICES Y DETERMINANTES MATRICES Una matriz es todo

MATRICES Una matriz es todo arreglo rectangular de números reales definidos en filas y/o

NOTACION MATRICIAL Las matrices se denotan por letras mayúsculas y los elemento se designan

NOTACION MATRICIAL Así notamos: Ø En la matriz A: a 11=5 Columna 1 Fila

NOTACION MATRICIAL Así notamos: En la matriz B: b 21 =2 Columna 1 Fila

FILAS Y COLUMNAS DE UNA MATRIZ El arreglo de los elementos en cualquier línea

DIMENSION U ORDEN DE UNA MATRIZ Esta definida por el número de filas o

En las siguientes alternativas entre paréntesis ponga V si es verdadero y F si

TIPOS DE MATRICES ESPECIALES MATRIZ VECTOR Es un arreglo que tiene únicamente un renglón

TIPOS DE MATRICES ESPECIALES MATRIZ RECTANGULAR Es una matriz cuyo número de renglones es

TIPOS DE MATRICES ESPECIALES MATRIZ NULA O CERO Es una matriz con todos los

TIPOS DE MATRICES ESPECIALES MATRIZ CUADRADA Es una matriz que tiene el mismo número

TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR Estas matrices se dividen en: üMatriz Triangular superior

TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR SUPERIOR Es una matriz cuadrada que tiene todos

TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR INFERIOR Es una matriz cuadrada que tiene todos

TIPOS DE MATRICES ESPECIALES MATRIZ SIMETRICA Toda matriz cuadrada es simétrica, si los elementos

TIPOS DE MATRICES ESPECIALES MATRIZ DIAGONAL Es una matriz cuadrada que tiene todos sus

TIPOS DE MATRICES ESPECIALES MATRIZ ESCALAR Es una matriz cuadrada que tiene todos sus

TIPOS DE MATRICES ESPECIALES MATRIZ IDENTIDAD Es una matriz cuadrada que tiene todos sus

TIPOS DE MATRICES ESPECIALES MATRIZ TRANSPUESTA Sea A una matriz de orden m x

TIPOS DE MATRICES ESPECIALES MATRIZ ANTISEMETRICA Es una matriz cuadrada cuyos elementos opuestos a

IGUALDAD DE MATRICES MATRIZ ANTISEMETRICA Dos matrices son iguales si: 1. Tienen igual dimensión.

Slides: 26

Download presentation

MATRICES Y DETERMINANTES

MATRICES Una matriz es todo arreglo rectangular de números reales definidos en filas y/o columnas entre paréntesis o corchetes. Así tenemos:

NOTACION MATRICIAL Las matrices se denotan por letras mayúsculas y los elemento se designan con aij. Donde: i = es la i – ésima fila o renglón j= es la j – ésima columna

NOTACION MATRICIAL Así notamos: Ø En la matriz A: a 11=5 Columna 1 Fila 1

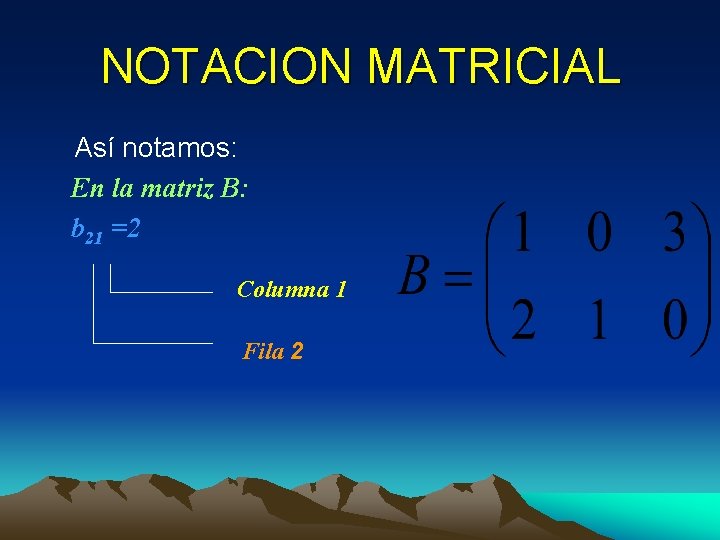
NOTACION MATRICIAL Así notamos: En la matriz B: b 21 =2 Columna 1 Fila 2

FILAS Y COLUMNAS DE UNA MATRIZ El arreglo de los elementos en cualquier línea horizontal forman un renglón o fila de la matriz. Ej: Renglón o fila 1 Renglón o fila 2 Renglón o fila 3

FILAS Y COLUMNAS DE UNA MATRIZ El arreglo de los elementos en cualquier línea vertical forman un columna de la matriz. Ej: Columna 2 Columna 1

DIMENSION U ORDEN DE UNA MATRIZ Esta definida por el número de filas o renglón y el número de columnas. Ej: De: tenemos: A tiene 3 filas y 2 columnas

DIMENSION U ORDEN DE UNA MATRIZ Esta definida por el número de filas o renglón y el número de columnas. Ej: De: tenemos: B tiene 2 filas y 3 columnas

DIMENSION U ORDEN DE UNA MATRIZ Esta definida por el número de filas o renglón y el número de columnas. Ej: De: tenemos: A tiene 3 fila y 3 columnas

En las siguientes alternativas entre paréntesis ponga V si es verdadero y F si es falso a) a 22 = b 22 (V) b) a 12 < b 21 (V) c) a 23 + b 12= a 13 (V) d) a 12+ a 23 > b 12 (F) e) A (aij)3 x 2 (F) f) B (bij))2 x 2 (V) g) Los elementos del primer renglón de la matriz A son 2 y 1 (F)

TIPOS DE MATRICES ESPECIALES MATRIZ VECTOR Es un arreglo que tiene únicamente un renglón o una columna. Ej: Matriz renglón M a t r i z c o l u m n a

TIPOS DE MATRICES ESPECIALES MATRIZ RECTANGULAR Es una matriz cuyo número de renglones es diferentes de las columnas, es decir m n

TIPOS DE MATRICES ESPECIALES MATRIZ NULA O CERO Es una matriz con todos los elementos ceros. Ej:

TIPOS DE MATRICES ESPECIALES MATRIZ CUADRADA Es una matriz que tiene el mismo número de renglones y columnas es decir m=n. Ej:

TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR Estas matrices se dividen en: üMatriz Triangular superior üMatriz Triangular Inferior.

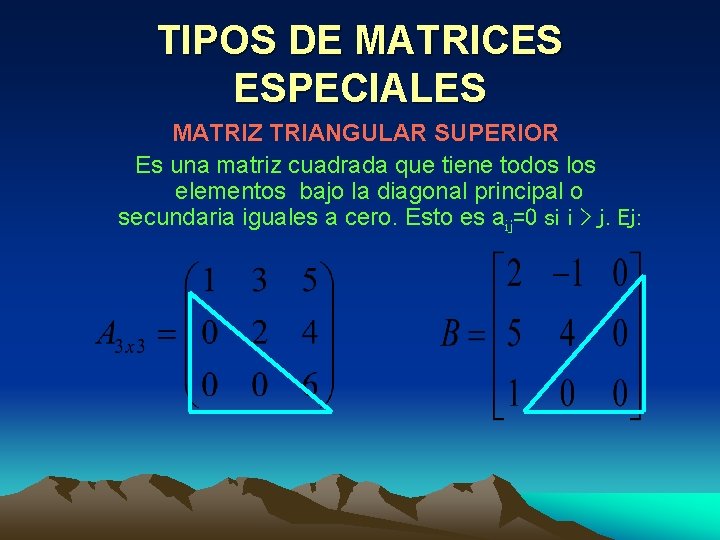
TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR SUPERIOR Es una matriz cuadrada que tiene todos los elementos bajo la diagonal principal o secundaria iguales a cero. Esto es aij=0 si i > j. Ej:

TIPOS DE MATRICES ESPECIALES MATRIZ TRIANGULAR INFERIOR Es una matriz cuadrada que tiene todos los elementos sobre la diagonal principal iguales a cero. Esto es aij=0 si i < j. Ej:

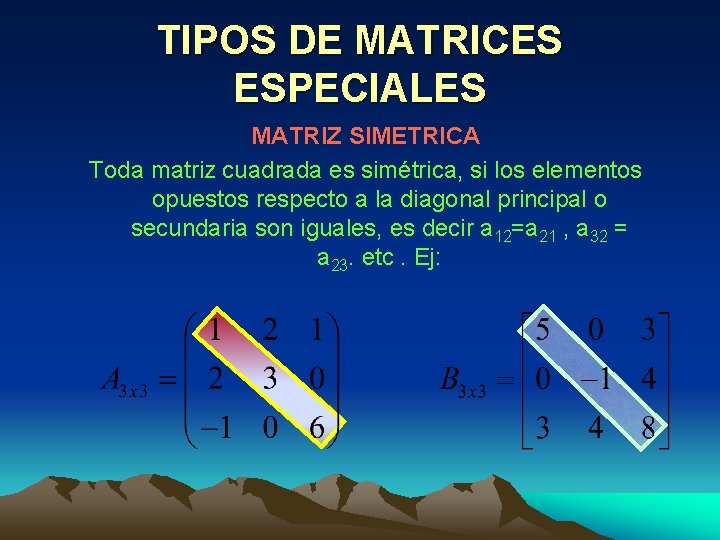
TIPOS DE MATRICES ESPECIALES MATRIZ SIMETRICA Toda matriz cuadrada es simétrica, si los elementos opuestos respecto a la diagonal principal o secundaria son iguales, es decir a 12=a 21 , a 32 = a 23. etc. Ej:

TIPOS DE MATRICES ESPECIALES MATRIZ DIAGONAL Es una matriz cuadrada que tiene todos sus elementos sobre y debajo de la diagonal principal igual a cero. Esto es aij=0 si i = j. Toda matriz diagonal es una matriz triangular superior e inferior a la vez. Ej: Nota: Algún elemento de la diagonal principal puede ser cero, pero no todos

TIPOS DE MATRICES ESPECIALES MATRIZ ESCALAR Es una matriz cuadrada que tiene todos sus elementos sobre y debajo de la diagonal principal igual a cero, y los elementos de la diagonal principal son iguales entre sí. Esto es aij=0 si i = j, aij=k con k Ej:

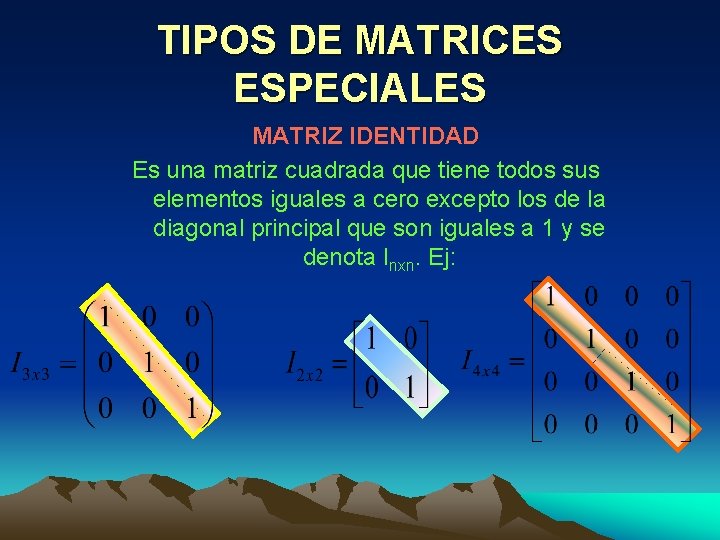
TIPOS DE MATRICES ESPECIALES MATRIZ IDENTIDAD Es una matriz cuadrada que tiene todos sus elementos iguales a cero excepto los de la diagonal principal que son iguales a 1 y se denota Inxn. Ej:

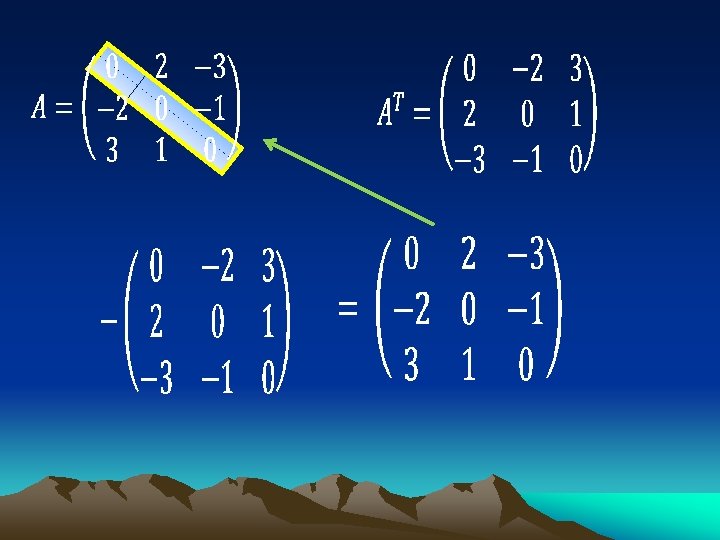
TIPOS DE MATRICES ESPECIALES MATRIZ TRANSPUESTA Sea A una matriz de orden m x n, la transpuesta “A” es de orden n x m, es decir las filas se transforman en columnas. La matriz transpuesta se denota Ej: Sea hallar F 1 = C 1 F 2 = C 2 F 3 = C 3

TIPOS DE MATRICES ESPECIALES MATRIZ ANTISEMETRICA Es una matriz cuadrada cuyos elementos opuestos a la diagonal principal, son valores opuestos. Los elementos de la diagonal son todos cero En la matriz antisimétrica se cumple que: 1. 2.

IGUALDAD DE MATRICES MATRIZ ANTISEMETRICA Dos matrices son iguales si: 1. Tienen igual dimensión. 2. Los elementos correspondientes son iguales. TALLER DE MATRICES 3. docx