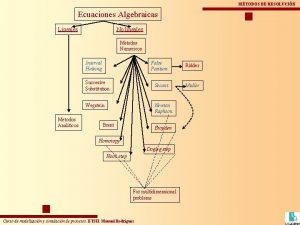
Matrices Determinantes Sistemas de Ecuaciones lineales Definicin Una
























- Slides: 26

Matrices – Determinantes Sistemas de Ecuaciones lineales

Definición: Una matriz es un arreglo rectangular de números. Los números que forman la matriz se llaman entradas o elementos y se escriben dentro de paréntesis. Las matrices se identifican con letras mayúsculas. Ejemplos de matrices: Las líneas horizontales de números se conoce como filas y las verticales como columnas. fila columna

Al número de filas por el número de columnas de una matriz se le llama el orden o tamaño de la matriz. Matriz 2 x 2 Matriz 3 x 3 Matriz 2 x 3 Una matriz puede tener cualquier número finito de filas y de columnas.

Definición de matriz mxn: Un arreglo rectangular de números que tiene m filas y n columnas se conoce como una matriz m x n. Los elementos de la matriz se expresan de la forma aij donde i corresponde a la posición de la fila y j corresponde a la posición de la columna. Una matriz mxn se suele escribir en la forma general abreviada,

Definición de un vector fila: Una matriz que tiene una sola fila se llama vector fila. Ejemplo: vector fila 1 x 4 Definición de un vector columna: Una matriz que tiene una sola columna se llama vector columna. Ejemplo: vector columna 3 x 1 Aclaración: No confunda la notación aij de un elemento con la notación de una matriz.

Definición : Dos matrices son iguales si tienen el mismo tamaño y los mismos elementos. Ejemplo: Definición : La traspuesta de una matriz mxn, A es la matriz nxm cuya fila i es la columna j de A. La traspuesta de A se denota por AT. Ejemplo:

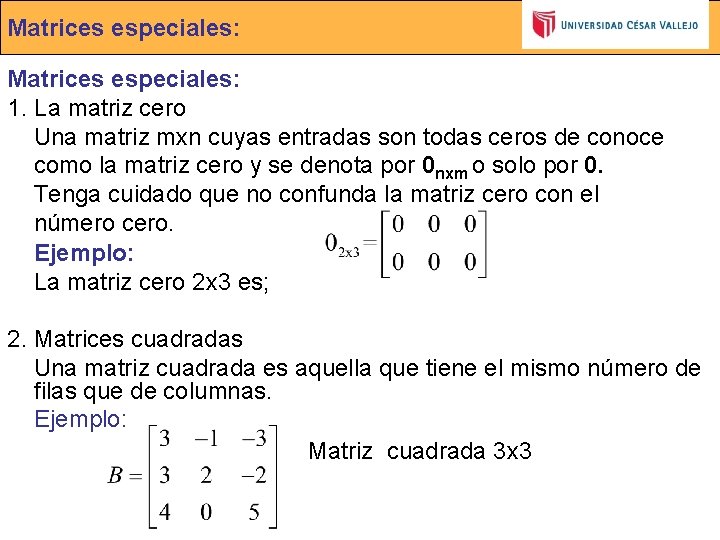
Matrices especiales: 1. La matriz cero Una matriz mxn cuyas entradas son todas ceros de conoce como la matriz cero y se denota por 0 nxm o solo por 0. Tenga cuidado que no confunda la matriz cero con el número cero. Ejemplo: La matriz cero 2 x 3 es; 2. Matrices cuadradas Una matriz cuadrada es aquella que tiene el mismo número de filas que de columnas. Ejemplo: Matriz cuadrada 3 x 3

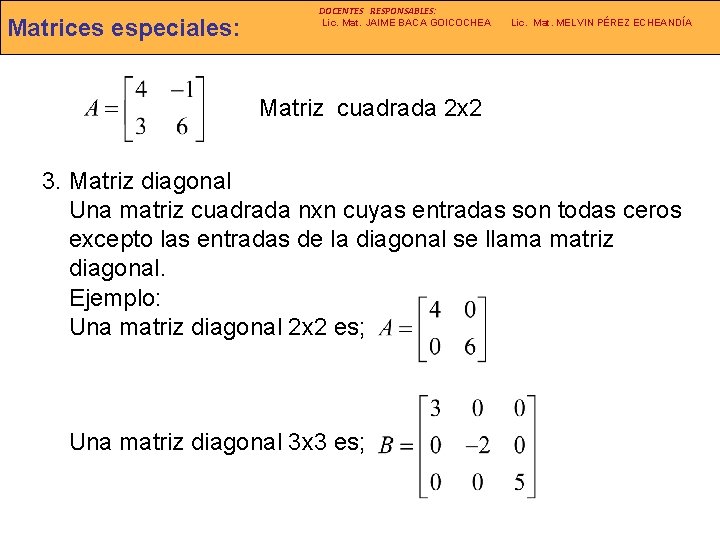
Matrices especiales: DOCENTES RESPONSABLES: Lic. Mat. JAIME BACA GOICOCHEA Lic. Mat. MELVIN PÉREZ ECHEANDÍA Matriz cuadrada 2 x 2 3. Matriz diagonal Una matriz cuadrada nxn cuyas entradas son todas ceros excepto las entradas de la diagonal se llama matriz diagonal. Ejemplo: Una matriz diagonal 2 x 2 es; Una matriz diagonal 3 x 3 es;

Matrices especiales: 4. Matrices triangularizadas Una matriz se dice que está triangularizada por arriba si todas las entradas bajo la diagonal principal son cero. Una matriz se dice que está triangularizada por abajo si todas las entradas sobre la diagonal principal son cero. Ejemplos: Una matriz triangularizada por arriba es; Una matriz triangularizada por abajo es;

Matrices especiales: DOCENTES RESPONSABLES: Lic. Mat. JAIME BACA GOICOCHEA Lic. Mat. MELVIN PÉREZ ECHEANDÍA 5. Matriz identidad Una matriz cuadrada cuyas entradas son todas cero excepto las de la diagonal principal que tiene entradas iguales a 1, se llama matriz identidad. Existe una matriz identidad para cada tamaño de matriz cuadrada nxn. Ejemplos: La matriz identidad 2 x 2 es; La matriz identidad 3 x 3 es; La matriz identidad 4 x 4 es;

Operaciones con matrices: 1. Suma de matrices La suma de matrices se obtiene sumando las entradas correspondientes de las dos matrices. Observe que la suma está bién definida si las dos matrices tienen el mismo tamaño. Ejemplos: Encuentra la suma las matrices.

Operaciones con Matrices :

Propiedadesde de matrices nxm: Propiedades nxm: 1. A + B = B + A, propiedad conmutativa. 2. A + (B + C) = (A + B) + C, propiedad asociativa 3. A + 0 = 0 + A , propiedad de identidad 4. (A + B)T = AT + BT propiedad de las transpuestas Ejemplos: a. Demuestra que A + B = B + A.

Propiedades de matrices nxm: b. Demuestra que A + (B + C) = (A +B) + C.

Propiedades de matrices nxm: c. Demuestra que A + 0 = A. Definición de la multiplicación escalar: Si es una matriz mxn y k es un número real (un escalar) definimos y denotamos la multiplicación escalar de A y k por, . La multiplicación escalar se obtiene multiplicando cada entrada o elemento de la matriz A por el escalar k.

Lamultiplicaciónde dematrices: La Para definir la multiplicación de dos matrices necesitamos definir la multiplicación de un vector fila por un vector columna y determinar los tamaños de las matrices que se pueden multiplicar. Definición del producto interno de vectores El producto interno de un vector fila de tamaño, 1 xp, por un vector columna de tamaño, px 1, se denota y define por, Observa que el producto interno de un vector fila por un vector columna produce un número real.

La multiplicación de matrices : Ejemplo: Encuentra el producto interno de los siguientes vectores. Ojo: El resultado del producto interno es un número real y el número de columnas del primer vector debe ser igual al número de filas del segundo.

La multiplicación de matrices : Definición de la multiplicación de matrices Sea A una matriz de tamaño nxp, y sea B una matriz de tamaño pxm. Definimos y denotamos la multiplicación de A y B por A. B = C, donde C es la matriz de tamaño nxm cuyas entradas cij son el producto interno de la fila i por la columna j. Ejemplo: Encuentra los productos AB y BA de las siguientes matrices.

La multiplicación de matrices :

La multiplicación de matrices :

La multiplicación de matrices : Propiedades de la multiplicación de matrices Si AB y C son matrices para las cuales la multiplicación esta definida y k es un número real (escalar): 1. A(BC) = (AB)C propiedad asociativa 2. A( B + C ) = AB + AC propiedad distributiva 3. ( A + B )C = AC + BC propiedad distributiva 4. (k. A)B = k(AB) asociativa escalar Ejemplo: Demuestra las siguientes igualdades.

La multiplicación de matrices:

La multiplicación de matrices : Ejemplos: 9. ¿Qué tamaño tienen las matrices AB y BA si A es una matriz 3 x 4 y B es una matriz 4 x 3? 10. ¿Qué tamaño tienen las matrices AB y BA si A es una matriz 5 x 4 y B es una matriz 3 x 5?

La inversa de una matriz: La matriz identidad La matriz cuadrada diagonal nxn cuyas entradas en la diagonal principal son todas 1 y las demás entradas son todas 0 se conoce como la matriz identidad nxn. La inversa de una matriz Sea A una matriz cuadrada nxn. Si existe una matriz B, nxn tal que AB = BA = In, decimos que B es la matriz inversa de A y la denotamos por B = A-1.

La inversa de una matriz: Ejemplos: 1. Verifica que la matriz inversa de 2. Verifica que la matriz inversa de es Procedimiento para encontrar la inversa de una matriz Si A es una matriz invertible nxn construya la matriz aumentada. La matriz inversa A-1, nxn, se obtiene reduciendo la matriz mediante operaciones elementales de filas hasta obtener la matriz. Ejemplos: 1. Encuentra la matriz inversa de . .

La inversa de una matriz: Para ello planteamos el sistema de ecuaciones: La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil comprobar que también cumple A-1 · A = I, con lo cual es realmente la inversa de A. Calcular la inversa de las siguientes matrices
 Objetivo general de las ecuaciones lineales
Objetivo general de las ecuaciones lineales Sistemas de ecuaciones lineales
Sistemas de ecuaciones lineales Que son ecuaciones algebraicas
Que son ecuaciones algebraicas Unidad 4 sistemas de ecuaciones diferenciales lineales
Unidad 4 sistemas de ecuaciones diferenciales lineales Ejemplos de ecuaciones lineales en una empresa
Ejemplos de ecuaciones lineales en una empresa Lenguaje algebraico ejemplos
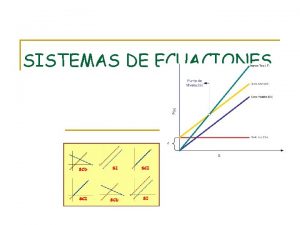
Lenguaje algebraico ejemplos Resolver gráficamente el siguiente sistema de ecuaciones:
Resolver gráficamente el siguiente sistema de ecuaciones: Ecuación condicional
Ecuación condicional Como construir una ecuacion
Como construir una ecuacion Ecuaciones lineales
Ecuaciones lineales Solucion no trivial
Solucion no trivial Ecuaciones exponenciales logarítmicas
Ecuaciones exponenciales logarítmicas Como se resuelve una ecuacion
Como se resuelve una ecuacion Edo
Edo Sistema de ecuaciones lineales definición
Sistema de ecuaciones lineales definición Sistema de ecuaciones lineales definición
Sistema de ecuaciones lineales definición Método de suma y resta ejemplos
Método de suma y resta ejemplos Ecuaciones lineales
Ecuaciones lineales Sistemas lineales invariantes en el tiempo
Sistemas lineales invariantes en el tiempo Determinante de una matriz
Determinante de una matriz Diferencia entre matriz y determinante
Diferencia entre matriz y determinante Imagenes
Imagenes Definicin de estado
Definicin de estado Unnime
Unnime Los monemas son
Los monemas son Sexo definicin
Sexo definicin Definicin de amor
Definicin de amor