The Complexity of Minimizing Certain Cost Metrics for

The Complexity of Minimizing Certain Cost Metrics for k-Source Spanning Trees Harold S. Connamacher Andrzej Proskurowski 劉效飛 田文錦 蕭志亘 林容任 王弘倫 胡淑瓊

Harold S. Connamacher Graduate Student Department of Computer Science University of Toronto Andrzej Proskurowski Professor Computer Science Dept. University of Oregon

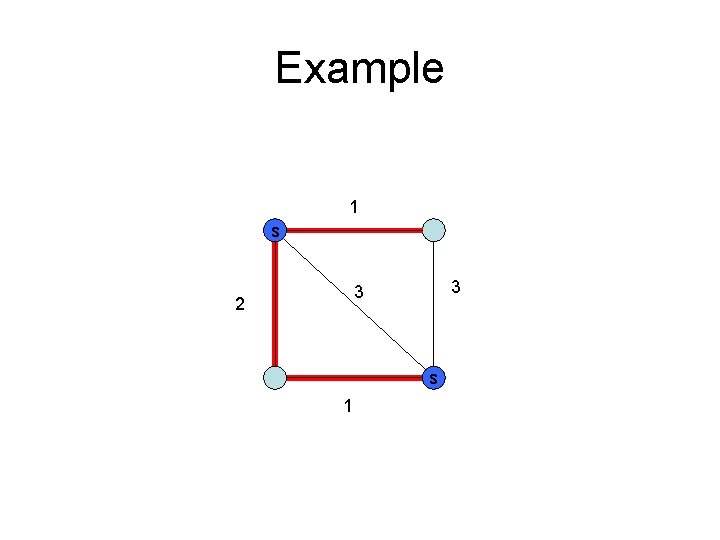
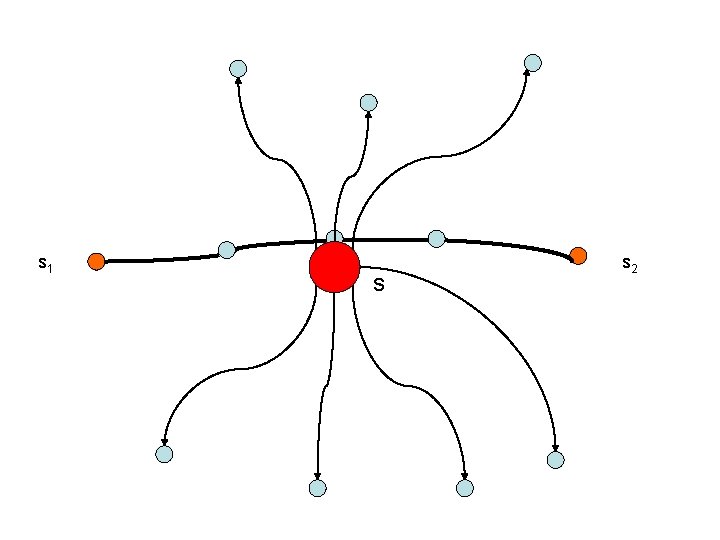
Multi-source Spanning Tree Problems • 在graph上給定k個點, 對這k個點找出到所 有點平均距離最小的spanning tree.

Example 1 s 3 3 2 s 1

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET) NP-complete

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET)

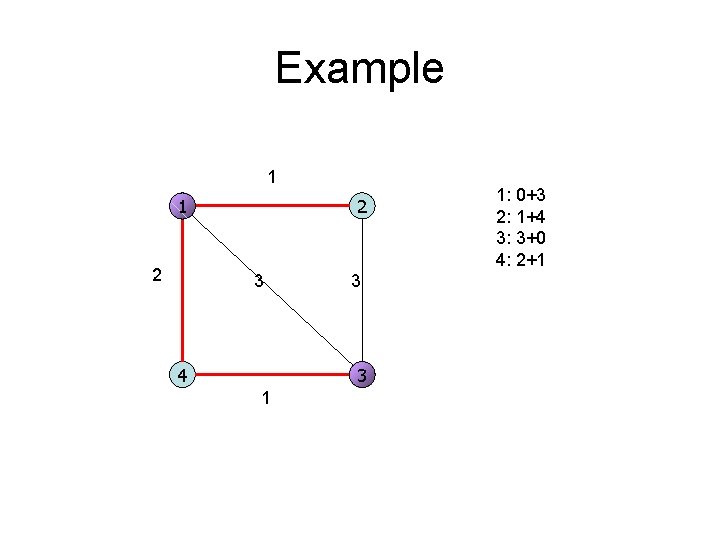
k-MVST • Input: A weighted graph G, k sources ( V(G)), a positive integer K. • Question: Is there a spanning tree T of G such that cost(T) = maxv V s S d. T(s, v) K?

Example 1 2 3 4 3 3 1 1: 0+3 2: 1+4 3: 3+0 4: 2+1

k-MVST NP-complete • 2 -MVST is NP-complete even for graphs with unit edge lengths. • Proof strategy: reduction from 3 -SAT.

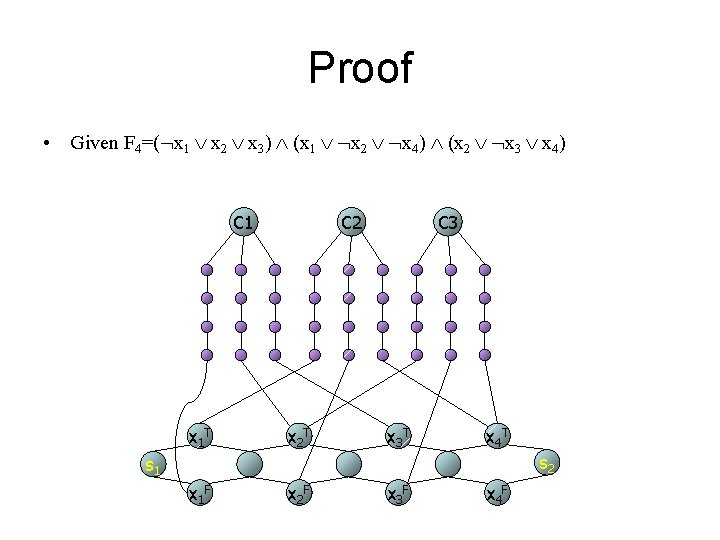
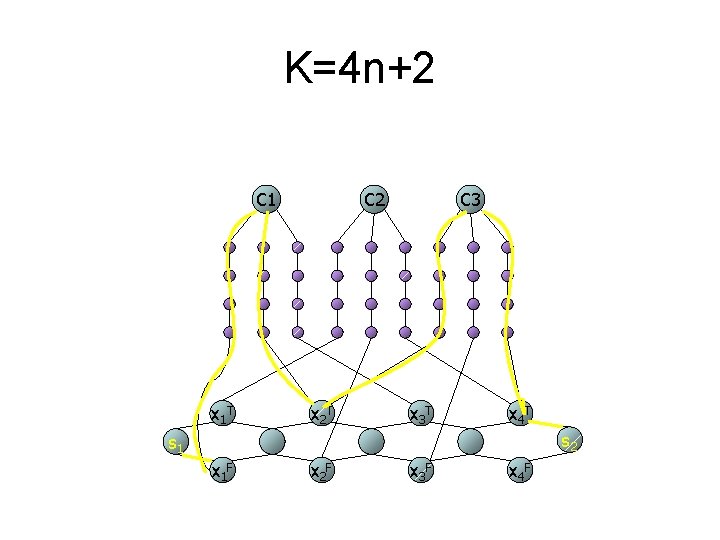
Proof • Given F 4=( x 1 x 2 x 3) (x 1 x 2 x 4) (x 2 x 3 x 4) C 1 x 1 T C 2 x 2 T C 3 x 3 T x 4 T s 2 s 1 x 1 F x 2 F x 3 F x 4 F

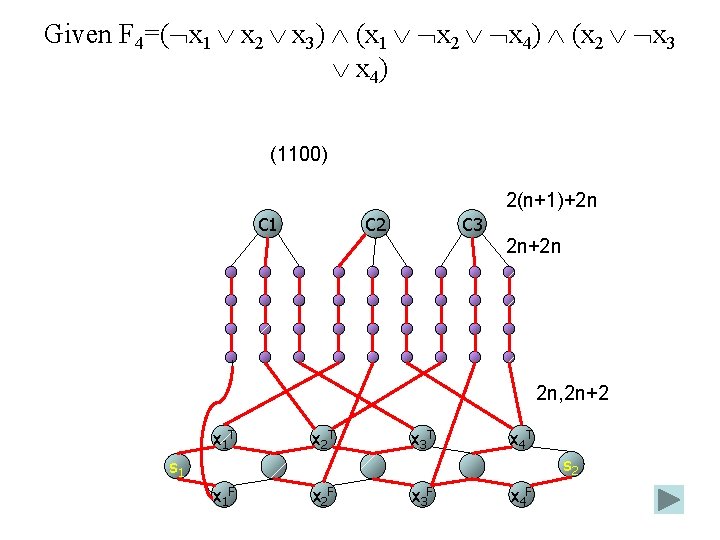
Proof (continue) • Let K=4 n+2, S={s 1, s 2} • (3 -SAT imply T) • (T imply 3 -SAT)

Given F 4=( x 1 x 2 x 3) (x 1 x 2 x 4) (x 2 x 3 x 4) (1100) 2(n+1)+2 n C 1 C 2 C 3 2 n+2 n 2 n, 2 n+2 x 1 T x 2 T x 3 T x 4 T s 2 s 1 x 1 F x 2 F x 3 F x 4 F

Proof (continue) • 若找到一T使得cost(T) K, 則(s 1, s 2)-path 即為所求之assignment • Claim 1: (s 1, s 2)-path 僅由variable node 構 成 • Claim 2: 此path 為所求之truth assignment

K=4 n+2 C 1 x 1 T C 2 x 2 T C 3 x 3 T x 4 T s 2 s 1 x 1 F x 2 F x 3 F x 4 F

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET)

k-source Shortest Path Spanning Tree • Instance: A graph G=(V, E) with the length function l, k source s 1, …, sk V , a positive integer R • Question : Is there a spanning tree T of G whose cost does not exceed R?

Cost Metric • Cost of spanning tree T is defined to be sum of routing costs from all source nodes to other nodes

s 1 s 2

k=1 • This problem becomes single source shortest path problem, with well known efficient solutions (e. x. the Dijkstra-Prim algorithm)

k=n • Minimum Routing Cost spanning Tree • NP • Approximation ratio

We want to show… • 1<k<n • The 2 -SPST problem is NP-complete even in the uniform edge lengths case

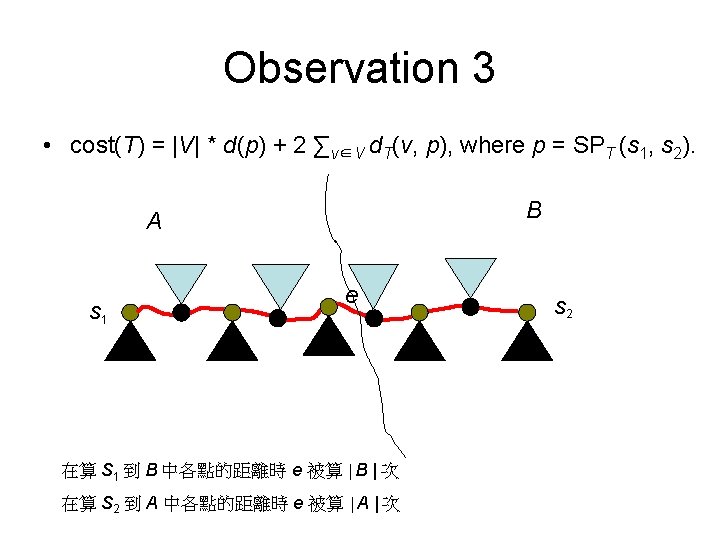
Observation • The cost of a spanning tree with two sources s 1, s 2 is equal to N*d(p)+2* v Vd(v, p) p is the unique path between s 1 and s 2

s 1 s 2

Proof • Use 3 -SAT decision problem to reduce to 2 -SPST problem

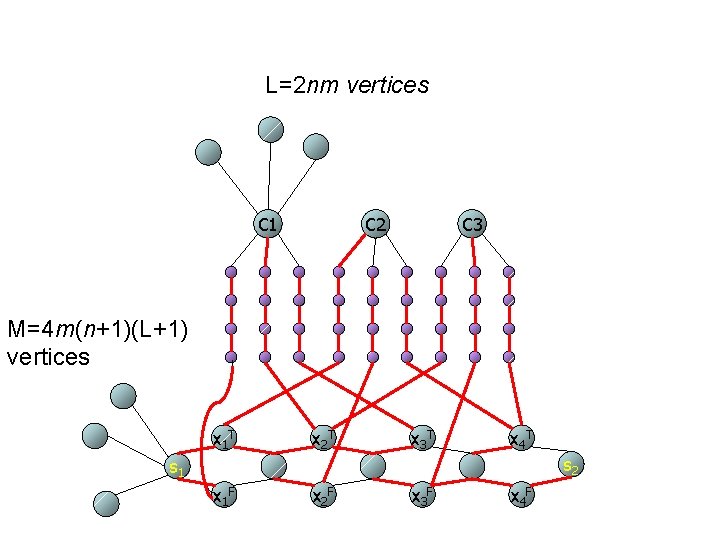
• Given an instance C 1, …, Cm of 3 -SAT. Construct an instance of 2 -SPST by combining following “gadgets”: • A gadget corresponding to the variable xi consist a four-cycle (xi’, xi. T, xi’’, xi. F) • A gadget corresponding a clause Cj=(yj 1, yj 2, yj 3) consists of a vertex labeled ci, adjacent to L=2 nm degree-1 vertices

• Finally, • Length of the path between s 1 and s 2 is at least 2 n • s 1(s 2) is adjacent to M=4 m(n+1)(L+1) degree-1 vertices • This Graph has N=M+3 n+1+Lm+3 nm-2 m • The constant R of 2 -SPST is defined to be 2 n. N+2 M+2 n+m(n+1)(2 L+3 n)-4 m

L=2 nm vertices C 1 C 2 C 3 M=4 m(n+1)(L+1) vertices x 1 T x 2 T x 3 T x 4 T s 2 s 1 x 1 F x 2 F x 3 F x 4 F

By Observation N*d(p)+2* v Vd(v, p) • • The component 2* v Vd(v, p) equals 0 for v on the path p 2 M for M degree-1 vertices 2 n for n non-essential variable 2 nm for m clause vertices 2 Lm(n+1) for m. L degree-1 vertices P(n(n+1)-2) for vertices v in long path (3 m-P)(n-1)n for vertices v in short path

If the instance of 3 -SAT is satisfiable • 2 n. M+2 M+2 n+2 Lm(n+1)+3 n 2 m-nm+2 P(n-1) R

Otherwise… • N+(2 n+2)+2 M >2 Nn+4 M 2 Nn+2 M+8 m(n+1)(L+1) 2 Nn+2 M+2 Lm(n+1)+6 Lm(n+1)+8 m(n+1) 2 Nn+2 M+2 Lm(n+1)+3 nm(n+1)+2 n >R

Corollary • The 2 -SPST problem is NP-complete • The k-SPST problem is NP-complete for any k>1

PTAS for 2 -SPST • Wu, B. Y. , (2002), “A polynomial time approximation scheme for the two-source minimum routing cost spanning trees”, Journal of Algorithms, vol. 44(2), pp. 359378, [SCI, EI] (NSC 91 -2213 -E-366 -004).

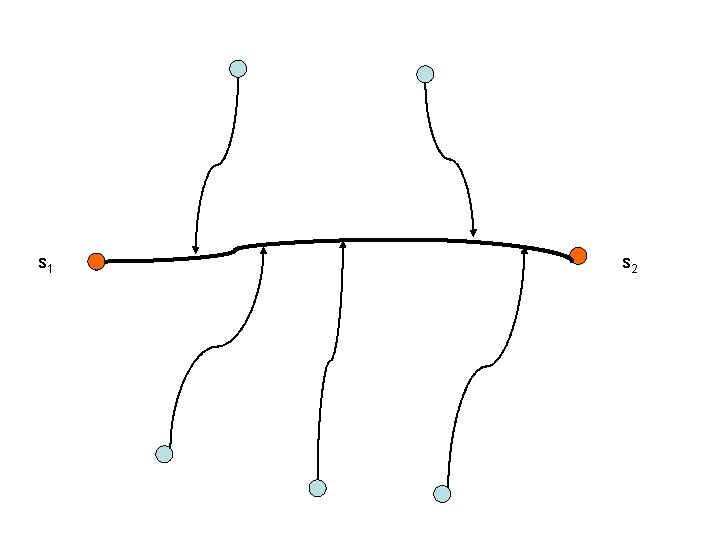
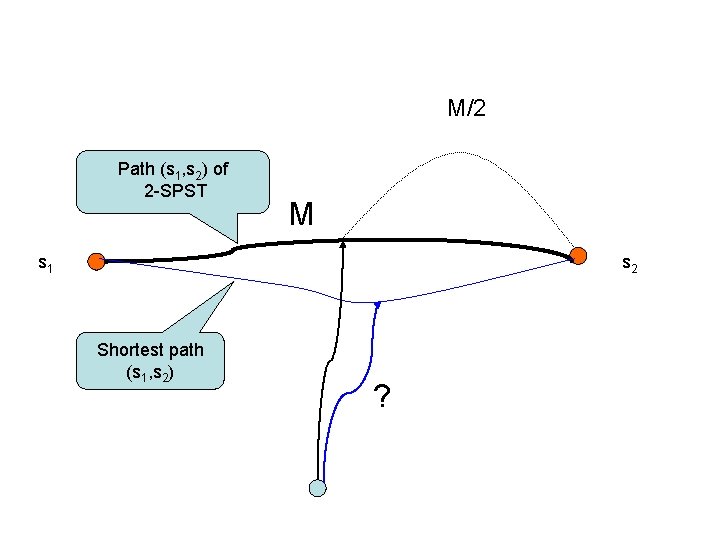
2 -Approximation algorithm for 2 -SPST • Construct shortest path p between s 1, s 2 • Contract all nodes and edges in the path p (include s 1, s 2) to a super node s • Construct single source shortest path tree with source s

s 1 s s 2

Claim • Spanning tree from this algorithm (consist of the shortest path p* between s 1 and s 2) is 2 -approximation of 2 -SPST

M/2 Path (s 1, s 2) of 2 -SPST M s 1 s 2 Shortest path (s 1, s 2) ?

• Any vertex v of G is at most M/2 further away from p than p* • For all vertices in T, we over-estimate the cost of T* by at most 2 n*(M/2)=Mn N*d(p)+2* v Vd(v, p)

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET)

2 -source Maximum Source Shortest paths Spanning Tree (2 - MSST) • Instance: A graph G = (V, E) with unit edge length, 2 sources S = {s 1, s 2} ⊆ V, a positive integer K. • Question: Is there a spanning tree T of G such that max_cost(T) = maxs∈S ∑v∈V d. T(s, v ) ≤ K ?

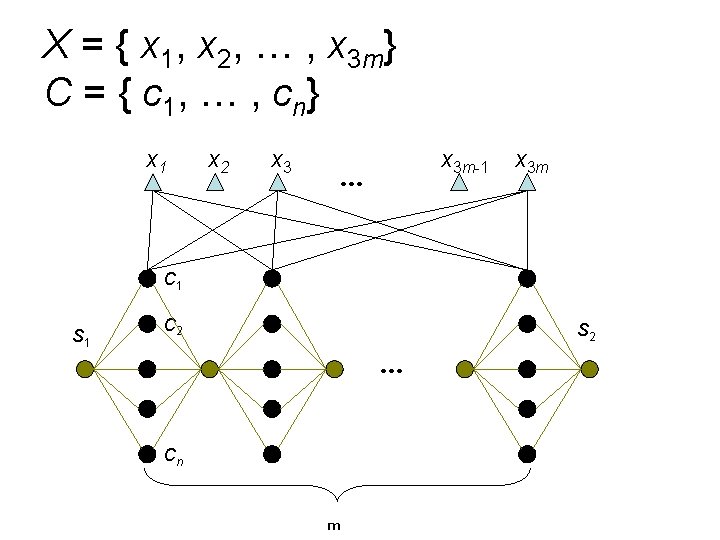
e. Xact 3 -sets Cover (X 3 C) • Instance: A set X with |X| = 3 m and a collection C of 3 -elemet subsets of X. • Question: Is there a C’ ⊆ C such that every member of X occurs in exact one member of C’?

Reduce X 3 C to 2 -MSST • Input: An X 3 C instance (X , C). • Output: A 2 -MSST instance (G, S, K) such that (X, C) has an exact cover (G, S, K) has a 2 MSST.

The ⇒ direction • Input: An X 3 C instance (X, C). • Output: A 2 -MSST instance (G, S, K) such that (X, C) has an exact cover ⇒ G has a spanning tree T with max_cost(T) ≤ K.

X = { x 1, x 2, … , x 3 m} C = { c 1, … , cn} x 1 x 2 x 3 m-1 … x 3 m C 1 S 1 C 2 S 2 … Cn m

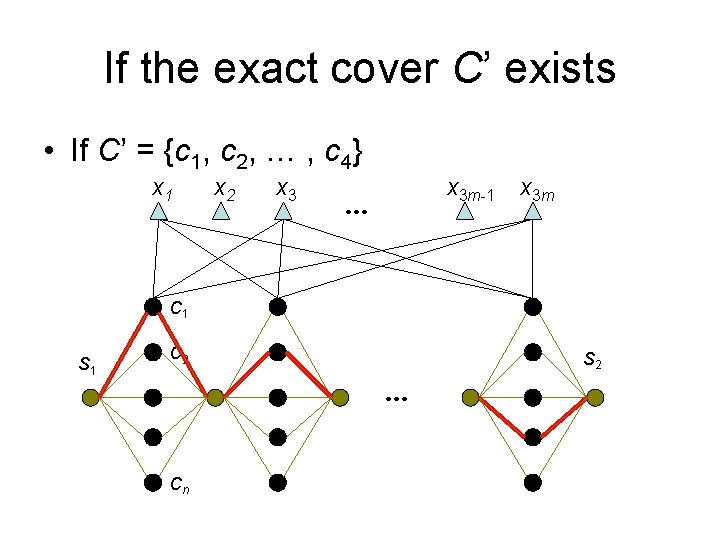
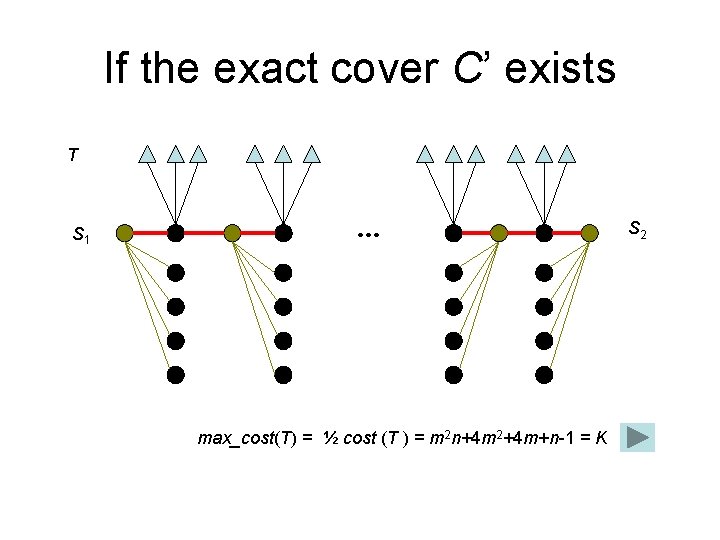
If the exact cover C’ exists • If C’ = {c 1, c 2, … , c 4} x 1 x 2 x 3 m-1 … x 3 m C 1 S 1 C 2 S 2 … Cn

If the exact cover C’ exists T S 1 … max_cost(T) = ½ cost (T ) = m 2 n+4 m 2+4 m+n-1 = K S 2

The ⇐ direction • Input: An X 3 C instance (X, C). • Output: A 2 -MSST instance (G, S, K) such that (X, C) has an exact cover ⇐ G has a spanning tree T with max_cost(T) ≤ K

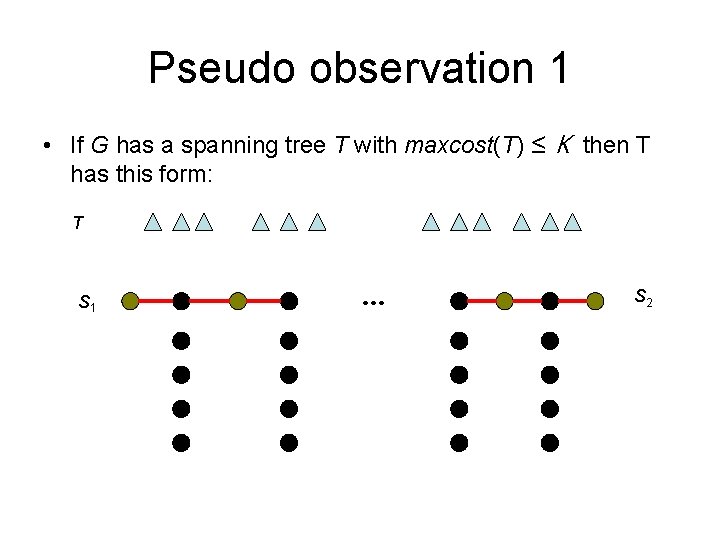
Pseudo proof If G has a spanning tree T with max_cost(T) ≤ K then (X, C) has an exact cover Lemma 1 Pseudo observation 1 Observation 2 Observation 3

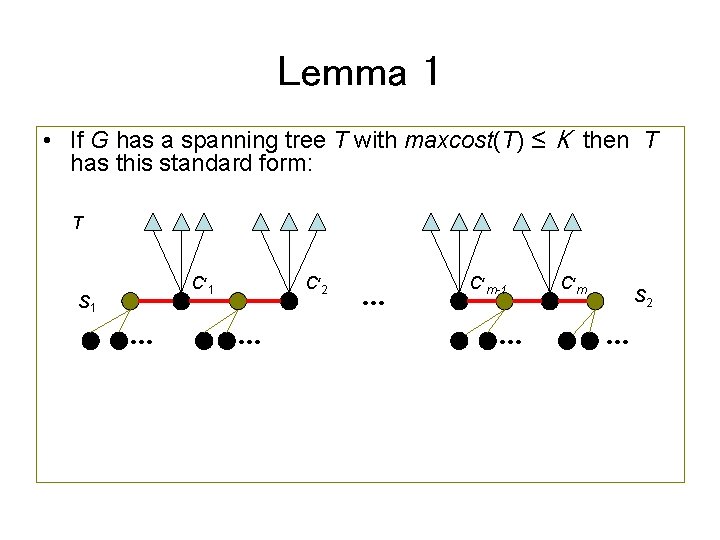
Lemma 1 • If G has a spanning tree T with maxcost(T) ≤ K then T has this standard form: T C’ 1 S 1 … C’ 2 … … C’m-1 … C’m S 2 …

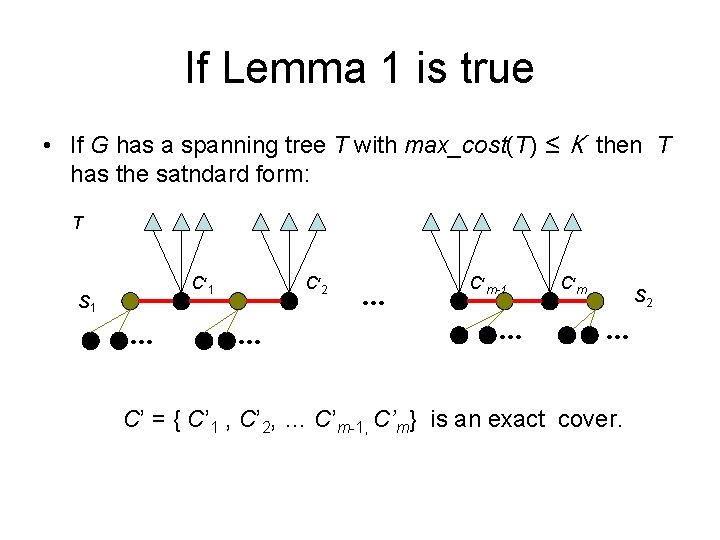
If Lemma 1 is true • If G has a spanning tree T with max_cost(T) ≤ K then T has the satndard form: T C’ 1 S 1 … C’ 2 … … C’m-1 … C’m S 2 … C’ = { C’ 1 , C’ 2, … C’m-1, C’m} is an exact cover.

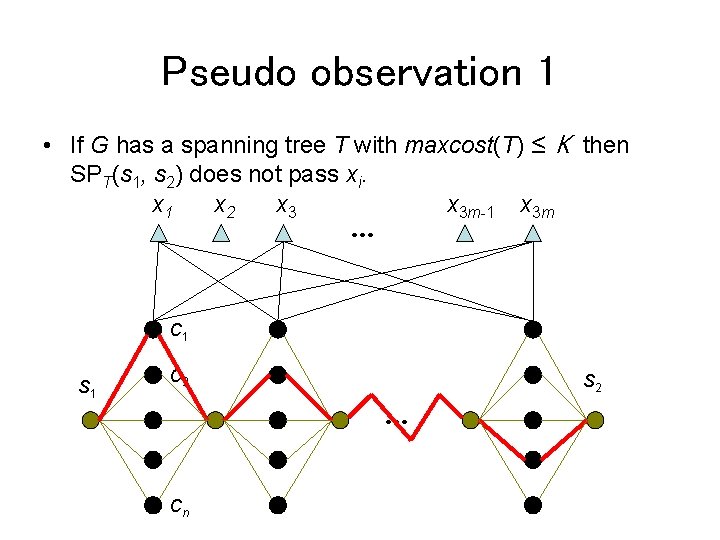
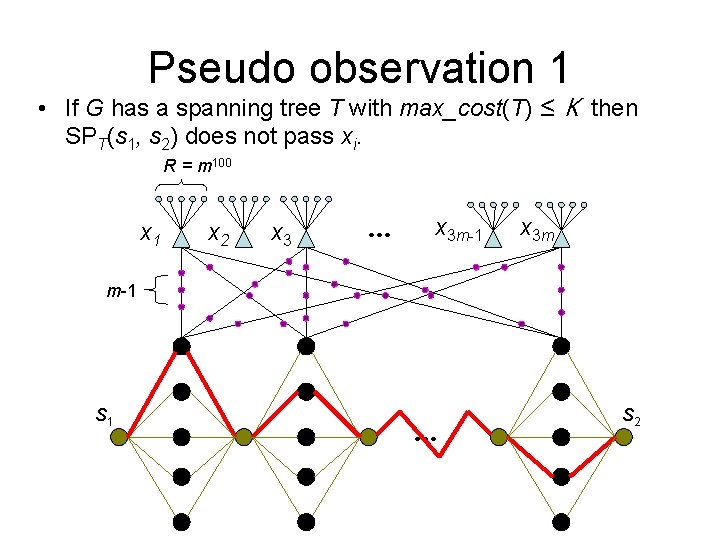
Pseudo observation 1 • If G has a spanning tree T with maxcost(T) ≤ K then SPT(s 1, s 2) does not pass xi. x 1 x 2 x 3 m-1 x 3 m … C 1 S 1 C 2 S 2 … Cn

Pseudo observation 1 • If G has a spanning tree T with maxcost(T) ≤ K then T has this form: T S 1 … S 2

Observation 2 • max_cost(T) ≥ ½ cost(T) where cost(T) = ∑s∈S ∑v∈V d. T(s, v ). • So cost(T) has to be smaller than 2 k.

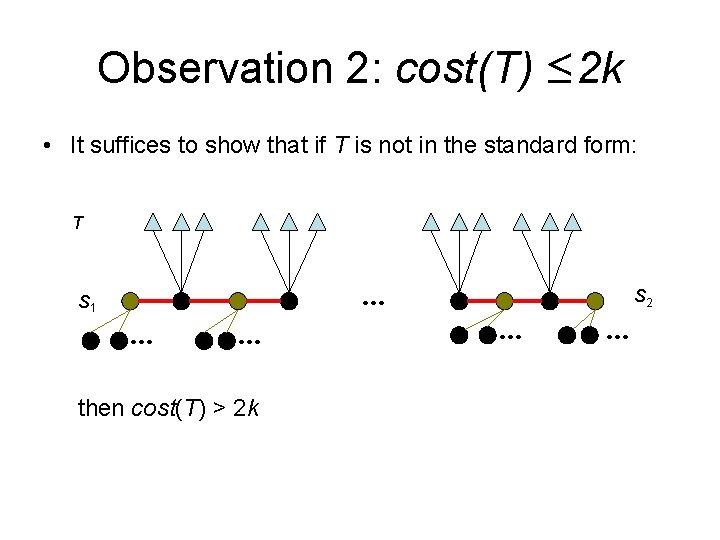
Observation 2: cost(T) ≤ 2 k • It suffices to show that if T is not in the standard form: T S 1 … … then cost(T) > 2 k … S 2 … …

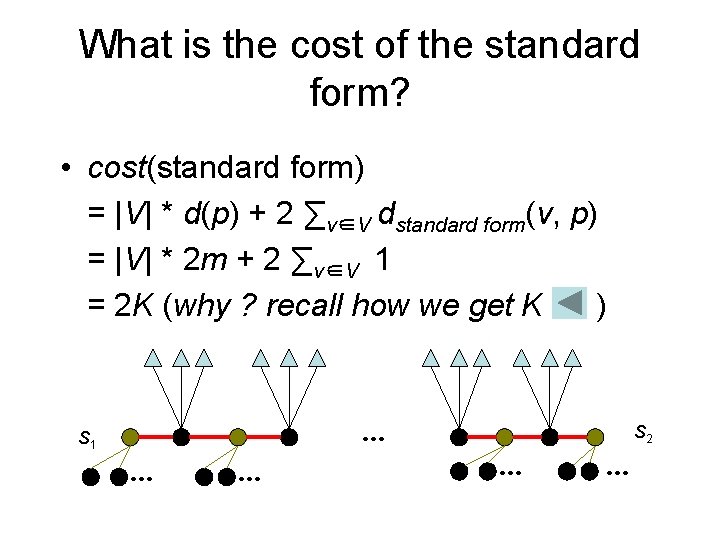
What is the cost of the standard form? • cost(standard form) = |V| * d(p) + 2 ∑v∈V dstandard form(v, p) = |V| * 2 m + 2 ∑v∈V 1 = 2 K (why ? recall how we get K ) S 1 … … … S 2 … …

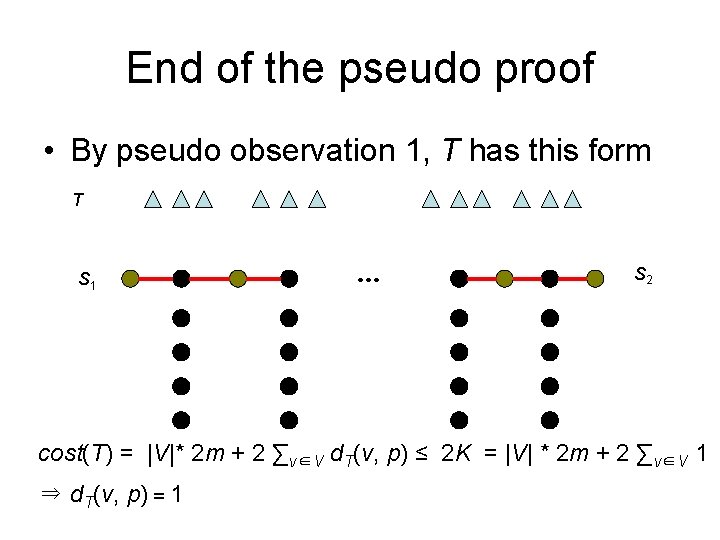
End of the pseudo proof • By pseudo observation 1, T has this form T S 1 … S 2 cost(T) = |V|* 2 m + 2 ∑v∈V d. T(v, p) ≤ 2 K = |V| * 2 m + 2 ∑v∈V 1 ⇒ d. T(v, p) = 1

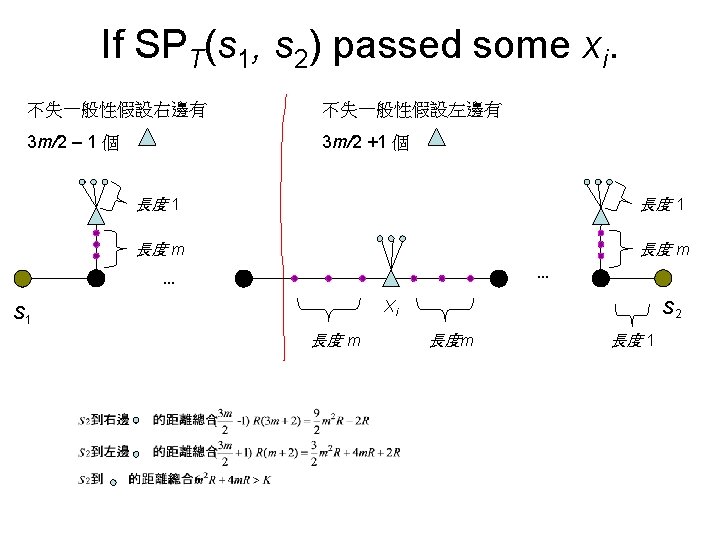
Pseudo observation 1 • If G has a spanning tree T with max_cost(T) ≤ K then SPT(s 1, s 2) does not pass xi. R = m 100 x 1 x 2 x 3 … x 3 m-1 x 3 m m-1 S 1 … S 2

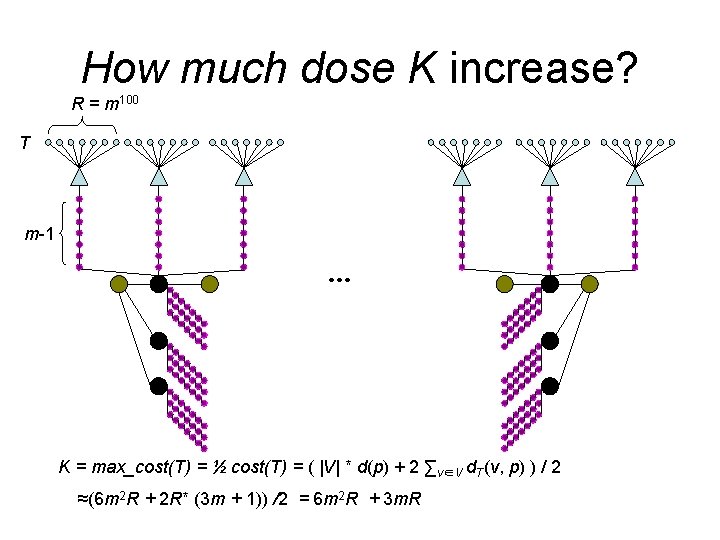
How much dose K increase? R = m 100 T m-1 … K = max_cost(T) = ½ cost(T) = ( |V| * d(p) + 2 ∑v∈V d. T(v, p) ) / 2 ≈(6 m 2 R + 2 R* (3 m + 1)) /2 = 6 m 2 R + 3 m. R

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET)

k-SVET Problem • Instance: A graph G = (V, E) with a length function l, k sources S = {s 1, …, sk} V, a positive integer K. • Question: Is there a spanning tree T of G such that cost = max d. T(s, v) K?

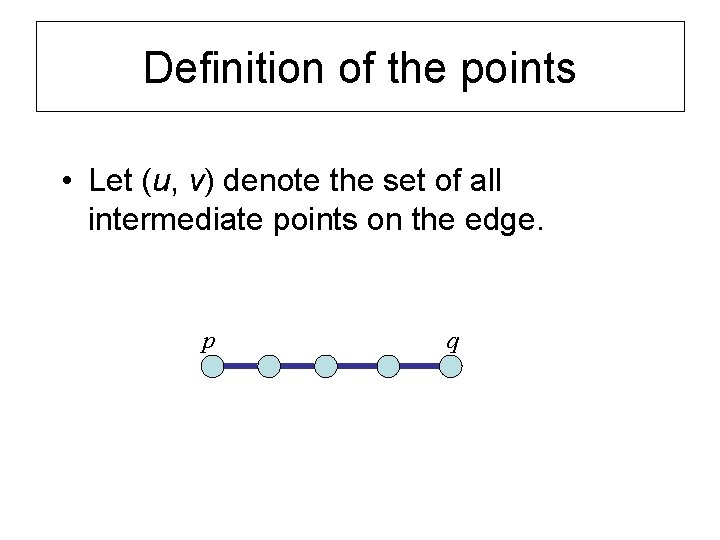
Definition of the points • Let (u, v) denote the set of all intermediate points on the edge. p q

Cont’d • Let dp(γv) be the distance along the edge(p, q) from p to γv. • dp(γv) = ½(d. G(q, v) – d. G(p, v) + l(p, q)) v ∵b = c + d – a = (l(p, q) – b) + d – a ∴b = ½(l(p, q) + d – a) d a γv p b q c

Cont’d • dp(γv 1) dp(γv 2) … dp(γvn) • γv 1 = vn = p and γvn = v 1 = q p γv 1 q γv 2 … … γvn

Theorem 3. 1 • For any two points x and y in the interval (γvi, γvi+1), the set of SPSTs rooted at x is the same as the set of SPSTs rooted at y.

Theorem 3. 2 • Any SPST for a point in the interval(γvi-1, γvi+1) is also a SPST for the point γvi

Strategy • The key strategy for proving that such minimum spanning tree problem has an efficient solution is to prove that a single source shortest paths spanning tree (SPST) from some points is optimal for the given cost metric.

Cont’d • B. Mc. Mahan and A. Proskurowski. Multi-source spanning trees: Algorithms for minimizing source eccentricities. Submitted, 1999. • R. Ravi, R. Sundaram, M. V. Marathe, D. J. Rosenkrantz, and S. S. Ravi. Spanning trees – short or small. SIAM Journal of Discrete Mathematics, 9(2): 178– 200, 1996.

Critical • Defien a vertex to be critical for a source if it is at the maximum distance from the source. • Likewise, a source is critical for a vertex if it is the source at maximum distance from the vertex. Note that these are not necessarily unique.

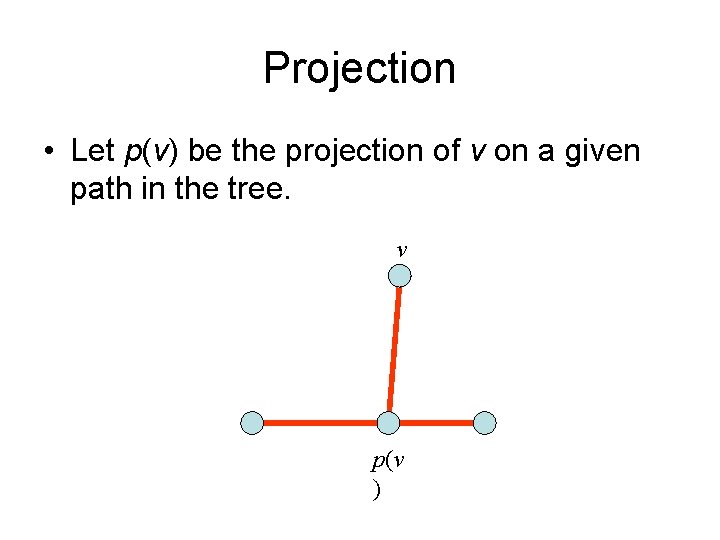
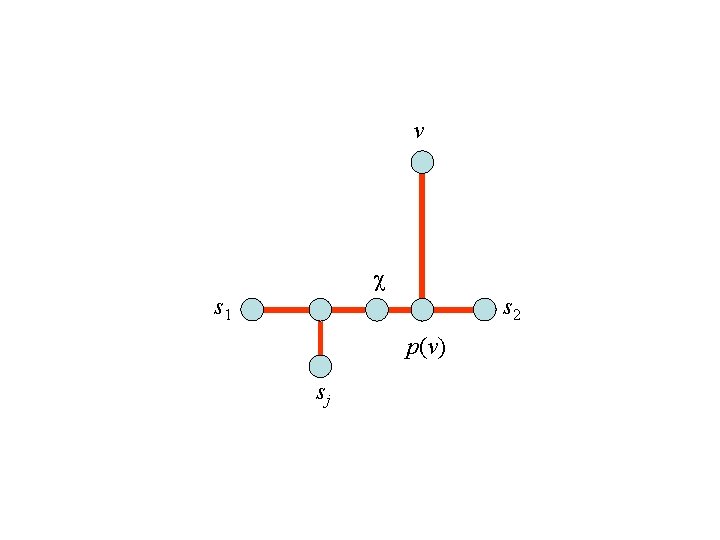
Projection • Let p(v) be the projection of v on a given path in the tree. v p(v )

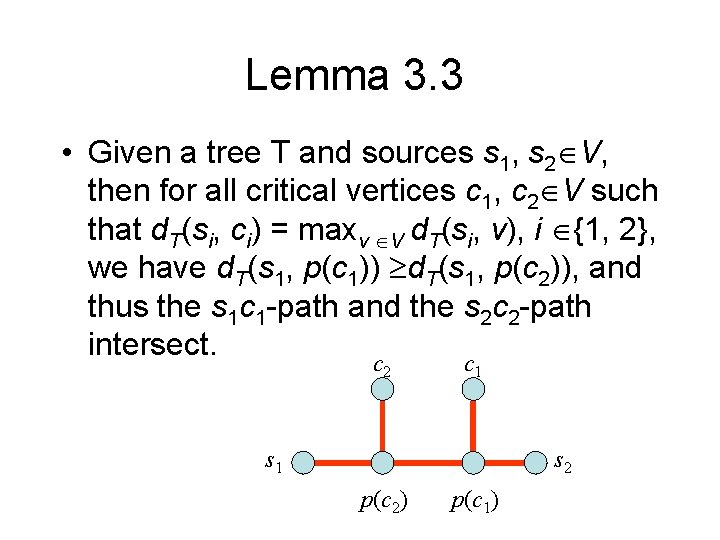
Lemma 3. 3 • Given a tree T and sources s 1, s 2 V, then for all critical vertices c 1, c 2 V such that d. T(si, ci) = maxv V d. T(si, v), i {1, 2}, we have d. T(s 1, p(c 1)) d. T(s 1, p(c 2)), and thus the s 1 c 1 -path and the s 2 c 2 -path intersect. c c 2 1 s 2 p(c 2) p(c 1)

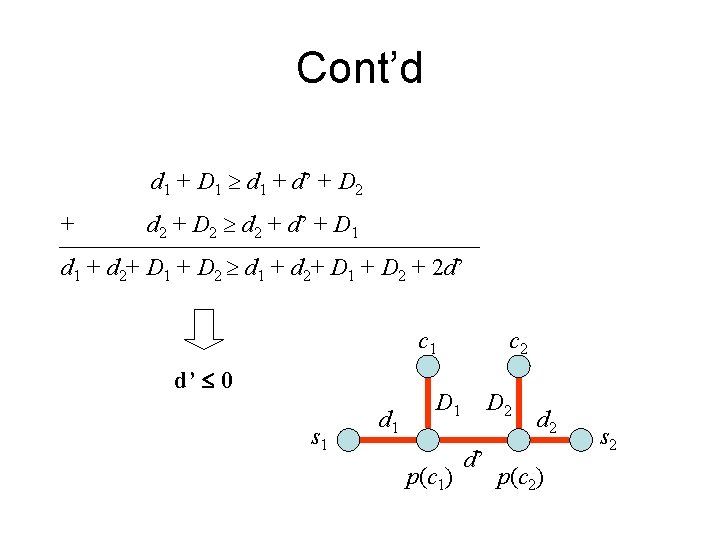
Cont’d d 1 + D 1 d 1 + d’ + D 2 + d 2 + D 2 d 2 + d’ + D 1 d 1 + d 2+ D 1 + D 2 + 2 d’ c 1 d’ 0 s 1 d 1 c 2 D 1 p(c 1) D 2 d’ d 2 p(c 2) s 2

Lemma 3. 4 • Given a tree T, let s 1 and s 2 be two sources with maximum intrasource distance, and let be the midpoint of the s 1 s 2 -path in T. For all vertices v V(T), the path in T from v to its critical source must include .

Lemma 3. 5 • Let s 1 and s 2 be two sources with maximum intrasource distance in a tree T, and pick to be the midpoint on the s 1 s 2 path in T. For any vertex v and any source si, i = 3, …, k, either d. T(v, s 1) d. T(v, si) or d. T(v, s 2) d. T(v, si).

v s 1 s 2 p(v) sj

Theorem 3. 6 • Given a graph G with sources s 1, …, sk V(G), there exists a point such that any SPST rooted at is an optimal tree for k-SVET.

Cont’d • Let T* be an optimal tree for k-SVET and s 1 and s 2 be two sources with maximum intrasource distance in T*. • Pick to be the midpoint on the s 1 s 2 -path in T*. Let T be a shortest paths spanning tree of G with the root and assume cost (T*) < cost (T ).

Cont’d • There exists some vertex v and a critical source sj for v such that d. T*(v, si) < d. T (v, sj).

Cont’d • • • Without lost of generality, assume i = 1. d. T*(v, s 1) = d. T*(v, ) + d. T*( , s 1) d. T (v, sj) d. T (v, ) + d. T ( , sj) d. T*(v, ) + d. T*( , s 1) < d. T (v, ) + d. T ( , sj) d. T*( , s 1) d. T*( , sj) d. T*(v, ) + d. T*( , sj) < d. T (v, ) + d. T ( , sj)

Cont’d • Therefore, cost (T*) = cost (T ). • So a SPST rooted at is optimal for k. SVET.

Outline • k-Source Maximum Vertex Shortest Paths Spanning Tree (k-MVST) • k-Source Spanning Tree Problems (k-SPST) • k-Source Maximum Source Shortest Paths Spanning Tree (k-MSST) • k-Source Sum of Vertex Eccentricities Spanning Tree (k-SVET) • k-Source Sum of Source Eccentricities Spanning Tree (k-SSET)

k-Source Sum of Source Eccentricities Spanning Tree (k-SSET) • Instance: A graph with a length function, , k sources a positive integer K. , • Question: Is there a spanning tree T of G such that

eccentricity, diameter, diametral • The eccentricity of a vertex v is defined as the distance from v to the most distant vertex from v, i. e or. • The maximum eccentricity among all the vertices of G is called the diameter of G, in other words, the diameter is the longest distance between any two vertices in the graph, and a shortest path of this length is called diametral.

k-SSET • Lemma 3. 8 In a tree T, let be the midpoint of a diametral path with x and y the endpoints of this graph. For each source si and its critical vertex ci, is on the sici-path in T. Moreover, if Ci is the set of critical vertices for si, then

Lemma 3. 8 • Proof. First, show the xy-path intersects with the sici-path for some i. 1. Because xy-path is diametral, so f h + b, otherwise xci-path would be If the two paths do not intersect, they must be joined in T by longer than the sici-path. some non-empty path η sharing a vertex u with the sici-path andba vertex with the xy-path 2. Also h + f , votherwise the siy-path woule be longer than the sici-path. These two facts imply h 0, and thus the xy-path must intersect the sici-path

Lemma 3. 8 • Proof. The next step is to show η : intersection of the xy-path and sici-path u, v: endpoints of η q : the diameter of T, q = d. T(x, y), xy -path : a diametral path of T ci Ci, b f, and xy-path is a diametral of T, f b b = f d. T(si, y) = d. T(si, ci) y Ci

Lemma 3. 8 • Proof. Finally, let be the midpoint of the xy-path, so d. T(x, ) = d. T(y, ) = q. Show that lies in η and thus on the If η, then e q or f > q sici-path. 1. e q, then h+f < q so e > h+b and a+e > a+h+b, contradiction. 2. f > q, then b> q which implies b+f > q, contradiction. e, f q, so η, and thus is on the sici-path.

Theorem 3. 9. • Given graph G with sources S and a tree T* minimizing cost 5 over all spanning trees of G. A SPST rooted at , the midpoint of a diametral path of T*, is also optimal for k-SSET. • Proof. Let T* : an optimal tree q : the diameter of T *, x, y: endpoints of a diametral path

Theorem 3. 9. • Proof. By Lemma 3. 8, all sici-paths include , and x or y is critical for each source. Let Tx be a SPST rooted at . Let ci be a critical vertex for si in T* and a critical vertex for si in Tx. Then

k-SSET • From Theorem 3. 9, 3. 1 and 3. 2, Theorem 3. 10. follows directly. k-SSET