COMPLEXITY THEORY FOUNDATIONS COMPLEXITY THEORY FOUNDATIONS COMPLEXITY THEORY

COMPLEXITY THEORY: FOUNDATIONS

COMPLEXITY THEORY: FOUNDATIONS

COMPLEXITY THEORY: FOUNDATIONS

COMPLEXITY THEORY: FOUNDATIONS

COMPLEXITY THEORY: FOUNDATIONS Þ We attempt to show that: - one problem is harder than another by showing that: the best possible algorithm for solving the former requires more time, space, or other resources than the best possible algorithm to solve the latter. OR that all members of a class of problems are of equal difficulty, at least with regard to their asymptotic behavior.

6. 1 REDUCTIONS In chapter 5 we saw that: reductions among sets provide a tool for studying computability. - To study complexity – need to define reductions among problems and to assess or bound the cost of each reduction. Eg. 1) Reduce sorting to – computation of convex hulls in linear time. 2) Reduce marriage problem to a special instance of network-flow problem and solve that instance (and vice-versa) => Sorting a set of number and finding the convex-hull of a set of points in 2 D are computationally equivalent to within a linear-time additive term.

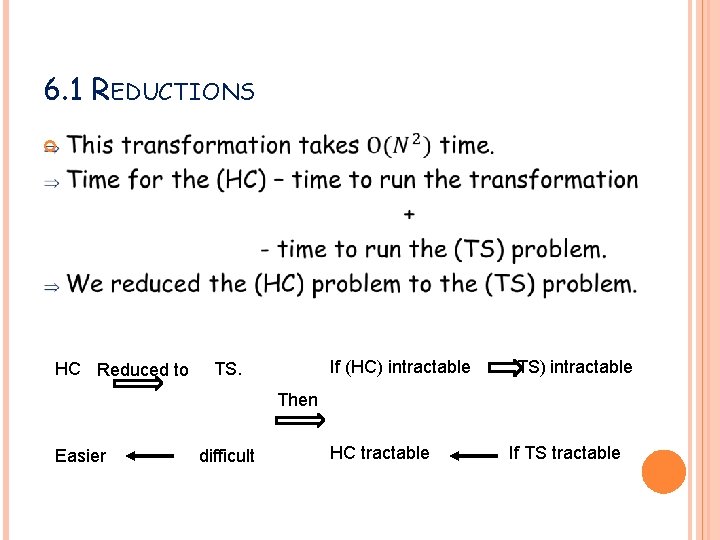
6. 1 REDUCTIONS Example detailed in text: TRAVELING SALESMAN & HAMILTONIAN CIRCUIT - No solution that is guaranteed to run in polynomial time is known for either of these 2 problems (TS & HC) - However - if we discover a polynomial solution for (TS) => We could immediately construct a polynomial solution for (HC).

6. 1 REDUCTIONS Given a particular graph of N vertices: Eg) – we transform this instance of the Hamiltonian circuit problem into an instance of the Travelling Salesman (TS) problem ( by associating each vertex of the graph with a city and setting the distance between 2 cities to are: 1. If the corresponding vertices are connected by all edge and to 2. Otherwise Þ If (TS) returns all optimal tour of N (that is the one corresponding to the Hamiltonian circuit) Þ Does not return N for an optimal tour then no Hamiltonian tour exists. -

6. 1 REDUCTIONS HC Reduced to TS. If (HC) intractable (TS) intractable HC tractable If TS tractable Then Easier difficult

6. 1 REDUCTIONS

6. 1 REDUCTIONS Smallest subsets problem: How many different subsets are there such that the sum of the elements of each subset is no longer than “M” (a positive size bound)? Þ ENUMERATION v We reduce the partition problem (P) to the smallest subsets (SS) problem. - An instance of (P) admits a solution only if the sum of all the sizes is an even number => start computing sum Þ If it is “add ” answer is “no” and stop. Otherwise use procedure to solve smallest subsets with the same set of elements and the same sizes as in the partition problem. Study proof for exam page 173. Read exercise 6. 1, 6. 2.

6. 1 REDUCTIONS

6. 1 REDUCTIONS

6. 1 REDUCTIONS

6. 1 REDUCTIONS We can choose a specific type of reduction: The chosen type establishes a minimum degree of similarity between the two problems: Eg. STRONG similarity {(HC) and (TS) when both are viewed as decision problems. LOOSER similarity { partition vs smallest subsets Important 2 types of reductions : i. Turing (algorithmic reductions) -> apply to any type of problem ii. Many-one reductions (transformations) -> apply only to decision problems. Note: many-one reductions have been applied earlier on sets. Here we use them on decision problems since a decision problem could be viewed as a set of all “yes” instances of the problem.

6. 1 REDUCTIONS

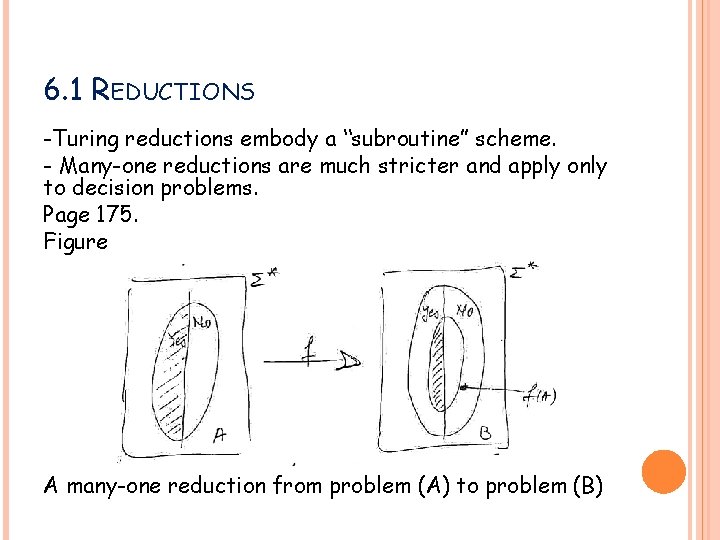
6. 1 REDUCTIONS -Turing reductions embody a “subroutine” scheme. - Many-one reductions are much stricter and apply only to decision problems. Page 175. Figure A many-one reduction from problem (A) to problem (B)

6. 1 REDUCTIONS Discussion on page 175. If “f” mapping is injective => “one-reduction” injective + surjective => the 2 problems are isomorphic. v We need to also qualify the reduction by the allowable amount of resources used in the reduction: - Polynomial-time transformation. - Logarithmic-space Turing reduction Eg. (HC) to (TS) is a polynomial-time transformation partition to smallest subsets is a polynomial-time Turing reduction.

6. 1. 2 REDUCTIONS & COMPLEXITY CLASSES Complexity classes are characterized simply by one or more resource bounds: (D) A complexity class for some model of computation is the set of all decision problems solvable on this model under same given resources bounds. • Each complexity class includes all classes of strictly smaller complexity (i. e. , class of intractable problems includes the class of tractable problems) Note: A complexity class (=> includes problems of wide variety in their difficulty) differs from all equivalence class (=> includes problems of similar difficulty) -

6. 1. 2 REDUCTIONS & COMPLEXITY CLASSES

6. 1. 2 REDUCTIONS & COMPLEXITY CLASSES Any complete problem must reduce to any other. Þ The set of all complete problems for Y forms an equivalence class under “t”, since each complete problem is supposed to be the hardest in Y, and thus no particular complete problem could be harder than any other. - Requiring a problem to be complete for a class is typically a very stringent condition and - not every class has complete problems => - however, complete problems for certain classes are common. v

6. 1. 2 REDUCTIONS & COMPLEXITY CLASSES (S) If complete problems exist for a complexity class under suitable type of reduction (one that uses fewer resources than are available in the class), then they characterize the boundaries of a complexity class as follows: 1) If any one of the complete problems can be solved efficiently then all of the problems in the class can (be solved efficiently) 2) If a new problem can be shown to be strictly more difficult than some complete problem, then the new problem cannot be a member of the complexity class.

6. 1. 2 REDUCTIONS & COMPLEXITY CLASSES