Algorithm Cost Algorithm Complexity Algorithm Cost LB Back

Algorithm Cost Algorithm Complexity

Algorithm Cost

LB Back to Bunnies • Recall that we calculated Fibonacci Numbers using two different techniques – Recursion – Iteration

LB Back to Bunnies • Recursive calculation of Fibonacci Numbers: Fib(1) = 1 Fib(2) = 1 Fib(N) = Fib(N-1) + Fib(N-2) So: Fib(3) = Fib(2) + Fib(1) = 1 + 1 = 2
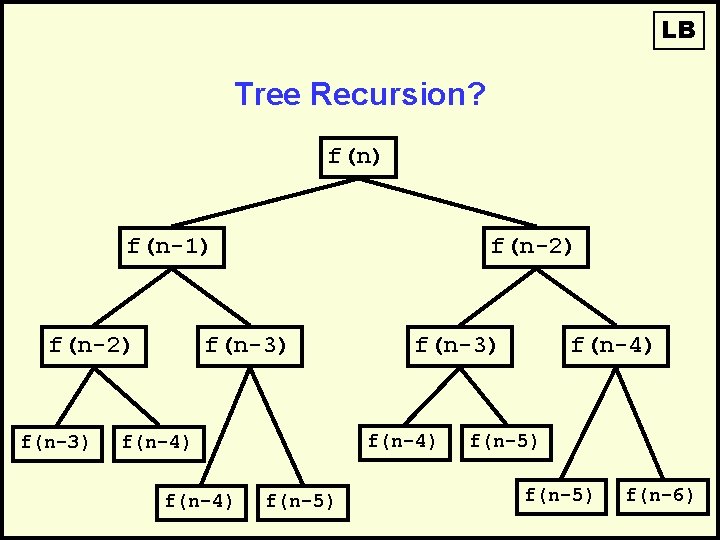
LB Tree Recursion? f(n) f(n-1) f(n-2) f(n-3) f(n-4) f(n-3) f(n-5) f(n-4) f(n-5) f(n-6)
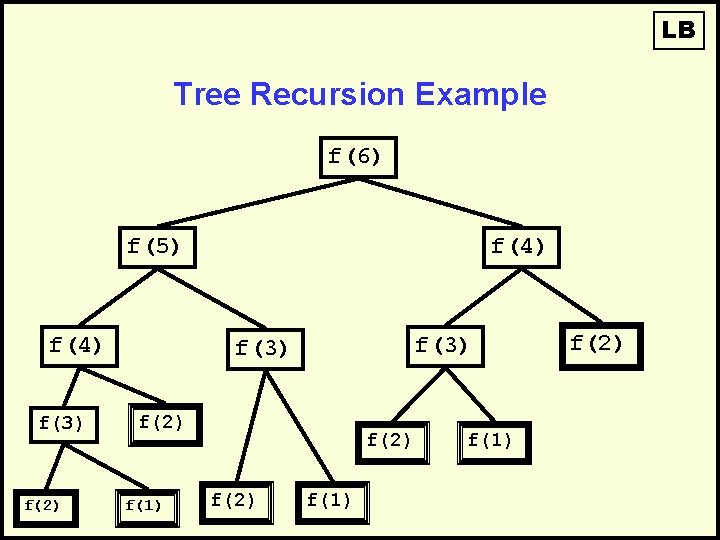
LB Tree Recursion Example f(6) f(5) f(4) f(3) f(2) f(1) f(2)

LB Recursively public static int fib. R(int n) { if(n == 1 || n ==2) return 1; else return fib. R(n-1) + fib. R(n-2); }

LB Iteratively public static int fib. I(int n) { int oldest = 1; int old = 1; int fib = 1; while(n-- > 2) { fib = old + oldest; oldest = old; old = fib; } return fib; }

Slight Modifications LB public static int fib. I(int n) { Add int oldest = 1; Counters int old = 1; int fib = 1; while(n-- > 2) { fib = old + oldest; oldest = old; old = fib; public static int fib. R(int n) } { return fib; if(n == 1 || n ==2) } return 1; else return fib. R(n-1) + fib. R(n-2); }

LB Demo

LB Conclusion Algorithm choice or design can make a big difference!

Correctness is Not Enough • It isn’t sufficient that our algorithms perform the required tasks. • We want them to do so efficiently, making the best use of – Space – Time

Time and Space • Time – Instructions take time. – How fast does the algorithm perform? – What affects its runtime? • Space – Data structures take space. – What kind of data structures can be used? – How does the choice of data structure affect the runtime?

Time vs. Space Very often, we can trade space for time: For example: maintain a collection of students’ with SSN information. – Use an array of a billion elements and have immediate access (better time) – Use an array of 35 elements and have to search (better space)

The Right Balance The best solution uses a reasonable mix of space and time. – Select effective data structures to represent your data model. – Utilize efficient methods on these data structures.

Questions?

Algorithm Complexity

Scenarios • I’ve got two algorithms that accomplish the same task – Which is better? • Given an algorithm, can I determine how long it will take to run? – Input is unknown – Don’t want to trace all possible paths of execution • For different input, can I determine how an algorithm’s runtime changes?

Measuring the Growth of Work While it is possible to measure the work done by an algorithm for a given set of input, we need a way to: – Measure the rate of growth of an algorithm based upon the size of the input – Compare algorithms to determine which is better for the situation

LB Introducing Big O • Will allow us to evaluate algorithms. • Has precise mathematical definition • We will use simplified version in CS 1311 • Caution for the real world: Only tells part of the story! • Used in a sense to put algorithms into families

Why Use Big-O Notation • Used when we only know the asymptotic upper bound. • If you are not guaranteed certain input, then it is a valid upper bound that even the worstcase input will be below. • May often be determined by inspection of an algorithm. • Thus we don’t have to do a proof!

Size of Input • In analyzing rate of growth based upon size of input, we’ll use a variable – For each factor in the size, use a new variable – N is most common… Examples: – A linked list of N elements – A 2 D array of N x M elements – A Binary Search Tree of P elements

Formal Definition For a given function g(n), O(g(n)) is defined to be the set of functions O(g(n)) = {f(n) : there exist positive constants c and n 0 such that 0 f(n) cg(n) for all n n 0}
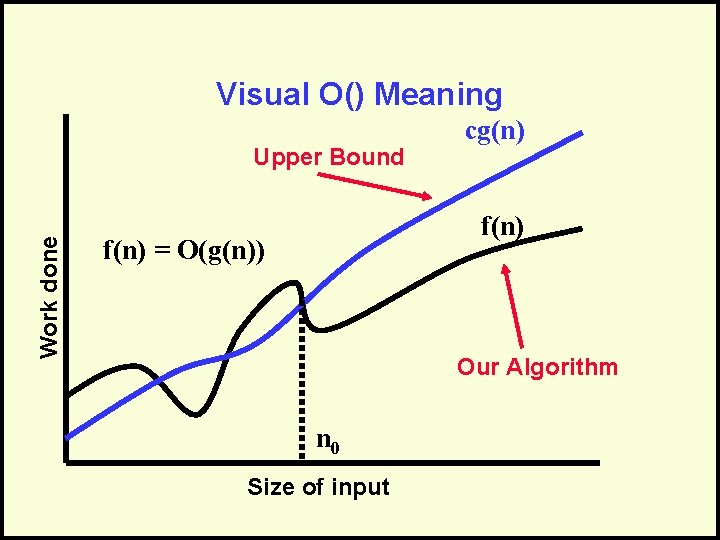
Visual O() Meaning Work done Upper Bound cg(n) f(n) = O(g(n)) Our Algorithm n 0 Size of input

Simplifying O() Answers (Throw-Away Math!) We say 3 n 2 + 2 = O(n 2) drop constants! because we can show that there is a n 0 and a c such that: 0 3 n 2 + 2 cn 2 for n n 0 i. e. c = 4 and n 0 = 2 yields: 0 3 n 2 + 2 4 n 2 for n 2

Correct but Meaningless You could say 3 n 2 + 2 = O(n 6) or 3 n 2 + 2 = O(n 7) But this is like answering: • What’s the world record for the mile? – Less than 3 days. • How long does it take to drive to Chicago? – Less than 11 years.

Comparing Algorithms • Now that we know the formal definition of O() notation (and what it means)… • If we can determine the O() of algorithms… • This establishes the worst they perform. • Thus now we can compare them and see which has the “better” performance.
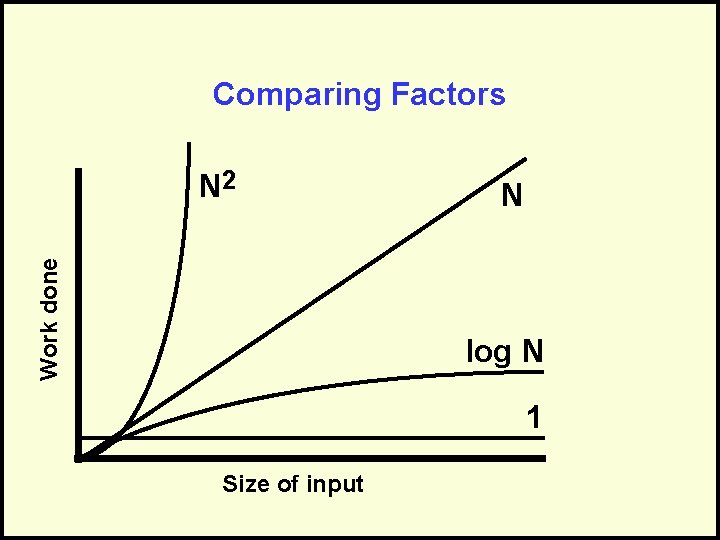
Comparing Factors Work done N 2 N log N 1 Size of input

Correctly Interpreting O() O(1) or “Order One” – Does not mean that it takes only one operation – Does mean that the work doesn’t change as N changes – Is notation for “constant work” O(N) or “Order N” – Does not mean that it takes N operations – Does mean that the work changes in a way that is proportional to N – Is a notation for “work grows at a linear rate”

Complex/Combined Factors • Algorithms typically consist of a sequence of logical steps/sections • We need a way to analyze these more complex algorithms… • It’s easy – analyze the sections and then combine them!
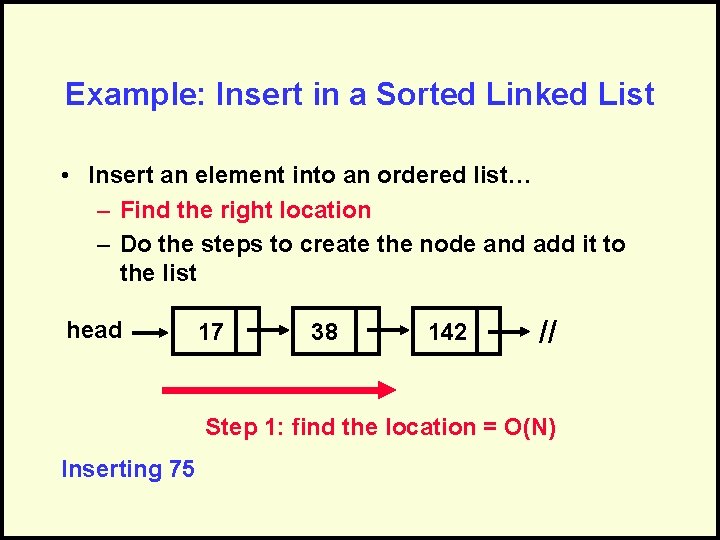
Example: Insert in a Sorted Linked List • Insert an element into an ordered list… – Find the right location – Do the steps to create the node and add it to the list head 17 38 142 // Step 1: find the location = O(N) Inserting 75
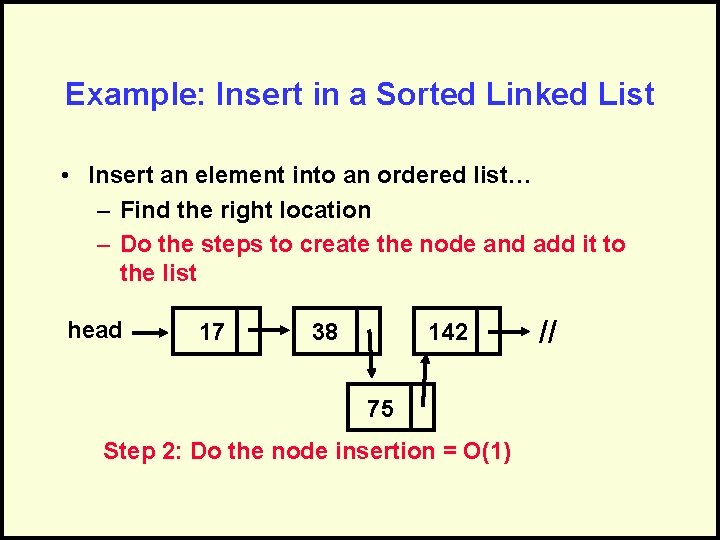
Example: Insert in a Sorted Linked List • Insert an element into an ordered list… – Find the right location – Do the steps to create the node and add it to the list head 17 38 142 75 Step 2: Do the node insertion = O(1) //

Combine the Analysis • Find the right location = O(N) • Insert Node = O(1) • Sequential, so add: – O(N) + O(1) = O(N + 1) = O(N) Only keep dominant factor
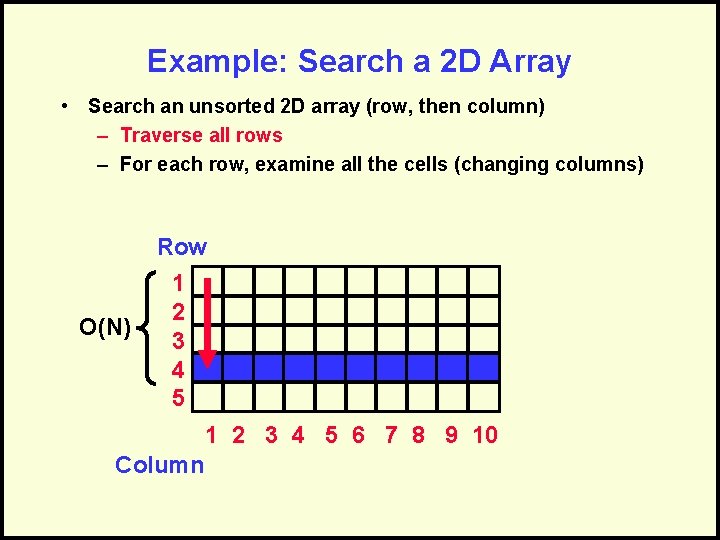
Example: Search a 2 D Array • Search an unsorted 2 D array (row, then column) – Traverse all rows – For each row, examine all the cells (changing columns) Row O(N) 1 2 3 4 5 6 7 8 9 10 Column
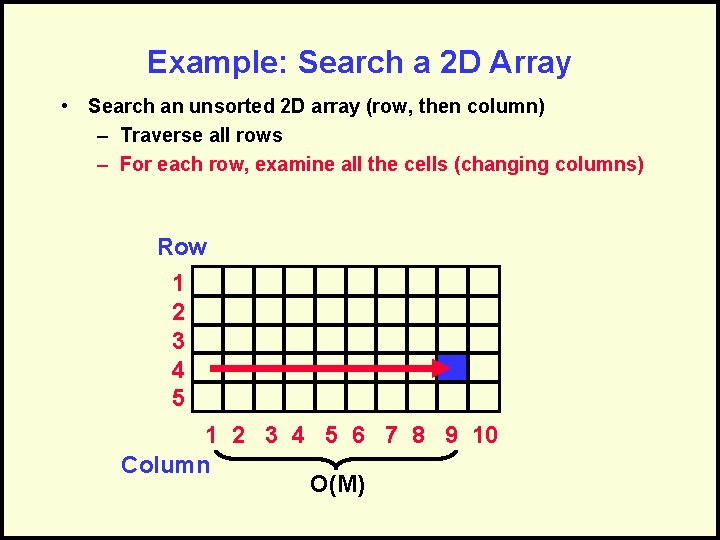
Example: Search a 2 D Array • Search an unsorted 2 D array (row, then column) – Traverse all rows – For each row, examine all the cells (changing columns) Row 1 2 3 4 5 6 7 8 9 10 Column O(M)

Combine the Analysis • Traverse rows = O(N) – Examine all cells in row = O(M) • Embedded, so multiply: – O(N) x O(M) = O(N*M)
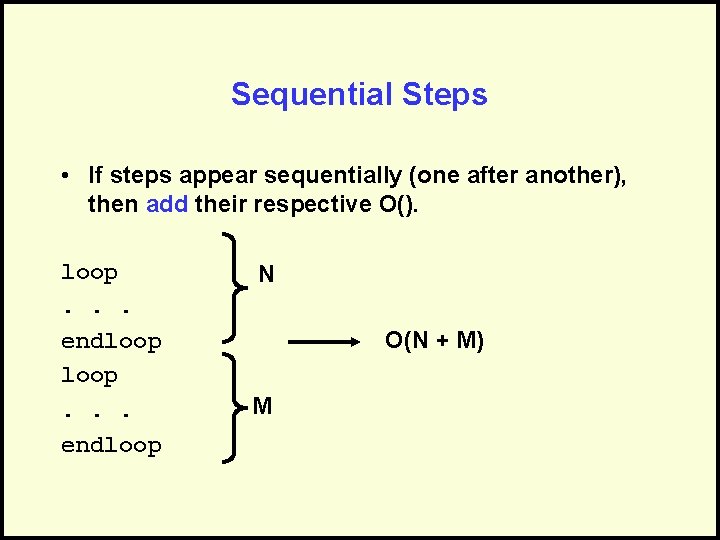
Sequential Steps • If steps appear sequentially (one after another), then add their respective O(). loop. . . endloop N O(N + M) M
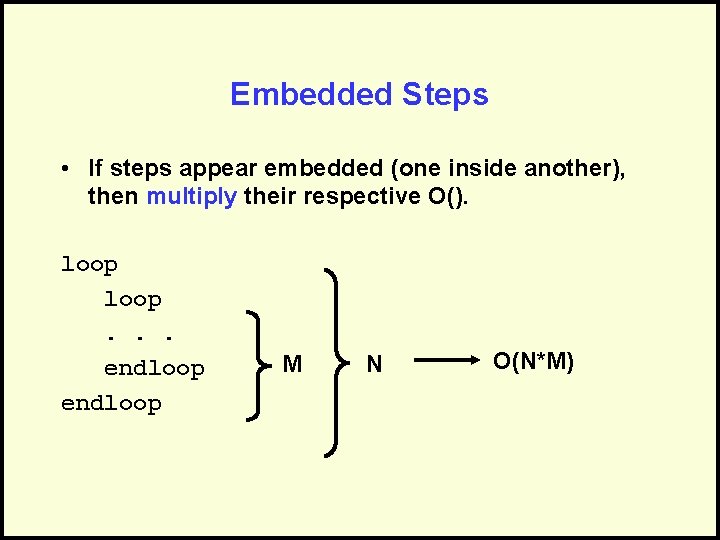
Embedded Steps • If steps appear embedded (one inside another), then multiply their respective O(). loop. . . endloop M N O(N*M)

Correctly Determining O() • Can have multiple factors: – O(N*M) – O(log. P + N 2) • But keep only the dominant factors: – O(N + Nlog. N) O(Nlog. N) – O(N*M + P) remains the same – O(V 2 + Vlog. V) • Drop constants: – O(2 N + 3 N 2) O(V 2) O(N + N 2) O(N 2)

Summary • We use O() notation to discuss the rate at which the work of an algorithm grows with respect to the size of the input. • O() is an upper bound, so only keep dominant terms and drop constants

Questions?

- Slides: 42