New features dispersions function of the current material

























- Slides: 70



New features







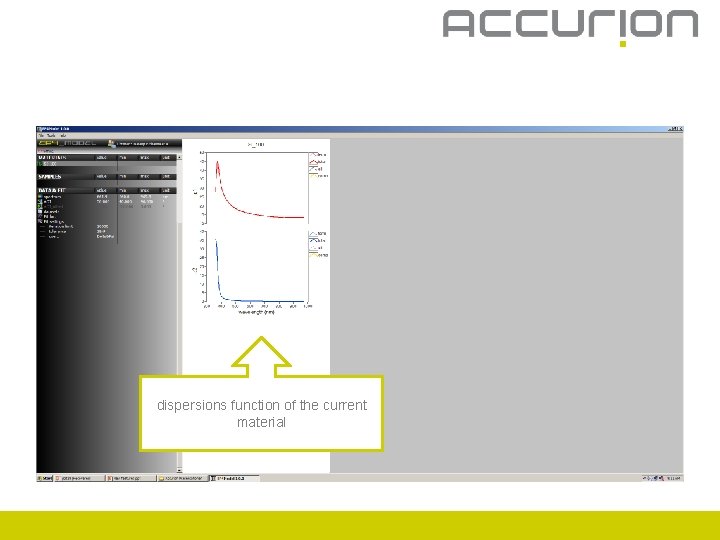
dispersions function of the current material




















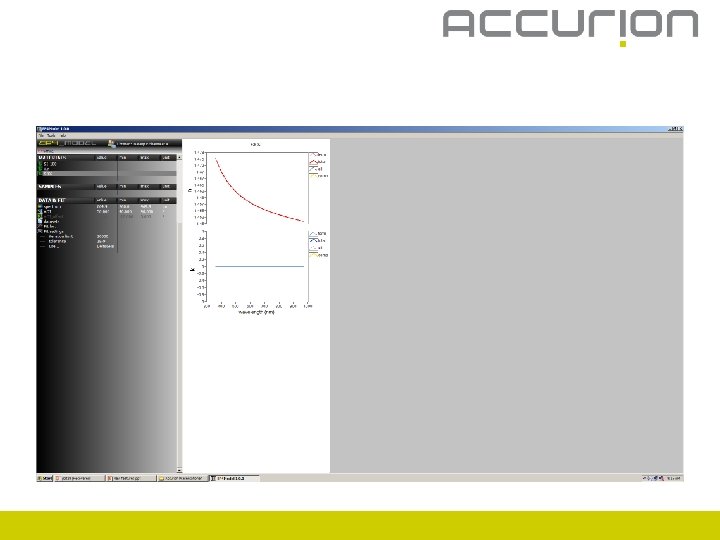
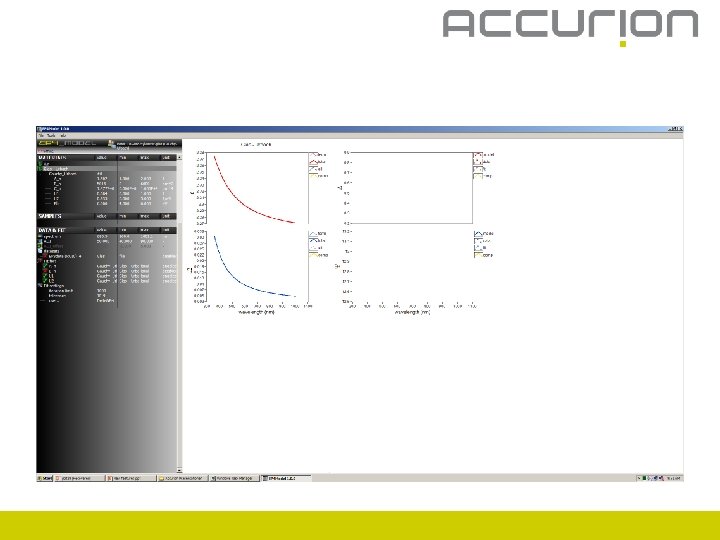
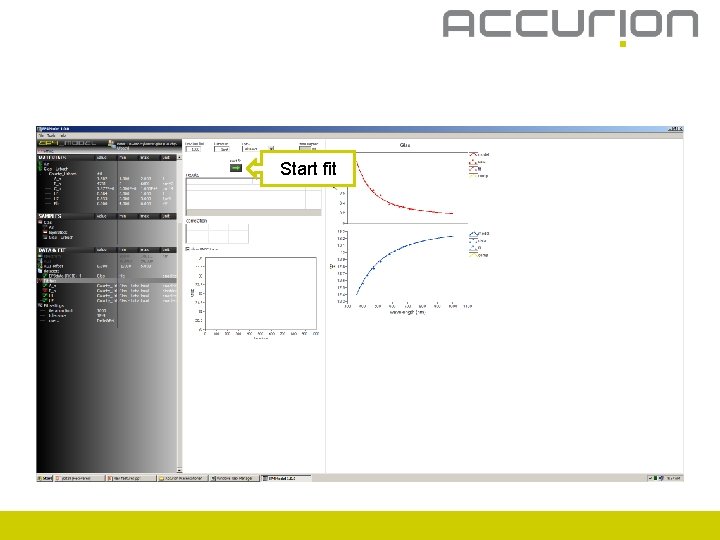
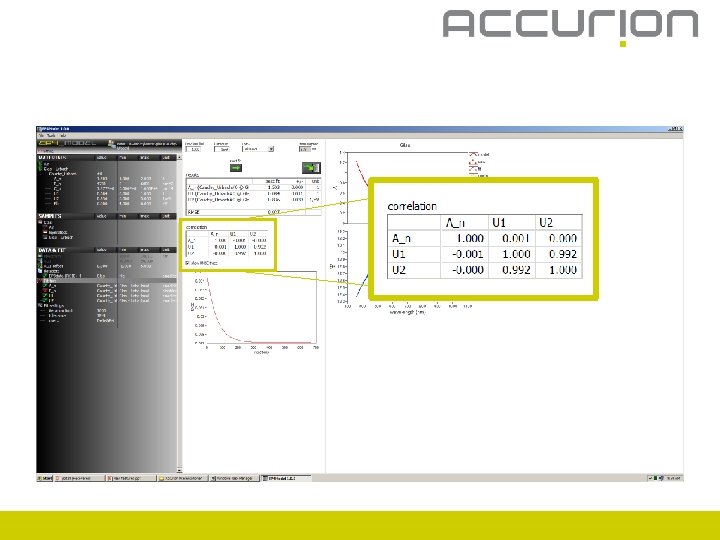
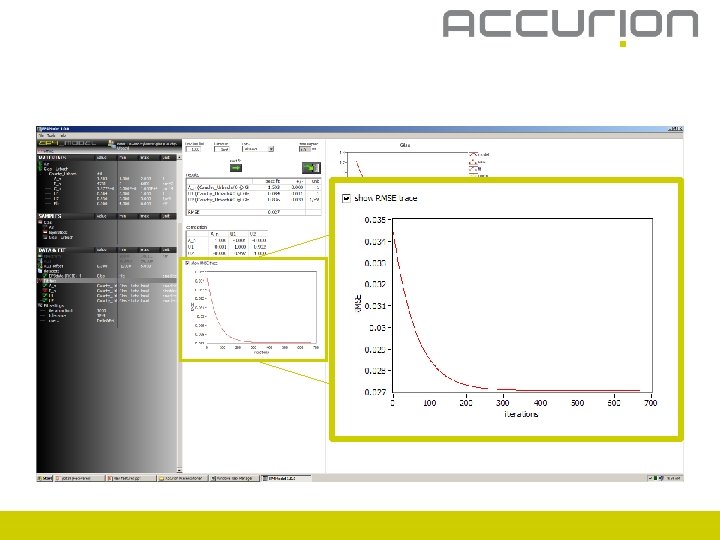
Start fit





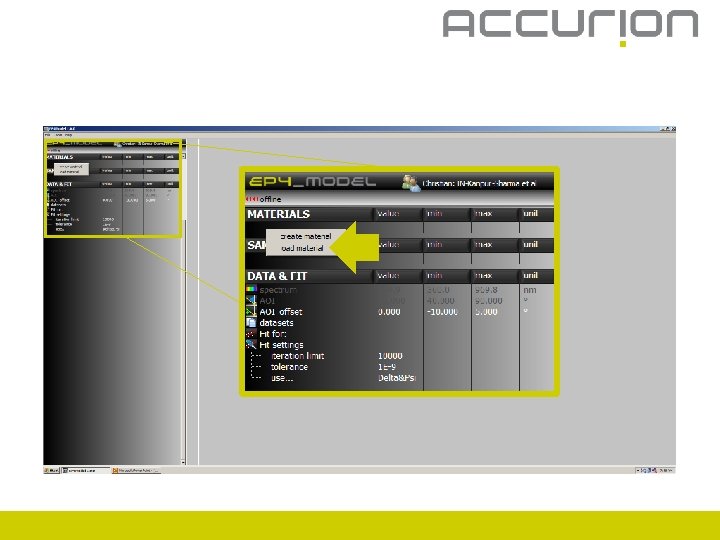
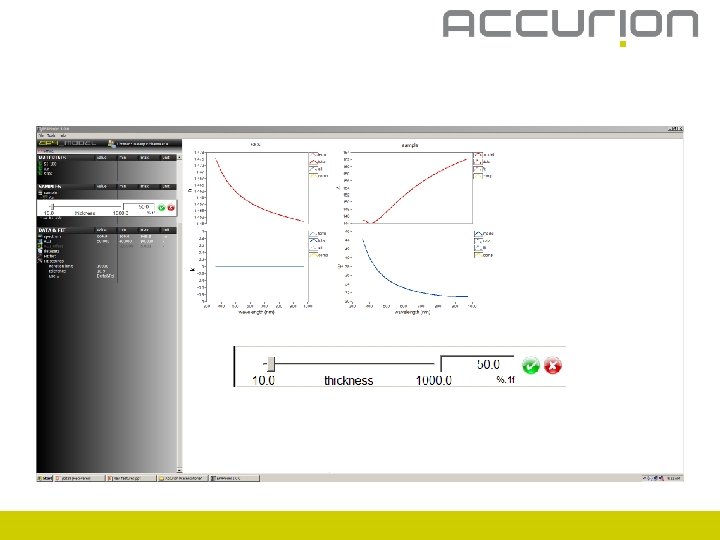
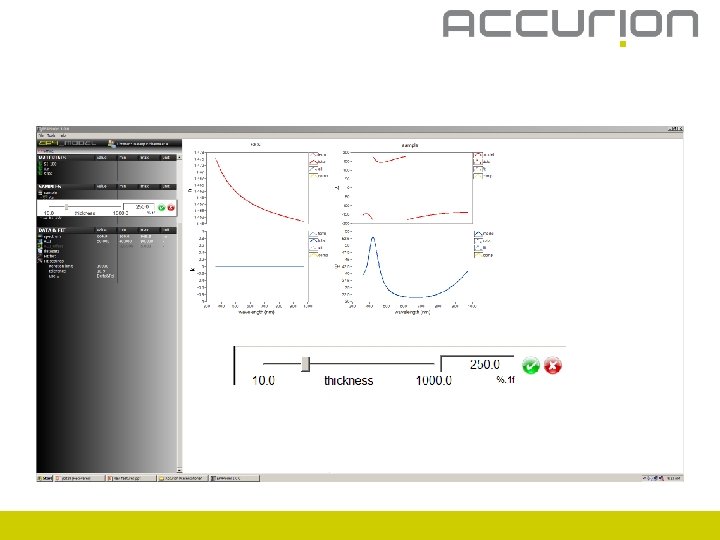
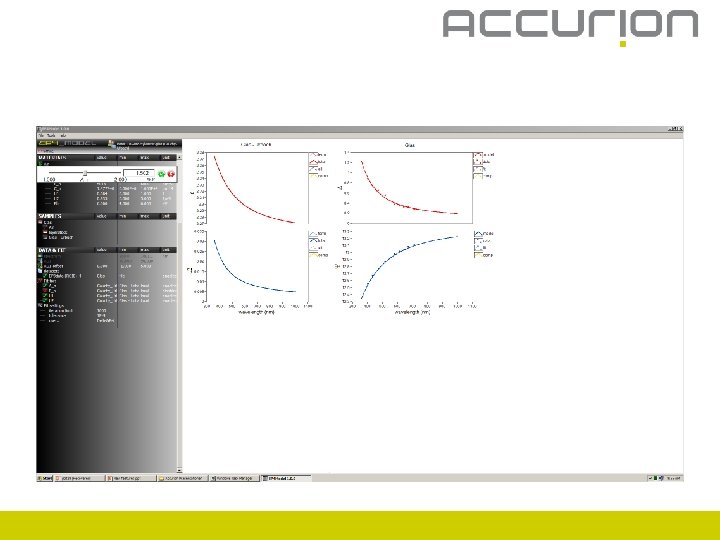
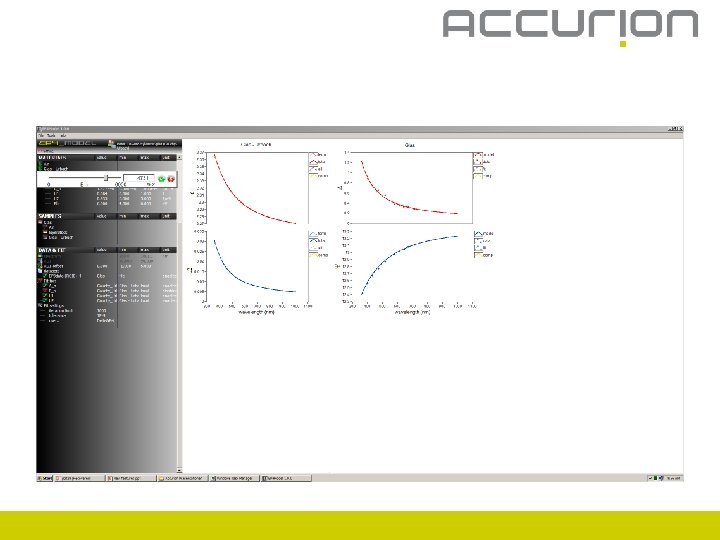
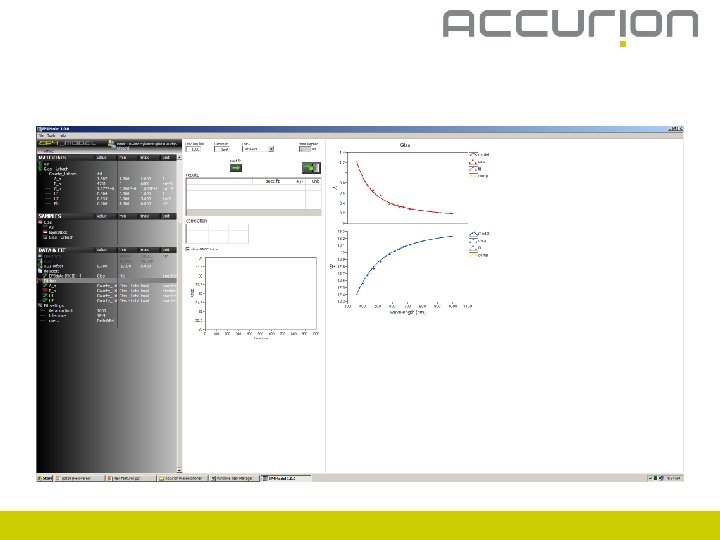
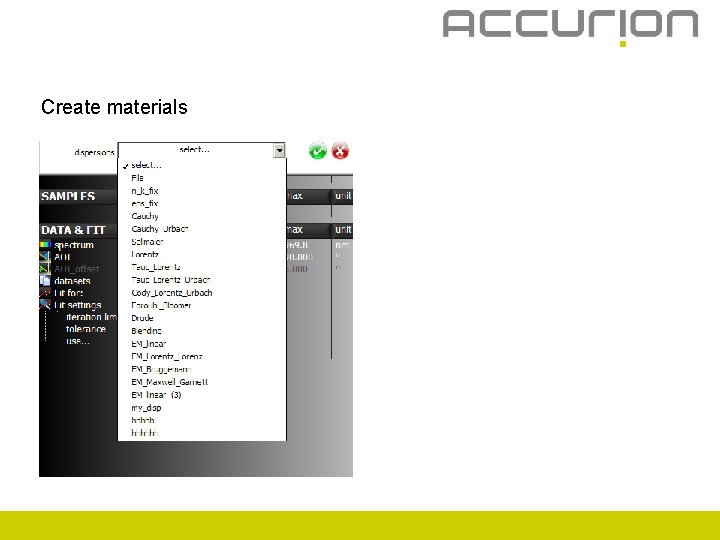
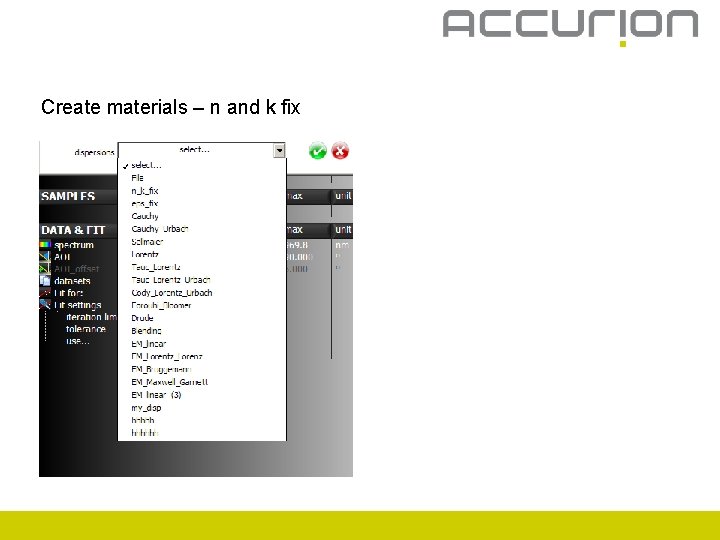
Create materials

Create materials – n and k fix

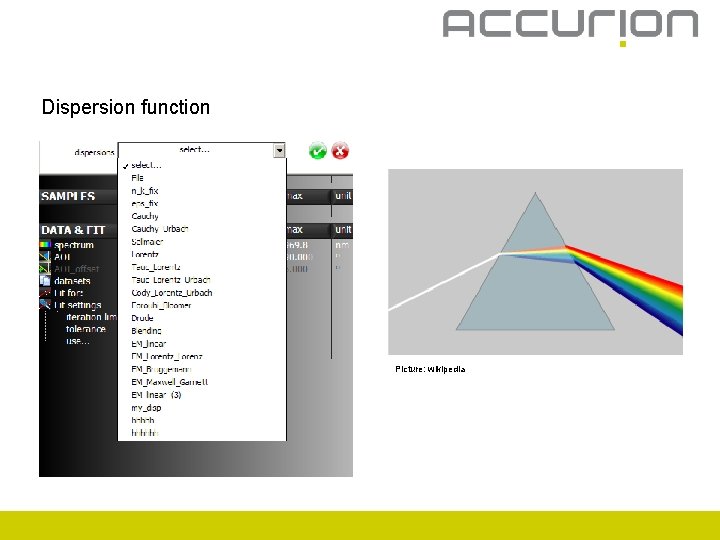
Dispersion function Picture: wikipedia

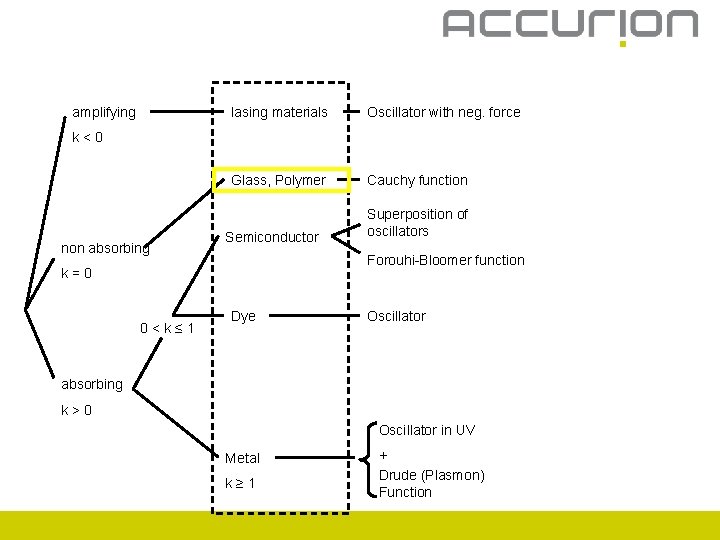
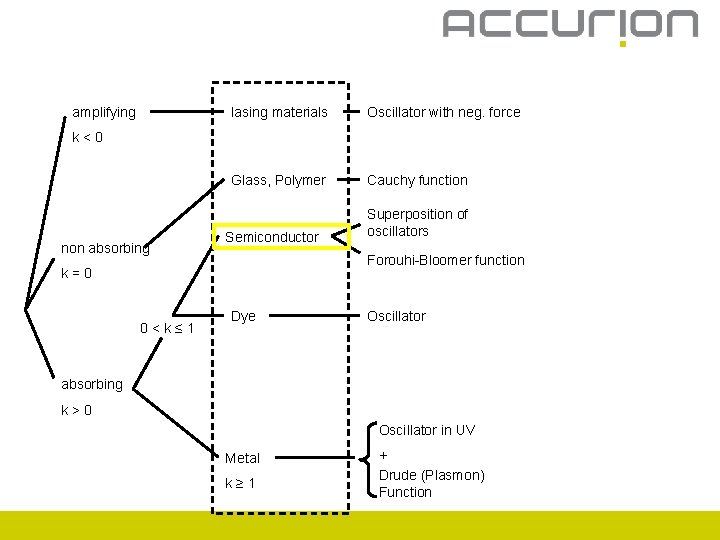
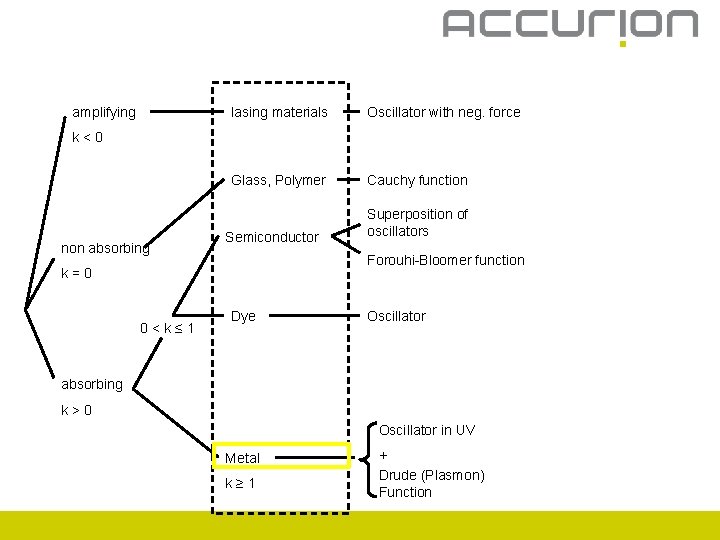
amplifying lasing materials Oscillator with neg. force Glass, Polymer Cauchy function k<0 non absorbing Semiconductor Forouhi-Bloomer function k=0 0<k≤ 1 Superposition of oscillators Dye Oscillator absorbing k>0 Oscillator in UV Metal k≥ 1 + Drude (Plasmon) Function

Cauchy: in general Picture: wikipedia

Cauchy: for n and k Picture: wikipedia

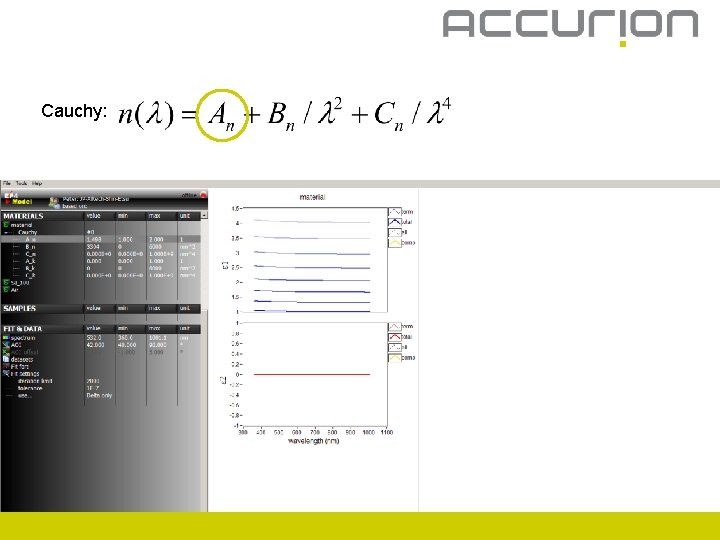
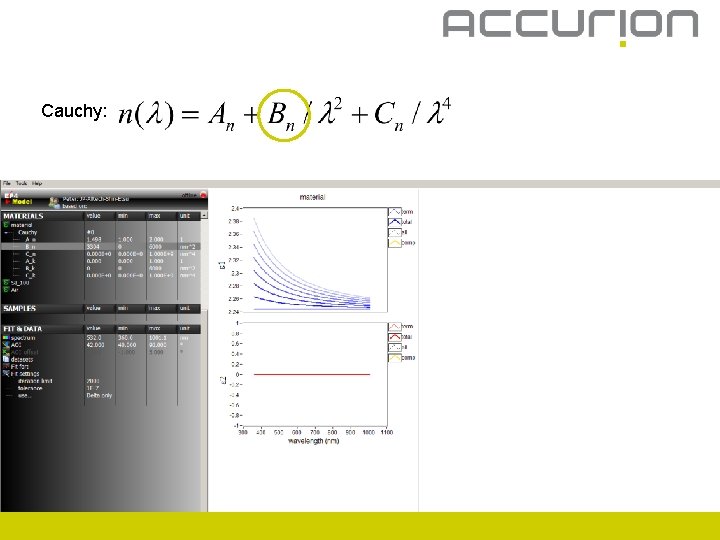
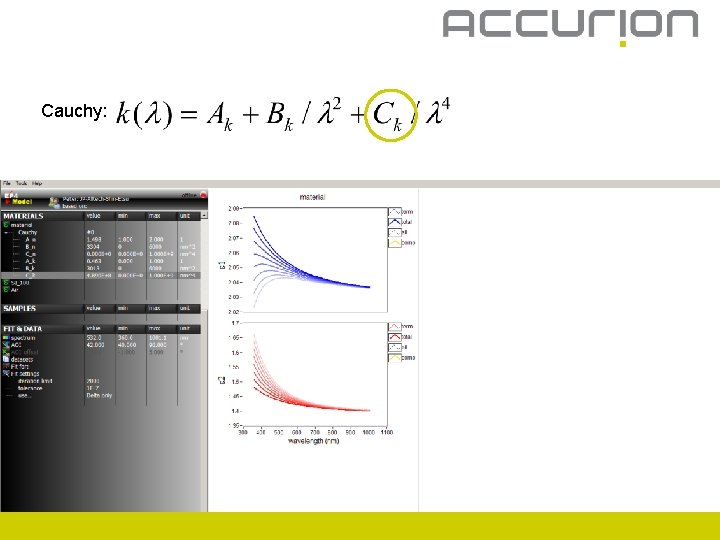
Cauchy:

Cauchy:

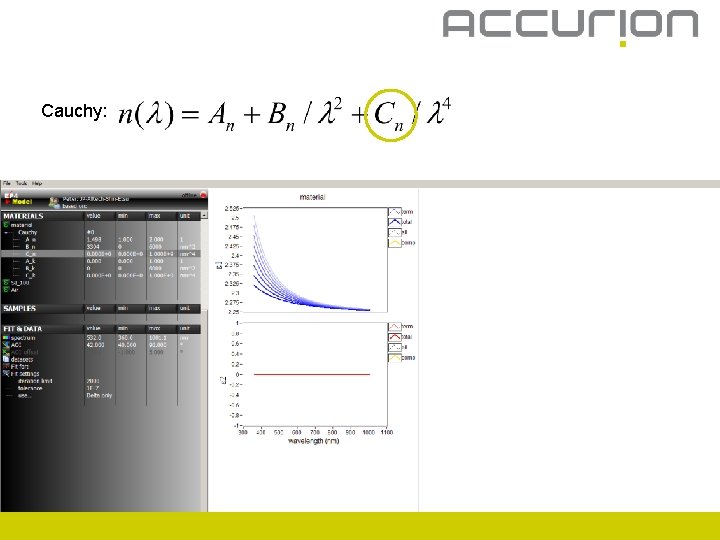
Cauchy:

Cauchy:

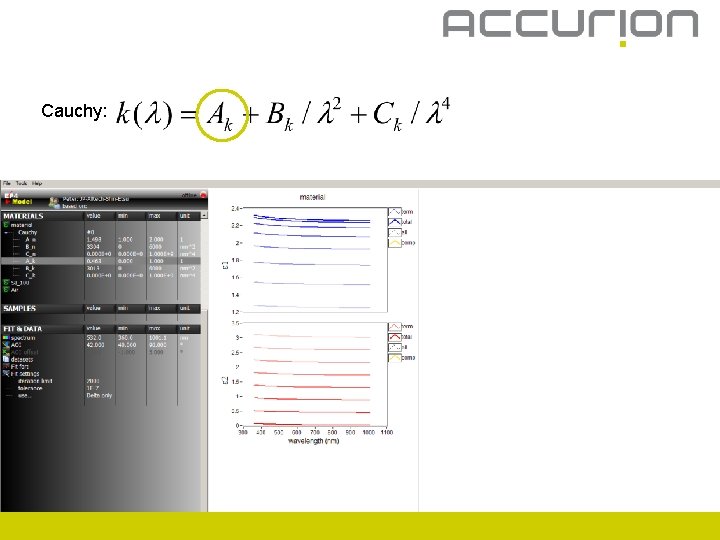
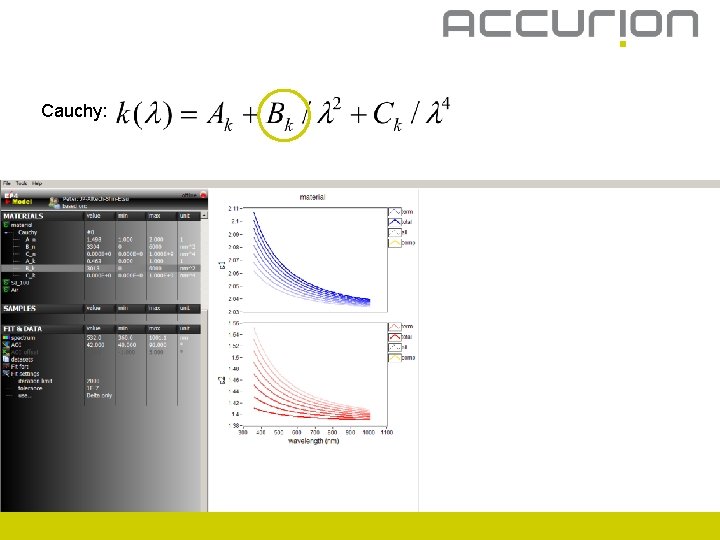
Cauchy:

Cauchy:

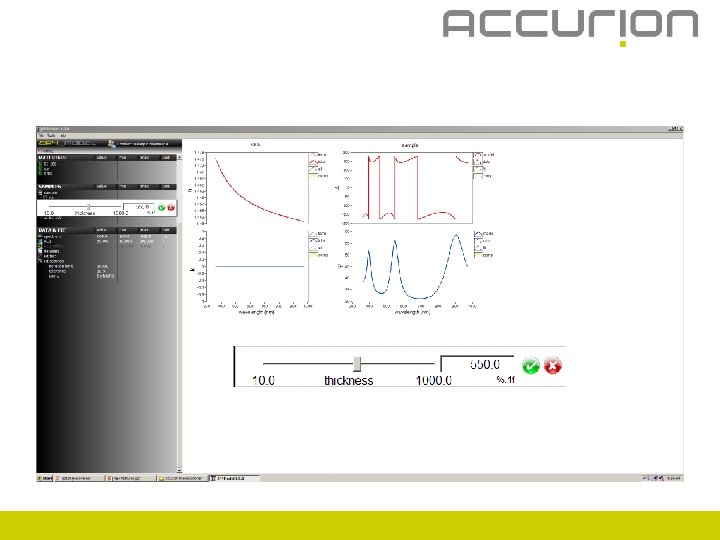
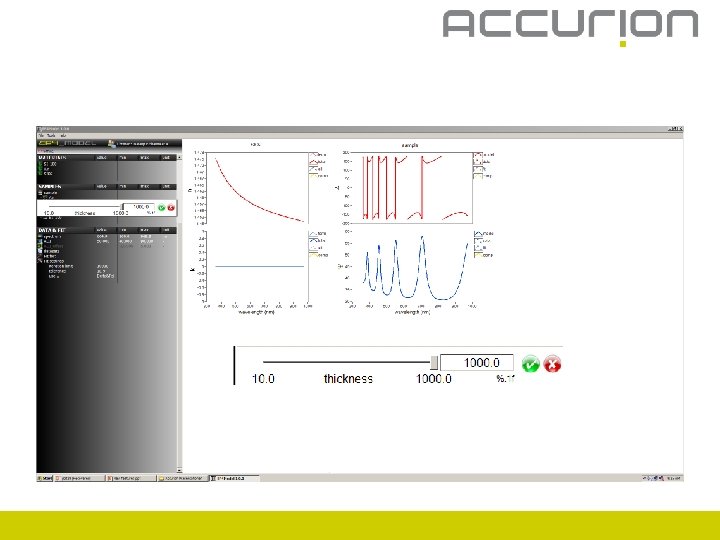
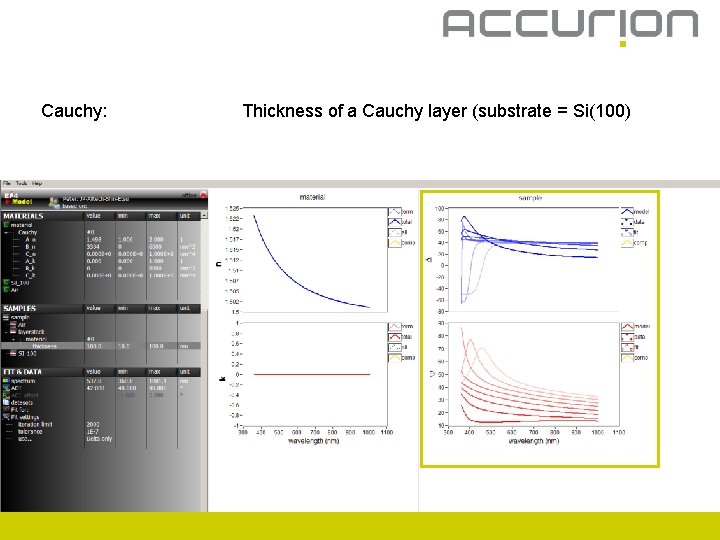
Cauchy: Thickness of a Cauchy layer (substrate = Si(100)

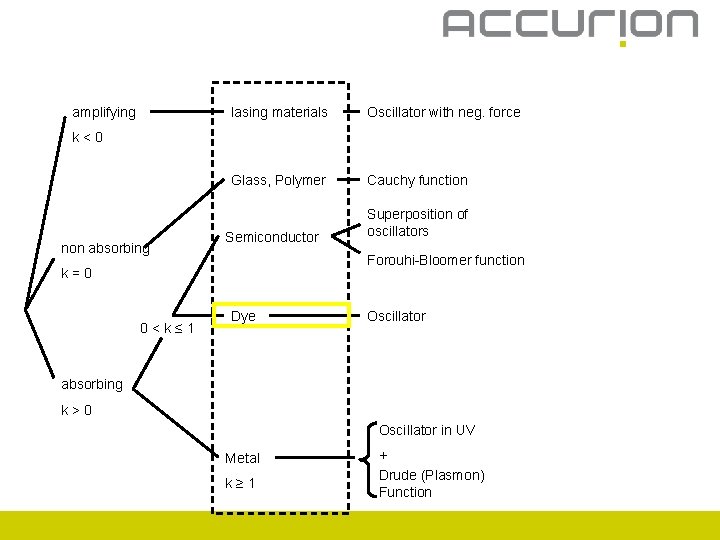
amplifying lasing materials Oscillator with neg. force Glass, Polymer Cauchy function k<0 non absorbing Semiconductor Forouhi-Bloomer function k=0 0<k≤ 1 Superposition of oscillators Dye Oscillator absorbing k>0 Oscillator in UV Metal k≥ 1 + Drude (Plasmon) Function

amplifying lasing materials Oscillator with neg. force Glass, Polymer Cauchy function k<0 non absorbing Semiconductor Forouhi-Bloomer function k=0 0<k≤ 1 Superposition of oscillators Dye Oscillator absorbing k>0 Oscillator in UV Metal k≥ 1 + Drude (Plasmon) Function

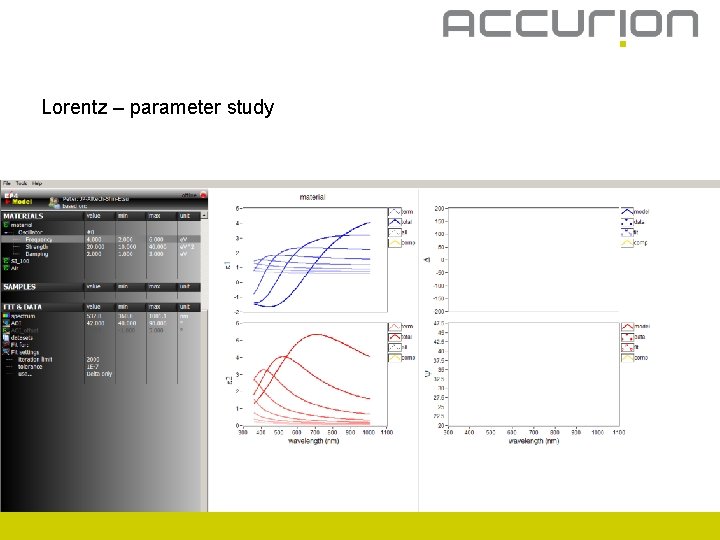
Lorentz – parameter study

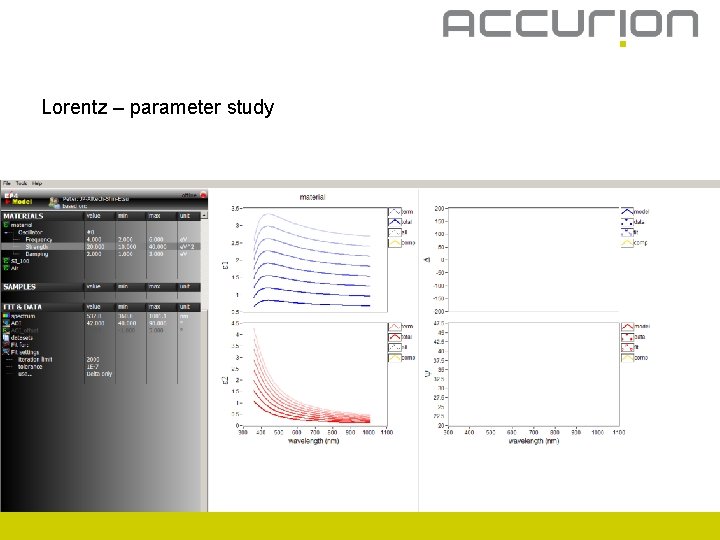
Lorentz – parameter study

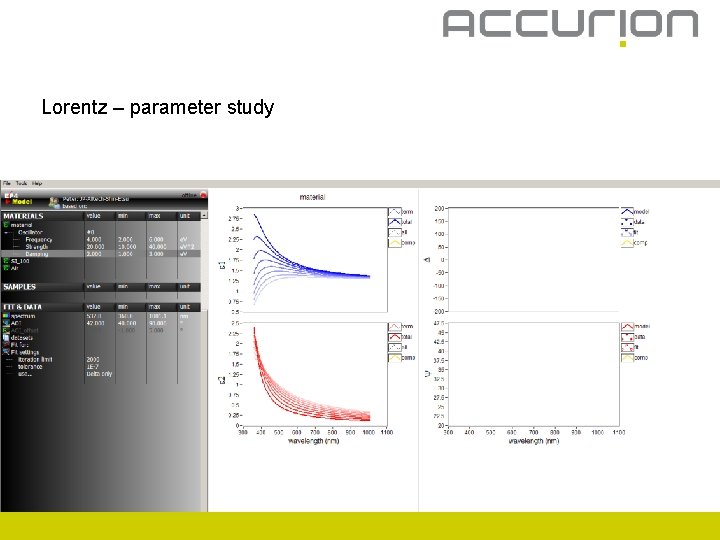
Lorentz – parameter study

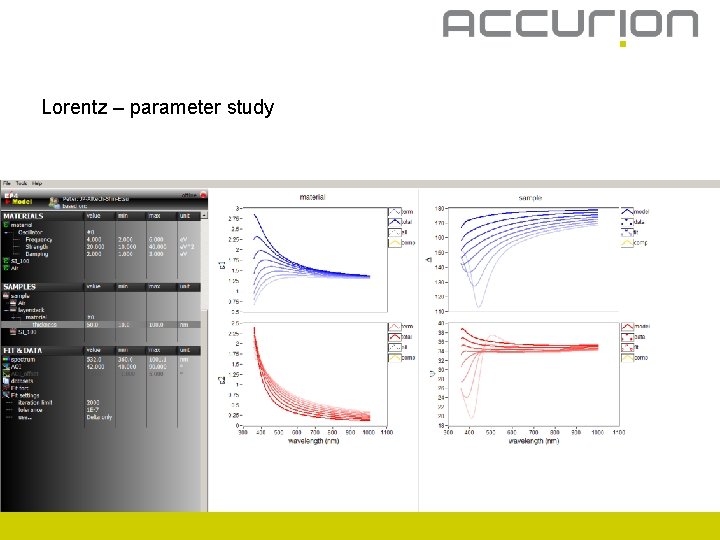
Lorentz – parameter study

amplifying lasing materials Oscillator with neg. force Glass, Polymer Cauchy function k<0 non absorbing Semiconductor Forouhi-Bloomer function k=0 0<k≤ 1 Superposition of oscillators Dye Oscillator absorbing k>0 Oscillator in UV Metal k≥ 1 + Drude (Plasmon) Function

Drude Picture: wikipedia

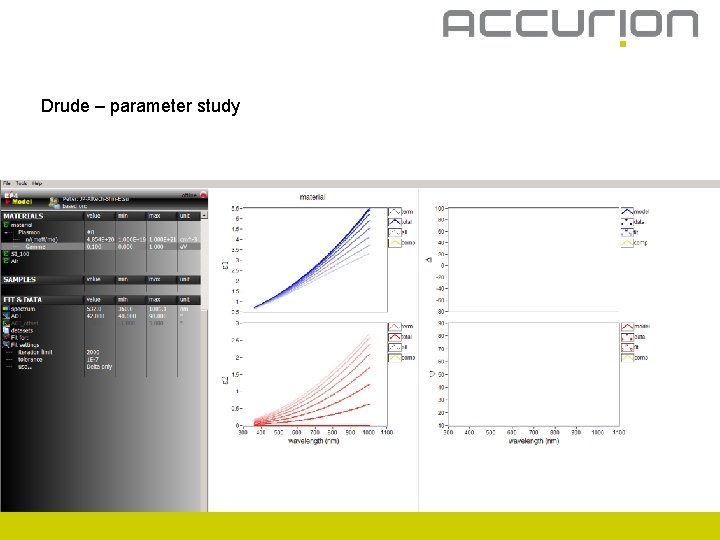
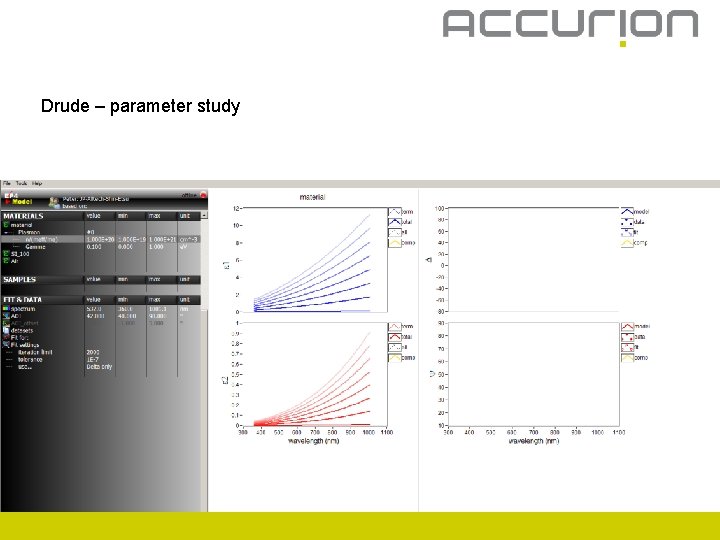
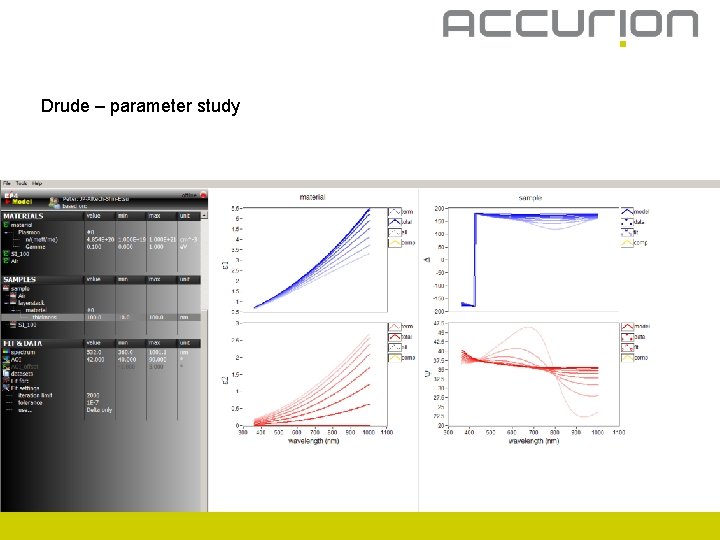
Drude – parameter study

Drude – parameter study

Drude – parameter study

Dispersion functions: Effective medium approach Layers out of two components

Dispersion functions: Effective medium approach Incomplete layers – material + void

Dispersion functions: Effective medium approach Surface roughtness

Lorentz-Lorentz: eh = 1 The host is chosen as air. This is the earliest EMA theory, and is based on the Clausius. Mossotti equation. It assumes that the individual constituents are mixed on the atomic scale, and is therefore of limited usefulness in describing real materials, which tend to be mixed on a much larger scale. Tompkins HG, Irene EA (2005) Handbook of Ellipsometry. William Andrew Publishing. NY

Maxwell-Garnett: eh = e 1 The host material is the material that has the largest constituent fraction. This is the most realistic EMA theory when the fraction of inclusions is significantly less than the fraction of host material. This EMA is very useful for cermats or for certain types of nanocrystals embedded in hosts well below the perculation threshold. Tompkins HG, Irene EA (2005) Handbook of Ellipsometry. William Andrew Publishing. NY

Bruggeman: eh = < e > the host material is just the EMA dielectric function. The Bruggeman EMA makes no assumption concerning the material that has the highest constituent fraction, and is therefore self-consistent. It is most useful when no constituent forms a clear majority of the material. Tompkins HG, Irene EA (2005) Handbook of Ellipsometry. William Andrew Publishing. NY

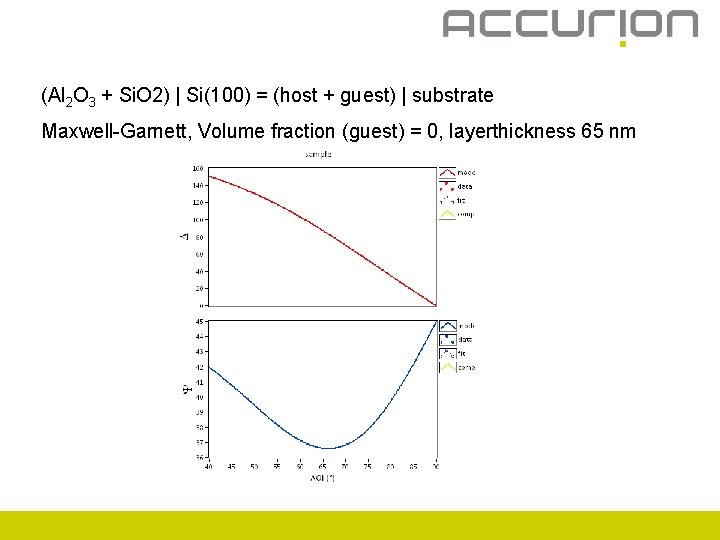
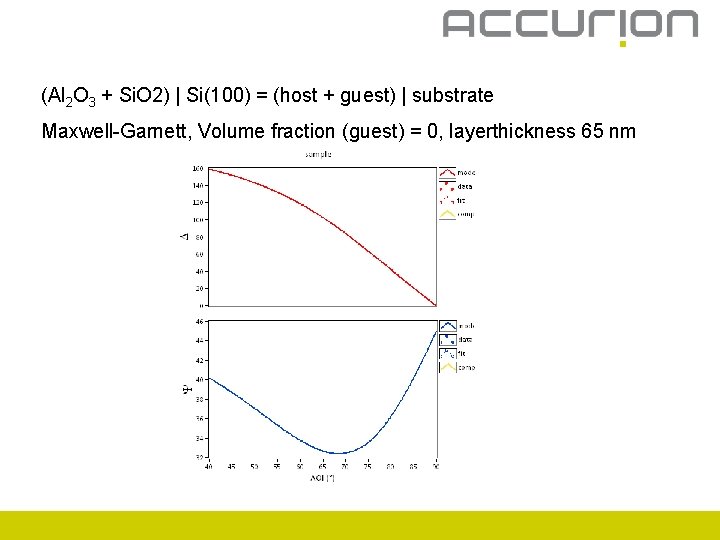
(Al 2 O 3 + Si. O 2) | Si(100) = (host + guest) | substrate Maxwell-Garnett, Volume fraction (guest) = 0, layerthickness 65 nm

(Al 2 O 3 + Si. O 2) | Si(100) = (host + guest) | substrate Maxwell-Garnett, Volume fraction (guest) = 0, layerthickness 65 nm

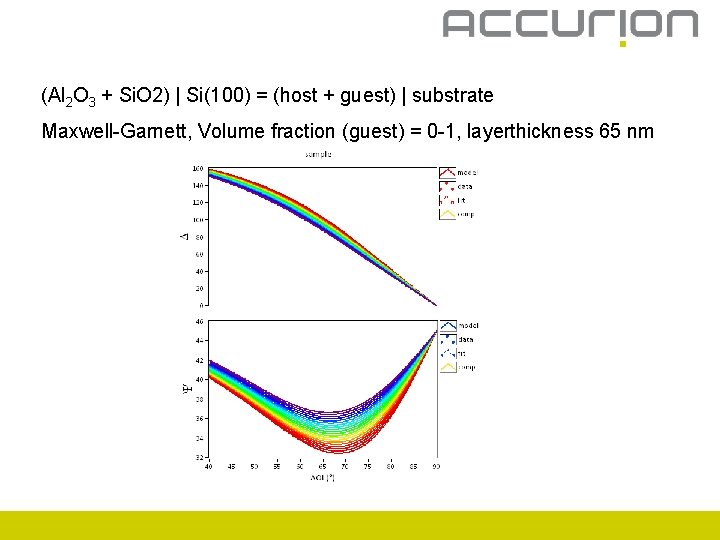
(Al 2 O 3 + Si. O 2) | Si(100) = (host + guest) | substrate Maxwell-Garnett, Volume fraction (guest) = 0 -1, layerthickness 65 nm

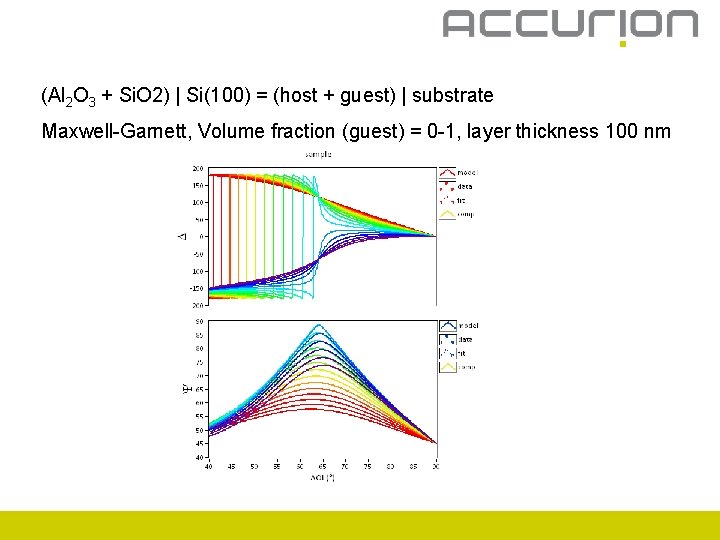
(Al 2 O 3 + Si. O 2) | Si(100) = (host + guest) | substrate Maxwell-Garnett, Volume fraction (guest) = 0 -1, layer thickness 100 nm

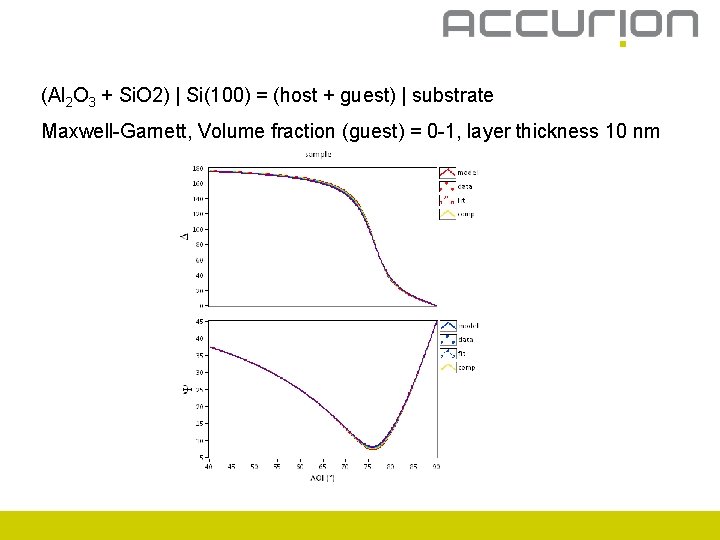
(Al 2 O 3 + Si. O 2) | Si(100) = (host + guest) | substrate Maxwell-Garnett, Volume fraction (guest) = 0 -1, layer thickness 10 nm

• Take home massage: – Interactive and easy to use new thin film modeling software – inspiring confidence by “see what you are doing as you do it” – Better under