THREE PHASE SYSTEMS Part 1 1 Objectives q

THREE PHASE SYSTEMS Part 1 1

Objectives q Become familiar with the operation of a three phase generator and the magnitude and phase relationship. q Be able to calculate the voltages and currents for a three phase Wye and Delta connected generator and load. 2

Introduction Rotor Stator Rotor q An ac generator designed to develop a single sinusoidal voltage for each rotation of the shaft (rotor) is referred to as a single-phase ac generator 3

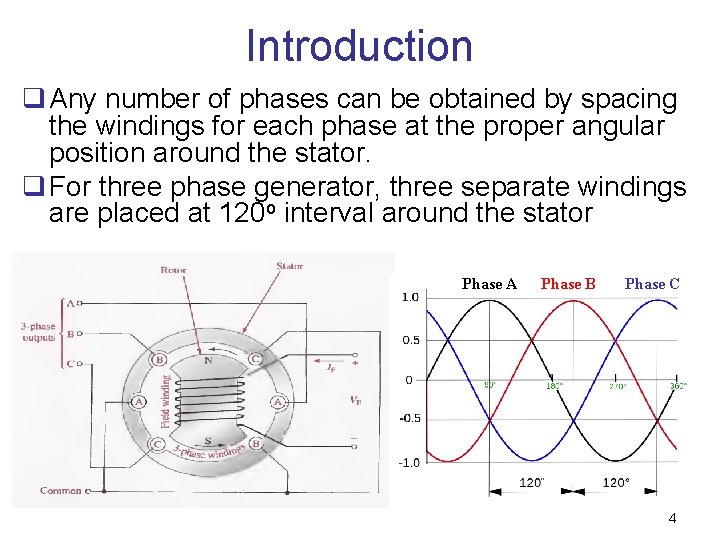
Introduction q Any number of phases can be obtained by spacing the windings for each phase at the proper angular position around the stator. q For three phase generator, three separate windings are placed at 120 o interval around the stator Phase A Phase B Phase C 4

Introduction Why use three phase system? ? 1. Requires lesser amount of material (copper) for transferring the same amount of power 2. The lighter lines are easier to install, and the supporting structures can be less massive and farther apart 3. A three-phase machine gives more output compared to a single-phase machine of the same size. 4. Domestic power and industrial or commercial power can be supplied from the same source. 5. Three-phase induction motors are self-starting, whereas single-phase motors are not self-starting. 5

Introduction q Generated frequency depends on q. Number of poles on the rotor q. Speed of rotor q Frequency variation q 60 Hz (US, Canada etc) q 50 Hz (Europe, Malaysia etc) q 400 Hz (Aircraft and ship) q Amplitude variation q 220 V – 240 V q 100 V – 127 V 6

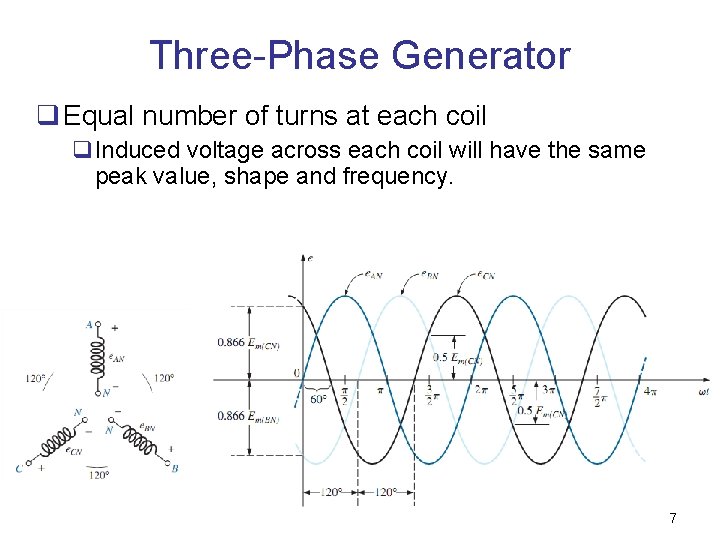
Three-Phase Generator q Equal number of turns at each coil q. Induced voltage across each coil will have the same peak value, shape and frequency. 7

Three-Phase Generator q At any instance, algebraic sum of the three phase voltages of a three-phase generator is zero. 8

Three-Phase Generator q The sinusoidal expression for each of the induced voltage is: Phasor Form 9

Connection in Three Phase System • A 3 -phase system is equivalent to three single phase circuit • Two possible configurations in three phase system: 1. Y-connection (star connection) 2. ∆-connection (delta connection) 10

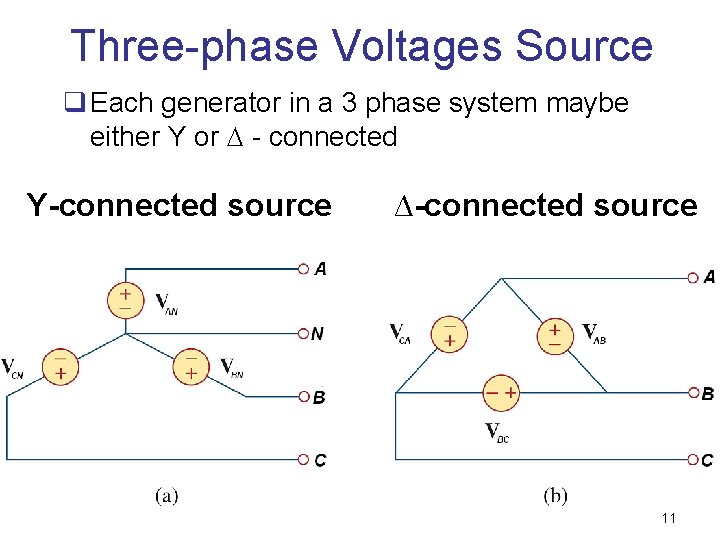
Three-phase Voltages Source q Each generator in a 3 phase system maybe either Y or - connected Y-connected source ∆-connected source 11

Three-phase Load q Loads may be mixed on a power system. Y-connected load ∆-connected Mixed load 12

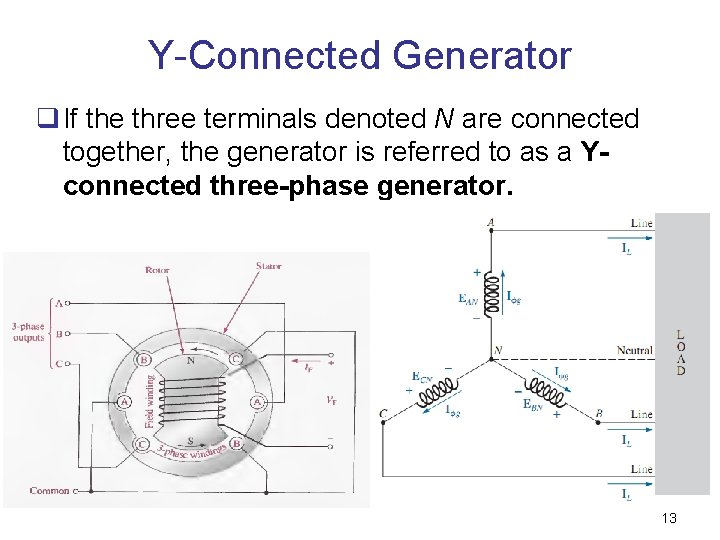
Y-Connected Generator q If the three terminals denoted N are connected together, the generator is referred to as a Yconnected three-phase generator. 13

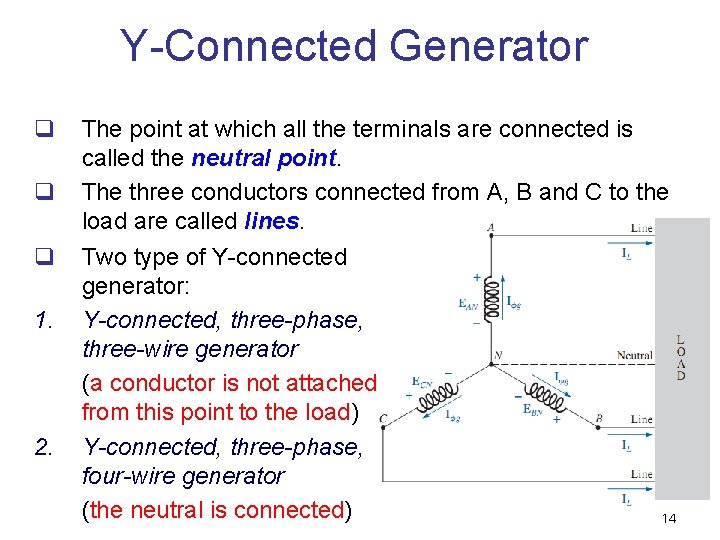
Y-Connected Generator q q q 1. 2. The point at which all the terminals are connected is called the neutral point. The three conductors connected from A, B and C to the load are called lines. Two type of Y-connected generator: Y-connected, three-phase, three-wire generator (a conductor is not attached from this point to the load) Y-connected, three-phase, four-wire generator (the neutral is connected) 14

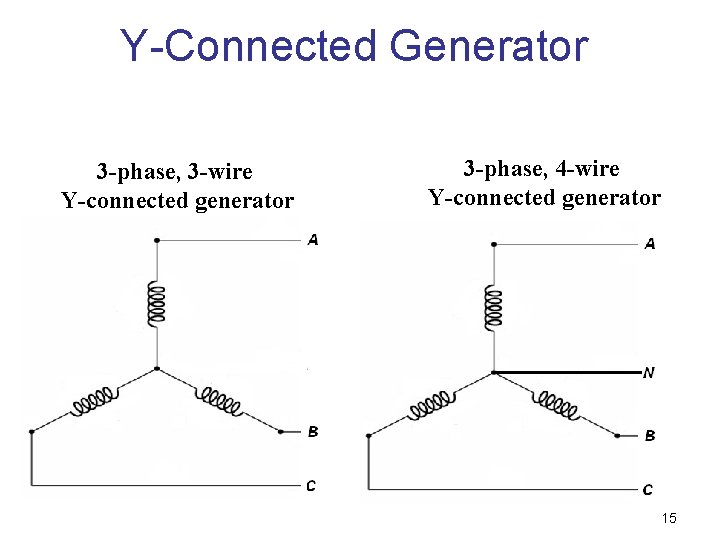
Y-Connected Generator 3 -phase, 3 -wire Y-connected generator 3 -phase, 4 -wire Y-connected generator 15

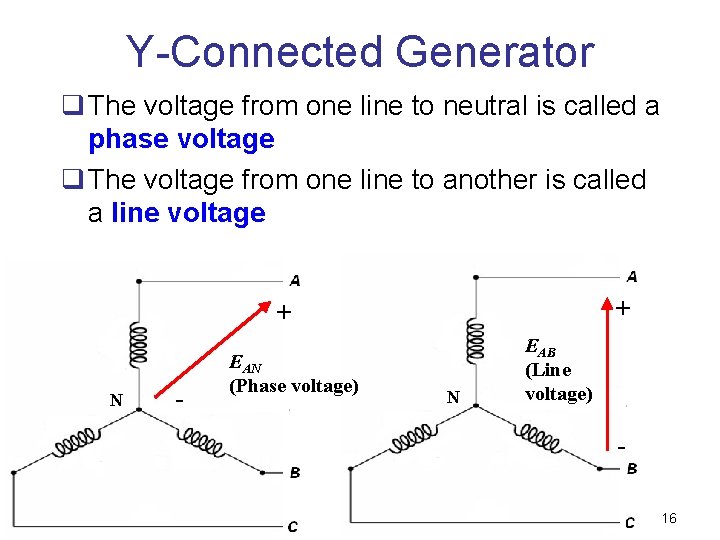
Y-Connected Generator q The voltage from one line to neutral is called a phase voltage q The voltage from one line to another is called a line voltage + + N - EAN (Phase voltage) N EAB (Line voltage) 16

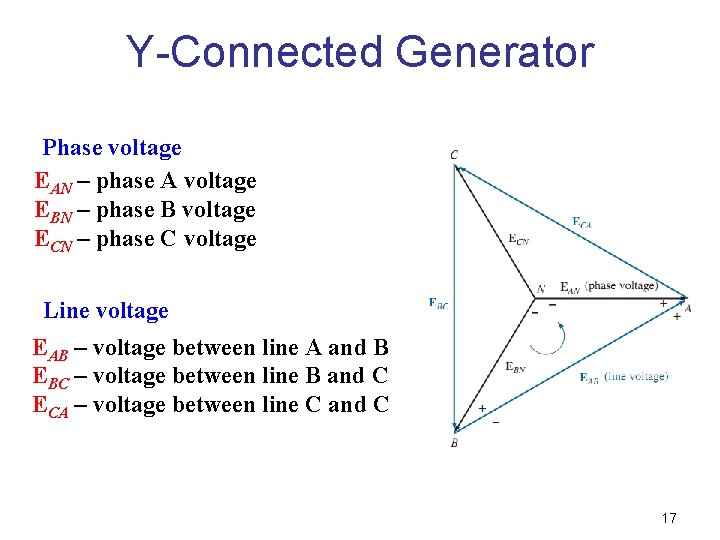
Y-Connected Generator Phase voltage EAN – phase A voltage EBN – phase B voltage ECN – phase C voltage Line voltage EAB – voltage between line A and B EBC – voltage between line B and C ECA – voltage between line C and C 17

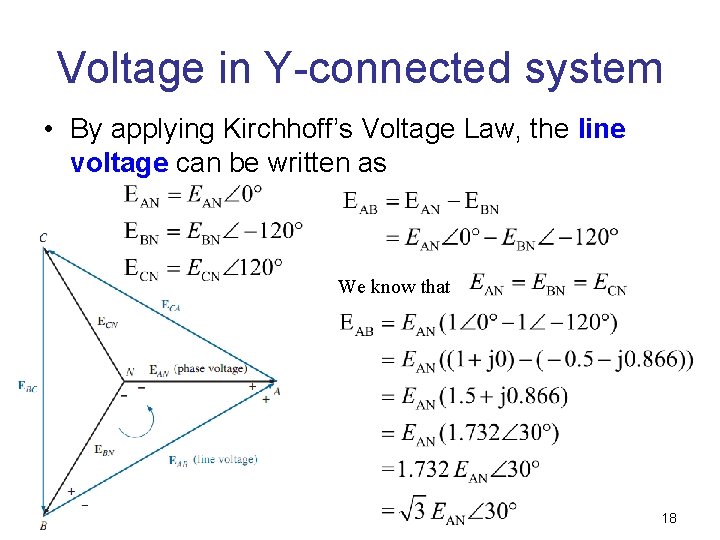
Voltage in Y-connected system • By applying Kirchhoff’s Voltage Law, the line voltage can be written as We know that 18

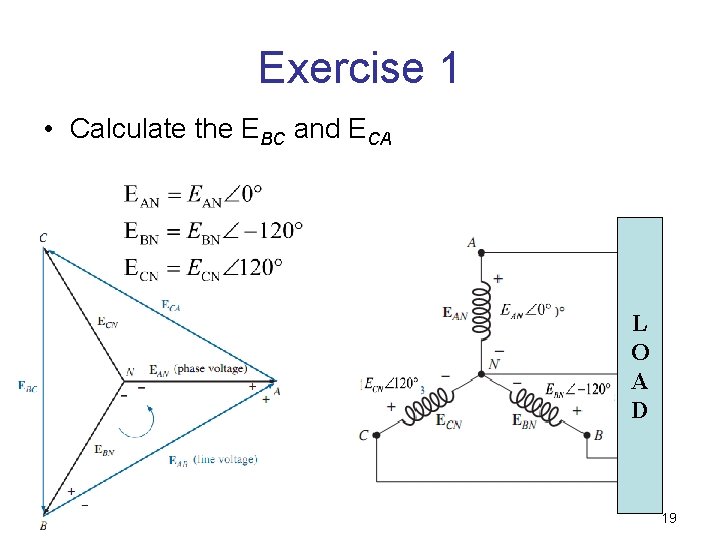
Exercise 1 • Calculate the EBC and ECA L O A D 19

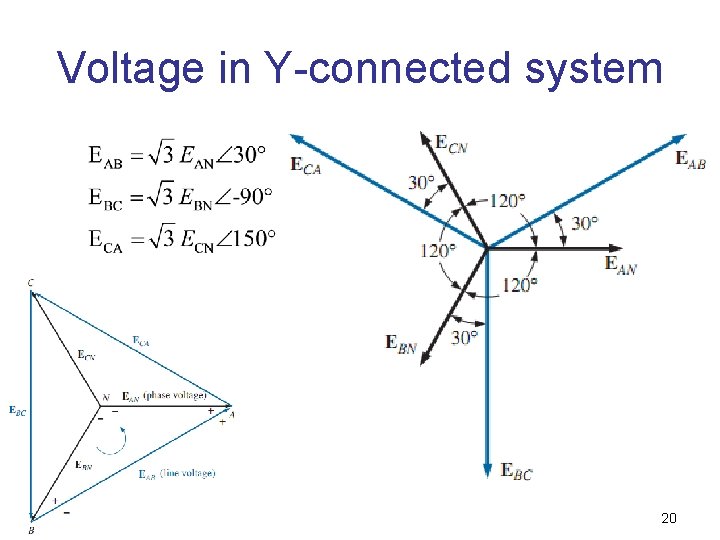
Voltage in Y-connected system 20

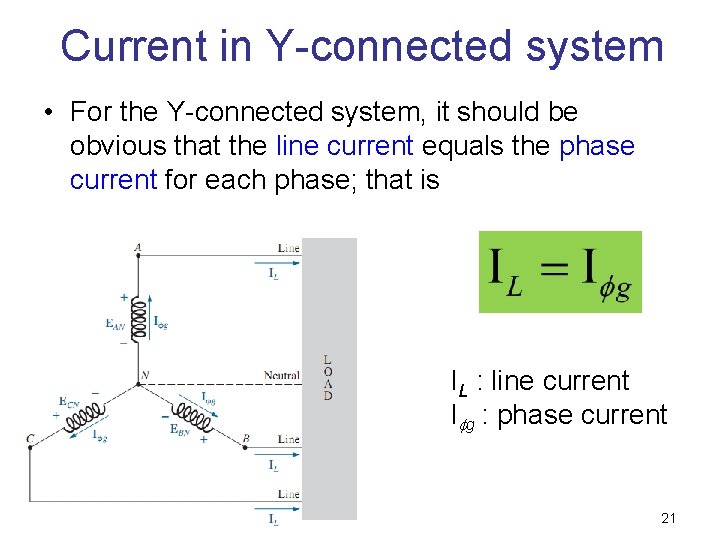
Current in Y-connected system • For the Y-connected system, it should be obvious that the line current equals the phase current for each phase; that is IL : line current I g : phase current 21

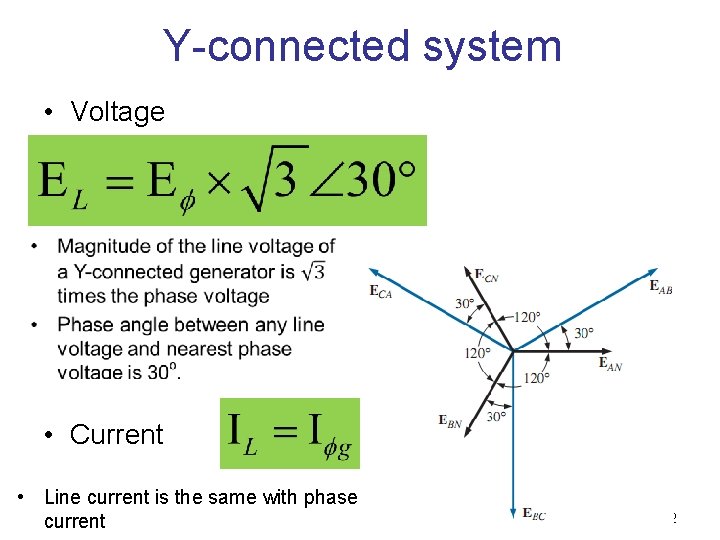
Y-connected system • Voltage • Current • Line current is the same with phase current 22

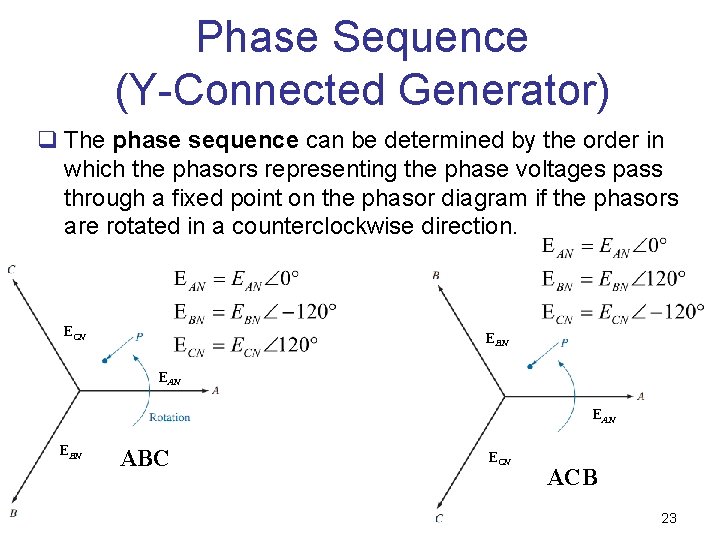
Phase Sequence (Y-Connected Generator) q The phase sequence can be determined by the order in which the phasors representing the phase voltages pass through a fixed point on the phasor diagram if the phasors are rotated in a counterclockwise direction. ECN EBN EAN EBN ABC ECN ACB 23

Phase Sequence (Y-Connected Generator) q. Significance of phase sequence. o Important in the three-phase distribution of power o In a three-phase motor, for example, if two phase voltages are interchanged, the sequence will change, and the direction of rotation of the motor will be reversed. 24

Exercise 2 Given o 1. For ABC phase sequence and 1 = 30 find 2 and 3. 2. For ACB phase sequence and 2 = -50 o find 1 and 3. o 3. For BCA phase sequence and 3 = 40 find 1 and 2. 25

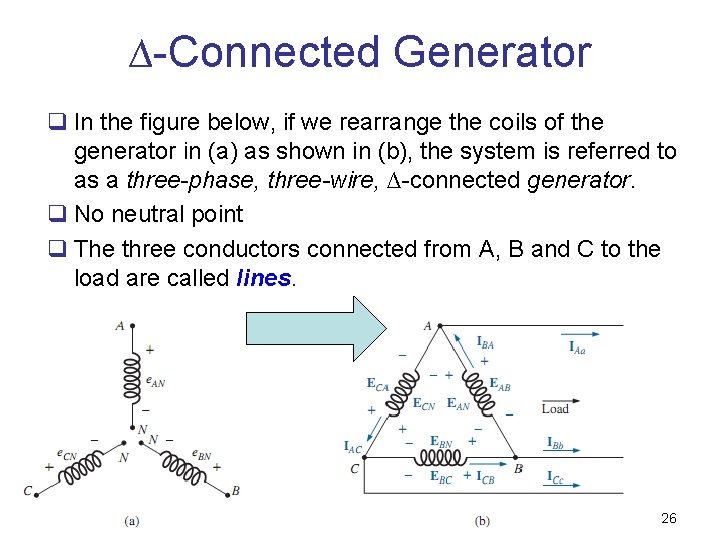
∆-Connected Generator q In the figure below, if we rearrange the coils of the generator in (a) as shown in (b), the system is referred to as a three-phase, three-wire, ∆-connected generator. q No neutral point q The three conductors connected from A, B and C to the load are called lines. 26

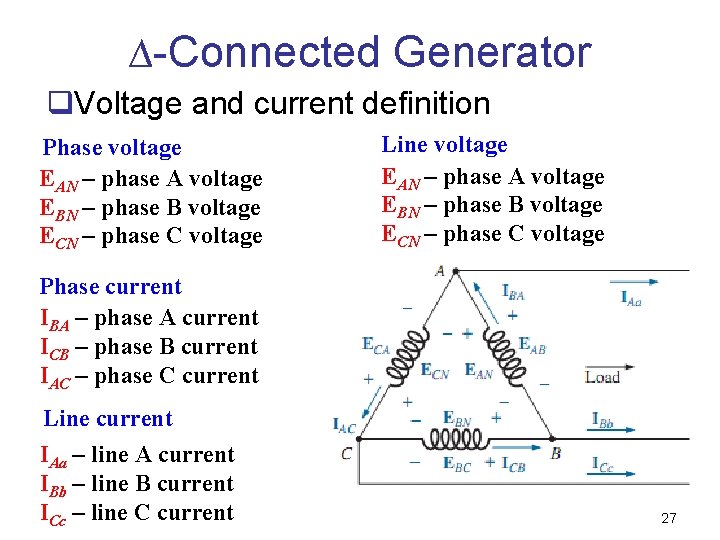
∆-Connected Generator q. Voltage and current definition Phase voltage EAN – phase A voltage EBN – phase B voltage ECN – phase C voltage Line voltage EAN – phase A voltage EBN – phase B voltage ECN – phase C voltage Phase current IBA – phase A current ICB – phase B current IAC – phase C current Line current IAa – line A current IBb – line B current ICc – line C current 27

Voltage in ∆-Connected System q. In this system, the phase and line voltages are equivalent and equal to the voltage induced across each coil of the generator: q. Only one voltage (magnitude) is available instead of the two in the Y-Connected system. 28

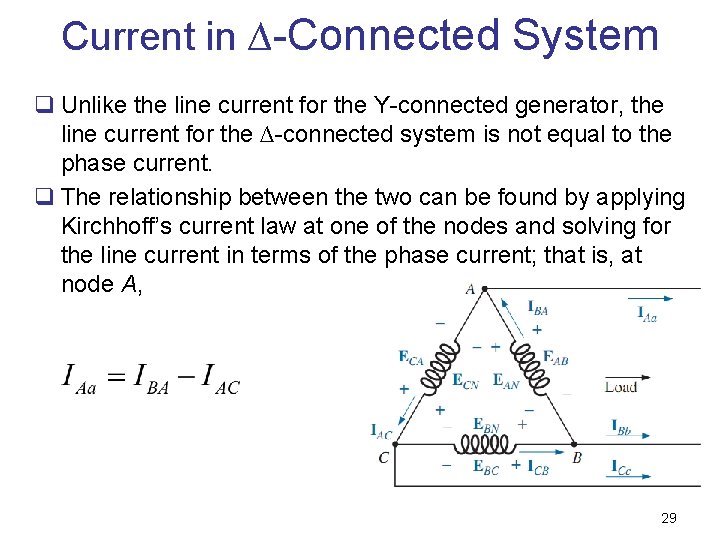
Current in ∆-Connected System q Unlike the line current for the Y-connected generator, the line current for the ∆-connected system is not equal to the phase current. q The relationship between the two can be found by applying Kirchhoff’s current law at one of the nodes and solving for the line current in terms of the phase current; that is, at node A, 29

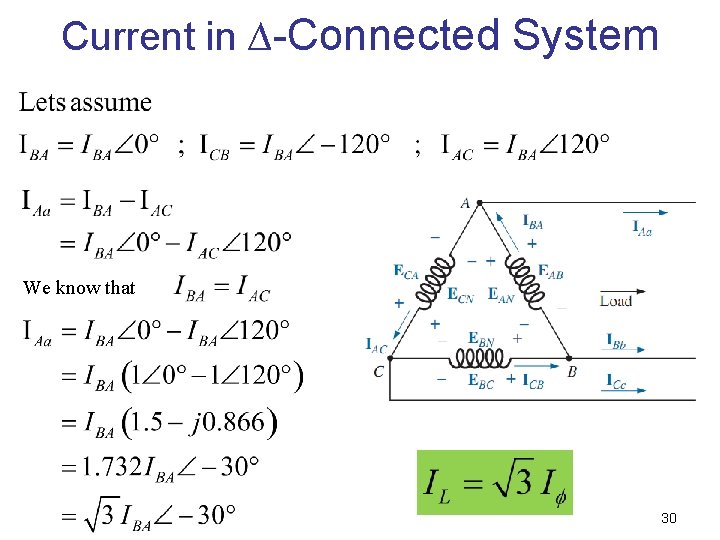
Current in ∆-Connected System We know that 30

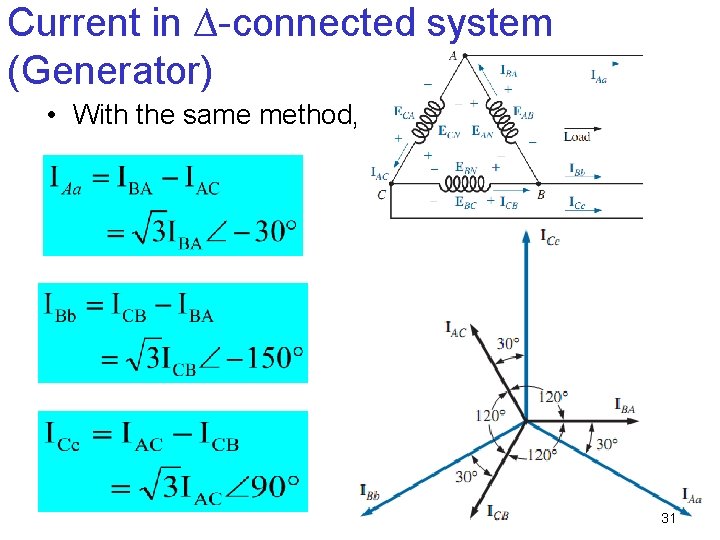
Current in ∆-connected system (Generator) • With the same method, 31

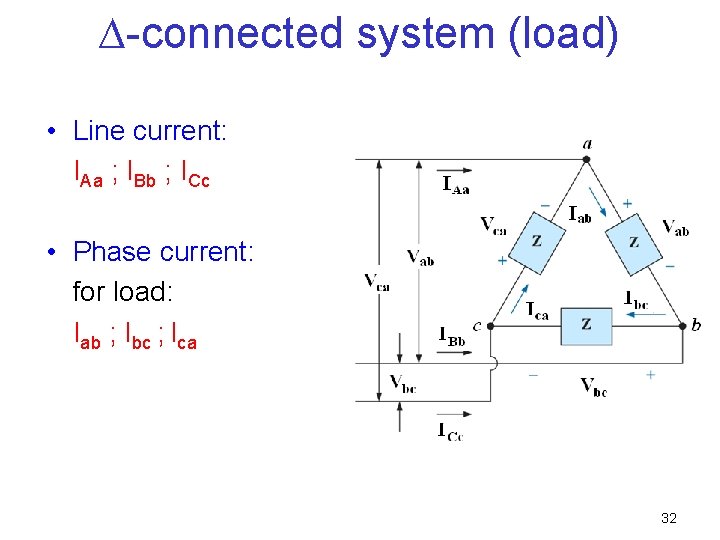
∆-connected system (load) • Line current: IAa ; IBb ; ICc • Phase current: for load: Iab ; Ibc ; Ica 32

∆ -connected system • Voltage • Line voltage is the same with phase voltage • Current 33

Phase Sequence (∆- Connected Generator) q Even though the line and phase voltages of a ∆ connected system are the same, it is standard practice to describe the phase sequence in terms of the line voltages q In drawing such a diagram, one must take care to have the sequence of the first and second subscripts the same q In phasor notation: 34

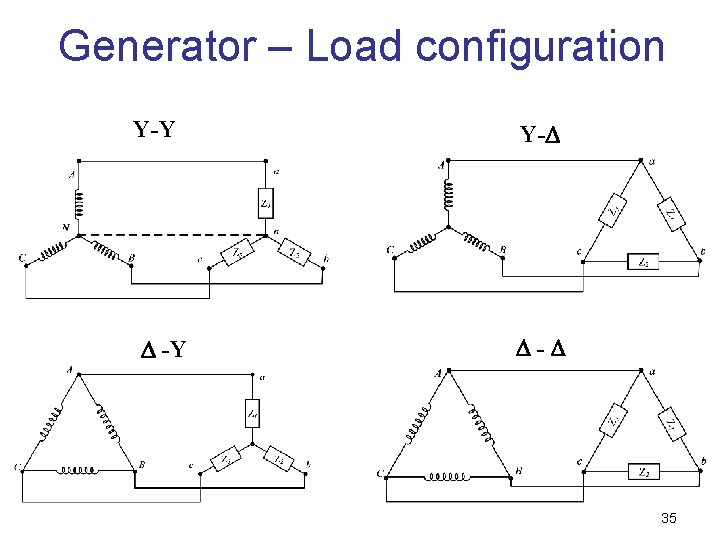
Generator – Load configuration Y-Y -Y Y- - 35

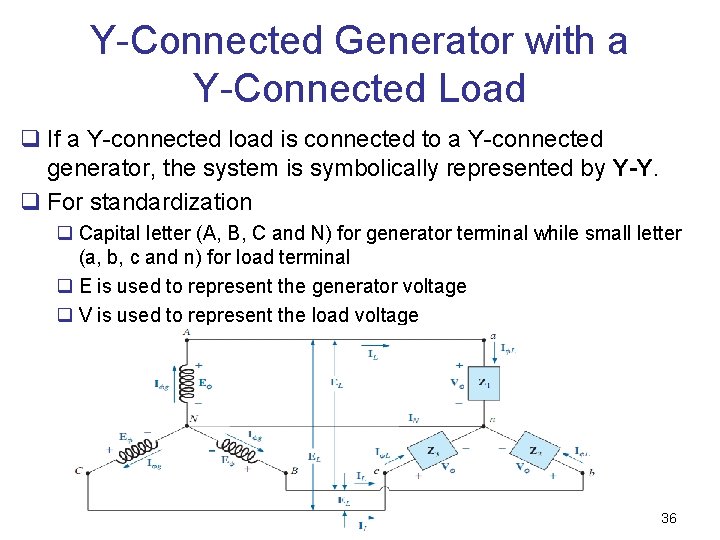
Y-Connected Generator with a Y-Connected Load q If a Y-connected load is connected to a Y-connected generator, the system is symbolically represented by Y-Y. q For standardization q Capital letter (A, B, C and N) for generator terminal while small letter (a, b, c and n) for load terminal q E is used to represent the generator voltage q V is used to represent the load voltage 36

Y-Connected Generator with a YConnected Load q For balanced load (Z 1 = Z 2 = Z 3) q neutral connection can be removed without affecting the circuit in any manner q Phase current (I ) will be the same in each phase q IN = 0. q For unbalanced load q neutral connection is required to conduct unbalanced current q Phase current (I ) will not be the same in each phase q In either case, the line voltage is q For both cases (balanced and unbalanced load) the line voltage is 37

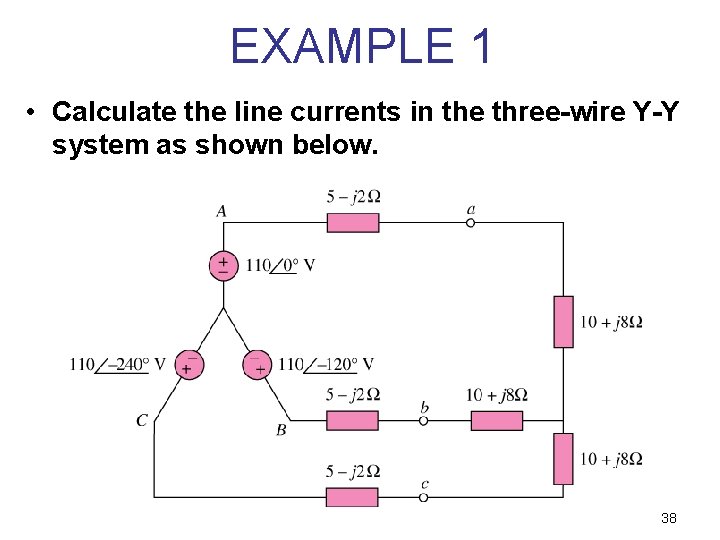
EXAMPLE 1 • Calculate the line currents in the three-wire Y-Y system as shown below. 38

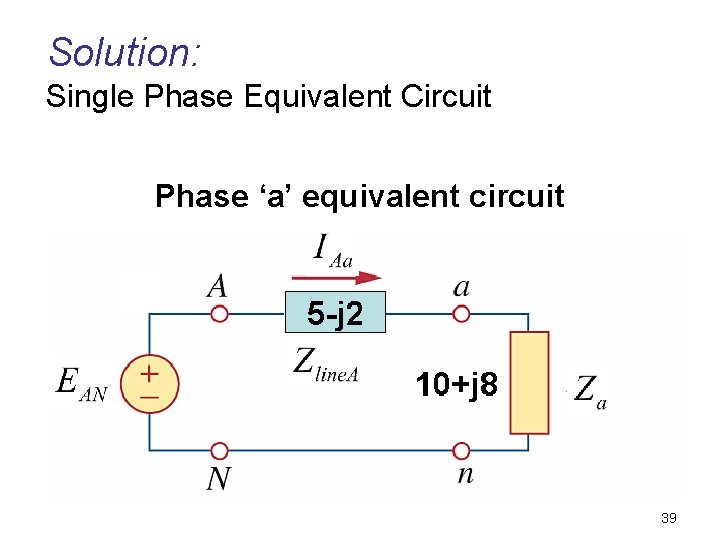
Solution: Single Phase Equivalent Circuit Phase ‘a’ equivalent circuit 39

40

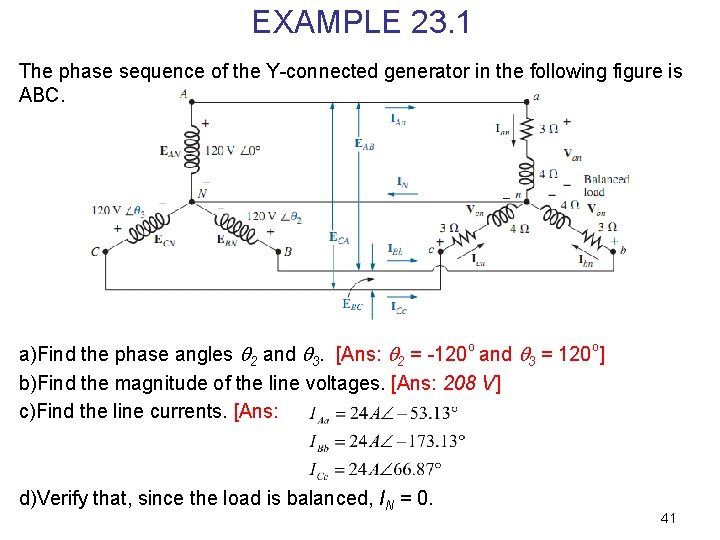
EXAMPLE 23. 1 The phase sequence of the Y-connected generator in the following figure is ABC. a)Find the phase angles 2 and 3. [Ans: 2 = -120 o and 3 = 120 o] b)Find the magnitude of the line voltages. [Ans: 208 V] c)Find the line currents. [Ans: d)Verify that, since the load is balanced, IN = 0. 41

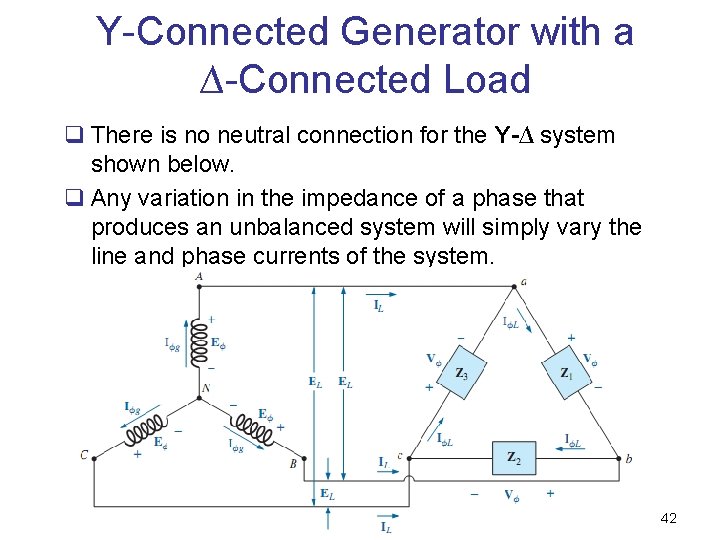
Y-Connected Generator with a ∆-Connected Load q There is no neutral connection for the Y-∆ system shown below. q Any variation in the impedance of a phase that produces an unbalanced system will simply vary the line and phase currents of the system. 42

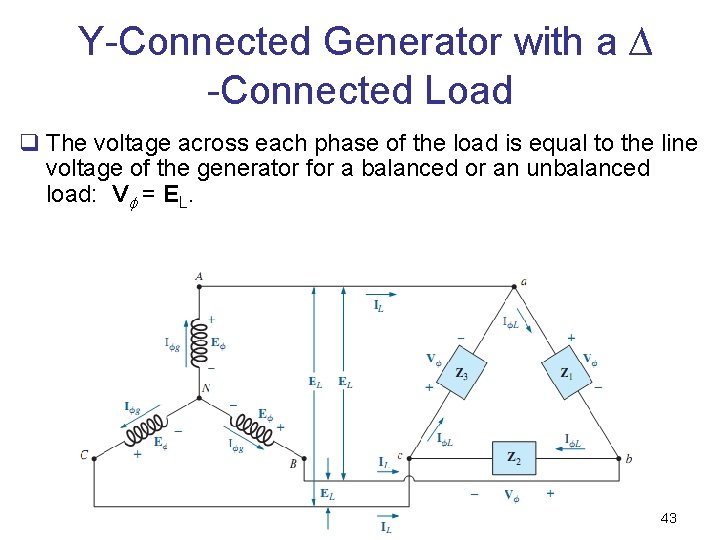
Y-Connected Generator with a ∆ -Connected Load q The voltage across each phase of the load is equal to the line voltage of the generator for a balanced or an unbalanced load: V = EL. 43

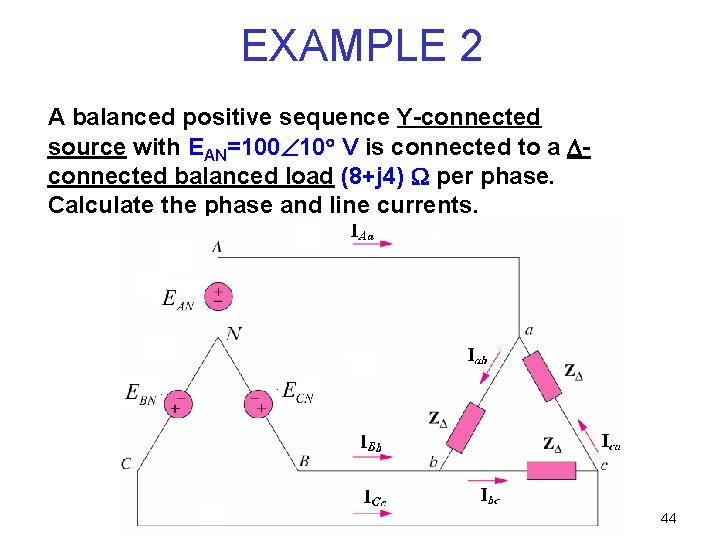
EXAMPLE 2 A balanced positive sequence Y-connected source with EAN=100 10 V is connected to a connected balanced load (8+j 4) per phase. Calculate the phase and line currents. 44

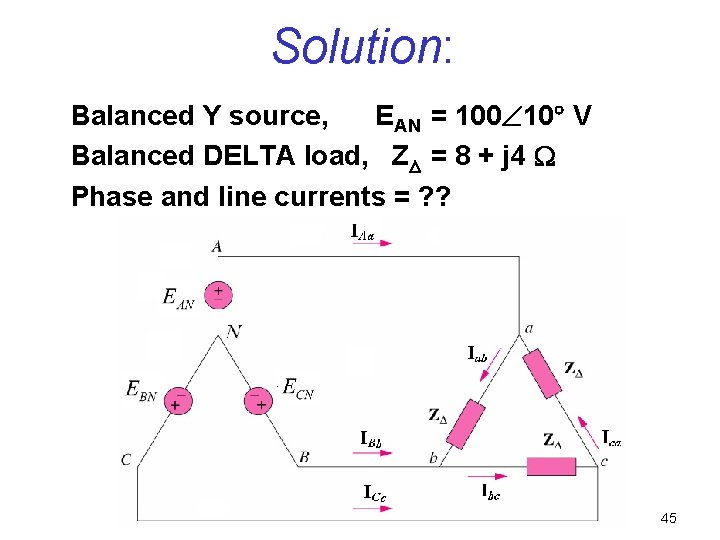
Solution: Balanced Y source, EAN = 100 10 V Balanced DELTA load, Z = 8 + j 4 Phase and line currents = ? ? 45

Phase Currents 46

Phase Currents 47

Line Currents 48

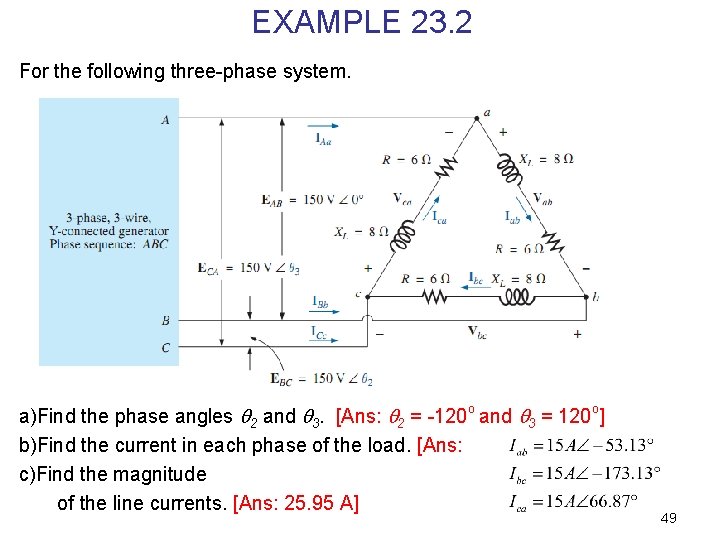
EXAMPLE 23. 2 For the following three-phase system. a)Find the phase angles 2 and 3. [Ans: 2 = -120 o and 3 = 120 o] b)Find the current in each phase of the load. [Ans: c)Find the magnitude of the line currents. [Ans: 25. 95 A] 49

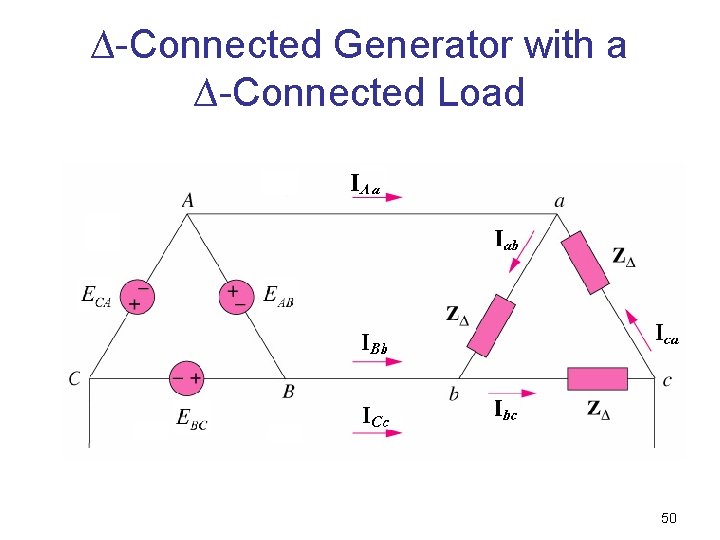
∆-Connected Generator with a ∆-Connected Load 50

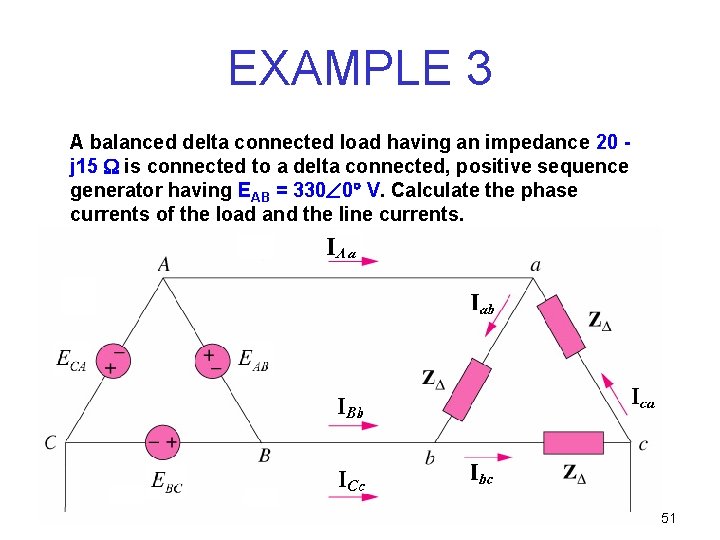
EXAMPLE 3 A balanced delta connected load having an impedance 20 j 15 is connected to a delta connected, positive sequence generator having EAB = 330 0 V. Calculate the phase currents of the load and the line currents. 51

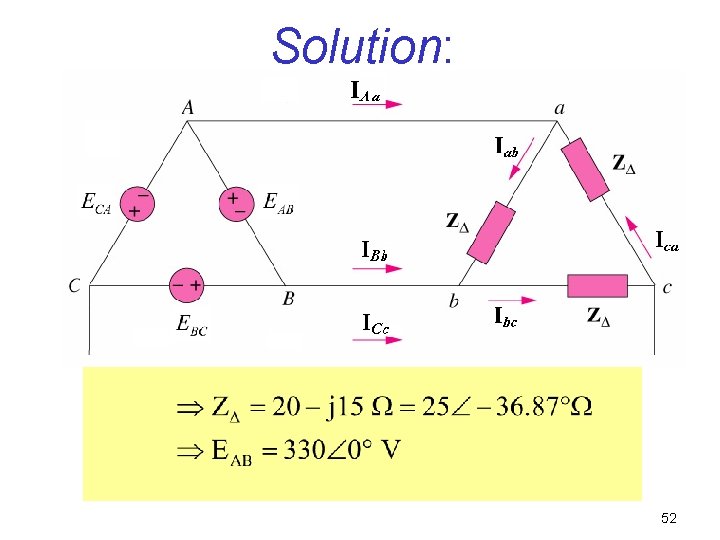
Solution: 52

Phase Currents 53

Line Currents 54

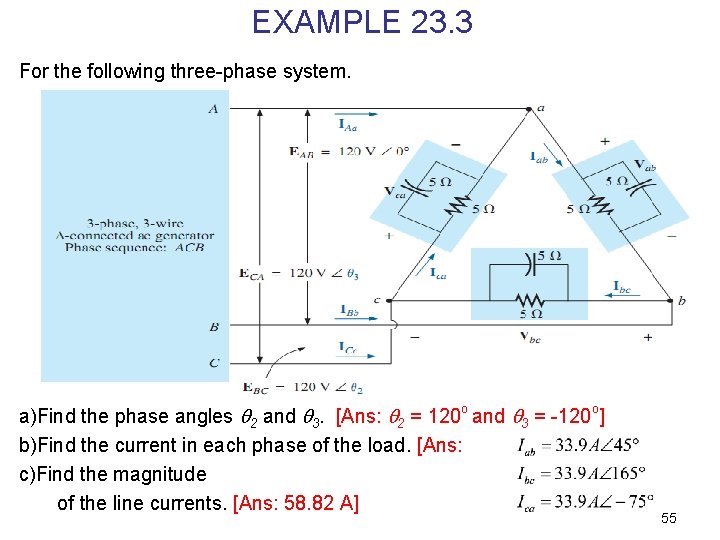
EXAMPLE 23. 3 For the following three-phase system. a)Find the phase angles 2 and 3. [Ans: 2 = 120 o and 3 = -120 o] b)Find the current in each phase of the load. [Ans: c)Find the magnitude of the line currents. [Ans: 58. 82 A] 55

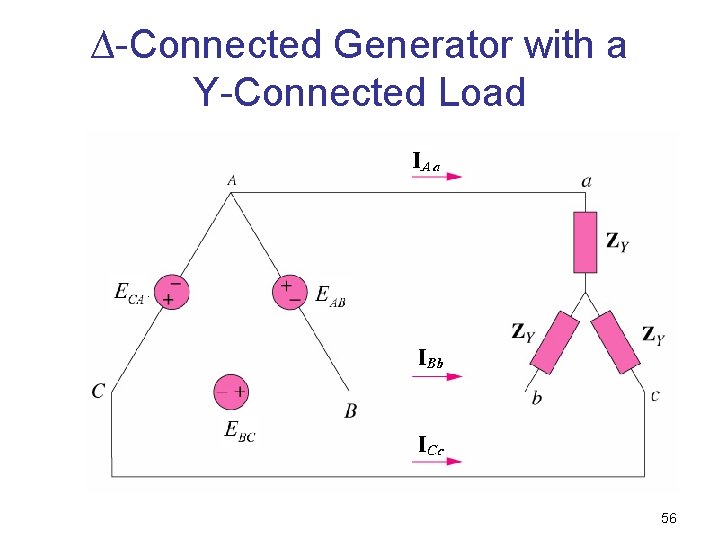
∆-Connected Generator with a Y-Connected Load 56

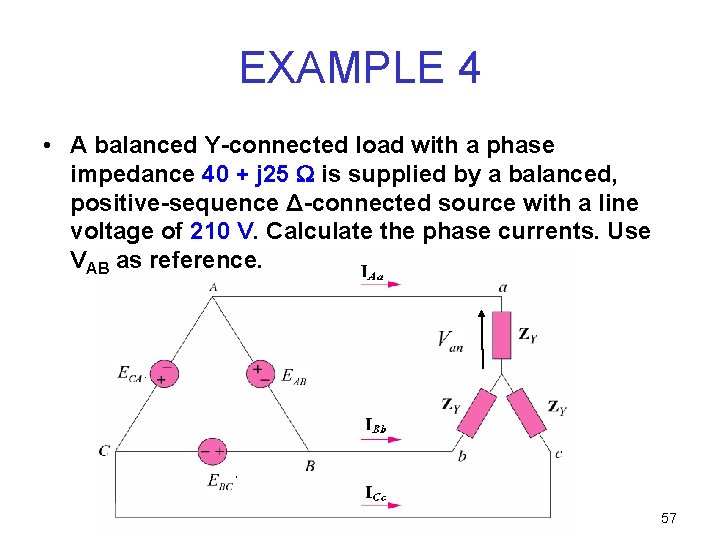
EXAMPLE 4 • A balanced Y-connected load with a phase impedance 40 + j 25 is supplied by a balanced, positive-sequence Δ-connected source with a line voltage of 210 V. Calculate the phase currents. Use VAB as reference. 57

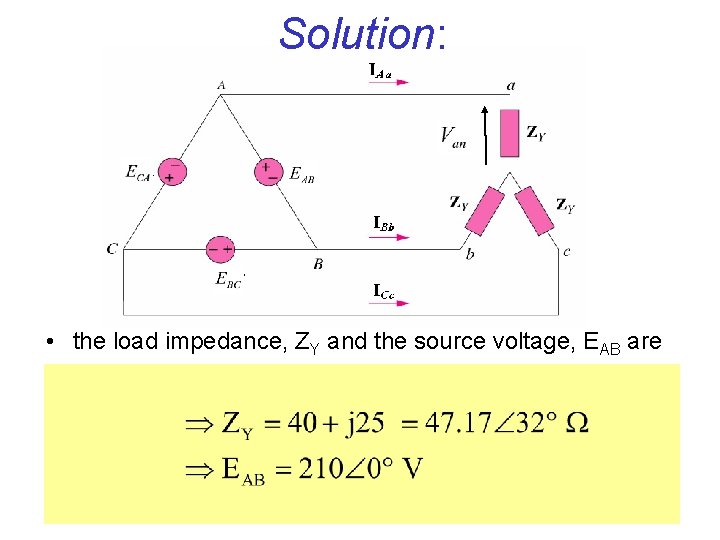
Solution: • the load impedance, ZY and the source voltage, EAB are 58

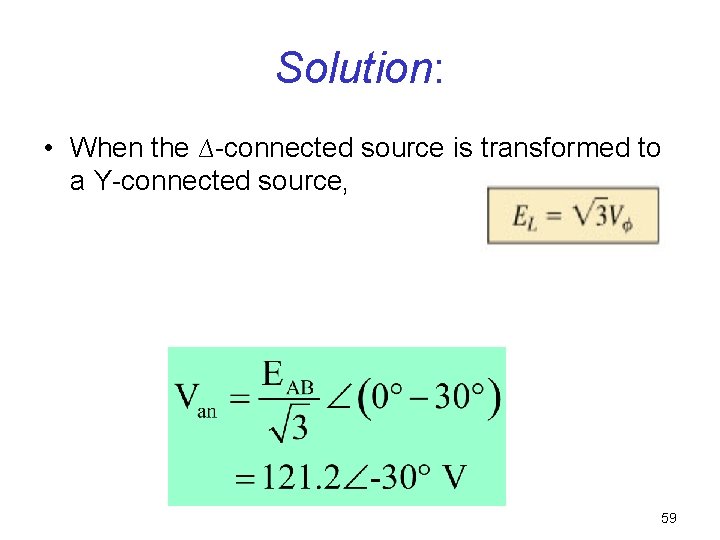
Solution: • When the ∆-connected source is transformed to a Y-connected source, 59

Solution: • The line currents are 60

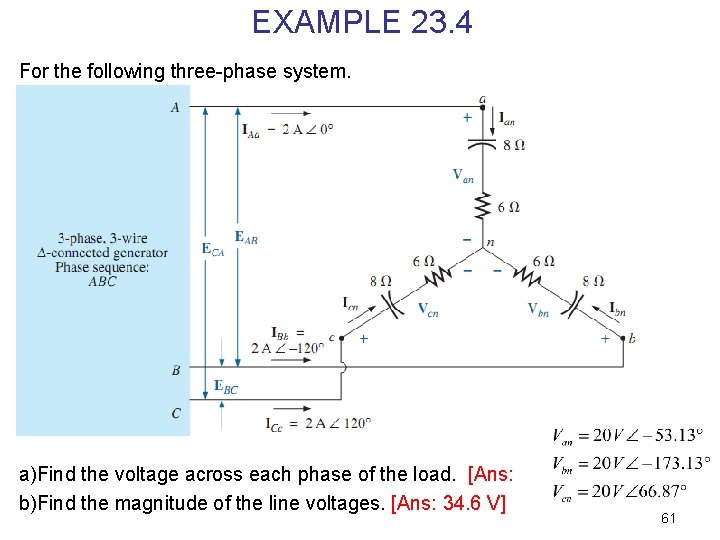
EXAMPLE 23. 4 For the following three-phase system. a)Find the voltage across each phase of the load. [Ans: b)Find the magnitude of the line voltages. [Ans: 34. 6 V] 61

Summary of Relationships in Y and ∆-connections Y-connection Voltage magnitudes Current magnitudes VL leads Vφ by 30° Phase sequence ∆-connection IL lags Iφ by 30° 62