Mathematica Mathematica Palettes Classroom Assistant Mathematica Palettes Classroom

















![Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2] Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-26.jpg)








![Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ] Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-36.jpg)



































![Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2] Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-87.jpg)








![Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ] Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-97.jpg)























































![Solution 1. 기초산술 1) 1234+5678 2) 1234*5678 3) 100/4 4) Plus[1234, 5678] , Times[1234, Solution 1. 기초산술 1) 1234+5678 2) 1234*5678 3) 100/4 4) Plus[1234, 5678] , Times[1234,](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-164.jpg)
![Solution 2. 함수정의 1) f[x_]: = x^2 2) value=Random. Color[] , value: =Random. Color[] Solution 2. 함수정의 1) f[x_]: = x^2 2) value=Random. Color[] , value: =Random. Color[]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-165.jpg)
![Solution 3. Module 1) Module[{x = Range[10]}, x^2 + x] 2) Module[{x = Random. Solution 3. Module 1) Module[{x = Range[10]}, x^2 + x] 2) Module[{x = Random.](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-166.jpg)

![Solution 5. Date 생성 1) Table[5, 10] 2) Table[n + 1, {n, 1, 10}] Solution 5. Date 생성 1) Table[5, 10] 2) Table[n + 1, {n, 1, 10}]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-168.jpg)
![Solution 6. Options 1) List. Plot[Table[x^2 + x, {x, 0, 10}], Plot. Theme -> Solution 6. Options 1) List. Plot[Table[x^2 + x, {x, 0, 10}], Plot. Theme ->](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-169.jpg)

![Solution 8. Manipulate 1) Manipulate[List. Plot[Range[n]], {n, 5, 50, 1}] 2) Manipulate[Column[Table[a, n]], {n, Solution 8. Manipulate 1) Manipulate[List. Plot[Range[n]], {n, 5, 50, 1}] 2) Manipulate[Column[Table[a, n]], {n,](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-171.jpg)
![Solution 9. 대학수학 1) Limit[(x^2+5^x)/(x^2+2 x), x->0] Plot[(x^2+5 x)/(x^2+2 x), {x, -2, 2}] 2) Solution 9. 대학수학 1) Limit[(x^2+5^x)/(x^2+2 x), x->0] Plot[(x^2+5 x)/(x^2+2 x), {x, -2, 2}] 2)](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-172.jpg)
- Slides: 172

Mathematica














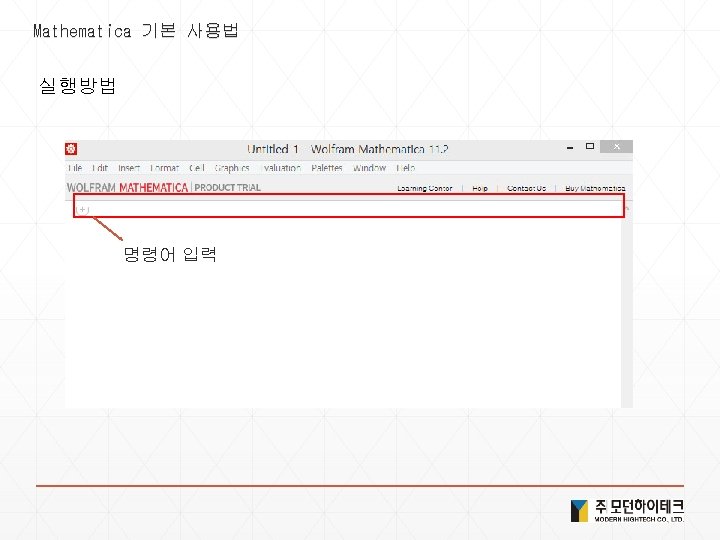
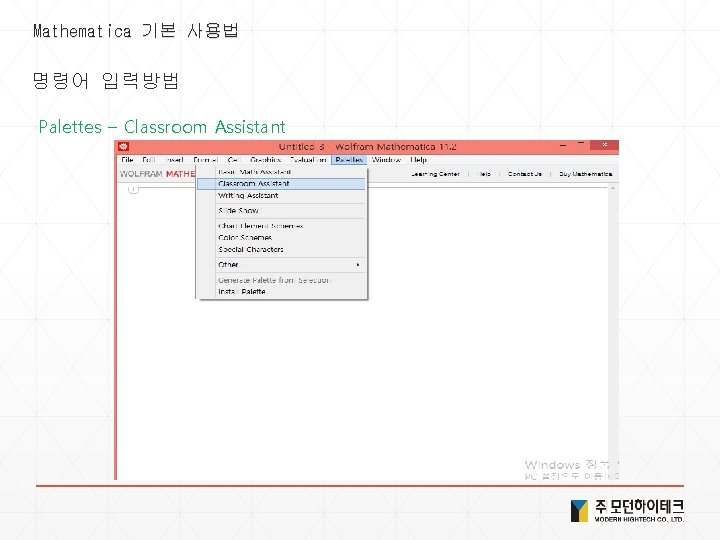
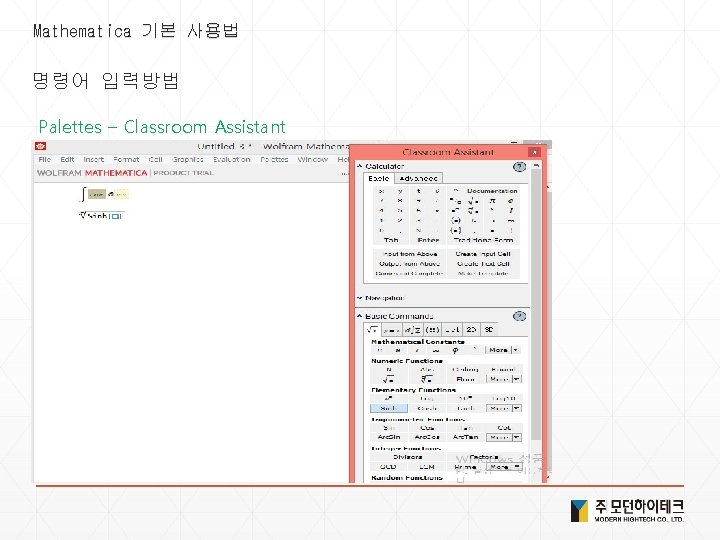
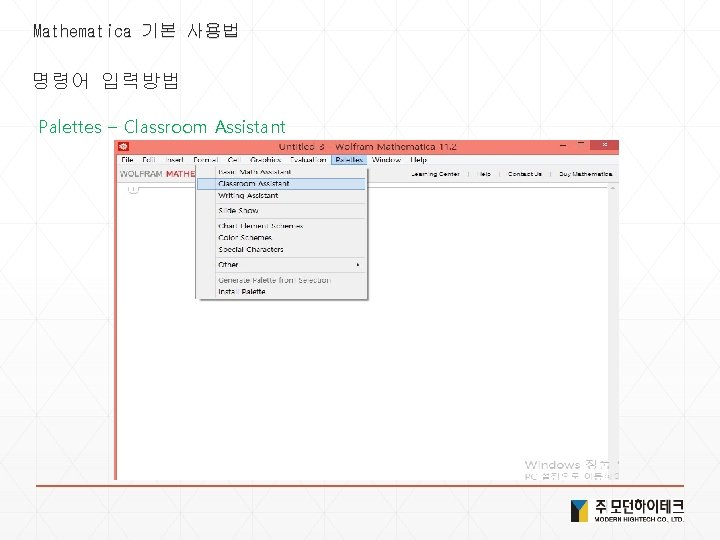
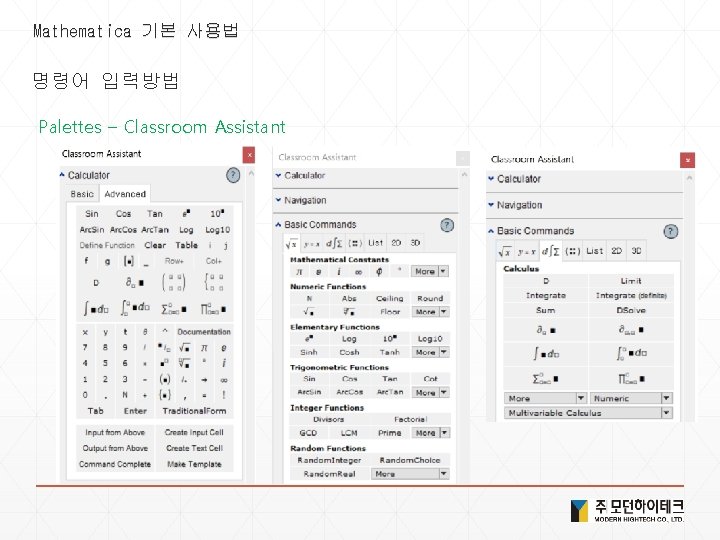
Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant

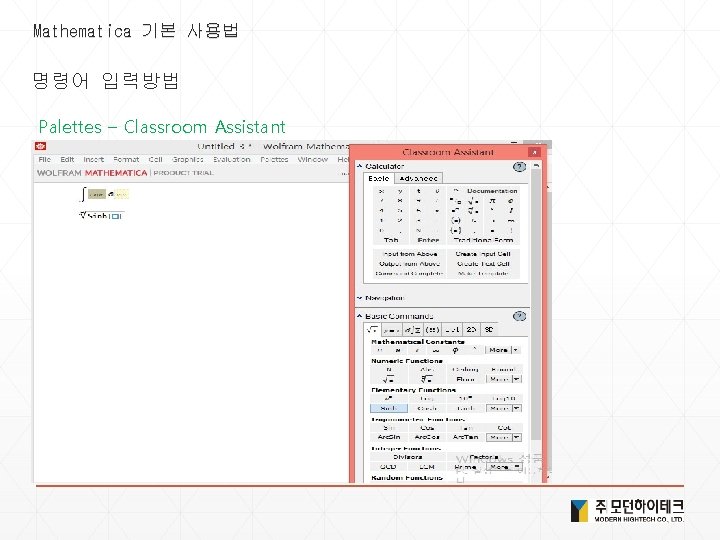
Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant

Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant


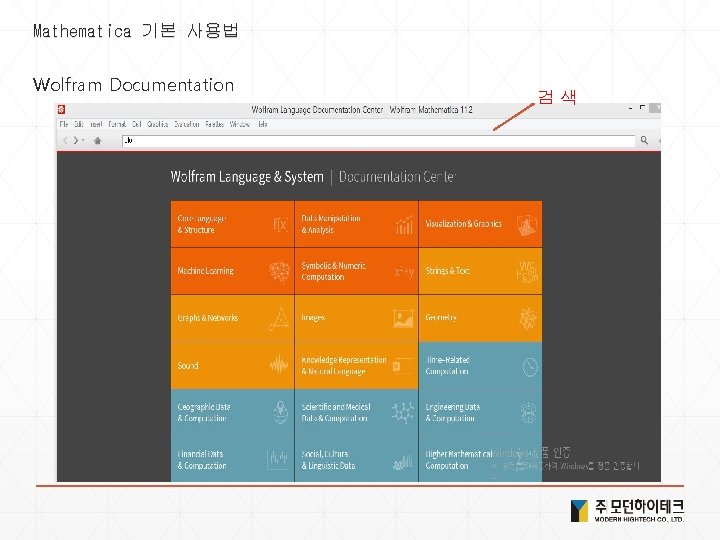
Mathematica 기본 사용법 Wolfram Documentation 검 색

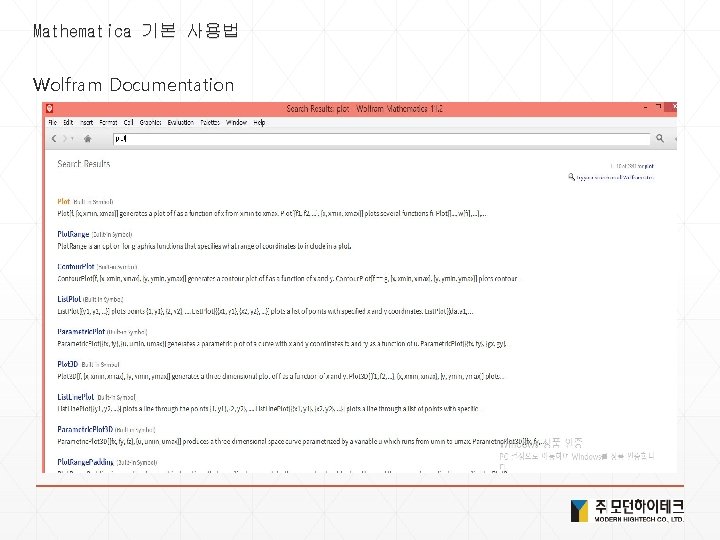
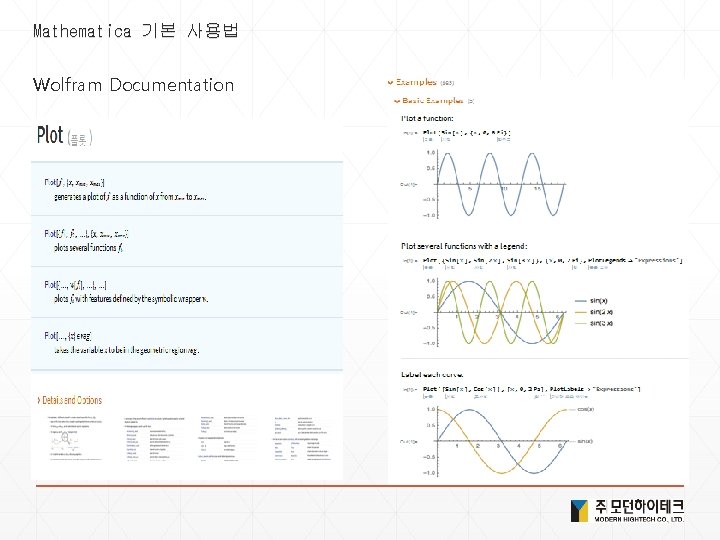
Mathematica 기본 사용법 Wolfram Documentation

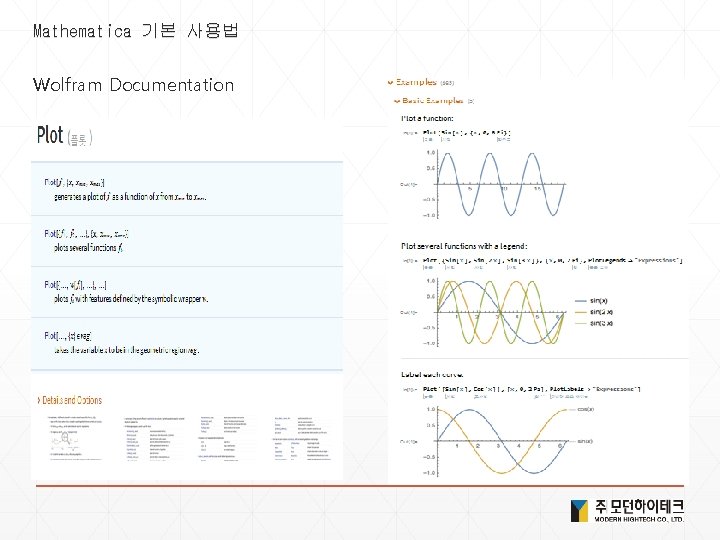
Mathematica 기본 사용법 Wolfram Documentation

Mathematica 기본이론 소개



![Mathematica 기본이론 Note Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다 22 Plus2 2 Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-26.jpg)
Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2] 5 -2 : Subtract[5, 2] 2*3 : Times[2, 3] 6/2 : Divide[6, 2] 3^2 : Power[3, 2] 최대값 : Max[3, 4] 최소값 : Min[3, 4] 무작위 자연수 : Random. Interger[ ]









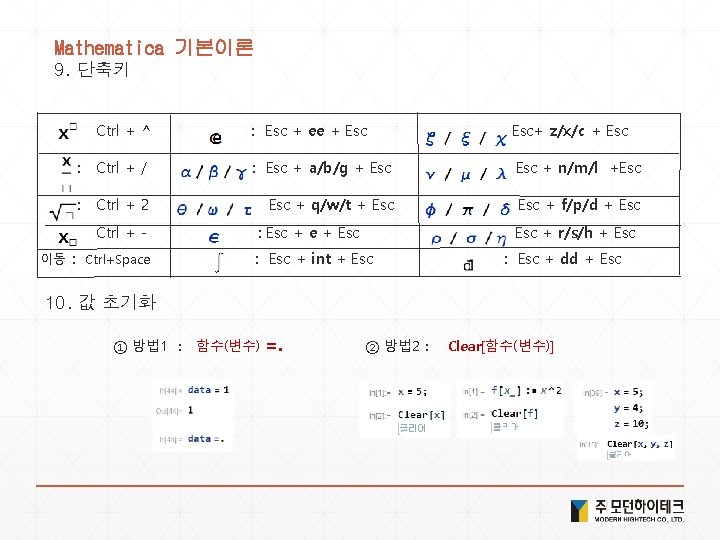
Mathematica 기본이론 9. 단축키 : Ctrl + ^ : Esc + ee + Esc : Esc+ z/x/c + Esc : Ctrl + / : Esc + a/b/g + Esc : Esc + n/m/l +Esc : Ctrl + 2 : Esc + q/w/t + Esc : Esc + f/p/d + Esc : Ctrl + - : Esc + e + Esc : Esc + r/s/h + Esc : Esc + int + Esc : Esc + dd + Esc 이동 : Ctrl+Space 10. 값 초기화 ① 방법 1 : 함수(변수) =. ② 방법 2 : Clear[함수(변수)]
![Mathematica 기본이론 11 N 수치계산 NSolve Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-36.jpg)
Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]


Mathematica 기본이론 13. Import / Export * Import

Mathematica 기본이론 13. Import / Export * Export


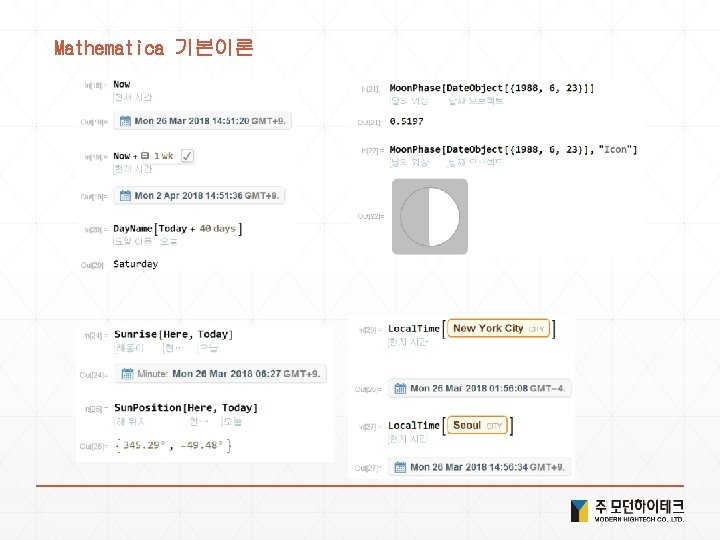
Mathematica 기본이론

Mathematica 기본이론

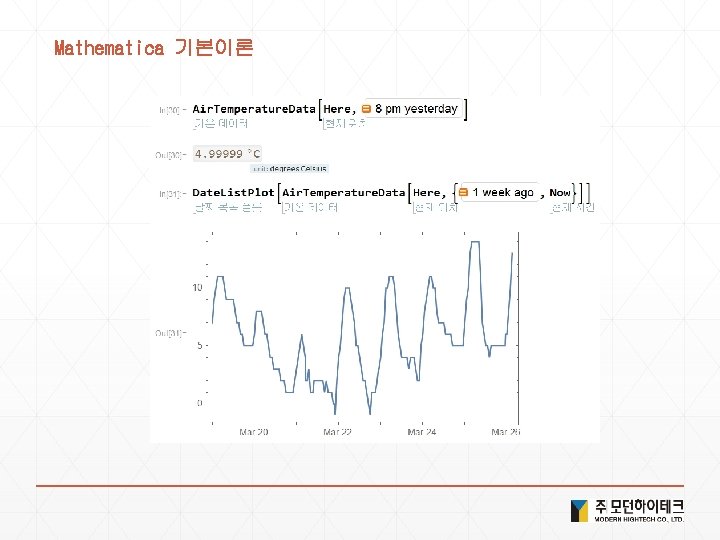
Mathematica 기본이론

Mathematica 기본이론

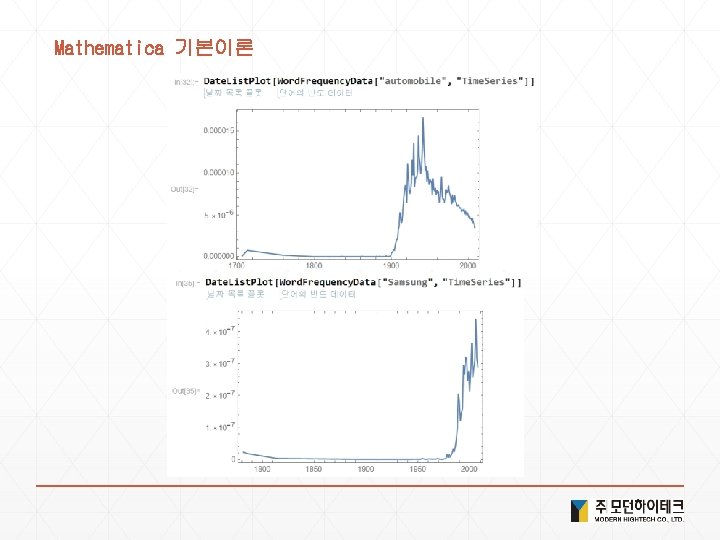
Mathematica 기본이론

Mathematica 기본이론








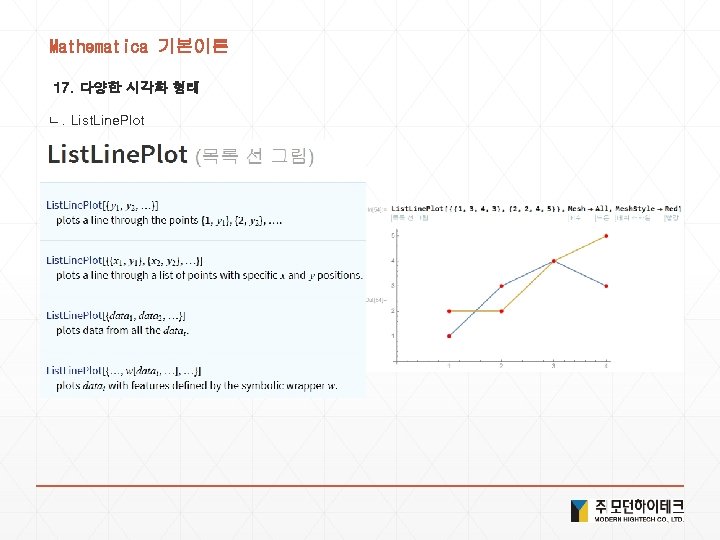
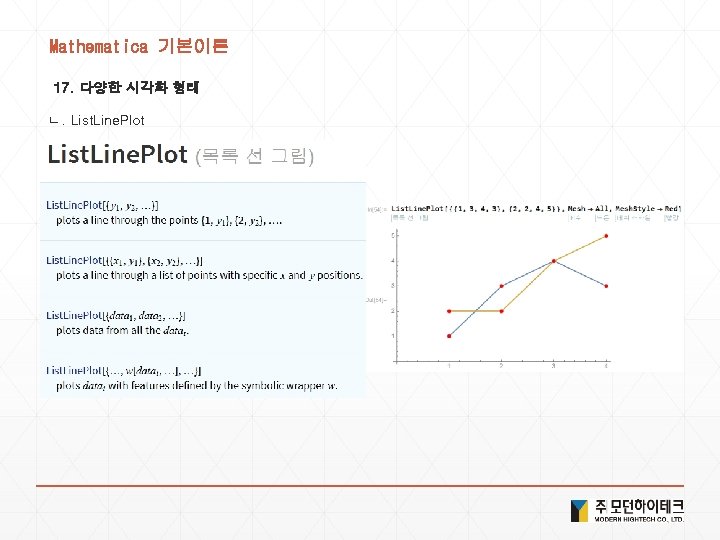
Mathematica 기본이론 17. 다양한 시각화 형태 ㄴ. List. Line. Plot

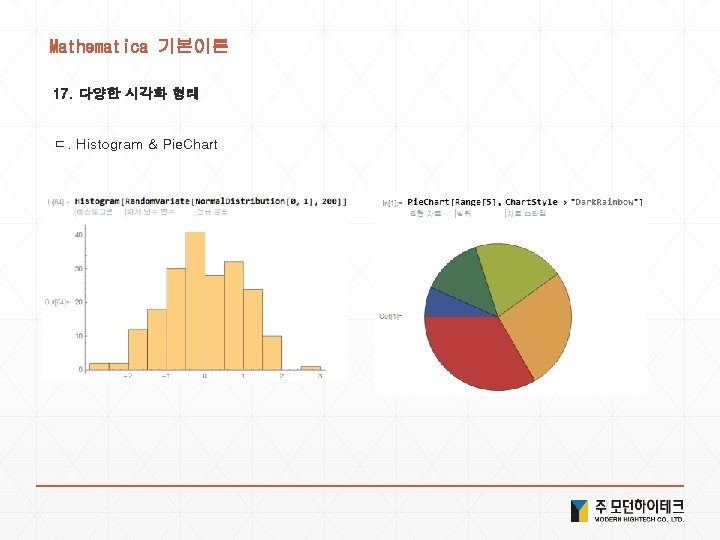
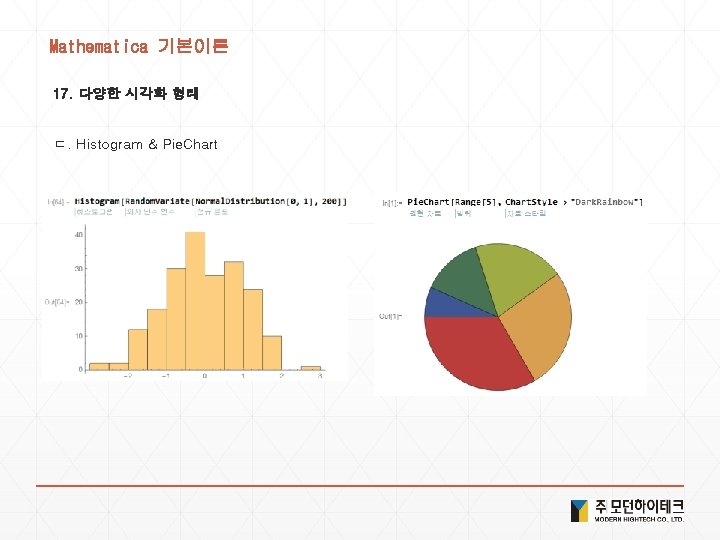
Mathematica 기본이론 17. 다양한 시각화 형태 ㄷ. Histogram & Pie. Chart

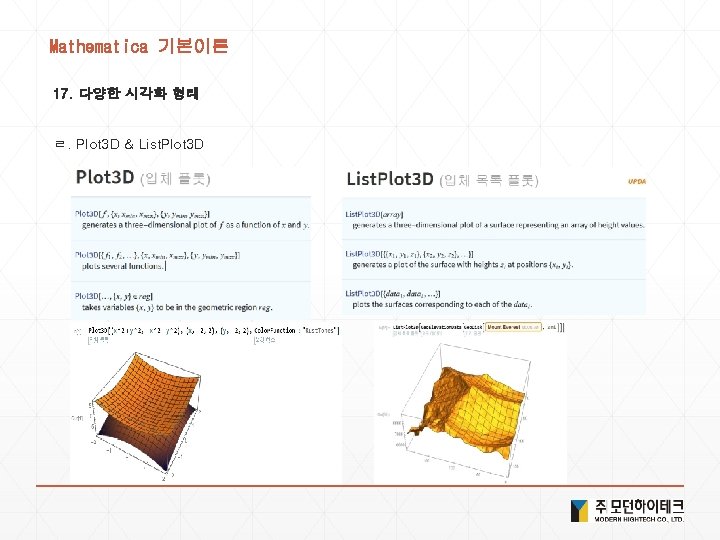
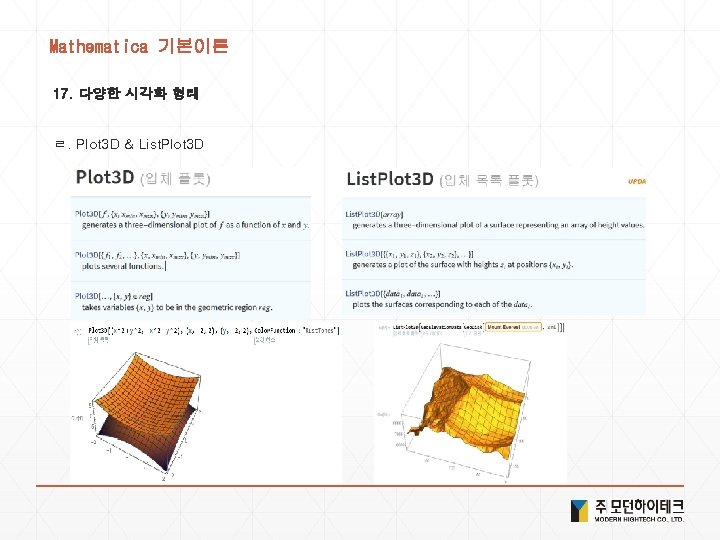
Mathematica 기본이론 17. 다양한 시각화 형태 ㄹ. Plot 3 D & List. Plot 3 D

Mathematica 기본이론 17. 다양한 시각화 형태 ㅁ. Graphics & Graphics 3 D



















Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant

Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant

Mathematica 기본 사용법 명령어 입력방법 Palettes – Classroom Assistant


Mathematica 기본 사용법 Wolfram Documentation 검 색

Mathematica 기본 사용법 Wolfram Documentation

Mathematica 기본 사용법 Wolfram Documentation

Mathematica 기본이론 실습



![Mathematica 기본이론 Note Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다 22 Plus2 2 Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-87.jpg)
Mathematica 기본이론 -Note- Wolfram 언어의 사칙연산 함수를 통해서도 계산이 가능하다. 2+2 : Plus[2, 2] 5 -2 : Subtract[5, 2] 2*3 : Times[2, 3] 6/2 : Divide[6, 2] 3^2 : Power[3, 2] 최대값 : Max[3, 4] 최소값 : Min[3, 4] 무작위 자연수 : Random. Interger[ ]









Mathematica 기본이론 9. 단축키 : Ctrl + ^ : Esc + ee + Esc : Esc+ z/x/c + Esc : Ctrl + / : Esc + a/b/g + Esc : Esc + n/m/l +Esc : Ctrl + 2 : Esc + q/w/t + Esc : Esc + f/p/d + Esc : Ctrl + - : Esc + e + Esc : Esc + r/s/h + Esc : Esc + int + Esc : Esc + dd + Esc 이동 : Ctrl+Space 10. 값 초기화 ① 방법 1 : 함수(변수) =. ② 방법 2 : Clear[함수(변수)]
![Mathematica 기본이론 11 N 수치계산 NSolve Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-97.jpg)
Mathematica 기본이론 11. N[ ] : 수치계산 / NSolve[ ]


Mathematica 기본이론 13. Import / Export * Import

Mathematica 기본이론 13. Import / Export * Export


Mathematica 기본이론

Mathematica 기본이론

Mathematica 기본이론

Mathematica 기본이론

Mathematica 기본이론

Mathematica 기본이론








Mathematica 기본이론 17. 다양한 시각화 형태 ㄴ. List. Line. Plot

Mathematica 기본이론 17. 다양한 시각화 형태 ㄷ. Histogram & Pie. Chart

Mathematica 기본이론 17. 다양한 시각화 형태 ㄹ. Plot 3 D & List. Plot 3 D

Mathematica 기본이론 17. 다양한 시각화 형태 ㅁ. Graphics & Graphics 3 D
















Mathematica 예제실습














* Mathematica 학습 추천 사이트 - http: //www. wolfram. com/mathematica ( Mathematica 사이트 ) - http: //demonstrations. wolfram. com/index. php (각종 학습소스) - http: //www. wolfram. com/wolfram-u/ (학습영상) - http: //community. wolfram. com/? source=footer (커뮤니티 게시판-Q&A)



S o l u t i o n






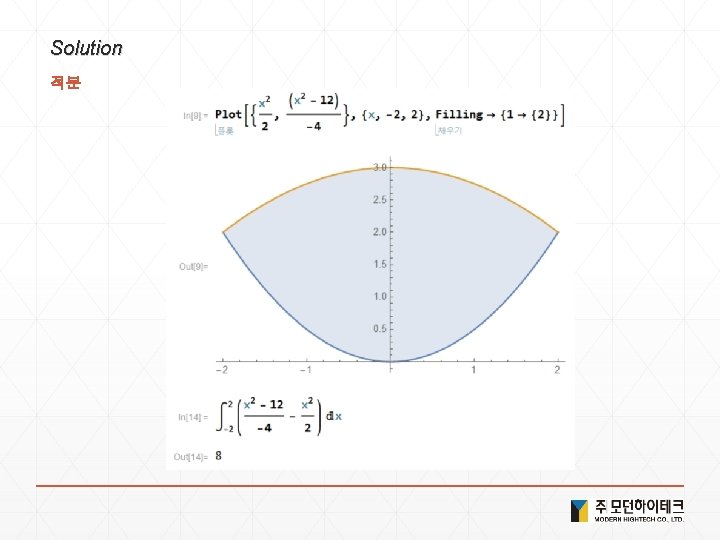
Solution 적분






![Solution 1 기초산술 1 12345678 2 12345678 3 1004 4 Plus1234 5678 Times1234 Solution 1. 기초산술 1) 1234+5678 2) 1234*5678 3) 100/4 4) Plus[1234, 5678] , Times[1234,](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-164.jpg)
Solution 1. 기초산술 1) 1234+5678 2) 1234*5678 3) 100/4 4) Plus[1234, 5678] , Times[1234, 5678] , Divide[100, 4] 5) Random. Integer[100] 6) 5^2 7) 3^(7*8)
![Solution 2 함수정의 1 fx x2 2 valueRandom Color value Random Color Solution 2. 함수정의 1) f[x_]: = x^2 2) value=Random. Color[] , value: =Random. Color[]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-165.jpg)
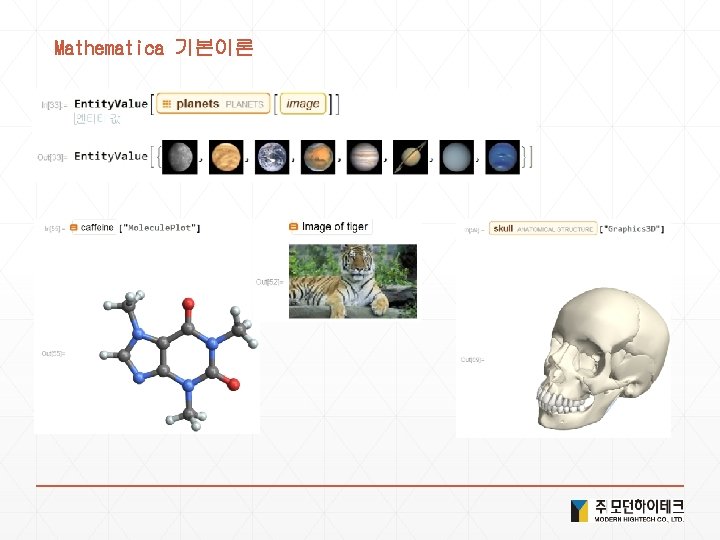
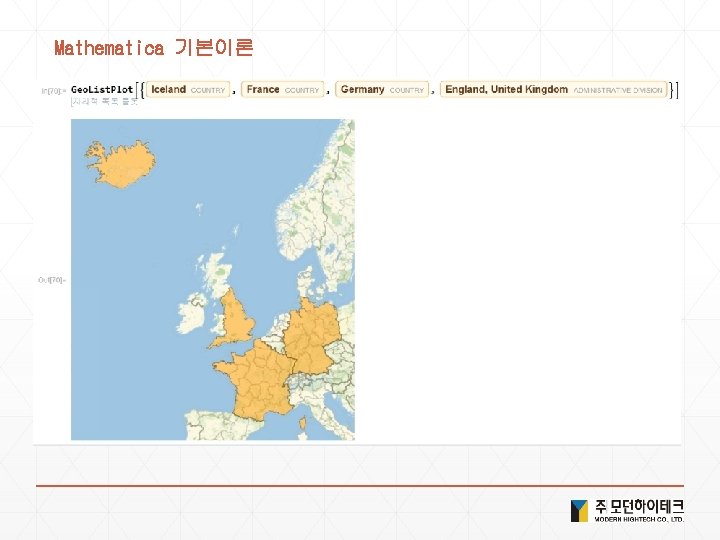
Solution 2. 함수정의 1) f[x_]: = x^2 2) value=Random. Color[] , value: =Random. Color[] 3) Color. Negate @ Edge. Detect @ 사진 4) 사진 // Edge. Detect // Color. Negate 5) Framed /@ {x, y, z} 6) Color. Negate /@ Entity. Value[ <Ctrl+ = planets> , "Image" ] 7) Map[Framed, {x, y, z}] 8) f[x_, y_] : = (x*y)/(x + y) 9) f[{a_, b_}] : = {a + b, a - b, a*b} 10) x//d//c//b//a 11) Framed /@ Alphabet[] 12) Map[Framed, Alphabet[]] 13) Geo. Graphics /@ Entity. List[ <Ctrl+ = countries in G 5> ] 14) Map[Geo. Graphics, Entity. List[ <Ctrl+ = countries in G 5> ]
![Solution 3 Module 1 Modulex Range10 x2 x 2 Modulex Random Solution 3. Module 1) Module[{x = Range[10]}, x^2 + x] 2) Module[{x = Random.](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-166.jpg)
Solution 3. Module 1) Module[{x = Range[10]}, x^2 + x] 2) Module[{x = Random. Integer[100, 10]}, Column[{x, Sort[x], Max[x], Total[x]}]] 3) Module[{x = Range[10], n = 2}, x^n] 4) Module[{x, y}, x = Range[10]; y = x^2 ; y = y + 10000]

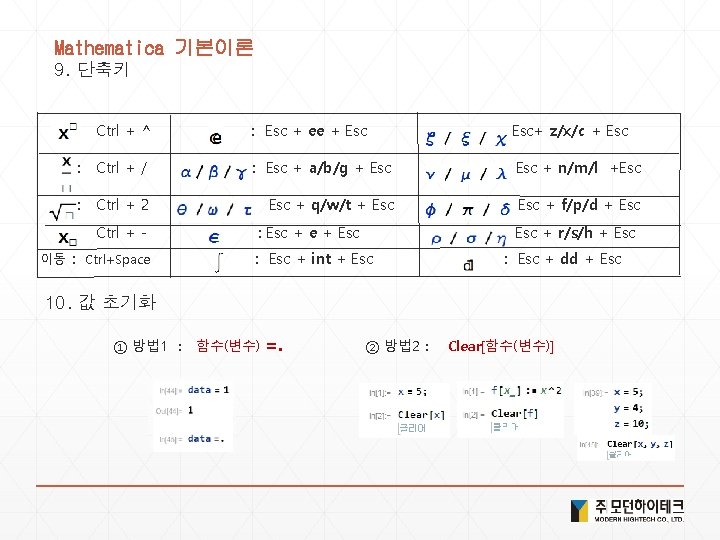
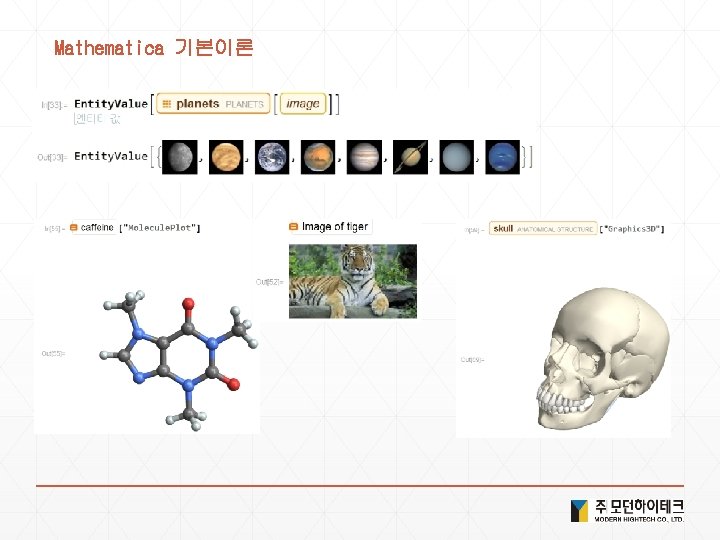
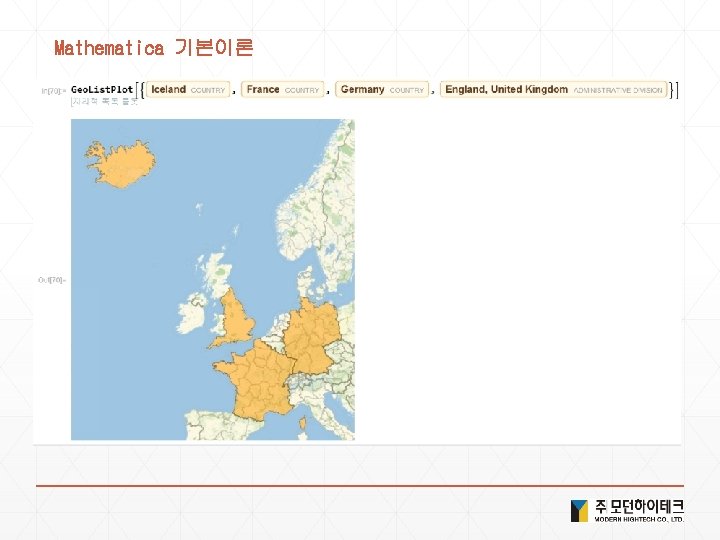
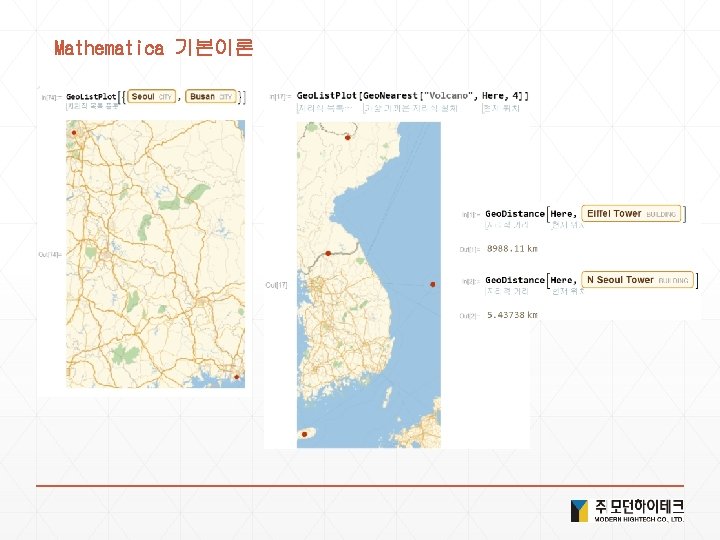
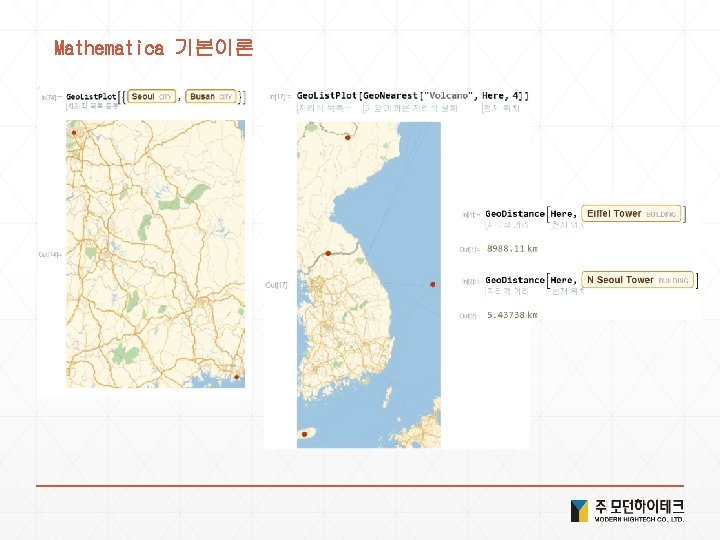
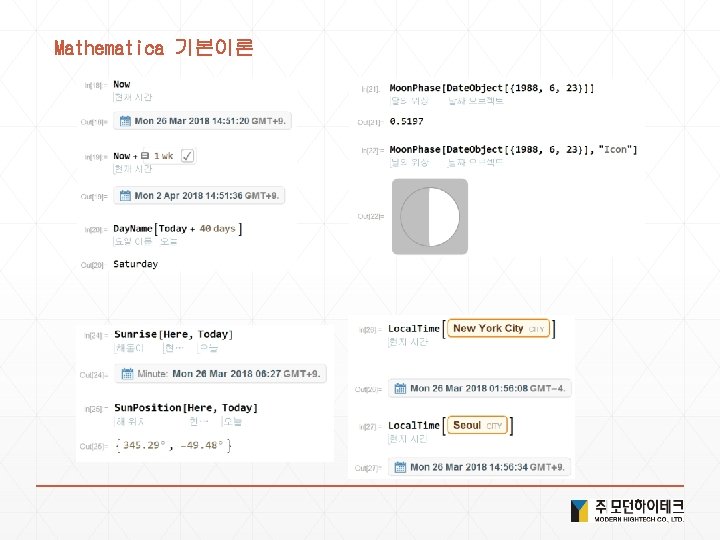
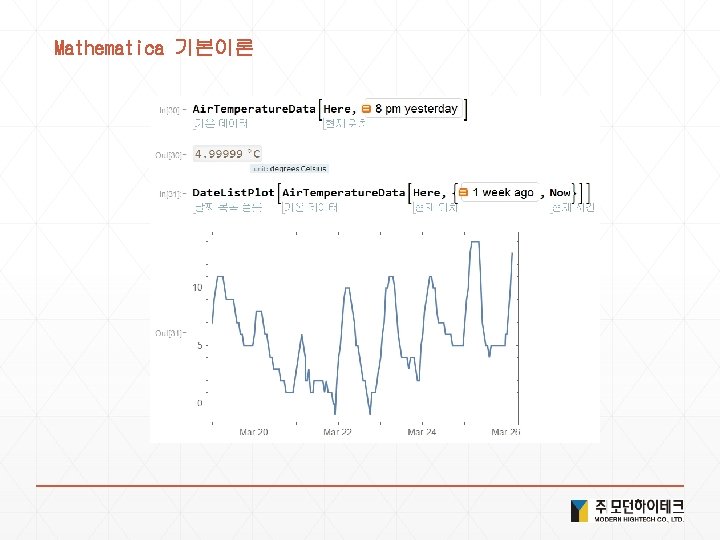
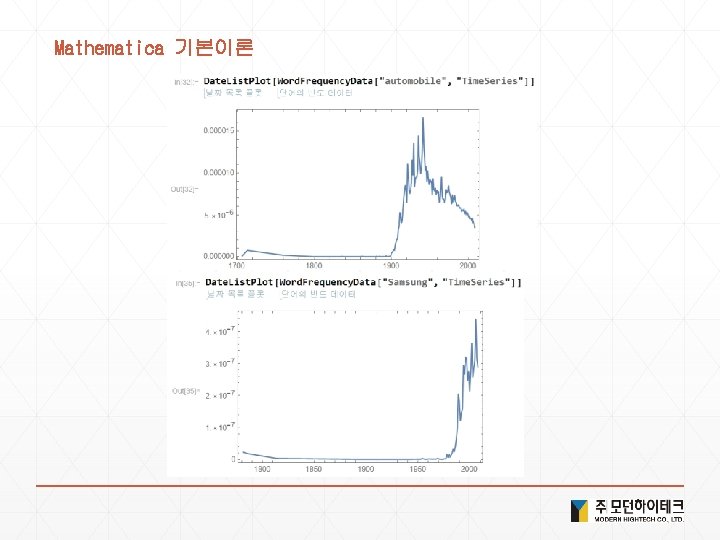
Solution 4. 현실세계 데이터 1) <Ctrl+ = flag of USA > or <Ctrl+ = USA >["Flag"] 2) <Ctrl+ = Bordering. Countries of USA> or <Ctrl+ = USA >["Bordering. Countries"] 3) <Ctrl+ =image of elephant > or <Ctrl+ = elephant >["Image"] 4) Image. Collage[Entity. Value[ <Ctrl+ = planets> , "Image"] 5) <Ctrl+ = Height of Empire State Building > or <Ctrl+ = Empire State Building >["Height"] 6) Geo. List. Plot[{ <Ctrl+ =Seoul > , <Ctrl+ = Incheon > , <Ctrl+ = Suwon > }] 7) Geo. Distance[ <Ctrl+ = New York> , <Ctrl+ = london> ] 8) Geo. Graphics[ <Ctrl+ = China> 9) Geo. Graphics[Geo. Path[{ <Ctrl+ = China> , <Ctrl+ = Japan>}]] 10) Day. Name[ <Ctrl+ = January 1 , 2000> ] 11) Local. Time[<Ctrl+ = Seoul>] 12) Sunset[Here, Today] - Sunrise[Here, Today] 13) Date. List. Plot[Word. Frequency. Data[{"gasoline", "hybrid"}, "Time. Series"]]
![Solution 5 Date 생성 1 Table5 10 2 Tablen 1 n 1 10 Solution 5. Date 생성 1) Table[5, 10] 2) Table[n + 1, {n, 1, 10}]](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-168.jpg)
Solution 5. Date 생성 1) Table[5, 10] 2) Table[n + 1, {n, 1, 10}] 3) Table[Random. Integer[10], 20] 4) Table[2 n + 1, {n, 0, 49}] 5) Bar. Chart[Table[n^2, {n, 1, 10}]] 6) Table[n^2 + 2, {n, 10, 2}] 7) f[x_] : = Sin[x] + Cos[x] Table[f[x], {x, 0, 6 Pi, Pi}]
![Solution 6 Options 1 List PlotTablex2 x x 0 10 Plot Theme Solution 6. Options 1) List. Plot[Table[x^2 + x, {x, 0, 10}], Plot. Theme ->](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-169.jpg)
Solution 6. Options 1) List. Plot[Table[x^2 + x, {x, 0, 10}], Plot. Theme -> "Marketing"] 2) List. Plot[Table[x^2 + x, {x, 0, 10}], Filling -> Axis] 3) List. Plot[Table[x^2 + x, {x, 0, 10}], Background -> Yellow] 4) List. Plot[{1, 3, 2, 5, 4}, Plot. Range -> {{-1, 6}, {-1, 6}}] 5) Plot[{Sin[x], Sin[2 x], Sin[3 x]}, {x, 0, 2 Pi}, Plot. Style -> {{RGBColor[0. 5, 0. 5], RGBColor[0. 83, 0. 5], RGBColor[0. 5, 0. 16, 0. 5]}, Thickness[0. 01]}, Frame -> True]

Solution 7. 다양한 시각화 형태 1) List. Line. Plot[Table[x^n, {n, 2, 4}, {x, 1, 10}]] 2) List. Line. Plot[Table[Prime[n], {n, 20}], Filling -> Axis, Mesh -> True, Mesh. Style -> Red] 3) f[x_, y_] : = Sin[x + y^2] Plot 3 D[f[x, y], {x, -3, 3}, {y, -2, 2}] 4) List. Plot 3 D[Geo. Elevation. Data[Geo. Disk[ <Ctrl+ = mount fuji>]]] 5) f[x_] : = Sin[x] + Random[Real, {0. 03, 0. 3}] List. Plot[Table[f[x], {x, 0, 6 Pi, Pi/50}]] 6) Histogram[Table[Prime[n + 1] - Prime[n], {n, 10000}]] 7) Pie. Chart[{2, 3, 5}, Chart. Labels -> {"a", "b", "c"}, Chart. Legends -> {"a", "b", "c"}] 8) Graphics[Regular. Polygon[5]] 9) Graphics 3 D[Cone[]] 10) Parametric. Plot 3 D[{x, y, x^2 + y^2}, {x, -2, 2}, {y, -2, 2}] 11) Show[ Plot[x^2 + x, {x, 0, 10}], Plot[x^3, {x, 0, 10}]] 12) Show[ Plot[Cos[x^2/x], {x, 2, 10}], Background -> Yellow, Plot. Range -> {{0, 10}, {-2, 2}}]
![Solution 8 Manipulate 1 ManipulateList PlotRangen n 5 50 1 2 ManipulateColumnTablea n n Solution 8. Manipulate 1) Manipulate[List. Plot[Range[n]], {n, 5, 50, 1}] 2) Manipulate[Column[Table[a, n]], {n,](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-171.jpg)
Solution 8. Manipulate 1) Manipulate[List. Plot[Range[n]], {n, 5, 50, 1}] 2) Manipulate[Column[Table[a, n]], {n, 1, 10, 1}] 3) Manipulate[Graphics[Style[Disk[], Hue[n]]], {n, 0, 1}] 4) Manipulate[Pie. Chart[Table[1, n]], {n, 1, 10, 1}]
![Solution 9 대학수학 1 Limitx25xx22 x x0 Plotx25 xx22 x x 2 2 2 Solution 9. 대학수학 1) Limit[(x^2+5^x)/(x^2+2 x), x->0] Plot[(x^2+5 x)/(x^2+2 x), {x, -2, 2}] 2)](https://slidetodoc.com/presentation_image_h/ae61c604b880f564b0ba75fe3eeec189/image-172.jpg)
Solution 9. 대학수학 1) Limit[(x^2+5^x)/(x^2+2 x), x->0] Plot[(x^2+5 x)/(x^2+2 x), {x, -2, 2}] 2) For[i=0, i<=10, i++, s= ; Print["n=", i , “ -> ", s]] 3). 4) Plot[Floor[x], {x, -1, 5}, Filling->Axis] 5) (*(1) 라플라스변환 *) Laplace. Transform[f''[t]+f[t]==Cos[2 t], t, s] Solve[%, Laplace. Transform[f[t], t, s]] % /. f[0]->0 /. f'[0]->1 Inverse. Laplace. Transform[%, s, t] (*(2) DSolve *) DSolve[{f''[t]+f[t]==Cos[2 t], f[0]==0, f'[0]==1}, f[t], t] %//Simplify