7 Calculus of Residues Residue Theorem a 1

















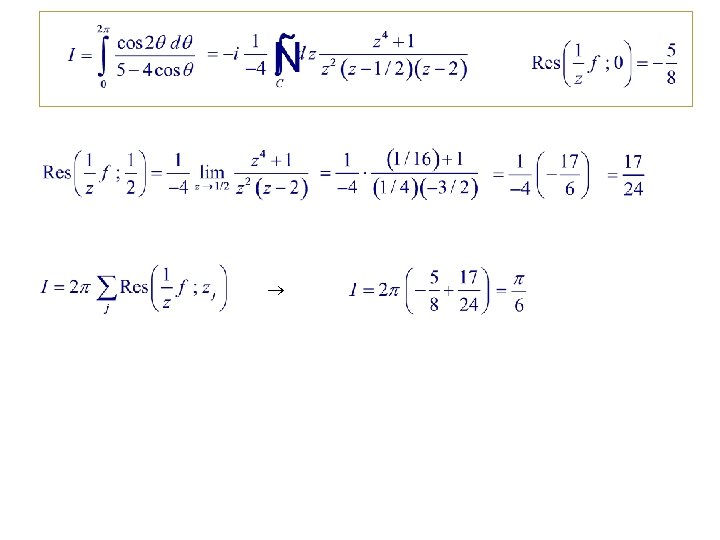




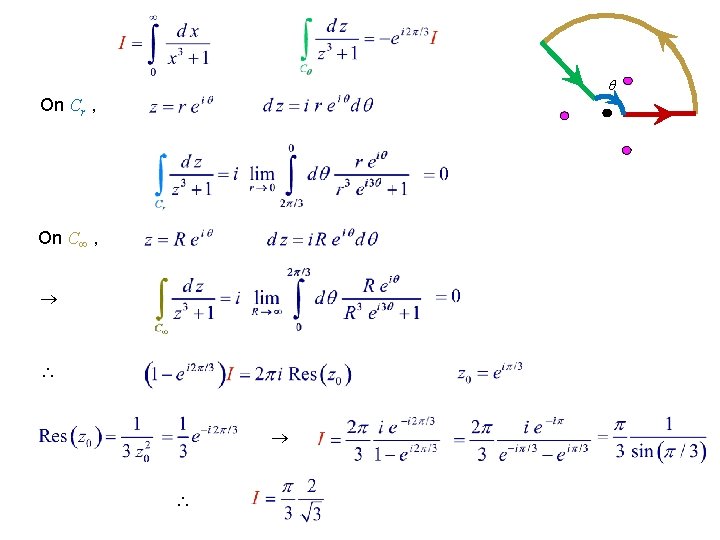











- Slides: 46

7. Calculus of Residues Residue Theorem : a 1 = residue of f at z 0. For a meromorphic function f with n isolated singularities, one can deform C to circumvent them all so that Residue Theorem a 1, i = residue at singularity i.

Computing Residues If f has a simple pole at z 0 , simple poles If f has a pole of order m at z 0 , poles of order m

Example 11. 7. 1. Computing Residues Some examples : Mathematica

Alternatively, z = 0 is a pole of 2 nd order : Mathematica

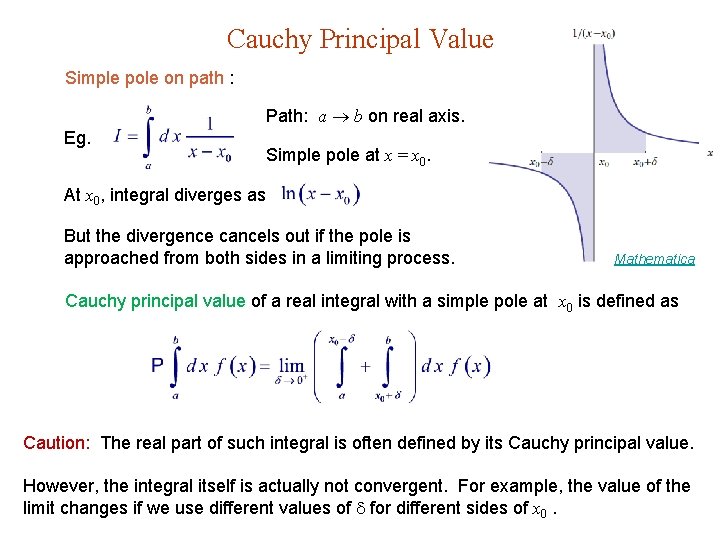
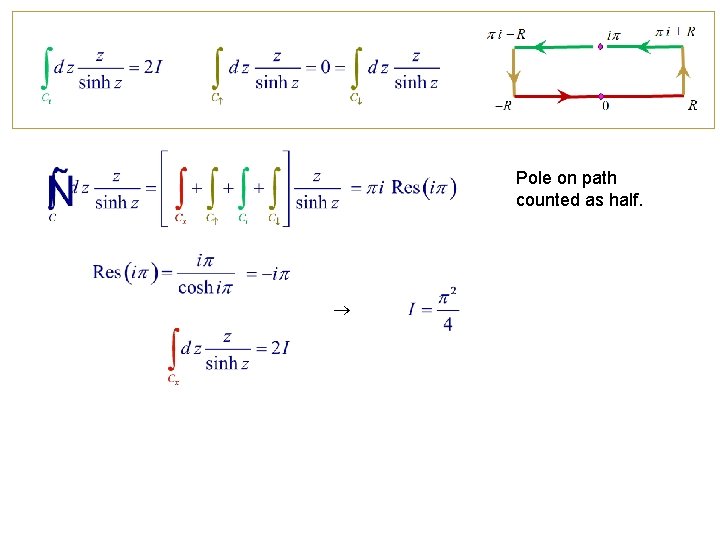
Cauchy Principal Value Simple pole on path : Path: a b on real axis. Eg. Simple pole at x = x 0. At x 0, integral diverges as But the divergence cancels out if the pole is approached from both sides in a limiting process. Mathematica Cauchy principal value of a real integral with a simple pole at x 0 is defined as Caution: The real part of such integral is often defined by its Cauchy principal value. However, the integral itself is actually not convergent. For example, the value of the limit changes if we use different values of for different sides of x 0.

Example 11. 7. 2. A Cauchy Principal Value

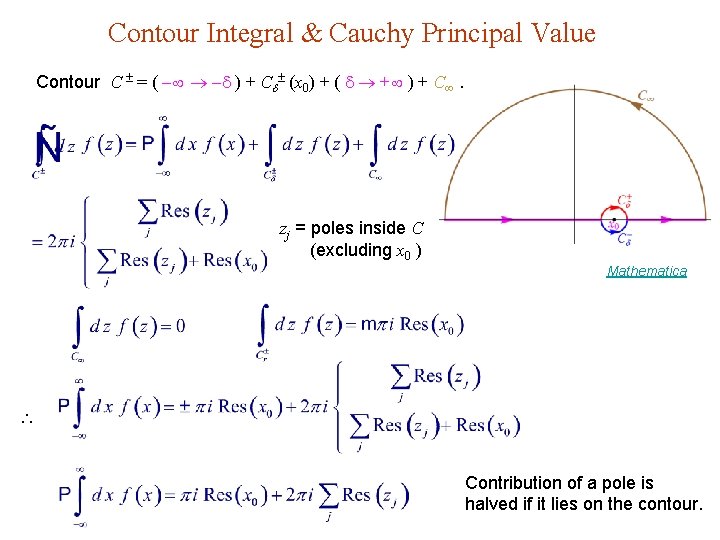
Contour Integral & Cauchy Principal Value Contour C = ( ) + C (x 0) + ( + ) + C . zj = poles inside C (excluding x 0 ) Mathematica Contribution of a pole is halved if it lies on the contour.

Pole Expansion of Meromorphic Functions Expansion of f about 1. A regular point 2. A pole Taylor series. Laurent series. 3. All simple poles (Mittag-Leffler) pole expansion.

Mittag-Leffler Theorem Let f be meromorphic with simple poles at zj 0, (with residue bj) ; j = 1, . . . , M. If for large |z| , then Proof : Consider where CN is a circle centered at w=0, of radius RN, that encloses the 1 st N poles of f closest to w=0. For RN , QED

Example 11. 7. 3. Pole Expansion of tan z poles at Let

Example 11. 7. 4. Pole Expansion of cot z has at z = 0 with residue has poles at Let Similarly

Counting Poles & Zeros Let z 0 be either a pole or zero of f (z). Set where g is regular at z 0. Nf = Sum of the orders of zeros of f enclosed by C. Pf = Sum of the orders of poles of f enclosed by C. if only zero or pole enclosed by C is z 0.

Rouche’s Theorem If f (z) & g(z) are analytic in the region R bounded by C and | f (z) | > | g(z) | on C, then f (z) & f (z) + g(z) have the same number of zeros in R. f (z) & g(z) are analytic Proof : C x = change of x going around C once.

Example 11. 7. 5. Let To find NF for . Counting Zeros Find NF for , let with so that To find NF for on C : |z| = 1 i. e. , , let with so that on C : |z| = 3

Product Expansion of Entire Functions f (z) is an entire function if it is analytic for all finite z. Let f (z) be an entire function. Then is meromorphic (analytic except for poles for all finite z). Poles of F are zeros of f. If the M zeros, zj , of f are all simple (of order 1), then zj are simple poles of F with so that

Ex. 11. 7. 5 Likewise Gamma function

8. Evaluation of Definite Integrals Trigonometric Integrals, Range (0, 2 ) f = rational function & finite everywhere Set C = unit circle at z = 0. zj = poles inside C

Example 11. 8. 1. Integral of cos in Denominator Poles at inside C outside

Example 11. 8. 2. Another Trigonometric Integral Only poles at 0 & ½ are inside C.
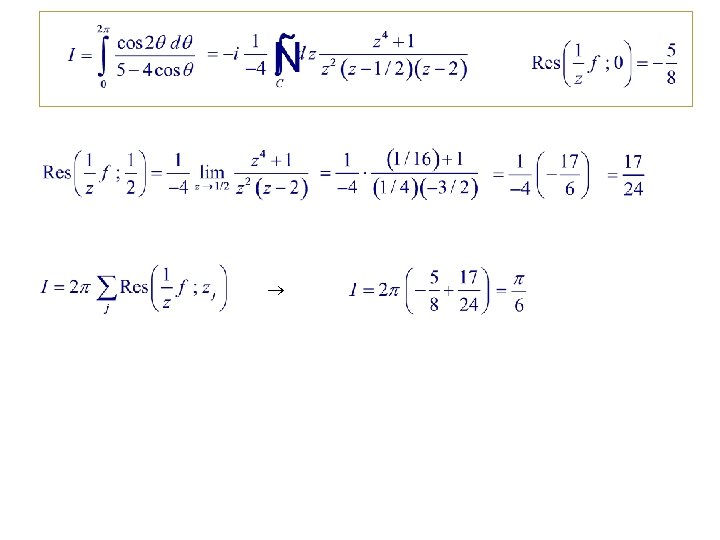

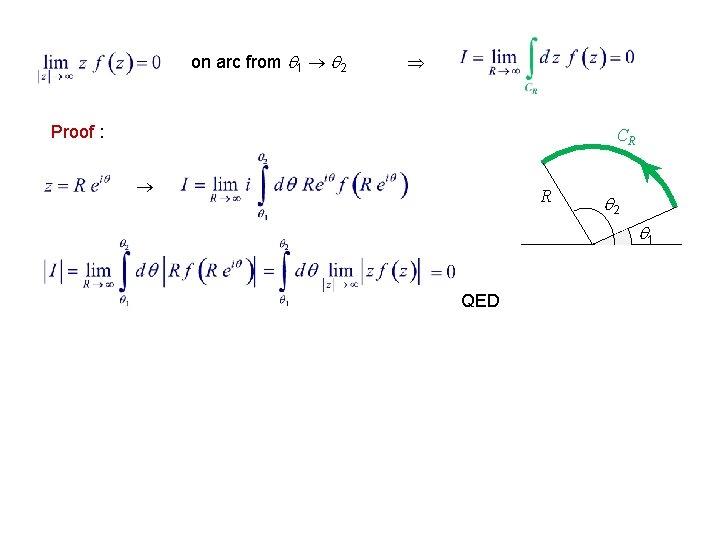
Integrals, Range ( , ) f is meromorphic in upper half z-plane, where C = Cx + CR R zj in upper plane Since (see next page for proof ) on upper plane zj in upper plane Obviously, one can also close the contour in the lower half plane.

on arc from 1 2 Proof : CR R 2 1 QED

Example 11. 8. 3. Integral of Meromorphic Function i Poles are at . Alternatively But only z+ is inside C. i

Integral with Complex Exponentials a > 0 & real. f analytic in upper plane, where In upper plane, y > 0 R Jordan’s lemma zj = poles of f in upper plane

Example 11. 8. 4. Oscillatory Integral Poles are at Only z+ is in upper plane with

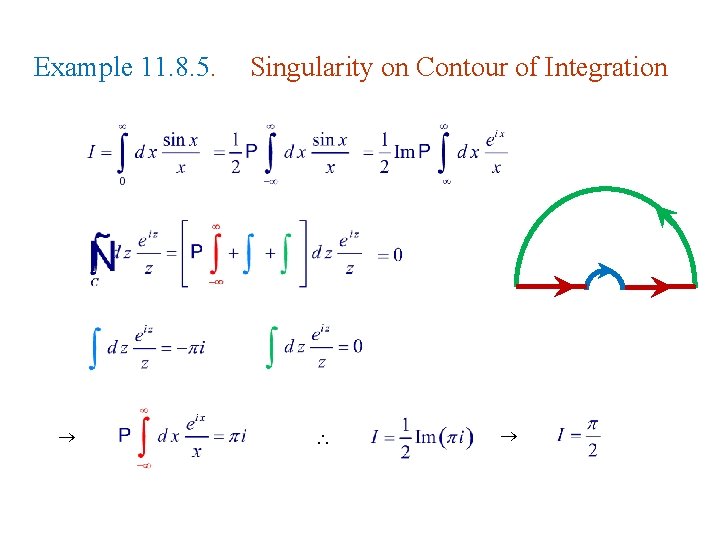
Example 11. 8. 5. Singularity on Contour of Integration

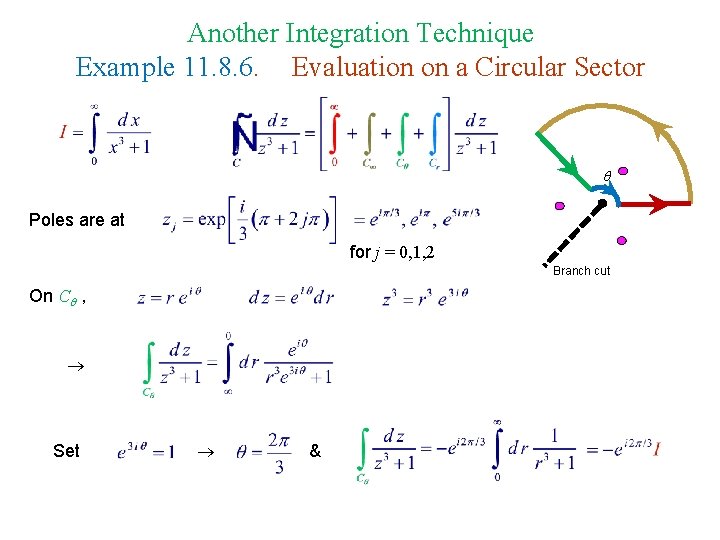
Another Integration Technique Example 11. 8. 6. Evaluation on a Circular Sector Poles are at for j = 0, 1, 2 Branch cut On C , Set &
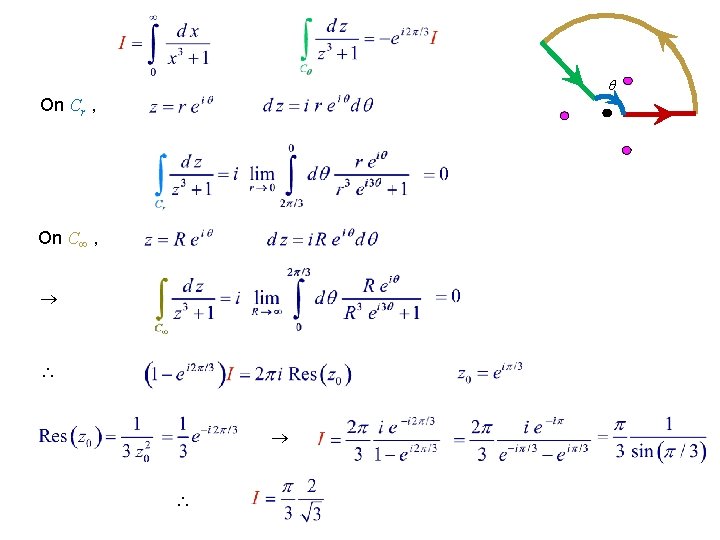
On Cr , On C ,

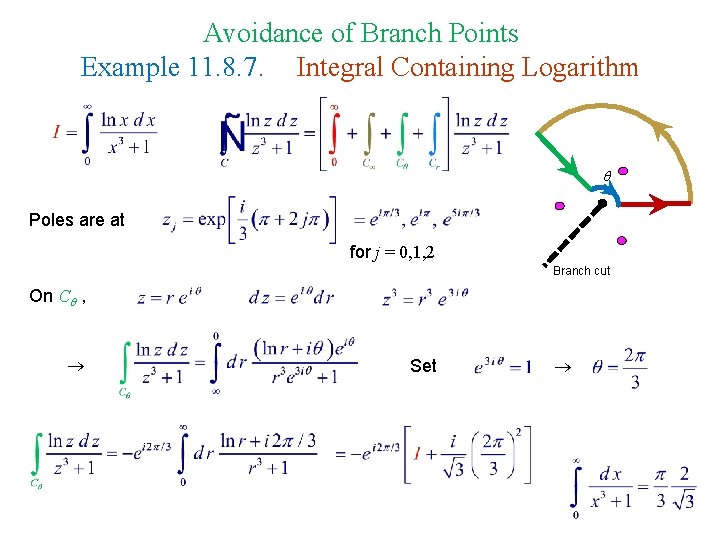
Avoidance of Branch Points Example 11. 8. 7. Integral Containing Logarithm Poles are at for j = 0, 1, 2 Branch cut On C , Set

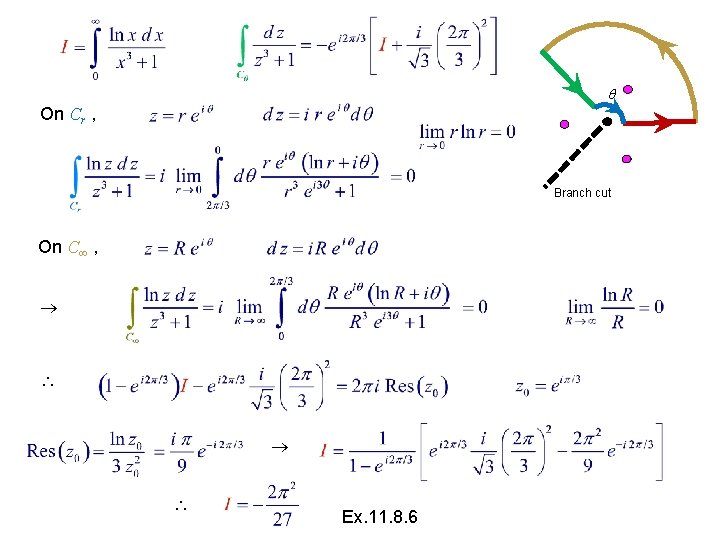
On Cr , Branch cut On C , Ex. 11. 8. 6

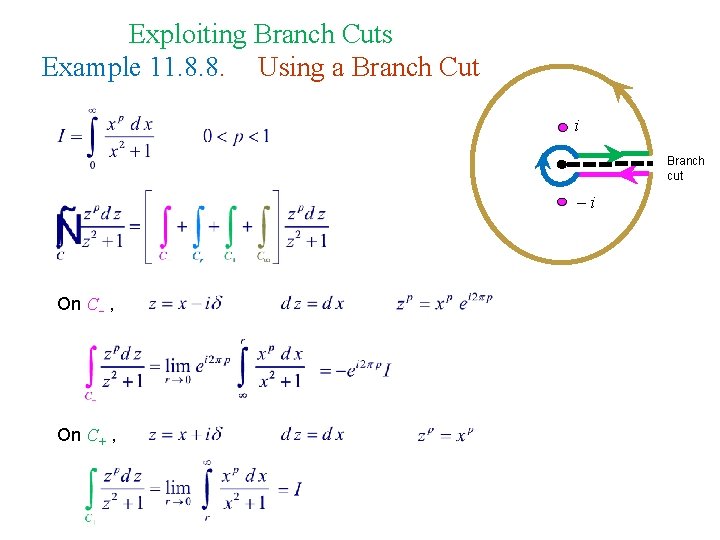
Exploiting Branch Cuts Example 11. 8. 8. Using a Branch Cut i Branch cut i On C , On C+ ,

i Branch cut i On Cr , On C ,

i Branch cut i Poles are at

Example 11. 8. 9. Ex. 11. 8. 6 -7 evaluated 1 st then use it to get , with a contour that avoids the branch cut. Here, we pretend to evaluate But ends up with Introducing a Branch Point using a branch cut. .

On C , On C+ ,

On Cr , On C ,

for j = 0, 1, 2 Poles are at

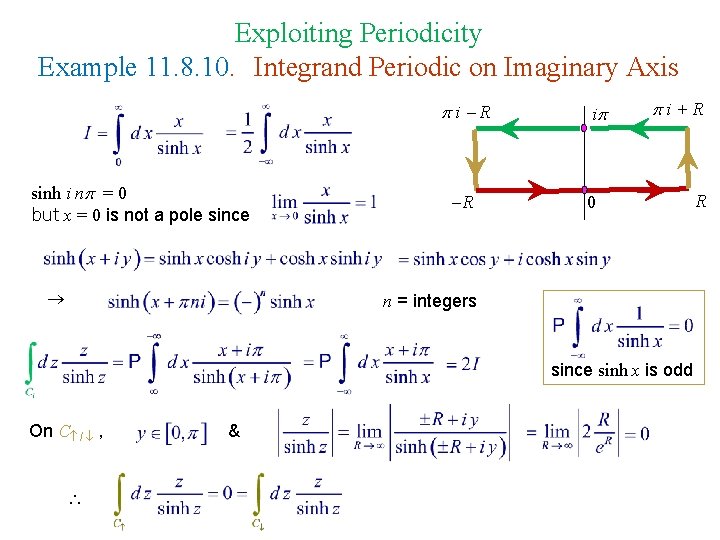
Exploiting Periodicity Example 11. 8. 10. Integrand Periodic on Imaginary Axis i R sinh i n = 0 but x = 0 is not a pole since R i i+R 0 n = integers since sinh x is odd On C / , & R

Pole on path counted as half.

9. Evaluation of Sums is meromorphic with simple poles at Consider where f is meromorphic with poles at zj. can be used to evaluate series.

Example 11. 9. 1. Evaluating a Sum a integer Poles of at with

Other Sum Formulae

Example 11. 9. 2. Another Sum has poles at z = 0, 1. has 2 nd order poles at z = 0, 1. Mathematica

10. Miscellaneous Topics Schwarz reflection principle : If f (z) is analytic over region R with R x-axis , and f (x) is real, then Proof : For any f (x) is real f (n) (x) is real.

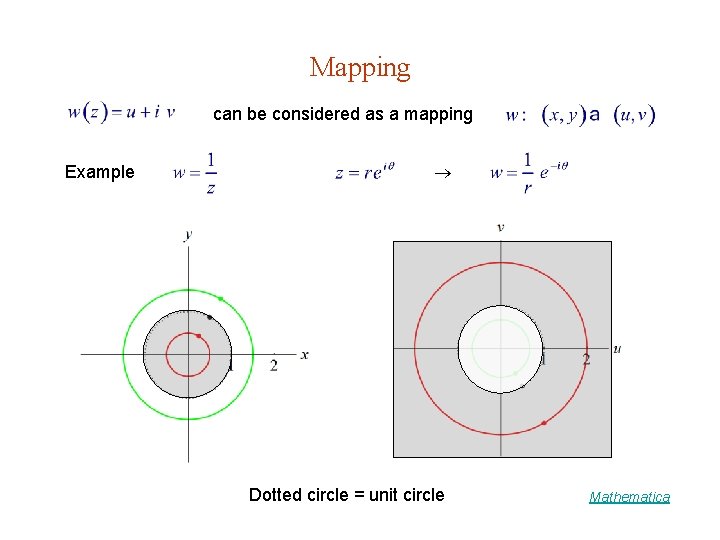
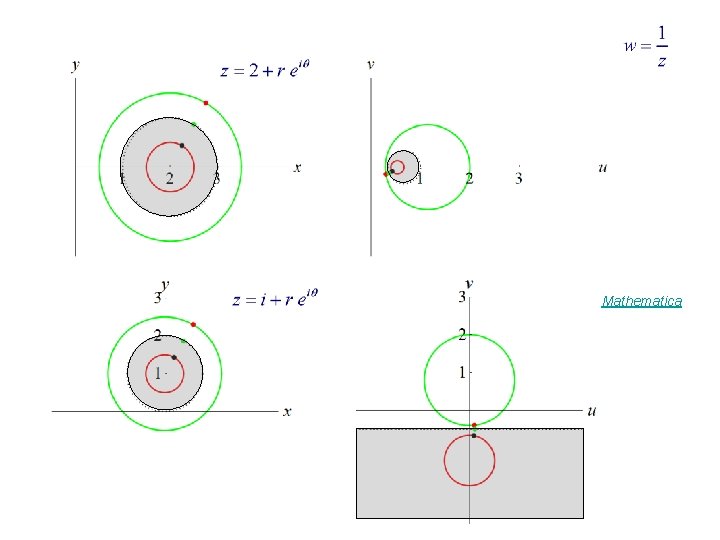
Mapping can be considered as a mapping Example Dotted circle = unit circle Mathematica

Mathematica
 Residue mathematica
Residue mathematica Residue theorem
Residue theorem Application of residue theorem to evaluate real integrals
Application of residue theorem to evaluate real integrals Application of residue theorem to evaluate real integrals
Application of residue theorem to evaluate real integrals Stoles theorem
Stoles theorem Interpersonal metafunction
Interpersonal metafunction Moral residue
Moral residue Complete residue system modulo 5
Complete residue system modulo 5 European pesticide residue workshop
European pesticide residue workshop Modal adjunct
Modal adjunct Ftoc2
Ftoc2 Fundamental theorem of vector calculus
Fundamental theorem of vector calculus Theorem 4 calculus
Theorem 4 calculus Fundamental theorem of calculus
Fundamental theorem of calculus Finding derivative with fundamental theorem of calculus
Finding derivative with fundamental theorem of calculus Calculus proof
Calculus proof Conjugate theorem
Conjugate theorem Remainder and factor theorem
Remainder and factor theorem What is rational root theorem
What is rational root theorem Remainder theorum
Remainder theorum Linear factors theorem and conjugate zeros theorem
Linear factors theorem and conjugate zeros theorem Factor theorem and remainder theorem
Factor theorem and remainder theorem Curve calculus
Curve calculus Mth 104
Mth 104 Calculus teeth
Calculus teeth What is calculus
What is calculus Liate calculus
Liate calculus Greg kelly calculus
Greg kelly calculus Hoffman calculus
Hoffman calculus Calculus 3
Calculus 3 Reciprocal rule differentiation
Reciprocal rule differentiation Jerome white ap calculus
Jerome white ap calculus What does calculus look like
What does calculus look like Black schoels
Black schoels Bernoulli differential equation examples
Bernoulli differential equation examples Mram calculus
Mram calculus Chapter p preparation for calculus
Chapter p preparation for calculus Calculus cookbook
Calculus cookbook Calculus equation example
Calculus equation example Half wave plate jones matrix
Half wave plate jones matrix Ap calculus ab jeopardy
Ap calculus ab jeopardy Elsa lambda calculus
Elsa lambda calculus Calculus adjective
Calculus adjective Stewart
Stewart Impact calculus
Impact calculus Teorema fundamental kalkulus 1
Teorema fundamental kalkulus 1 Multivariable calculus
Multivariable calculus