Chapter 7 Applications of Residues evaluation of definite






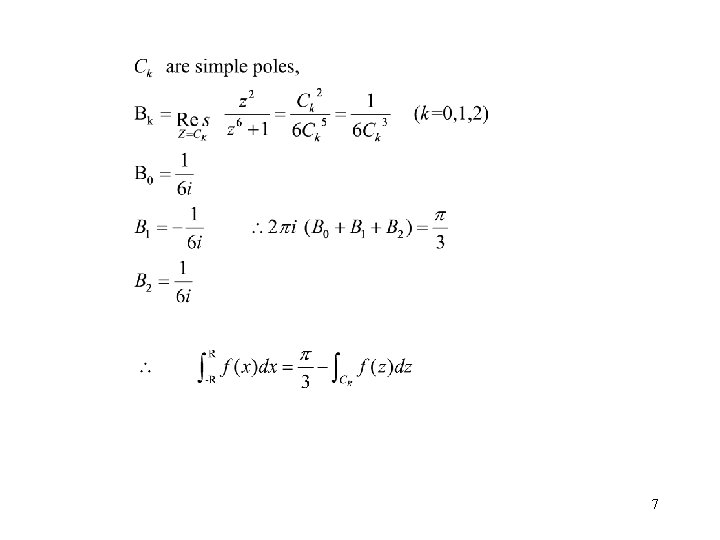
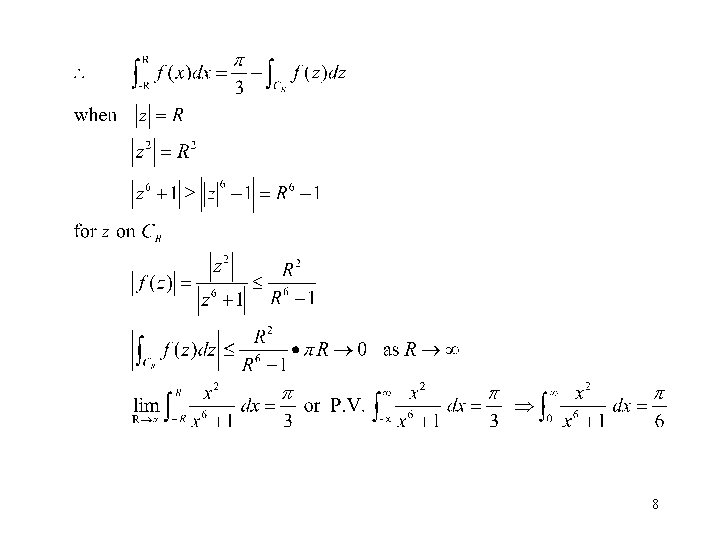










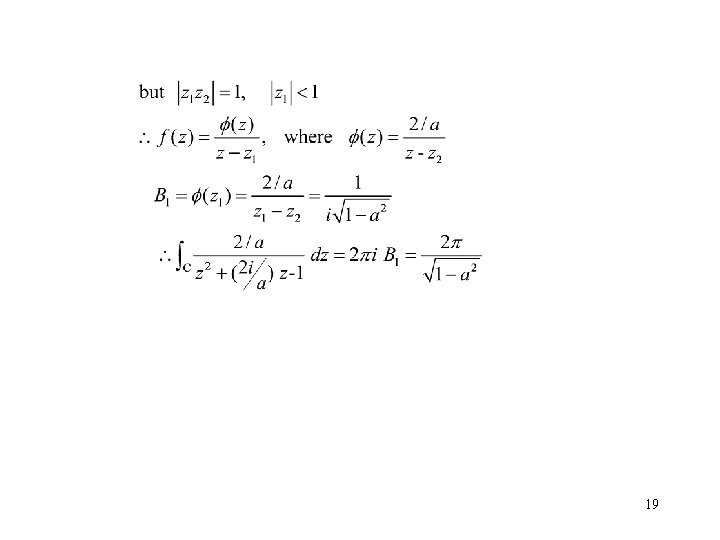












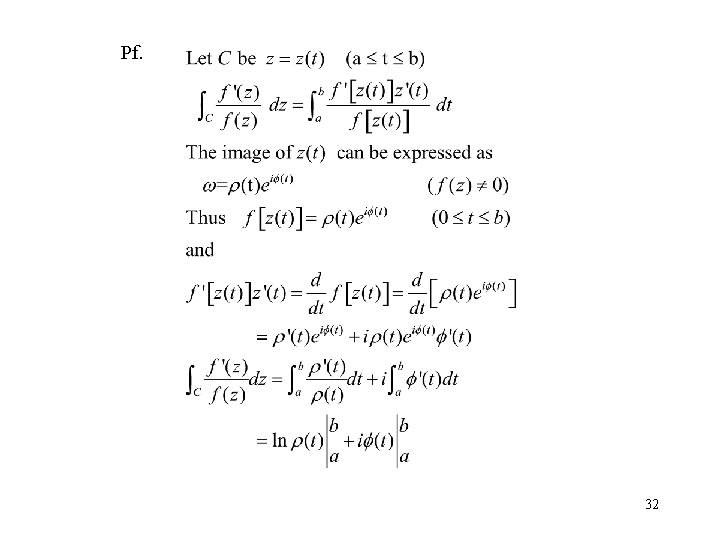













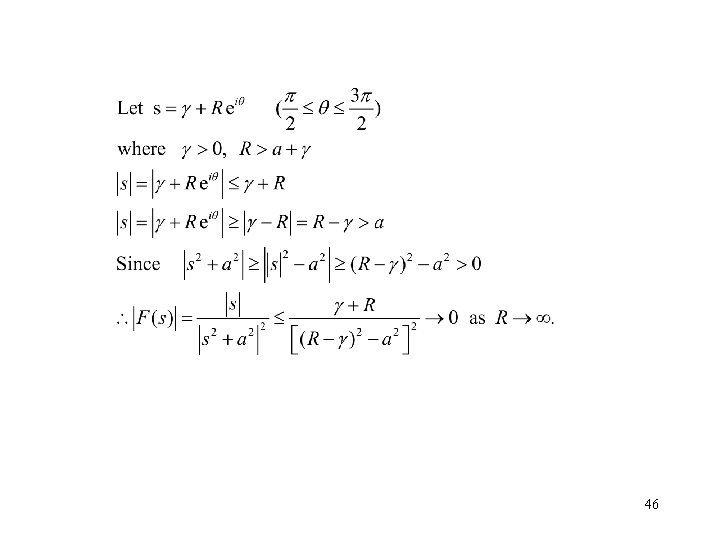
- Slides: 46

Chapter 7 Applications of Residues - evaluation of definite and improper integrals occurring in real analysis and applied math - finding inverse Laplace transform by the methods of summing residues. 60. Evaluation of Improper Integrals In calculus when the limit on the right exists, the improper integral is said to converge to that limit. 1

• If f(x) is continuous for all x, its improper integral over the is defined by When both of the limits here exist, integral (2) converges to their sum. • There is another value that is assigned to integral (2). i. e. , The Cauchy principal value (P. V. ) of integral (2). provided this single limit exists 2

If integral (2) converges its Cauchy principal value (3) exists. If is not, however, always true that integral (2) converges when its Cauchy P. V. exists. Example. (ex 8, sec. 60) 3

(1) (3) if exist 4

• To evaluate improper integral of p, q are polynomials with no factors in common. and q(x) has no real zeros. See example 5

Example has isolated singularities at 6 th roots of – 1. and is analytic everywhere else. Those roots are 6
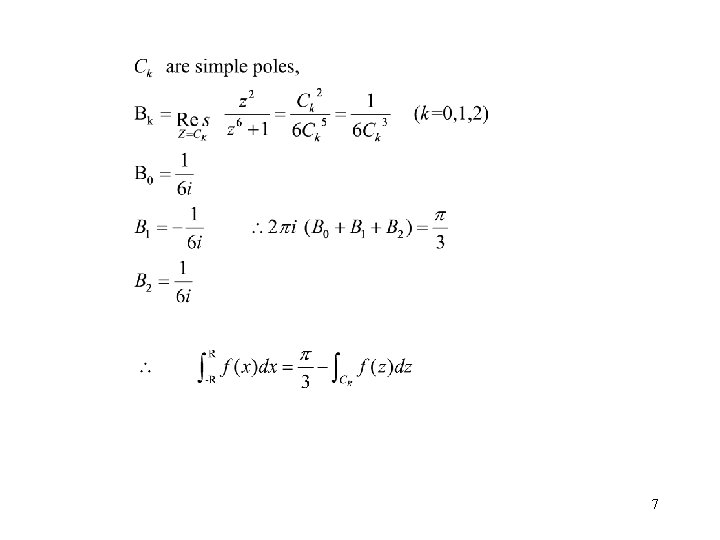
7
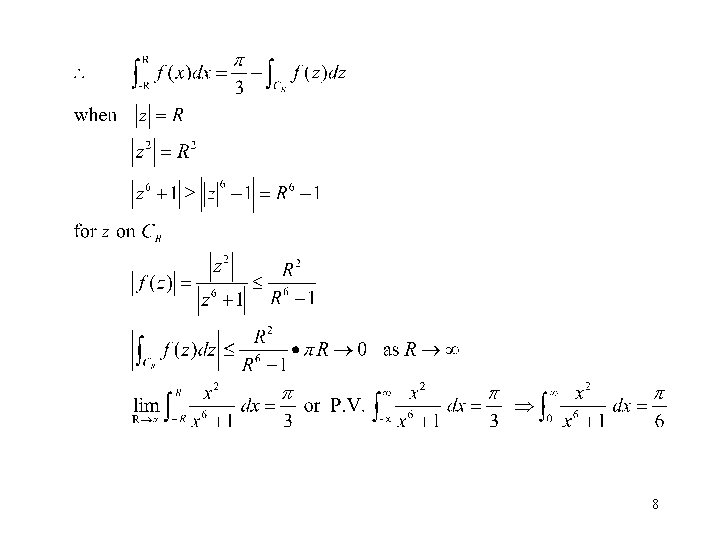
8

61. Improper Integrals Involving sines and cosines To evaluate Previous method does not apply since sinhay (See p. 70) However, we note that 9

Ex 1. An even function And note that is analytic everywhere on and above the real axis except at 10

Take real part 11

It is sometimes necessary to use a result based on Jordan’s inequality to evaluate 12

Suppose f is analytic at all points 13

Example 2. Sol: 14

15

But from Jordan’s Lemma 16

62. Definite Integrals Involving Sines and Cosines 17

18
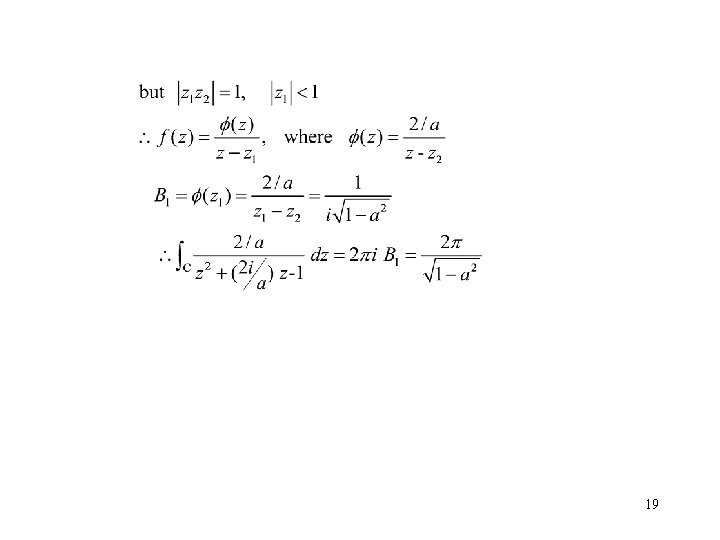
19

63. Indented Paths 20

21

Ex 1. Consider a simple closed contour 22

Jordan’s Lemma 23

64. Integrating Along a Branch Cut (P. 81, complex exponent) 24

25

Then 26

27

65. Argument Principle and Rouche’s Theorem A function f is said to be meromorphic in a domain D if it is analytic throughout D - except possibly for poles. Suppose f is meromorphic inside a positively oriented simple close contour C, and analytic and nonzero on C. The image of C under the transformation w = f(z), is a closed contour, not necessarily simple, in the w plane. 28

29

Positive: Negative: 30

The winding number can be determined from the number of zeros and poles of f interior to C. Number of poles zeros are finite (Ex 15, sec. 57) (Ex 4) Argument principle 31
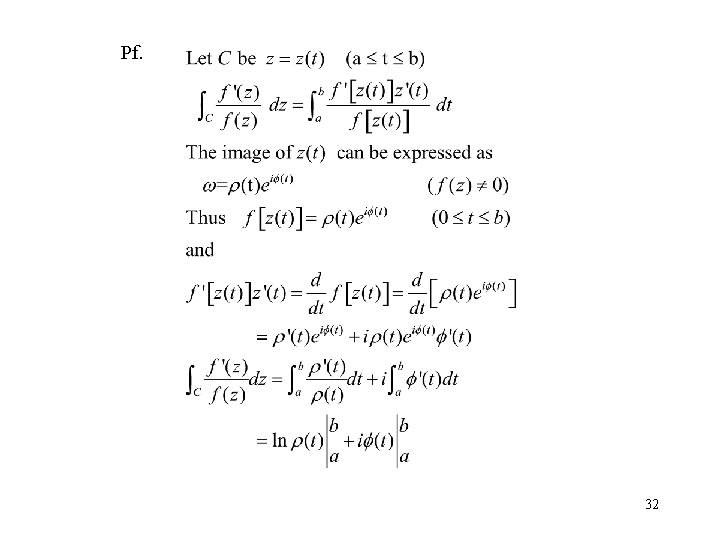
Pf. 32

33

34

35

Rouche’s theorem Thm 2. Pf. 36

37

38

66. Inverse Laplace Transforms Suppose that a function F of complex variable s is analytic throughout the finite s plane except for a finite number of isolated singularities. Bromwich integral 39

40

Jordan’s inequality 41

42

67. Example Exercise 12 When t is real 43

Ex 1. 44

45
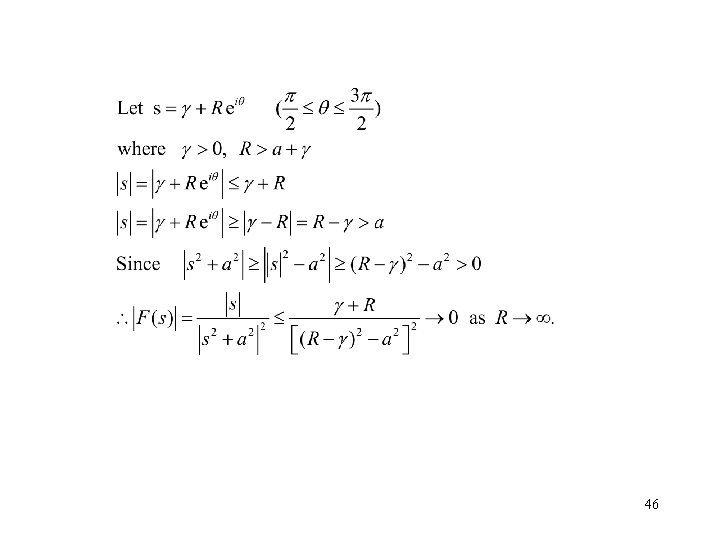
46
 Residue mathematica
Residue mathematica Application software and system software difference
Application software and system software difference Steering straight backward
Steering straight backward Chapter 28 unemployment problems and applications answers
Chapter 28 unemployment problems and applications answers Chapter 23:3 administering heat/cold applications
Chapter 23:3 administering heat/cold applications Chapter 8 linear programming applications solutions
Chapter 8 linear programming applications solutions Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Chapter 2 skills and applications
Chapter 2 skills and applications Line regulation
Line regulation Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Substitution rule
Substitution rule How to read summation notation
How to read summation notation A short rhyming poem with 14 lines.
A short rhyming poem with 14 lines. Kinetic theory of solids
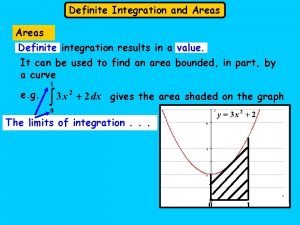
Kinetic theory of solids Indefinite integral and definite integral
Indefinite integral and definite integral La mochila plural
La mochila plural Is the composition uniform
Is the composition uniform Law of multiple composition
Law of multiple composition Definite composition example
Definite composition example Law of definite proportions examples
Law of definite proportions examples Definite vs indefinite
Definite vs indefinite Law of definite proportion
Law of definite proportion Spanish definite articles
Spanish definite articles Definite article for clase
Definite article for clase What is a definite article
What is a definite article Definite and indefinite articles spanish
Definite and indefinite articles spanish Unas clases singular
Unas clases singular Spanish indefinite articles
Spanish indefinite articles Unit factor method
Unit factor method Integration basic concepts
Integration basic concepts Arabic definite article
Arabic definite article Italian definite article chart
Italian definite article chart Italian definite article
Italian definite article Definite pronouns examples
Definite pronouns examples Riemann sum to integral
Riemann sum to integral Norm of a partition
Norm of a partition Rram formula
Rram formula What is ethics in philosophy
What is ethics in philosophy Definite knowledge
Definite knowledge Max min inequality definite integrals
Max min inequality definite integrals Definite loop python
Definite loop python Law of definite and multiple proportions worksheet answers
Law of definite and multiple proportions worksheet answers Https://www.choosemyplate.gov/resources/myplateplan
Https://www.choosemyplate.gov/resources/myplateplan Definite and indefinite articles in french
Definite and indefinite articles in french Cuadernos definite article
Cuadernos definite article Definite proportions example
Definite proportions example Definite loop
Definite loop