Definite Integration MATHEMATICS Definite CRASH Integration COURSE Definite

Definite Integration MATHEMATICS Definite CRASH Integration COURSE

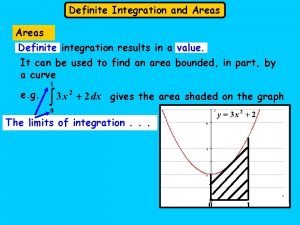
Definite Integration Fundamental Definition: A Let f(x) be a continuous function defined on [a, b], = F(x) + c. Then integral. = F(b) – F(a) is called definite

Definite Integration Note : 1. The indefinite integral , where as definite integral 2. Given we cannot find is a function of x ( Family of curves) is a number. we can find , but given

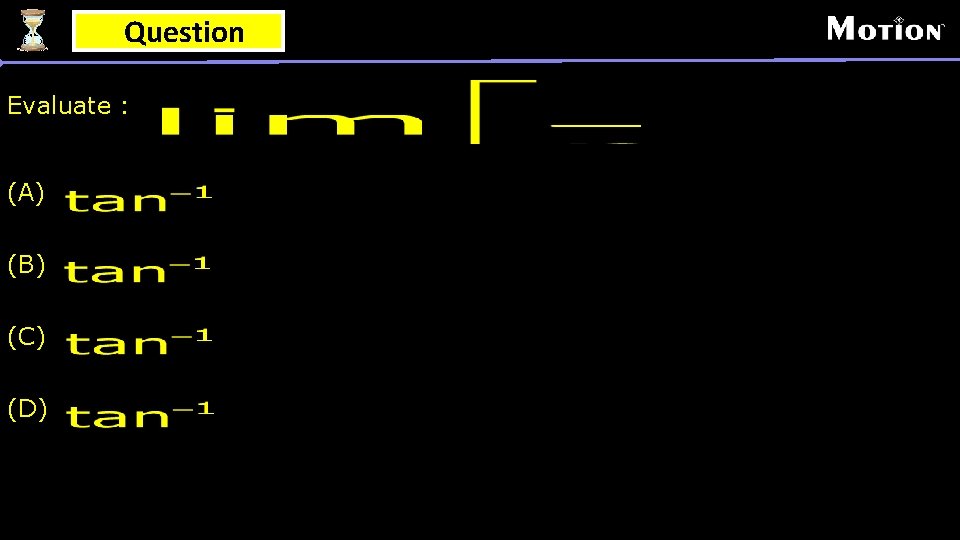
Question Evaluate : (A) (B) (C) (D)

Question The value of integral (A) (B) (C) (D) is :

Question

Question The integral (A) (B) (C) (D) dx is equal to :

Question A value of a such that (A) (B) -2 (C) 2 (D) is:

Question If (A) -1 (B) (C) (D) 1 , then m. n is equal to :

Question The integral (A) e(4 e– 1) (B) e(4 e+1) (C) 4 e 2– 1 (D) e(2 e– 1) equal :

Question If the value of the integral (A) (B) (C) (D) is , then k is equal to:

Definite Integration Properties of definite integral : P– 1 i. e. definite integral is independent of variable of integration. P– 2 P– 3 , where c may lie inside or outside the interval [a, b].

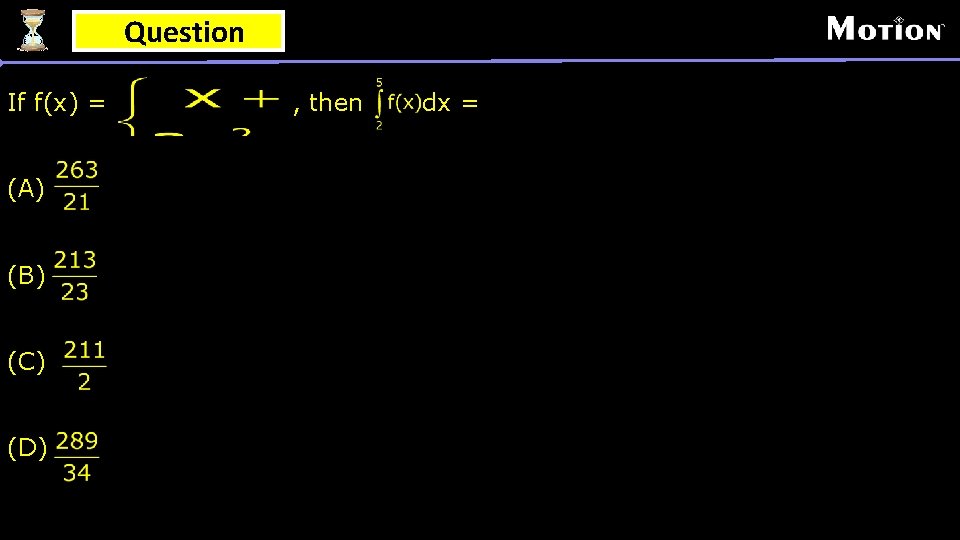
Question If f(x) = (A) (B) (C) (D) , then dx =

Question The integral (A) (B) (C) (D) is equal to :

Question Let [t] denote the greatest integer less than or equal to t. Then the value of is ____

Question

Question P – 4 (NENO Property) if f(–x) = f(x) i. e. f(x) is even =0 if f(–x) = –f (x) i. e. f(x) is odd

Question Evaluate : (A) (B) (C) (D)

Question

Question Evaluate : (A) 0 (B) 1 (C) 2 (D) 3

Question If and g(x) = logex, (x>0) then the value of the integral is : (A) loge 3 (B) loge 1 (C) loge 2 (D) logee

Question is equal to: (A) (B) (C) (D)

Definite Integration P – 5(King Property) Further

Question The value of (A) (B) (C) (D) is :

Question P – 6 ( Queen Property) If f(2 a – x) = f(x) =0 if f(2 a – x) = –f(x)

Question Evaluate : (A) 0 (B) 1 (C) 2 (D) 3

Question Evaluate : (A) (B) (C) (D)

Definite Integration Note :

Definite Integration P – 7 (Jack Property) If f(x) is a periodic function with period T, then (i) dx = n dx, n Î z (ii) n Î z, a Î R (iii) m, n Î z (iv) n Î z, a Î R (v) n Î z, a, b Î R

Question Evaluate : (A) 3(e - 1) (B) 3(e + 1) (C) 2(e – 1) (D) 2(e+1)

Question Evaluate : (A) 2 n +2 - sinv (B) 2 n – 2 - sinv (C) 2 n +2 + sinv (D) 2 n -2 + sinv and n Î z

Question

Definite Integration P – 8 If y(x) £ f (x) for a £ x £ b, then P – 9 Estimation of Definite Integration If m £ f(x) £ M for a £ x £ b, then m (b – a) £ Further if f(x) is monotonically decreasing in (a, b) then f(b)(b– a) < < f(a) (b – a) and if f(x) is monotonically increasing in (a, b) then f(a) (b – a) < < f(b) (b – a)

Definite Integration P - 10 : P – 11 : If f(x) ³ 0 on[a, b] then

Question

Definite Integration Leibnitz Theorem : If F(x) = , then = f(h(x)) h¢(x) – f(g(x)) g¢(x)

Question Evaluate : (A)is equal to 1 (B) is equal to 0 (C) does not exist (D) is equal to

Question If f(x) = (A) 1 (B) -1 (C) 2 (D) -2 , then find f¢(1)

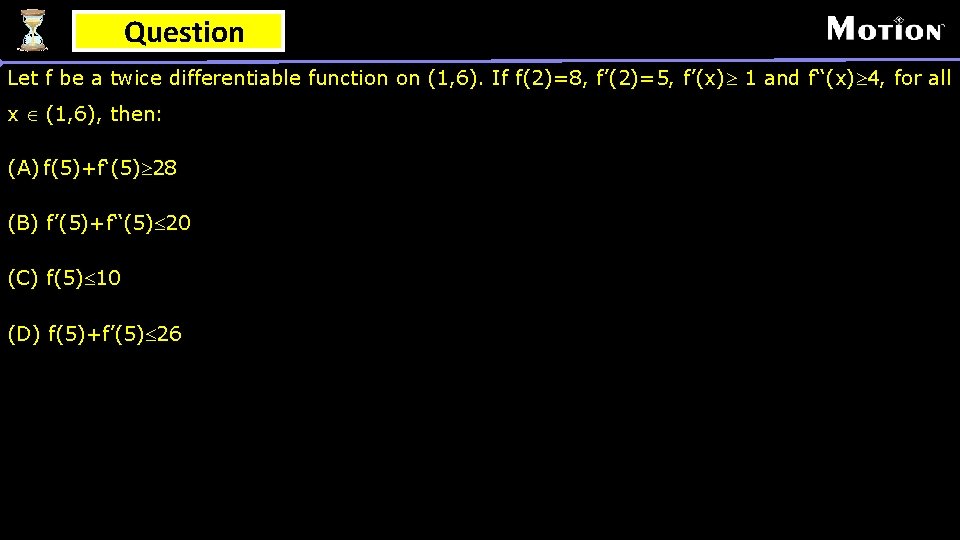
Question Let f be a twice differentiable function on (1, 6). If f(2)=8, f’(2)=5, f’(x)³ 1 and f‘‘(x)³ 4, for all x Î (1, 6), then: (A) f(5)+f‘(5)³ 28 (B) f’(5)+f‘‘(5)£ 20 (C) f(5)£ 10 (D) f(5)+f’(5)£ 26

Definite Integration Definite Integral as a Limit of Sum. Let f(x) be a continuous real valued function defined on the closed interval [a, b] which is divided into n parts as shown in figure. The point of division on x-axis are a, a + h, a + 2 h. . a + (n – 1)h, a + nh, where = h.

Definite Integration Let Sn denotes the area of these n rectangles. Then, Sn = hf(a) + hf(a + h) + hf(a + 2 h) +. . . . +hf(a + (n – 1)h) Clearly, Sn is area very close to the area of the region bounded by curve y = f(x), x–axis and the ordinates x = a, x = b. Hence Sn

Definite Integration Note : 1. We can also write Sn = hf(a + h) + hf(a + 2 h) +. . + hf(a + nh) and 2. If a = 0, b = 1,

Question Evaluate : (A) (B) (C) (D)

Question

Question Evaluate : (A) 1/e (B) 2/e (C) 3/e (D) 4/e

Question Reduction Formulae in Definite Integrals If I 1 = a equals to : (A) (B) (C) (D) dx and I 2 = dx such that I 2 = a. I 1 then

Question

Question Walli’s Formula : Im, n =

Question Evaluate : (A) (B) (C) (D)

Question Evaluate : (A) (B) (C) (D)