The Definite Integral When we find the area
















![Definite Integral of a continuous function on [a, b] Let f be continuous on Definite Integral of a continuous function on [a, b] Let f be continuous on](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-24.jpg)
















![Rules for Definite Integrals 7) Domination: f(x) ≥ g(x) on [a, b] f(x) ≥ Rules for Definite Integrals 7) Domination: f(x) ≥ g(x) on [a, b] f(x) ≥](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-43.jpg)

















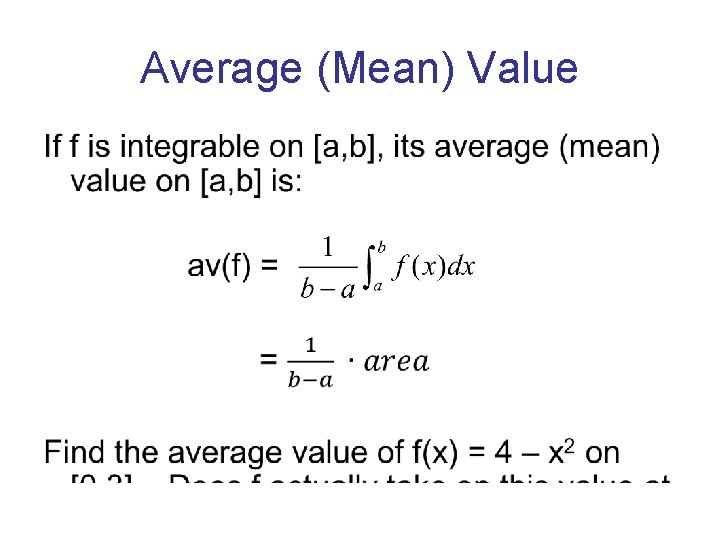

![Mean Value Theorem for Definite Integrals If f is continuous on [a, b], then Mean Value Theorem for Definite Integrals If f is continuous on [a, b], then](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-63.jpg)



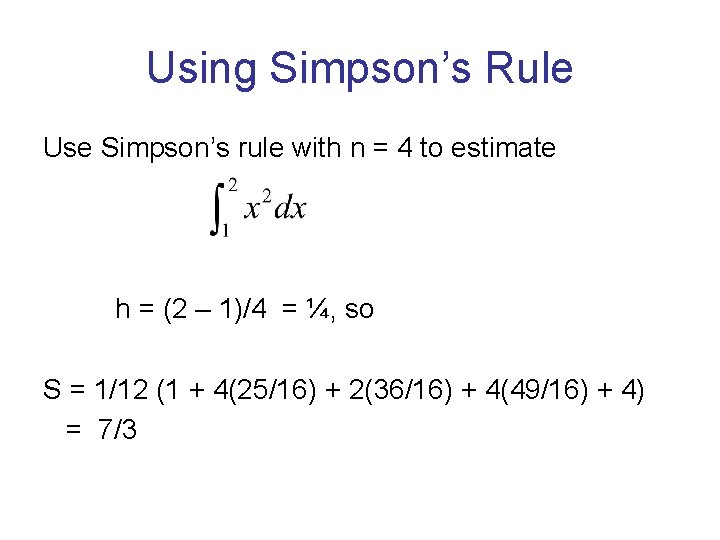
- Slides: 67

The Definite Integral

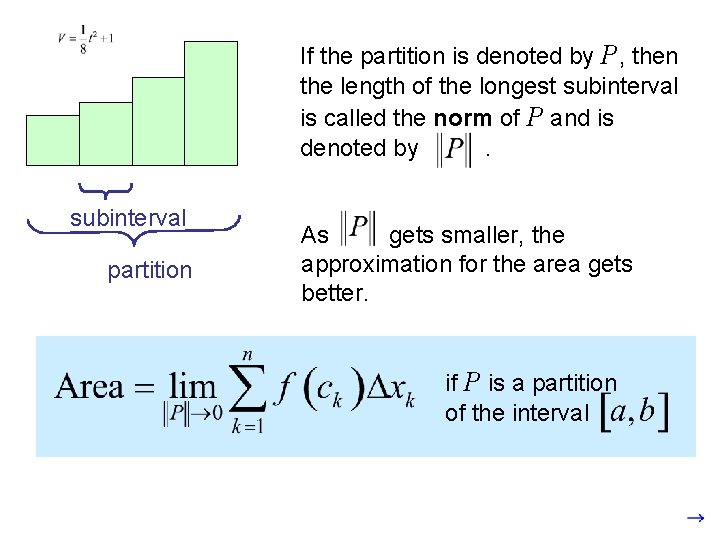
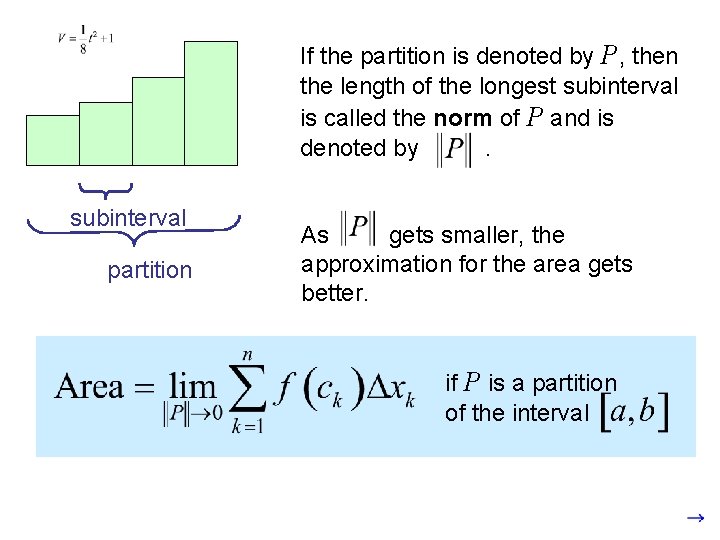
When we find the area under a curve by adding rectangles, the answer is called a Rieman sum. The width of a rectangle is called a subinterval The entire interval is called the partition Subintervals do not all have to be the same size.

If the partition is denoted by P, then the length of the longest subinterval is called the norm of P and is denoted by . subinterval partition As gets smaller, the approximation for the area gets better. if P is a partition of the interval

is called the definite integral of over . If we use subintervals of equal length, then the length of a subinterval is: The definite integral is then given by:

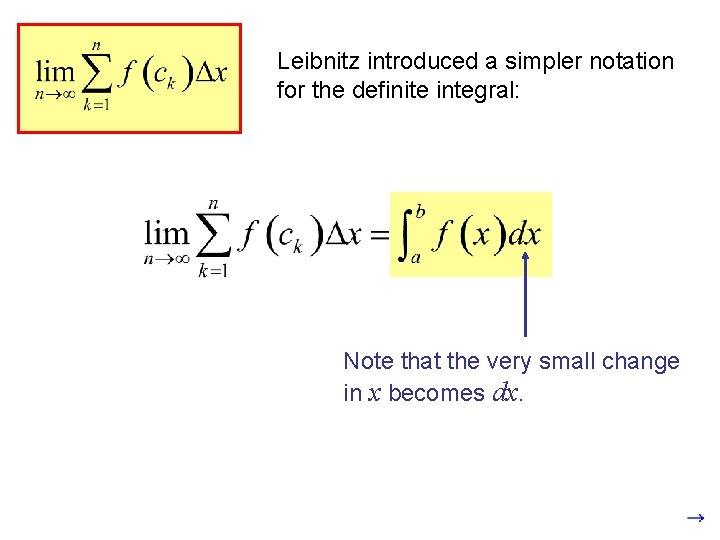
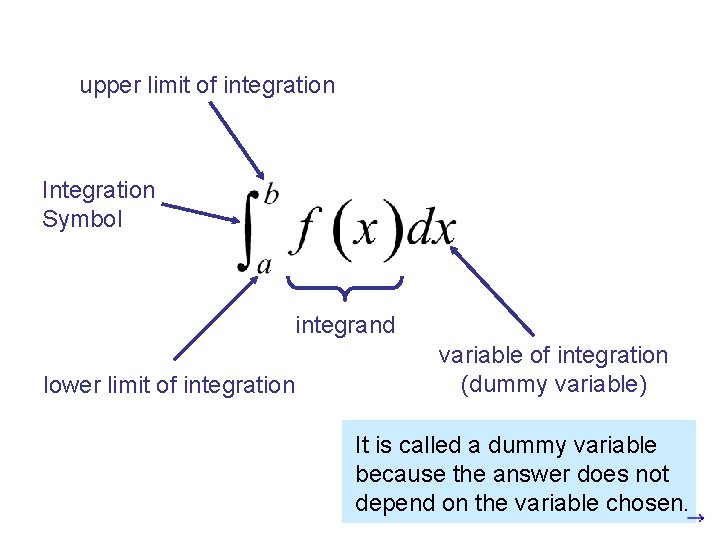
Leibnitz introduced a simpler notation for the definite integral: Note that the very small change in x becomes dx.

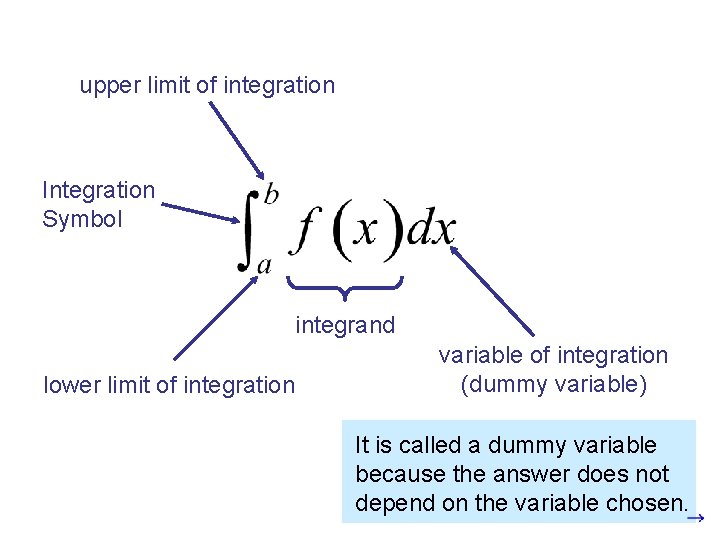
upper limit of integration Integration Symbol integrand lower limit of integration variable of integration (dummy variable) It is called a dummy variable because the answer does not depend on the variable chosen.

We have the notation for integration, but we still need to learn how to evaluate the integral.

In section 6. 1, we considered an object moving at a constant rate of 3 ft/sec. Since rate. time = distance: If we draw a graph of the velocity, the distance that the object travels is equal to the area under the line. After 4 seconds, the object has gone 12 feet. velocity time

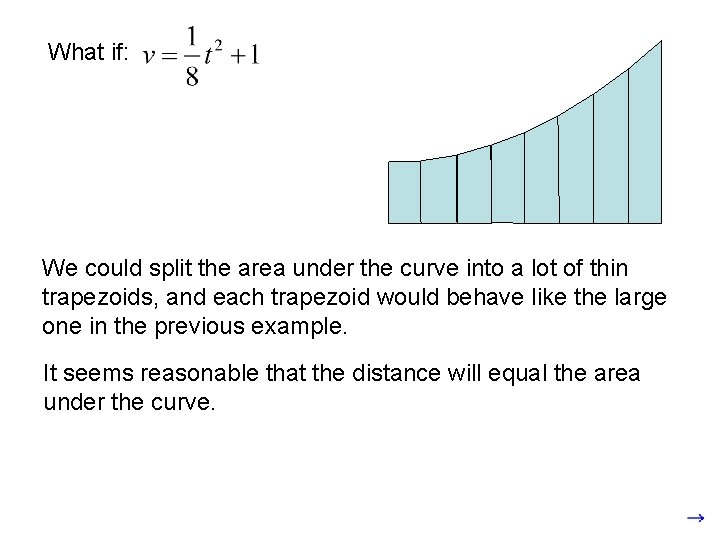
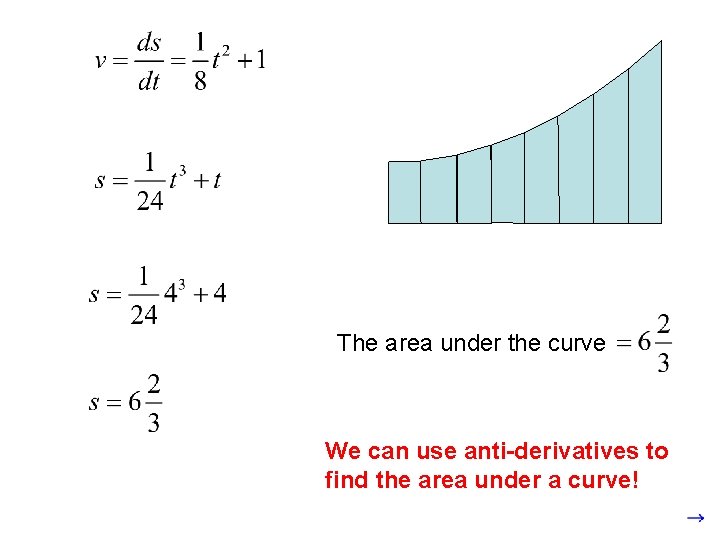
If the velocity varies: Distance: (C=0 since s=0 at t=0) After 4 seconds: The distance is still equal to the area under the curve! Notice that the area is a trapezoid.

What if: We could split the area under the curve into a lot of thin trapezoids, and each trapezoid would behave like the large one in the previous example. It seems reasonable that the distance will equal the area under the curve.

The area under the curve We can use anti-derivatives to find the area under a curve!

Riemann Sums • Sigma notation enables us to express a large sum in compact form

Calculus Date: 2/18/2014 ID Check Objective: SWBAT apply properties of the definite integral Do Now: Set up two related rates problems from the HW Worksheet 6, 10 Turn UP! MAP HW Requests: pg 276 #23, 25, 26, Turn in #28 E. C In class: Finish Sigma notation Maximize Academic Continue Definite Integrals Potential HW: pg 286 #1, 3, 5, 9, 13, 15, 17, 19, 21, Announcements: “There is something in every one of you that waits and listens for the sound of the genuine in yourself. It is the only true guide you will ever have. And if you cannot hear it, you will all of your life spend your days on the ends of strings that somebody else pulls. ” ― Howard Thurman

When we find the area under a curve by adding rectangles, the answer is called a Rieman sum. The width of a rectangle is called a subinterval The entire interval is called the partition Subintervals do not all have to be the same size.

The width of a rectangle is called a subinterval. The entire interval is called the partition. subinterval Let’s divide partition into 8 subintervals. partition Pg 274 #9 Write this as a Riemann sum. 6 subintervals

If the partition is denoted by P, then the length of the longest subinterval is called the norm of P and is denoted by . subinterval partition As gets smaller, the approximation for the area gets better. if P is a partition of the interval

is called the definite integral of over . If we use subintervals of equal length, then the length of a subinterval is: The definite integral is then given by:

Leibnitz introduced a simpler notation for the definite integral: Note that the very small change in x becomes dx. Note as n gets larger and larger the definite integral approaches the actual value of the area.

upper limit of integration Integration Symbol integrand lower limit of integration variable of integration (dummy variable) It is called a dummy variable because the answer does not depend on the variable chosen.

Calculus Date: 2/19/2014 ID Check Objective: SWBAT apply properties of the definite integral Do Now: Bell Ringer Quiz HW Requests: pg 276 #25, 26, pg 286 1 -15 odds Turn UP! MAP In class: pg 276 #23, 28 Continue Definite Integrals HW: pg 286 #17 -35 odds Maximize Academic Announcements: Potential “There is something in every one of you that waits and listens for the sound of the genuine in yourself. It is the only true guide you will ever have. And if you cannot hear it, you will all of your life spend your days on the ends of strings that somebody else pulls. ” ― Howard Thurman

Bell Ringer Quiz (10 minutes) •

Riemann Sums • LRAM, MRAM, and RRAM are examples of Riemann sums • Sn = This sum, which depends on the partition P and the choice of the numbers ck, is a Riemann sum for f on the interval [a, b]

Definite Integral as a Limit of Riemann Sums Let f be a function defined on a closed interval [a, b]. For any partition P of [a, b], let the numbers ck be chosen arbitrarily in the subintervals [xk-1, xk]. If there exists a number I such that no matter how P and the ck’s are chosen, then f is integrable on [a, b] and I is the definite integral of f over [a, b].
![Definite Integral of a continuous function on a b Let f be continuous on Definite Integral of a continuous function on [a, b] Let f be continuous on](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-24.jpg)
Definite Integral of a continuous function on [a, b] Let f be continuous on [a, b], and let [a, b] be partitioned into n subintervals of equal length Δx = (b-a)/n. Then the definite integral of f over [a, b] is given by where each ck is chosen arbitrarily in the kth subinterval.

Definite integral This is read as “the integral from a to b of f of x dee x” or sometimes as “the integral from a to b of f of x with respect to x. ”

Using Definite integral notation The function being integrated is f(x) = 3 x 2 – 2 x + 5 over the interval [-1, 3]

Definition: Area under a curve If y = f(x) is nonnegative and integrable over a closed interval [a, b], then the area under the curve of y = f(x) from a to b is the integral of f from a to b, We can use integrals to calculate areas and we can use areas to calculate integrals.

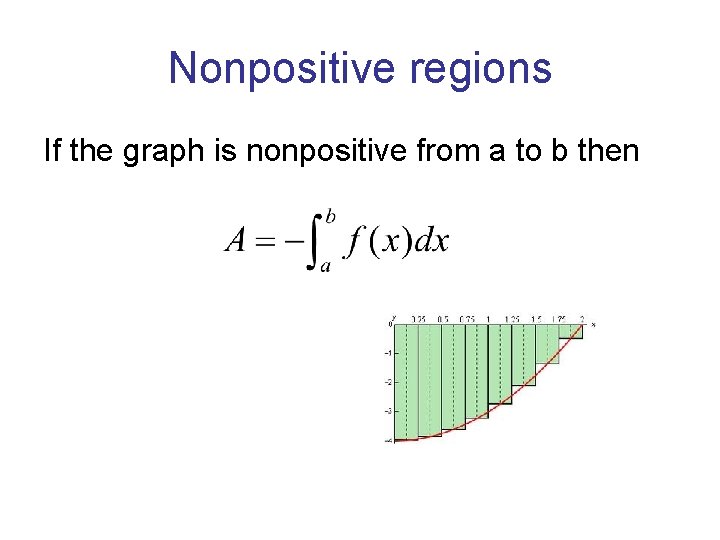
Nonpositive regions If the graph is nonpositive from a to b then

Area of any integrable function = (area above the x-axis) – (area below x-axis)

Turn UP! MAP Maximize Academic Potential

Integral of a Constant If f(x) = c, where c is a constant, on the interval [a, b], then

Evaluating Integrals using areas We can use integrals to calculate areas and we can use areas to calculate integrals. Using areas, evaluate the integrals: 1) 2)

Evaluating Integrals using areas Evaluate using areas: 3) 4) (a<b)

Evaluating integrals using areas Evaluate the discontinuous function: Since the function is discontinuous at x = 0, we must divide the areas into two pieces and find the sum of the areas = -1 + 2 = 1

Integrals on a Calculator You can evaluate integrals numerically using the calculator. The book denotes this by using NINT. The calculator function fn. Int is what you will use. = fn. Int(xsinx, x, -1, 2) is approx. 2. 04

Evaluate Integrals on calculator • Evaluate the following integrals numerically: 1) = approx. 3. 14 2) = approx. . 89

Rules for Definite Integrals 1) Order of Integration:

Rules for Definite Integrals 2) Zero:

Rules for Definite Integrals 3) Constant Multiple: Any number k k= -1

Rules for Definite Integrals 4) Sum and Difference:

Rules for Definite Integrals 5) Additivity:

Rules for Definite Integrals 6) Max-Min Inequality: If max f and min f are the maximum and minimum values of f on [a, b] then: min f ∙ (b – a) ≤ ≤ max f ∙ (b – a)
![Rules for Definite Integrals 7 Domination fx gx on a b fx Rules for Definite Integrals 7) Domination: f(x) ≥ g(x) on [a, b] f(x) ≥](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-43.jpg)
Rules for Definite Integrals 7) Domination: f(x) ≥ g(x) on [a, b] f(x) ≥ 0 on [a, b] ≥ 0 (g =0)

Using the rules for integration Suppose: Find each of the following integrals, if possible: a) b) d) c) e) f)

Calculus Date: 2/27/2014 ID Check Obj: SWBAT connect Differential and Integral Calculus Do Now: http: //www. youtube. com/watch? v=mm. Mie. Ll-Jzs HW Requests: 145 #2 -34 evens and 33 HW: Complete SM pg 156, pg 306 #1 -19 odds Announcements: Mid Chapter Test Fri. Sect. 6. 1 -6. 3 Maximize Academic Careful of units, meaning of area, Potential asymptotes, properties of integrals Handout Inverses Saturday Tutoring 10 -1 (limits) “There is something in every one of you that waits and listens for the sound of the genuine in yourself. It is the only true guide you will ever have. And if you cannot hear it, you will all of your life spend your days on the ends of strings that somebody else pulls. ” Turn UP! MAP

The Fundamental Theorem of Calculus, Part I • Antiderivative Derivative

Applications of The Fundamental Theorem of Calculus, Part I 1. 2.

Applications of The Fundamental Theorem of Calculus, Part I •

Applications of The Fundamental Theorem of Calculus, Part I •

Applications of The Fundamental Theorem of Calculus, Part I Find dy/dx. y = Since this has an x on both ends of the integral, it must be separated.

Applications of The Fundamental Theorem of Calculus, Part I =

Applications of The Fundamental Theorem of Calculus, Part I = =

The Fundamental Theorem of Calculus, Part 2 If f is continuous at every point of [a, b], and if F is any antiderivative of f on [a, b], then This part of the Fundamental Theorem is also called the Integral Evaluation Theorem.

Applications of The Fundamental Theorem of Calculus, Part 2 •

End here

Calculus Date: 2/27/2014 ID Check Obj: SWBAT connect Differential and Integral Calculus Do Now: http: //www. youtube. com/watch? v=mm. Mie. Ll-Jzs HW Requests: 145 #2 -34 evens and 33 HW: SM pg 156 Announcements: Mid Chapter Test Fri. Sect. 6. 1 -6. 3 Maximize Academic Careful of units, meaning of area, Potential asymptotes, properties of integrals Handout Inverses Saturday Tutoring 10 -1 (limits) “There is something in every one of you that waits and listens for the sound of the genuine in yourself. It is the only true guide you will ever have. And if you cannot hear it, you will all of your life spend your days on the ends of strings that somebody else pulls. ” Turn UP! MAP

The Fundamental Theorem of Calculus, Part I • Antiderivative Derivative

The Fundamental Theorem of Calculus, Part 2 If f is continuous at every point of [a, b], and if F is any antiderivative of f on [a, b], then This part of the Fundamental Theorem is also called the Integral Evaluation Theorem.

Antidifferentiation A function F(x) is an antiderivative of a function f(x) if F’(x) = f(x) for all x in the domain of f. The process of finding an antiderivative is called antidifferentiation. If F is any antiderivative of f then = F(x) + C If x = a, then 0 = F(a) + C C = -F(a) = F(x) – F(a)

Using the rules for definite integrals Show that the value of is less than 3/2 The Max-Min Inequality rule says the max f. (b – a) is an upper bound. The maximum value of √(1+cosx) on [0, 1] is √ 2 so the upper bound is: √ 2(1 – 0) = √ 2 , which is less than 3/2
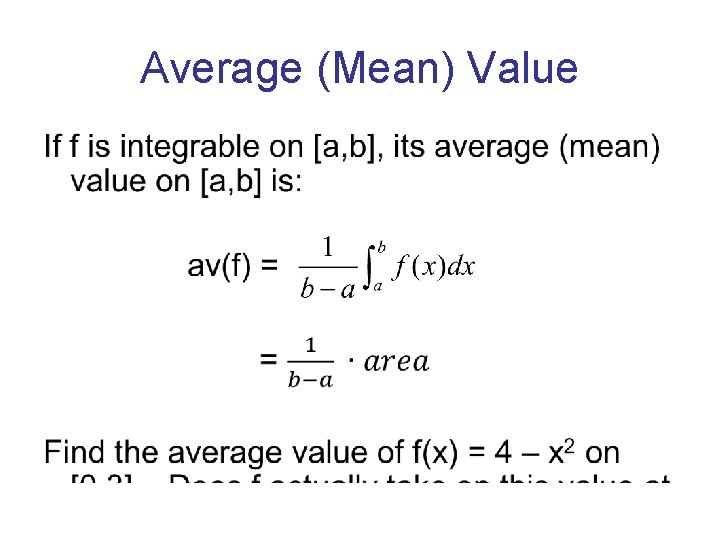
Average (Mean) Value •

Applying the Mean Value Av(f) = = 1/3(3) = 1 Use fn. Int 4 – x 2 = 1 when x = ± √ 3 but only √ 3 falls in the interval from [0, 3], so x = √ 3 is the place where the function assumes the average.
![Mean Value Theorem for Definite Integrals If f is continuous on a b then Mean Value Theorem for Definite Integrals If f is continuous on [a, b], then](https://slidetodoc.com/presentation_image/325dd6b17f2bdbc27542df56b9913643/image-63.jpg)
Mean Value Theorem for Definite Integrals If f is continuous on [a, b], then at some point c in [a, b],

Trapezoidal Rule To approximate , use T = (y 0 + 2 y 1 + 2 y 2 + …. 2 yn-1 + yn) where [a, b] is partitioned into n subintervals of equal length h = (b-a)/n.

Using the trapezoidal rule Use the trapezoidal rule with n = 4 to estimate h = (2 -1)/4 or ¼, so T = 1/8( 1+2(25/16)+2(36/16)+2(49/16)+4) = 75/32 or about 2. 344

Simpson’ Rule To approximate , use S = (y 0 + 4 y 1 + 2 y 2 + 4 y 3…. 2 yn-2 +4 yn-1 + yn) where [a, b] is partitioned into an even number n subintervals of equal length h =(b –a)/n.
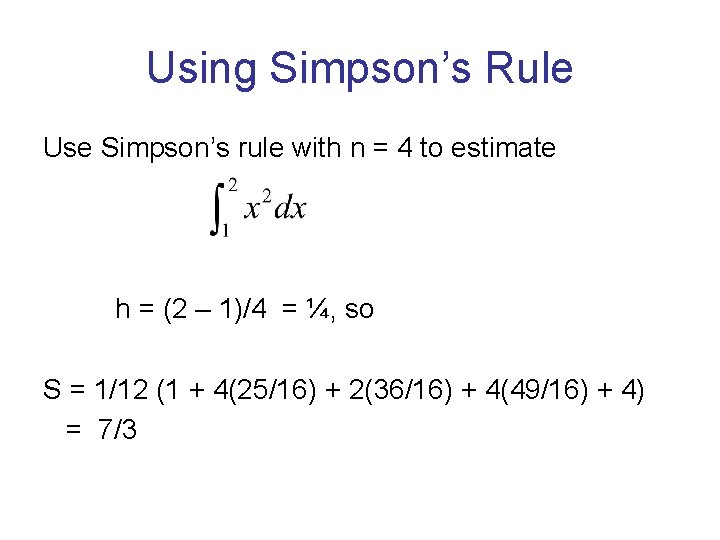
Using Simpson’s Rule Use Simpson’s rule with n = 4 to estimate h = (2 – 1)/4 = ¼, so S = 1/12 (1 + 4(25/16) + 2(36/16) + 4(49/16) + 4) = 7/3
 Indefinite integral
Indefinite integral Example of definite integral
Example of definite integral Riemann sum to integral
Riemann sum to integral Example of definite integral
Example of definite integral Definite integral denotes
Definite integral denotes Integral to sigma notation
Integral to sigma notation Definite integral integration by parts
Definite integral integration by parts Site:slidetodoc.com
Site:slidetodoc.com Integral citation example
Integral citation example Integral and non integral citation
Integral and non integral citation Integral permukaan adalah
Integral permukaan adalah Integral and non integral foreign operations
Integral and non integral foreign operations Integral udv = uv - integral vdu
Integral udv = uv - integral vdu Lateral edge
Lateral edge How to find the general indefinite integral
How to find the general indefinite integral Integration area under curve
Integration area under curve Find the volume of the composite figure
Find the volume of the composite figure How to find area of a sector with radians
How to find area of a sector with radians Area of a sector in radians
Area of a sector in radians How to find the surface area of a right triangular prism
How to find the surface area of a right triangular prism Surface area equation for rectangular prism
Surface area equation for rectangular prism Surface area of a triangular pyramid formula
Surface area of a triangular pyramid formula Hexagonal prism surface area calculator
Hexagonal prism surface area calculator Lateral surface area formula triangular prism
Lateral surface area formula triangular prism How to calculate population density
How to calculate population density Perimeter and area of composite figures
Perimeter and area of composite figures Triangular prism net
Triangular prism net X +4
X +4 Arc lengths and areas of sectors
Arc lengths and areas of sectors Find the area of the isosceles trapezoid.
Find the area of the isosceles trapezoid. Rectangle area formula
Rectangle area formula What is the area of this circle
What is the area of this circle Surface areas of prisms and cylinders
Surface areas of prisms and cylinders Rectangular prism net
Rectangular prism net Area of irregular shape
Area of irregular shape Cuboid perimeter and area
Cuboid perimeter and area Find the area of each shape
Find the area of each shape How to calculate area of shapes
How to calculate area of shapes How to find surface area of pentagonal prism
How to find surface area of pentagonal prism Find the surface area of the composite solid
Find the surface area of the composite solid Area of a regular polygon
Area of a regular polygon Area of each sector
Area of each sector How to get the area of a circle with the circumference
How to get the area of a circle with the circumference How to find the area diameter of a circle
How to find the area diameter of a circle Perimeter of a sector
Perimeter of a sector 11-2 surface areas of prisms and cylinders answers
11-2 surface areas of prisms and cylinders answers Area between curves formula
Area between curves formula Mathswatch
Mathswatch Area of oblique cone
Area of oblique cone How to calculate area of shape
How to calculate area of shape Find the area of shaded portion of the given figure.
Find the area of shaded portion of the given figure. How to find surface area of composite figures
How to find surface area of composite figures 7-1 find areas of parallelograms and rhombuses
7-1 find areas of parallelograms and rhombuses Find the lateral area of the regular pyramid. la= sq. units
Find the lateral area of the regular pyramid. la= sq. units Find the area of each figure
Find the area of each figure Determine the volume of the composite figure
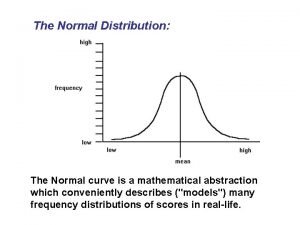
Determine the volume of the composite figure How to get the area of a normal curve
How to get the area of a normal curve Find the area
Find the area Area of circle diameter
Area of circle diameter Find the perimeter
Find the perimeter What shape is this
What shape is this Lateral
Lateral Area reference example
Area reference example Find the surface area of the regular pyramid.
Find the surface area of the regular pyramid. How to find sector area
How to find sector area Find the area of the figure below
Find the area of the figure below Find the area of each figure
Find the area of each figure Cobol area a and area b
Cobol area a and area b