MTH 104 Lecture 9 Calculus and Analytical Geometry







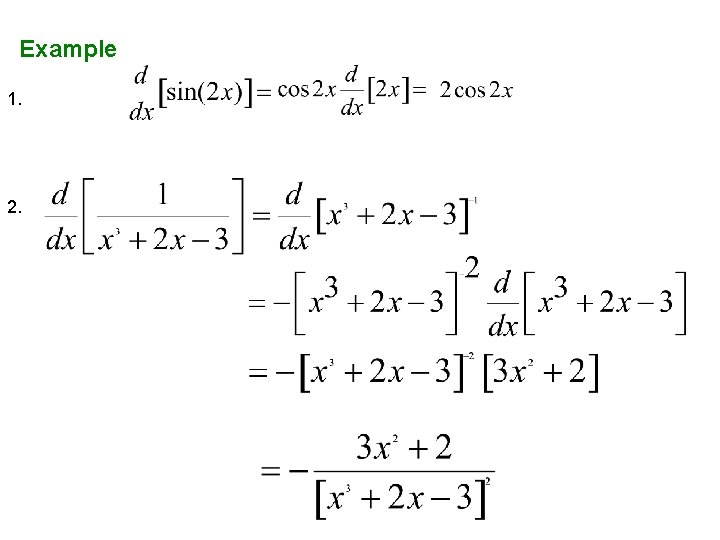
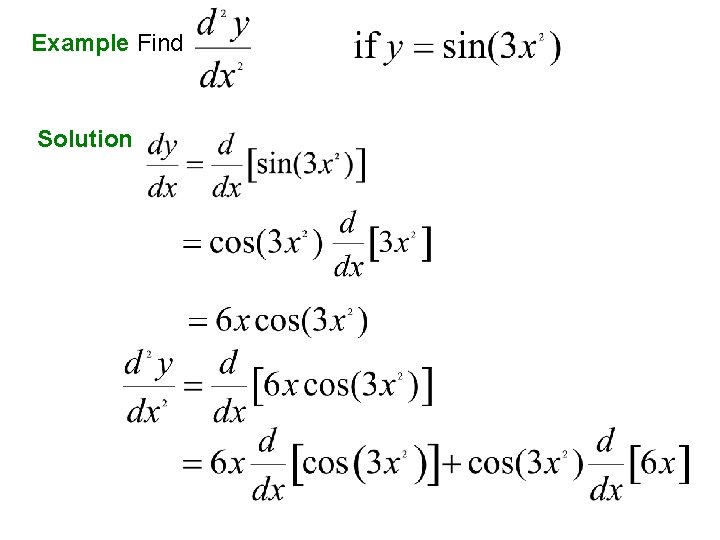











- Slides: 21

MTH 104 Lecture # 9 Calculus and Analytical Geometry

Chain rule Consider multiply rates

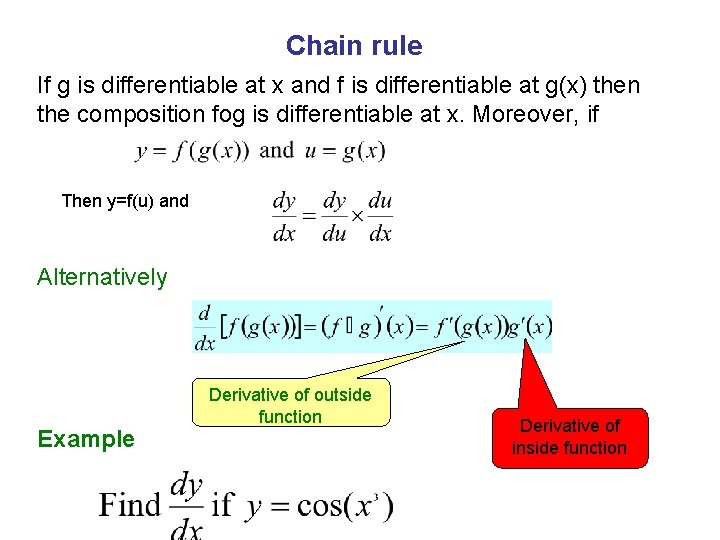
Chain rule If g is differentiable at x and f is differentiable at g(x) then the composition fog is differentiable at x. Moreover, if Then y=f(u) and Alternatively Example Derivative of outside function Derivative of inside function

Let And Rates of change multiply

Example Derivative of outside function Derivative of inside function

More examples Solution 1)


Generalized derivative formulas Some examples are:
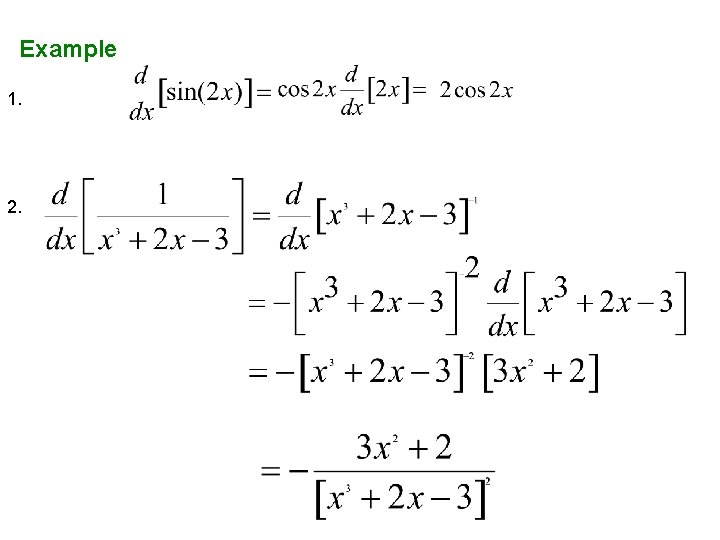
Example 1. 2.
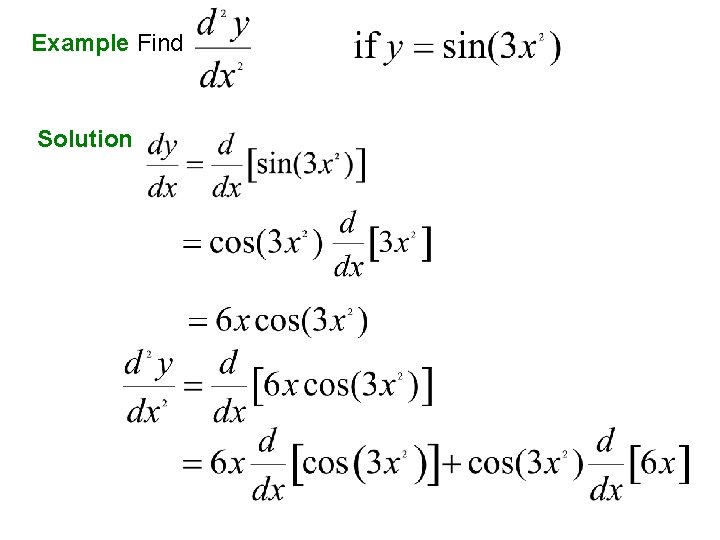
Example Find Solution


Example Differentiate Use the Chain Rule Example Differentiate Use the Quotient Rule

Related rates

Consider a water is draining out of a conical filter. The volume V, the height h and the radius r are all functions of the elapsed time t. Volume formula: Ralated rates problem The rate of change of V is related to the rates of change both r and h

Example Suppose that x and y are differentiable functions of t and are related by the equation. Find dy/dt at time t=1 if x=2 and dx/dt=4 at time t=1. solution Differentiating both sides with respect to t

Example Suppose x and y are both differentiable functions of t and are related by the equation y = x 2 + 3. Find dy/dt, given that dx/dt = 2 when x = 1 Solution Given dx/dt = 2 when x = 1 y = x 2 + 3 To find dy/dt

Procedure for solving related rates problems Step 1. Assign letters to all quantities that vary with time and any others that seem relevant to the problem. Give a definition for each letter. Step 2. Identify the rates of change that are known and the rates of change that is to be found. Interpret each rate as a derivative. Step 3. Find an equation that relates the variables whose rates of change were identified in Step 2. To do this, it will often be helpful to draw an appropriately labeled figure that illsutrates the relationship. Step 4. Differentiate both sides of the equation obtained in Step 3 with respect to time to produce a relationship between the known rates and the unknown rates of change. Step 5. After completing Step 4, substitute all known values for the rates of change and the variables, and then solve for the unknown rate of change.

Example Suppose that , where both x and y are changing with time. At a certain instant when x=1 and y=2, x is decreasing at the rate of 2 units/s, and y is increasing at the rate of 3 units/s. How fast is z changing at this instant? Is z increasing or decreasing? solution Differentiating with respect to t

Negative sign shows that it is decreasing

Example A stone is dropped into a still pond sends out a circular ripple whose radius increases at a constant rate of 3 ft/s. How rapidly is the area of enclosed by the ripple increases at the end of 10 s? Solution let r= radius of circular ripple, A= Area enclosed by the ripple Since radius is increasing with a constant rate of 3 ft/s, so after 10 s the radius will be 30 ft. We know that

 Calculus with analytic geometry examples
Calculus with analytic geometry examples Mth 210
Mth 210 Mth 685
Mth 685 Mth 685
Mth 685 Mth 685
Mth 685 Mth 105
Mth 105 Mth
Mth Mth 210
Mth 210 Father of analytical geometry
Father of analytical geometry Coordinate geometry formula
Coordinate geometry formula 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Pf3 number of vsepr electron groups
Pf3 number of vsepr electron groups 4 electron domains 2 lone pairs
4 electron domains 2 lone pairs The basis of the vsepr model of molecular bonding is
The basis of the vsepr model of molecular bonding is Apple notes
Apple notes Programa 104
Programa 104 Lativ 104
Lativ 104 Odette building 104
Odette building 104 Who is this
Who is this Opw 687
Opw 687 Gg-104
Gg-104 Cct 104
Cct 104