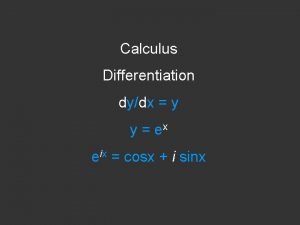Calculus Differentiation Calculus Differentiation dydx y Calculus Differentiation



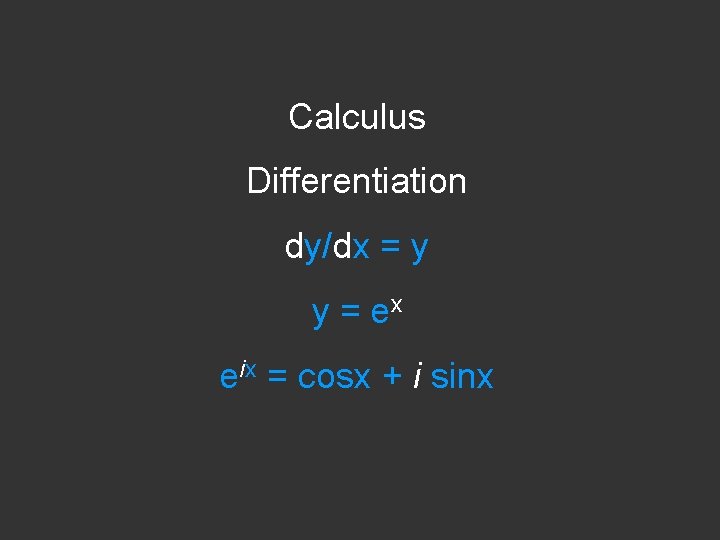

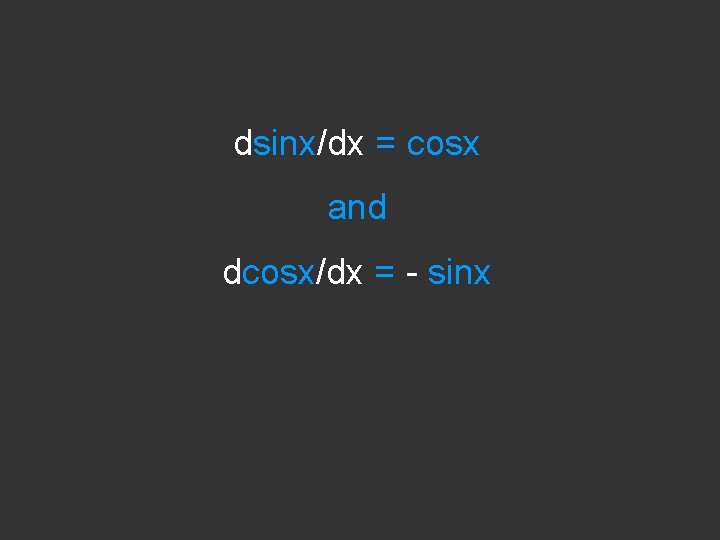
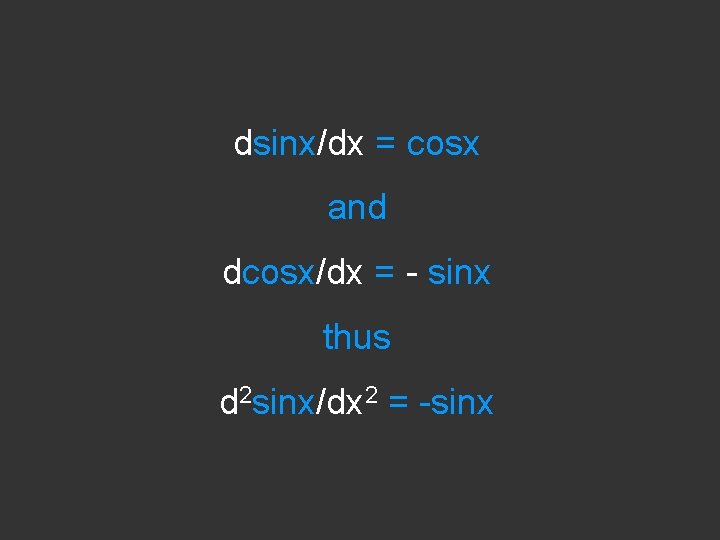

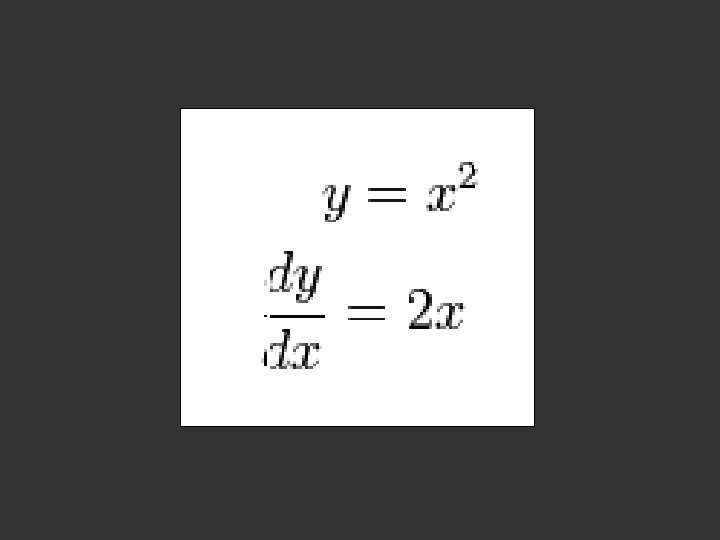
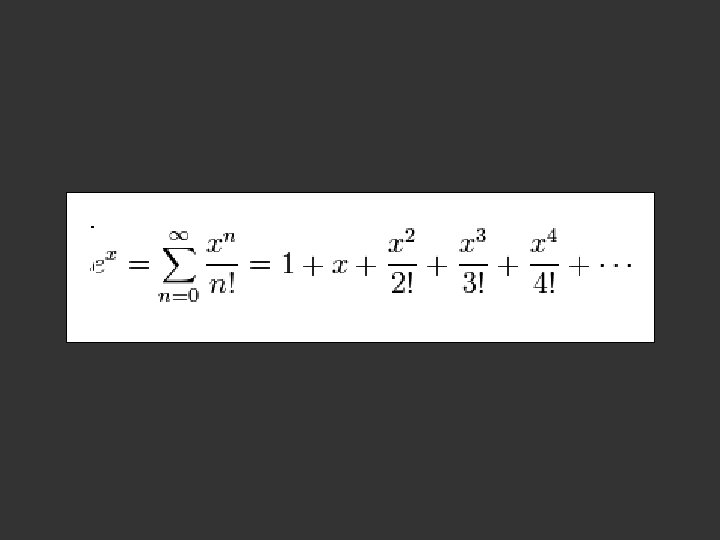

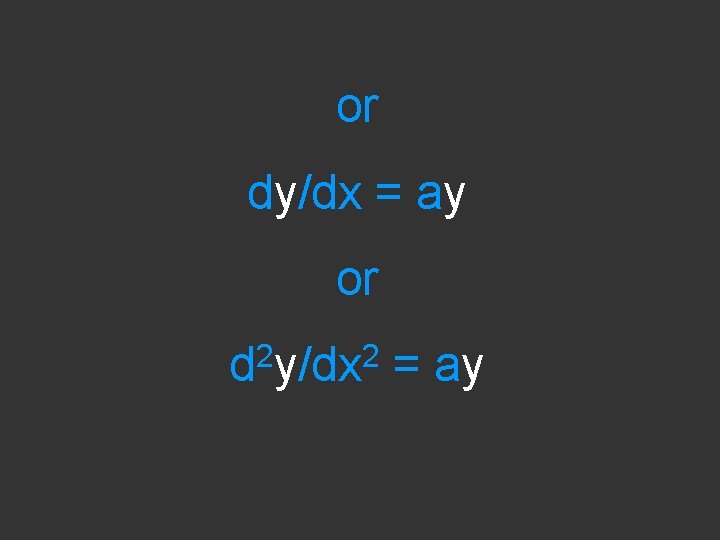








- Slides: 29

Calculus Differentiation

Calculus Differentiation dy/dx = y

Calculus Differentiation dy/dx = y y = ex
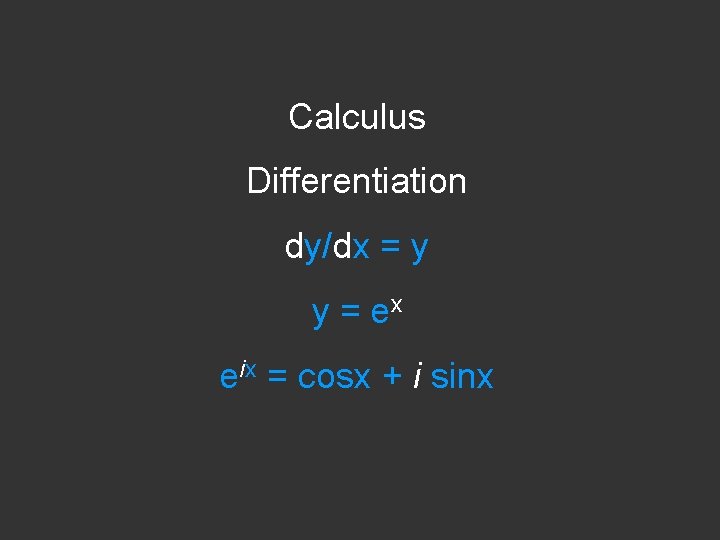
Calculus Differentiation dy/dx = y y = ex eix = cosx + i sinx

dsinx/dx = cosx
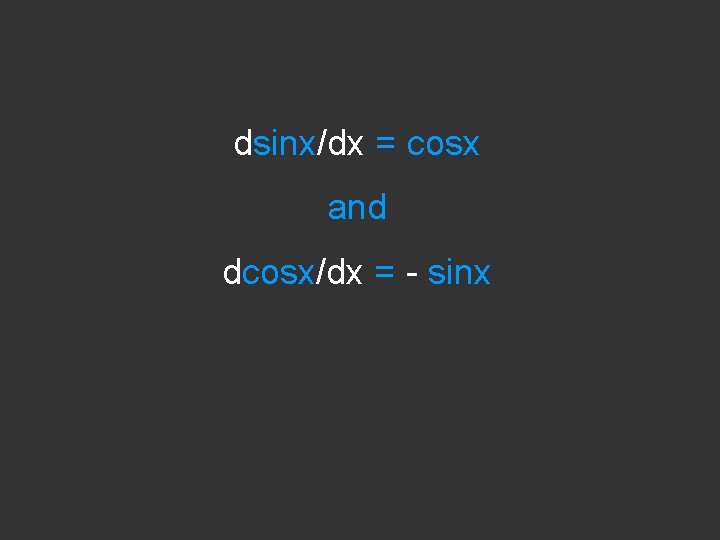
dsinx/dx = cosx and dcosx/dx = - sinx
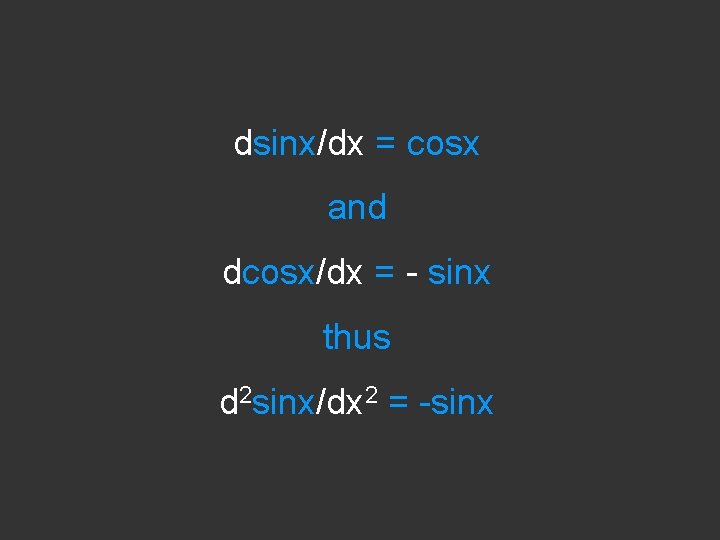
dsinx/dx = cosx and dcosx/dx = - sinx thus d 2 sinx/dx 2 = -sinx

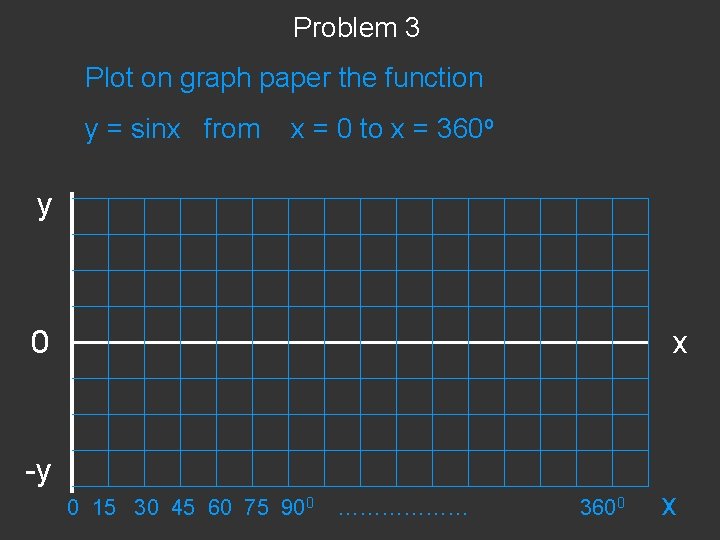
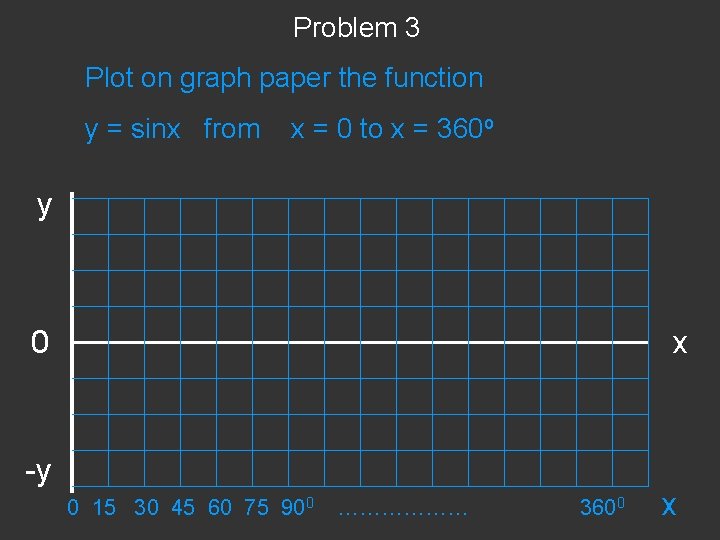
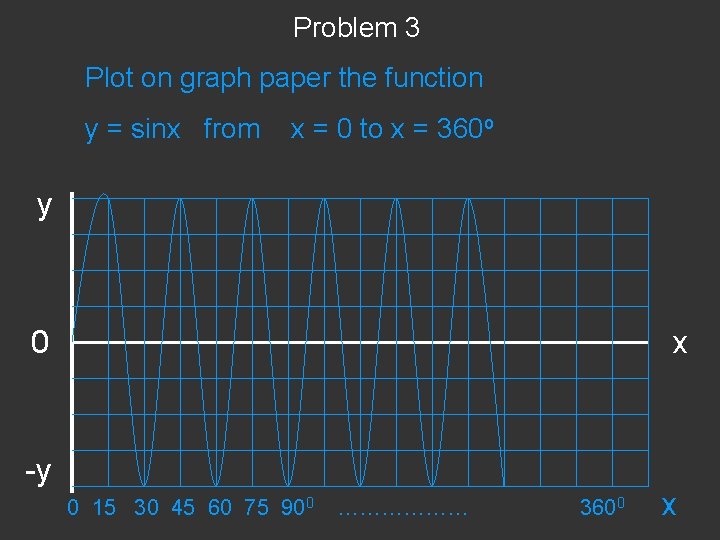
Problem 3 Plot on graph paper the function y = sinx from x = 0 to x = 360 o y 0 -y x 0 15 30 45 60 75 900 ……………… 3600 x

Problem 3 Plot on graph paper the function y = sinx from x = 0 to x = 360 o y 0 -y x 0 15 30 45 60 75 900 ……………… 3600 x


The simplest operation in differential calculus
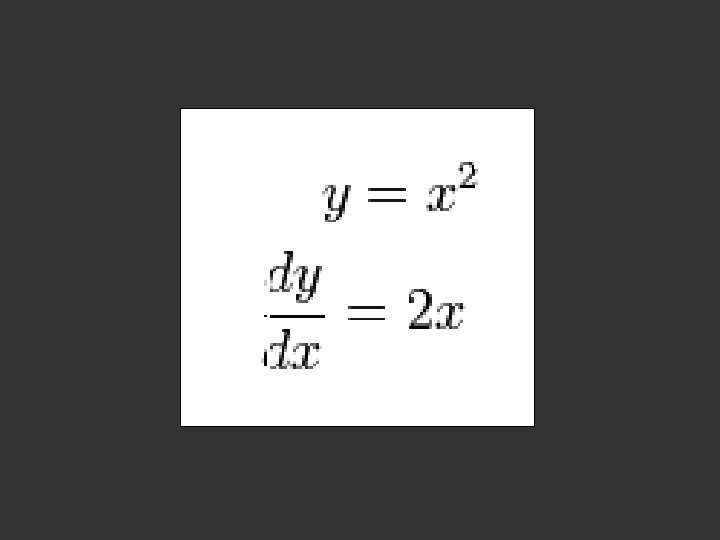
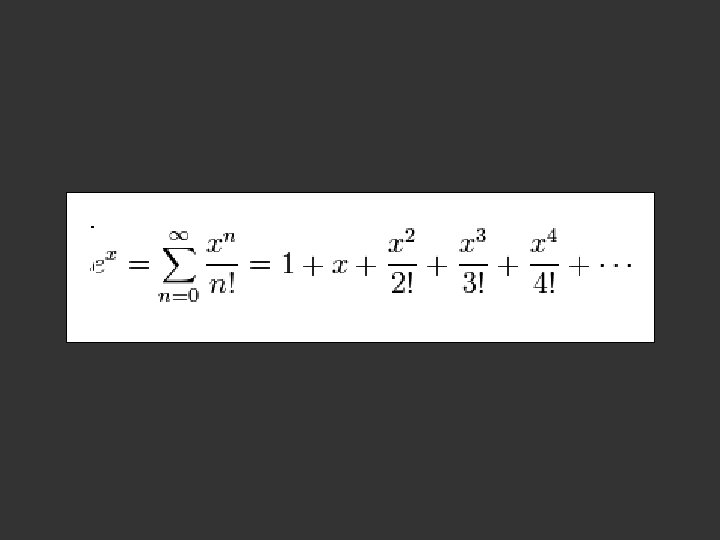

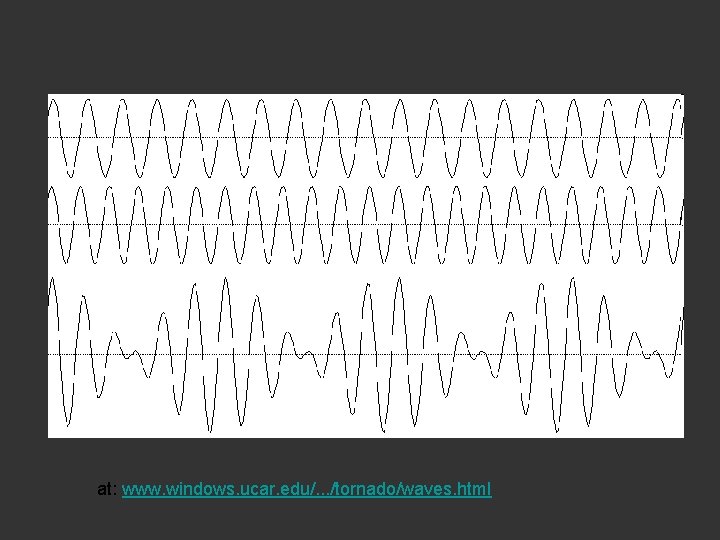
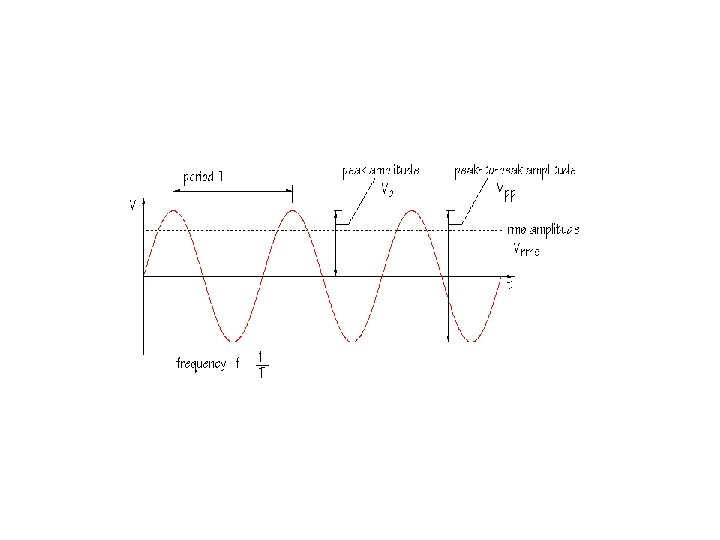
When you see e ……. think WAVES x e at: thestewscope. wordpress. com/2009/07/
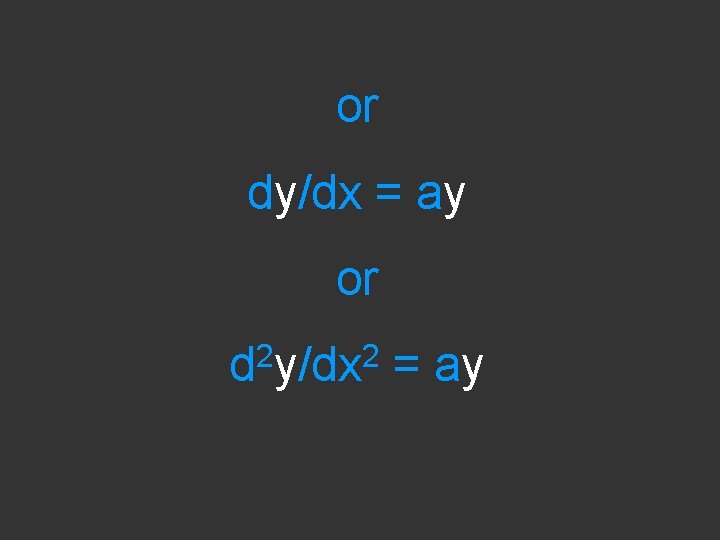
or dy/dx = ay or 2 2 d y/dx = ay

at: zaksiddons. wordpress. com/. . . /

dxn/dx = nxn-1 http: //en. wikipedia. org/wiki/Taylor_series


at: www. windows. ucar. edu/. . . /tornado/waves. html

image at: www. physics. utoronto. ca/. . . /lec 05/index. htm e at: thestewscope. wordpress. com/2009/07/

The Taylor series for the exponential function ex at a = 0 is The above expansion holds because the derivative of ex with respect to x is also ex and e 0 equals 1. This leaves the terms (x − 0)n in the numerator and n! in the denominator for each term in the infinite sum. dxn/dx = nxn-1 http: //en. wikipedia. org/wiki/Taylor_series

Leibniz notation Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real number

Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example:

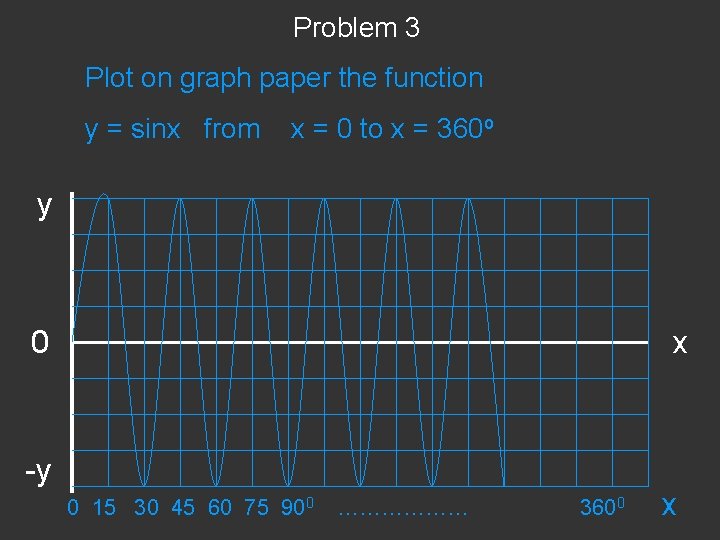
Problem 3 Plot on graph paper the function y = sinx from x = 0 to x = 360 o y 0 -y x 0 15 30 45 60 75 900 ……………… 3600 x

Problem 3 Plot on graph paper the function y = sinx from x = 0 to x = 360 o y 0 -y x 0 15 30 45 60 75 900 ……………… 3600 x




E ρ i B ε o J D μ o c H M P = = = Symbols Electric field charge density electric current Magnetic field permittivity current density Electric displacement permeability speed of light Magnetic field strength Magnetization Polarization
 Stata plot interaction effects
Stata plot interaction effects Implicit derivative matlab
Implicit derivative matlab Fundamental theorem of vector calculus
Fundamental theorem of vector calculus Trigo
Trigo Calculus
Calculus Variational calculus
Variational calculus Curl calculus
Curl calculus Derivative of abc
Derivative of abc Flipped math calculus
Flipped math calculus Diff rule
Diff rule Tijdscomplexiteit
Tijdscomplexiteit Rectilinear motion calculus
Rectilinear motion calculus 2nd fundamental theorem of calculus
2nd fundamental theorem of calculus Persamaan fungsi
Persamaan fungsi Street calculus
Street calculus Relational algebra to tuple relational calculus
Relational algebra to tuple relational calculus Liate calculus
Liate calculus Integral symmetry
Integral symmetry Chapter 2 limits and continuity
Chapter 2 limits and continuity Theories of calcification
Theories of calcification Newton magna
Newton magna Reciprocal rule differentiation
Reciprocal rule differentiation Lambda calculus
Lambda calculus Lvm calculus
Lvm calculus Curve calculus
Curve calculus Mram calculus
Mram calculus Stochastic calculus
Stochastic calculus Gingival index loe and silness
Gingival index loe and silness Calculus crash course
Calculus crash course Physics
Physics