Variation and weighted residual formulation Chapter 2 General

Variation and weighted residual formulation Chapter 2

General concepts • Governing equation inΩ • Boundary condition • Approximate solution : • Ni(x) is the basis or trial function that must satisfy the BCs • R is amount of error or residual • The better approximation, the lower error or residual • Better accuracy could be obtain by higher order approximation • Better accuracy could be obtain by using more basis functions

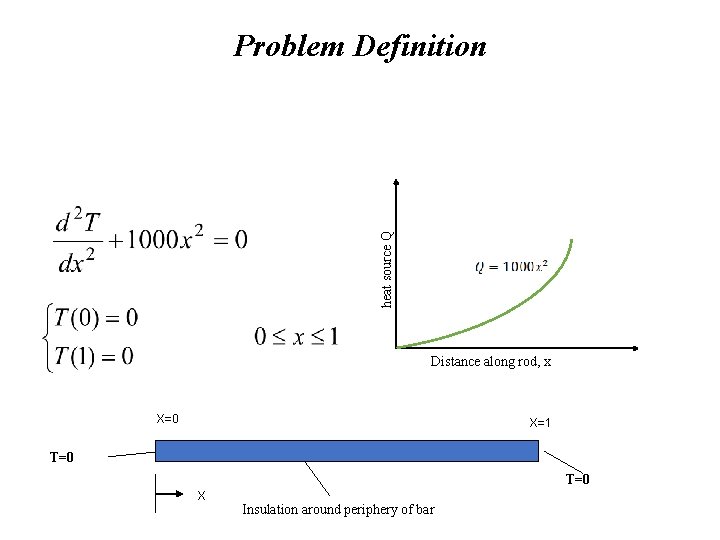
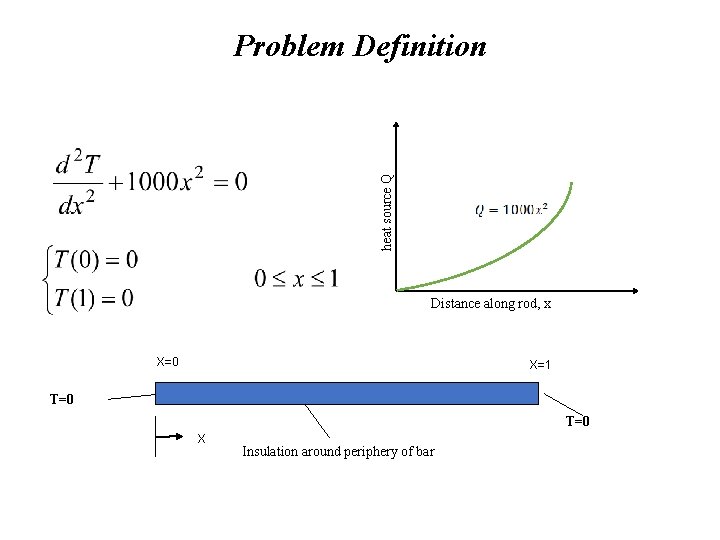
heat source Q Problem Definition Distance along rod, x X=0 X=1 T=0 X Insulation around periphery of bar

The variational method We try to find a function T(x) that minimizes or maximized integrals of The variational formulation of the problem in example (4 -1) become

The variational method v. The idea is to find the function T(x) that extremizes I v. The function T(x) satisfies the original differential equation and boundary conditions v the variational form may be used to obtain solutions to problems that are not readily admitted by the differential formulation v. The variational formulation of a physical problem is often referred to as the weak formulation

Example : • Solving problem posed in the given example by the variational method • Solution • If a mimimum has been found • If a maximum has been found

Example :

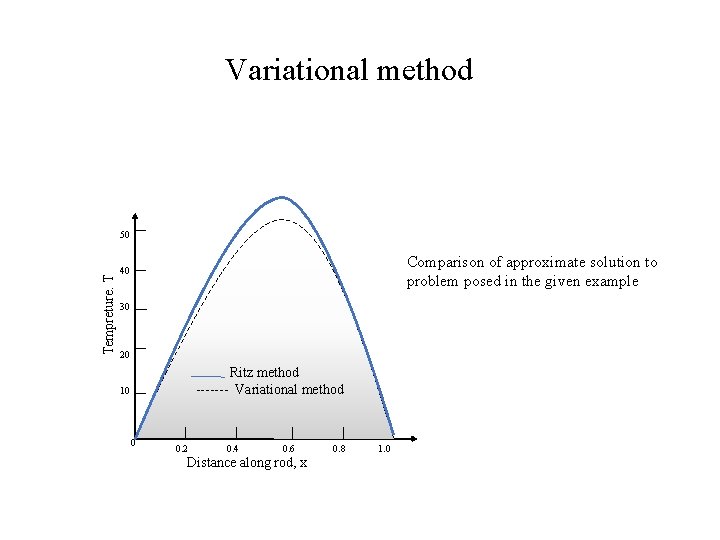
Variational method Tempreture. T 50 Comparison of approximate solution to problem posed in the given example 40 30 20 Ritz method ------- Variational method 10 0 0. 2 0. 4 0. 6 Distance along rod, x 0. 8 1. 0

Variational calculus v. The weighted- residual methods are far easier to apply and can be used even when no variational formulation exists v. All variational formulation have a corresponding differential formulation, but, unfortunately , the converse is not true: some differential formulation have no classical variational principle

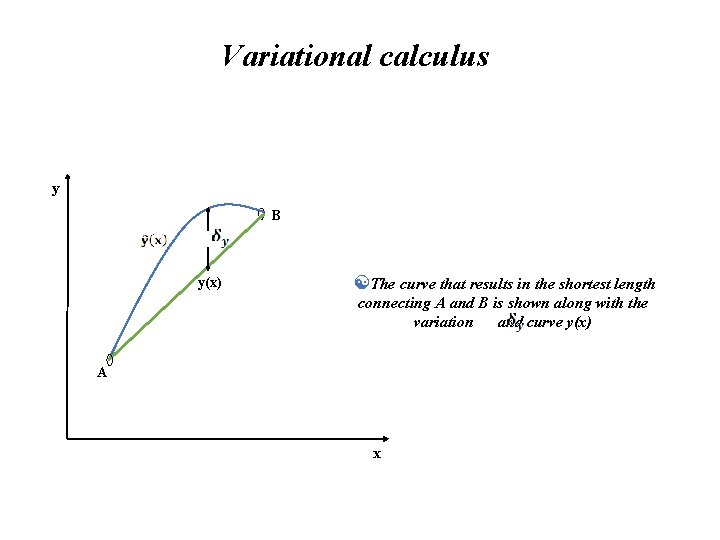
Variational calculus y B y(x) The curve that results in the shortest length connecting A and B is shown along with the variation and curve y(x) A x

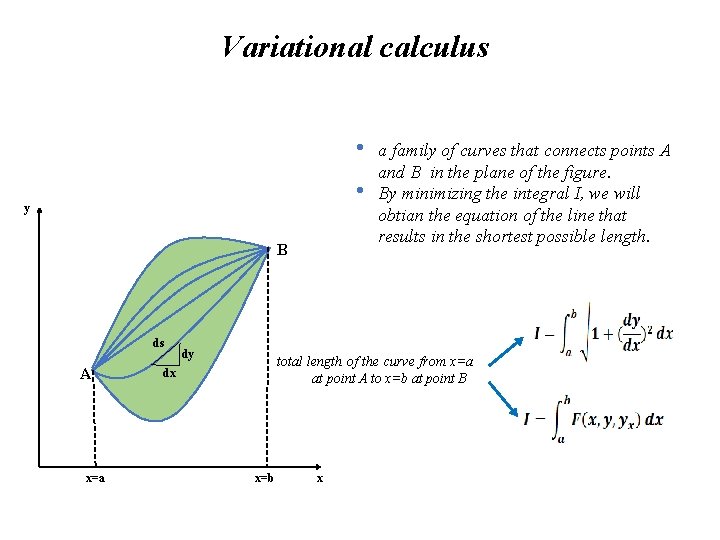
Variational calculus • The shortest curve that connects two given points • First, we must set an integral I that represents the length of the curve. • An element are length ds from the phythagorean theorem is given by

Variational calculus • • y B ds A x=a dy a family of curves that connects points A and B in the plane of the figure. By minimizing the integral I, we will obtian the equation of the line that results in the shortest possible length. total length of the curve from x=a at point A to x=b at point B dx x=b x

Variational calculus • Function F must satisfy the following differential equation:

Variational calculus By using the boundary conditions:

Integration by parts Taylor’s series

The differential of a function Variation of a function F(x, y, yx) , δx=0

The commutative properties The commutative property of differentiation and variation operators Another commutative property is

Miscellaneous Rules of variational calculus • Y and z be any continuous and differentiable functions.

THE EULER-LAGRANGE EQUATION GEOMETRIC AND NATURAL BOUDARY CONDITIONS • The necessary condition for the existence of an extremum of the functional • Is that its first variation must be zero, or

THE EULER-LAGRANGE EQUATION: GEOMETRIC AND NATURAL BOUDARY CONDITIONS §Rewrite §Therefore becomes

THE EULER-LAGRANGE EQUATION: GEOMETRIC AND NATURAL BOUDARY CONDITIONS • Fixed boundary conditions • Natural boundary conditions EULER-LAGRANGE EQUATION

Example : Variational formulation for the given differential equation • For the problem posed in example 4 -1, show that the functional to be extremized § solution

Example : • The value of T is to be held fixed at either end of the interval , the variation of T or must be zero at these two point • Condition T(0)=0 and T(1)=0, since at these points. This type of boundary condition is referred to as a geometric boundary condition • When on the boundary, we have a natural boundary condition.

Example : Variational formulation for the given differential equation (1)

Example : Variational formulation for the given differential equation (2) v. By starting with v. For the problem stated in example 4 -1 drive I

solution v. This may be broken into two separate integrals to give:

solution

solution • We have T=0 at x=0 x=1 • Could be satisfied is when d. T/dx is zero on the boundaries, i. e. , at x=0 and x=1 in this problem. • d. T/dx is zero when insulation is present. • The condition that ∂F/∂Tx is also referred to as a natural boundary condition

Euler-Lagrange equation § The Euler-Lagrange equation was introduced for the class of problems whose functional F providing we also satisfy

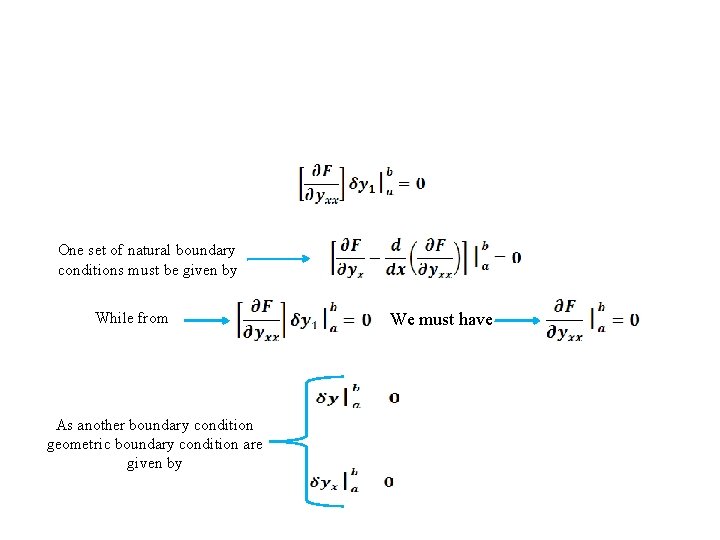
One set of natural boundary conditions must be given by While from As another boundary condition geometric boundary condition are given by We must have

Variational formulations exist for only those problems whose differential formulations do not contain odd-ordered derivatives

Weighted Residuals

General concepts of weighted residuals § Governing equation : § Boundary conditions :

General concepts of weighted residuals Unknown (but constant) parameters Trial function arbitrary weighting function

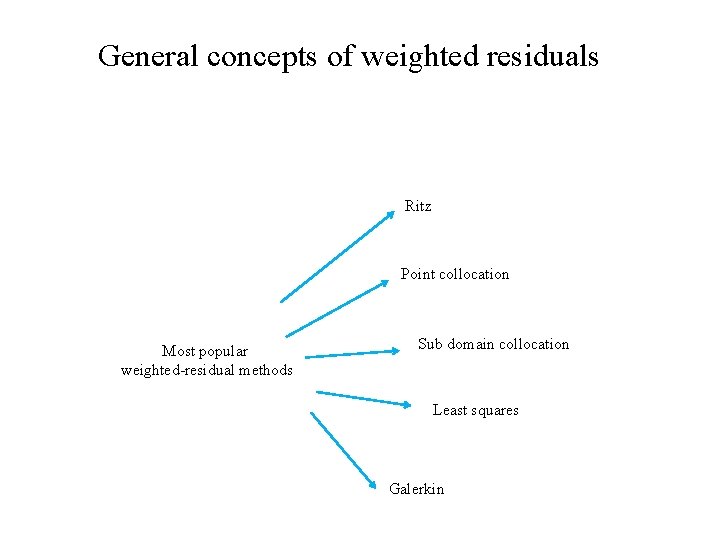
General concepts of weighted residuals Ritz Point collocation Most popular weighted-residual methods Sub domain collocation Least squares Galerkin

heat source Q Problem Definition Distance along rod, x X=0 X=1 T=0 X Insulation around periphery of bar

Types of Boundary conditions: If maximum order of derivatives in a given equation is m • Essential B. C. with order n • Non-Essential B. C. with order n

The ritz method • R is the residual or error Satisfy the essential boundary condition • Trial (basis) function Does not grossly violate the physics of problem

The ritz method the first – order approximation T:

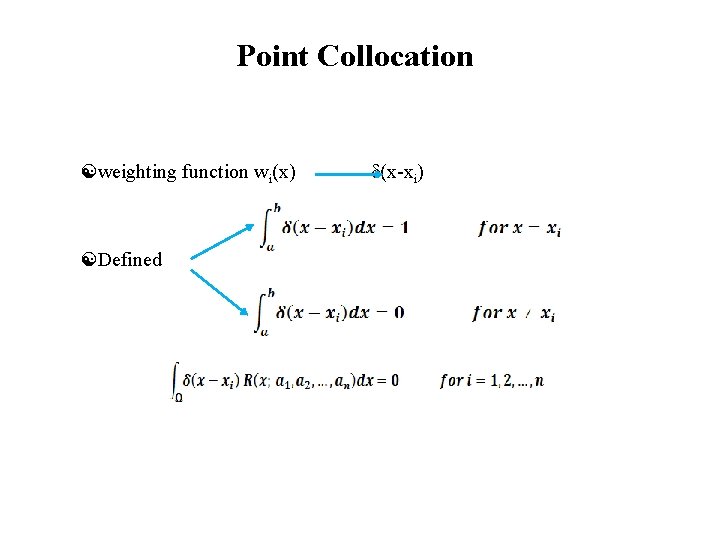
Point Collocation weighting function wi(x) Defined (x-xi)

Point Collocation

Example : • Using the trial function assumed in example 4 -1, determine an approximate solution to the problem posed in that example by the point collocation method Only one trail function is used • Solution Only one parameter(namely, a 1) Choose the collocation point x 1 to be in the middle of the domain, or x 1=1/2

Example : Must evaluate this residual at the collocation point or at x 1=1/2 and set the result to zero, or Solving for a 1 Number of unknown parameters must be equal to the number of collocation points

Subdomain Collocation • the weighting functions are chosen to be unity over a portion of the domain and zero elsewhere. Mathematically, the wi(x) are given by

Subdomain Collocation N integral equations The different integration domains should be noted Number of unknowns must be equal to number of integrals or number of subdomains

Subdomain Collocation weighted-residual method for three subdomains w 3 (x) 1 w 2 (x) 0 x 1 0 w 1 (x) Ω 1 Ω 2 x 1 0 Ω Ω 3 x

Example : • Repeat example 4 -1 by using the subdomain collocation method with the same trial function • Since only one parameter is unknown so only one domain must be used which is Ω=[0 1]

Least Squares The method of least squares requires that the integral I of the square of the residual R be minimized. the integral I is given by

Least Squares

Least Squares

Example : Resolve (approximately) the problem in example 4 -1 by using the leastsquares method and the same trail function There is only one unknown parameter a 1

Example :

Galerkin The trial functions Ni(x) themselves are used as the weighting function or

Example : • Resolve given problem by galerkin method and same trial function Trial function

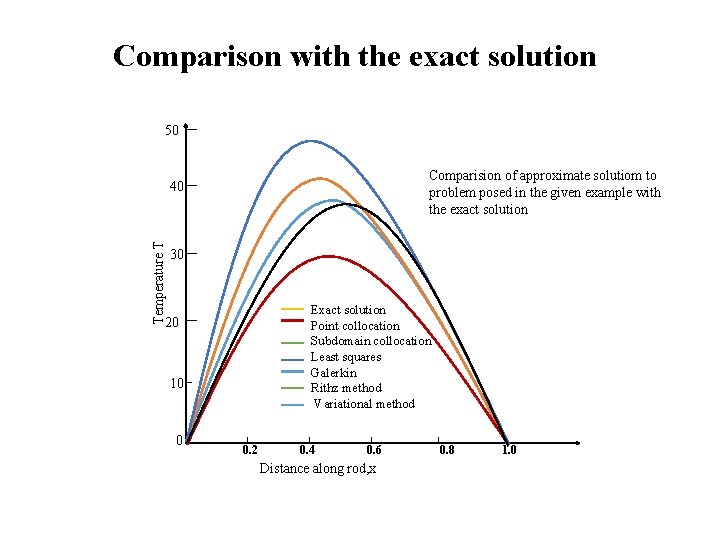
Comparison with the exact solution If given problem solved exactly The approximate solution from the Ritz method (example 4 -1) is identical to that obtained from subdomain collocation. Similarly, the variational and Galerkin solution are identical. None of the methods seems to do a particularly outstanding job of approximating the exact solution

Comparison with the exact solution 50 Comparision of approximate solutiom to problem posed in the given example with the exact solution Temperature T 40 30 Exact solution Point collocation Subdomain collocation Least squares Galerkin Rithz method Variational method 20 10 0 0. 2 0. 4 0. 6 Distance along rod, x 0. 8 1. 0

Example : Minimum Potential energy • Find approximate deformation function for the given elastic one dimensional rod.

Example : Galerkin • Find approximate deformation function for the given elastic one dimensional rod.

Example : Galerkin

Example 3 : Minimum Potential Energy n Find approximate elongation function for the given elastic one dimensional rod, using linear approximation. x L, E, A F

Ritz method : • Find approximate elongation function for the given elastic one dimensional rod, using linear basis functions. x L, E, A F

Example : Minimum Potential Energy • Find approximate elongation function for the given elastic one dimensional rod, using quadratic approximation. x L, E, A F

Example : Minimum Potential Energy • Find approximate elongation function for the given elastic one dimensional rod, using two basis functions. x L, E, A F

Example : Galerkin • Find approximate elongation function for the given elastic one dimensional rod, using two basis functions. x L, E, A F