DIRECT VARIATION DIRECT VARIATION DIRECT VARIATION When one

DIRECT VARIATION

DIRECT VARIATION

DIRECT VARIATION When one thing gets larger, the other gets larger.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example:

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this:

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this: W is Ando’s weight.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this: W is Ando’s weight. E is the amount Ando eats.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this: W is Ando’s weight. E is the amount Ando eats. K is ALWAYS the constant amount that he gains.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this: W is Ando’s weight. E is the amount Ando eats. K is ALWAYS the constant amount that he gains. K is called the “constant of variation”.

DIRECT VARIATION When one thing gets larger, the other gets larger. For Example: The more food Ando eats, the more weight he gains. When the amount of food Ando eats goes up, the amount of weight he gains goes up. As an equation it would look like this: W is Ando’s weight. E is the amount Ando eats. K is ALWAYS the constant amount that he gains. K is called the “constant of variation”. W = KE

DIRECT VARIATION Write a direct variation equation for the following:

DIRECT VARIATION Write a direct variation equation for the following: The cost of postage has a constant price of 30 cents per ounce.

DIRECT VARIATION Write a direct variation equation for the following: The cost of postage has a constant price of 30 cents per ounce. The distance traveled has a constant speed of 30 miles per hour.

DIRECT VARIATION Write a direct variation equation for the following: The cost of postage has a constant price of 30 cents per ounce. The distance traveled has a constant speed of 30 miles per hour. The points scored has a constant amount of 6 per touchdown.

DIRECT VARIATION Write a direct variation equation for the following: The cost of postage has a constant price of 30 cents per ounce. The distance traveled has a constant speed of 30 miles per hour. The points scored has a constant amount of 6 per touchdown. What is the DEPENDENT and INDEPENDENT variable in each equation?

DIRECT VARIATION Write a direct variation equation for the following: The cost of postage has a constant price of 30 cents per ounce. The distance traveled has a constant speed of 30 miles per hour. The points scored has a constant amount of 6 per touchdown. What is the DEPENDENT and INDEPENDENT variable in each equation? What variable represents dependent and what variable represents independent in general?

DIRECT VARIATION: What sort of standard equation rule can you make for direct variations?

DIRECT VARIATION: Manipulating equations:

DIRECT VARIATION: Manipulating equations: Show y = kx me two other ways to write the equation

DIRECT VARIATION Using the information given:

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point:

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5)

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know:

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1)

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1) Solve for k.

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1) Solve for k. k(1) = 5

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1) Solve for k. k(1) = 5 k = 5/1

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1) Solve for k. k(1) = 5 k = 5/1 k=5

DIRECT VARIATION Using the information given: Write a direct variation equation that includes the given point: (1, 5) The general equation is y = kx Put in the information you know: 5 = k(1) Solve for k. k(1) = 5 k = 5/1 k=5 y = 5 x

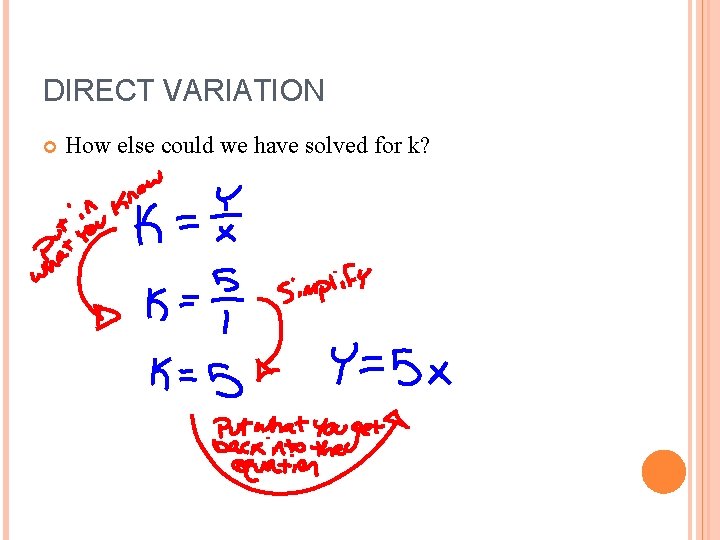
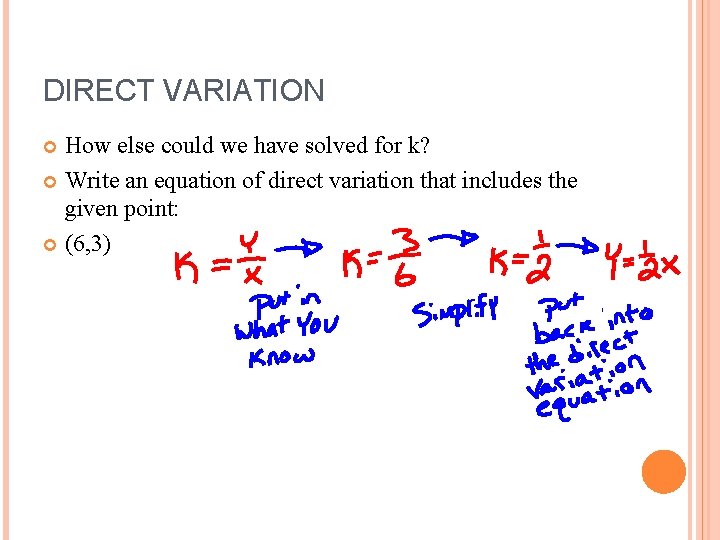
DIRECT VARIATION How else could we have solved for k?

DIRECT VARIATION How else could we have solved for k? Write an equation of direct variation that includes the given point:

DIRECT VARIATION How else could we have solved for k? Write an equation of direct variation that includes the given point: (6, 3)