Digital Design MODULE I CODES WEIGHTED AND NONWEIGHTED

Digital Design MODULE –I CODES: WEIGHTED AND NON-WEIGHTED CODES Amit Kumar Assistant Professor SCSE, Galgotias University, Greater Noida

Outline • Codes • Types of Codes • Weighted • Non-Weighted

Introduction • In the coding, when numbers, letters or words are represented by a specific group of symbols, it is said that the number, letter or word is being encoded. The group of symbols is called as a code. • The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. • The binary code is represented by the number as well as alphanumeric letter.

Advantages of Binary Code Following is the list of advantages that binary code offers. • Binary codes are suitable for the computer applications. • Binary codes are suitable for the digital communications. • Binary codes make the analysis and designing of digital circuits if we use the binary codes. • Since only 0 & 1 are being used, implementation becomes easy.

Classification of Binary Code The codes are broadly categorized into following four categories: • Weighted Codes • Non-Weighted Codes • Binary Coded Decimal Code • Alphanumeric Codes • Error Detecting Codes • Error Correcting Codes

Weighted Codes Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. In these codes each decimal digit is represented by a group of four bits.

Non-Weighted Codes In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code and Gray code.

Binary Coded Decimal (BCD) Systems �The BCD system is employed by computer systems to encode the decimal number into its equivalent binary number. �This is generally accomplished by encoding each digit of the decimal number into its equivalent binary sequence. �The main advantage of BCD system is that it is a fast and efficient system to convert the decimal numbers into binary numbers as compared to the pure binary system.

Binary Coded Decimal (BCD) Systems �The 4 -bit BCD system is usually employed by the computer systems to represent and process numerical data only. In the 4 -bit BCD system, each digit of the decimal number is encoded to its corresponding 4 -bit binary sequence. The two most popular 4 -bit BCD systems are: • Weighted 4 -bit BCD code • Excess-3 (XS-3) BCD code

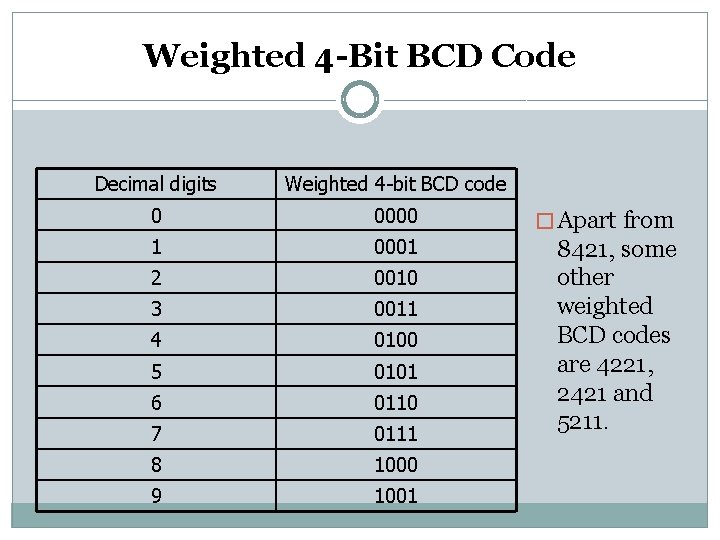
Weighted 4 -Bit BCD Code (8421) � The weighted 4 -bit BCD code is more commonly known as 8421 weighted code. � It is called weighted code because it encodes the decimal system into binary system by using the concept of positional weighting into consideration. � In this code, each decimal digit is encoded into its 4 -bit binary number in which the bits from left to right have the weights 8, 4, 2, and 1, respectively.

Weighted 4 -Bit BCD Code Decimal digits Weighted 4 -bit BCD code 0 0000 � Apart from 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8421, some other weighted BCD codes are 4221, 2421 and 5211. 8 1000 9 1001

Weighted 4 -Bit BCD Code Represent the decimal number 5327 in 8421 BCD code. The corresponding 4 -bit 8421 BCD representation of decimal digit 5 is 0101 The corresponding 4 -bit 8421 BCD representation of decimal digit 3 is 0011 The corresponding 4 -bit 8421 BCD representation of decimal digit 2 is 0010 The corresponding 4 -bit 8421 BCD representation of decimal digit 7 is 0111 Therefore, the 8421 BCD representation of decimal number 5327 is 010100100111.

Advantages & Disadvantage of Binary Code Advantages of BCD Codes • It is very similar to decimal system. • We need to remember binary equivalent of decimal numbers 0 to 9 only. Disadvantages of BCD Codes • The addition and subtraction of BCD have different rules. • The BCD arithmetic is little more complicated. • BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.

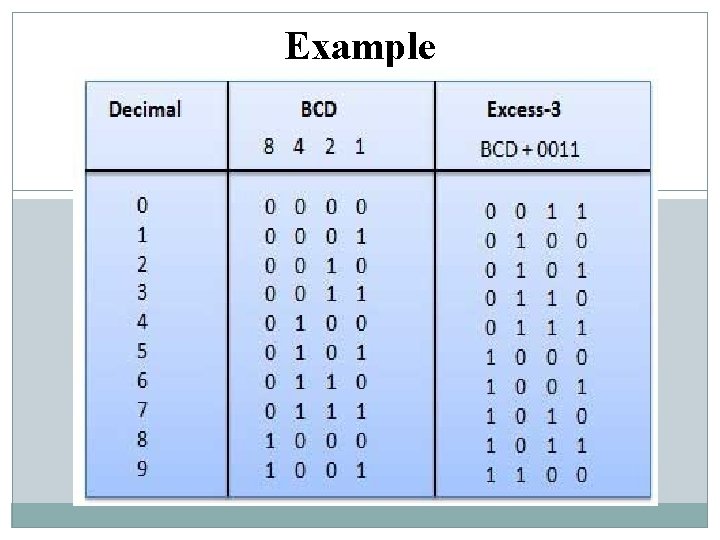
Excess-3 Code • The Excess-3 (XS-3) BCD code does not use the principle of positional weights into consideration while converting the decimal numbers to 4 -bit BCD system. Therefore, we can say that this code is a non-weighted BCD code. • The function of XS-3 code is to transform the decimal numbers into their corresponding 4 -bit BCD code. • In this code, the decimal number is transformed to the 4 -bit BCD code by first adding 3 to all the digits of the number and then converting the excess digits, so obtained, into their corresponding 8421 BCD code. Therefore, we can say that the XS-3 code is strongly related with 8421 BCD code in its functioning.

Excess-3 Code The excess-3 codes are obtained as follows

Example

Excess-3 Code Convert the decimal number 85 to XS-3 BCD code. Add 3 to each digit of the given decimal number as: 8+3=11 5+3=8 The corresponding 4 -bit 8421 BCD representation of the decimal digit 11 is 1011. The corresponding 4 -bit 8421 BCD representation of the decimal digit 8 is 1000. Therefore, the XS-3 BCD representation of the decimal number 85 is 1011 1000.

The Gray Code 18 § Unweighted (not an arithmetic code). § Only a single bit change from one code number to the § next. Good for error detection.

The Gray Code 19 0000 0001 0011 0001 0010 0000 0010 0111 0011 0101 0001 0100 0000 1100 0101 1101 0111 1111 0110 1110 0010 1010 0011 1011 0001 1001 0000 1000 Generating 4 -bit standard Gray code.

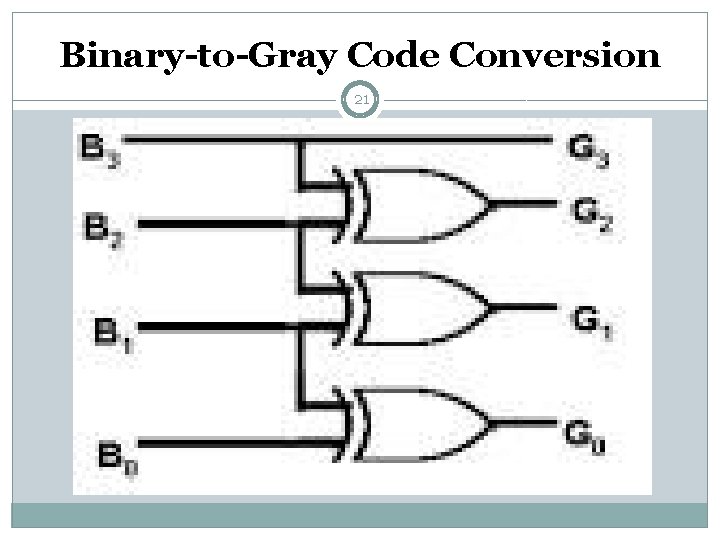
Binary-to-Gray Code Conversion 20 § Retain most significant bit. § From left to right, add each adjacent pair of binary code § bits to get the next Gray code bit, discarding carries. Example: Convert binary number 10110 to Gray code. (10110)2 = (11101)Gray

Binary-to-Gray Code Conversion 21

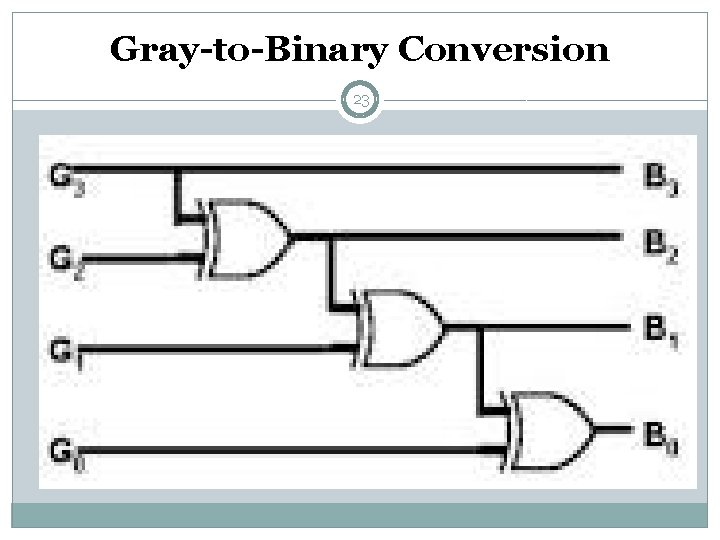
Gray-to-Binary Conversion 22 § Retain most significant bit. § From left to right, add each binary code bit generated to § the Gray code bit in the next position, discarding carries. Example: Convert Gray code 11011 to binary. (11011)Gray = (10010)2

Gray-to-Binary Conversion 23

Application of Gray code 24 �Gray code is popularly used in the shaft position encoders. �A shaft position encoder produces a code word which represents the angular position of the shaft.

Self-Complementing Codes 25 § Examples: excess-3, 84 -2 -1, 2*421 codes. § The codes that represent the pair of complementary digits are complementary of each other. Excess-3 code 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 241: 0101 0111 0100 758: 1010 1000 1011

Alphanumeric Codes 26 § Apart from numbers, computers also handle textual data. § Character set frequently used includes: alphabets: ‘A’. . ‘Z’, and ‘a’. . ‘z’ digits: ‘ 0’. . ‘ 9’ special symbols: ‘$’, ‘, ’, ‘@’, ‘*’, … non-printable: SOH, NULL, BELL, … § Usually, these characters can be represented using 7 or 8 bits.

Alphanumeric Codes 27 § ASCII: 7 -bit, plus a parity bit for error detection (odd/even parity).

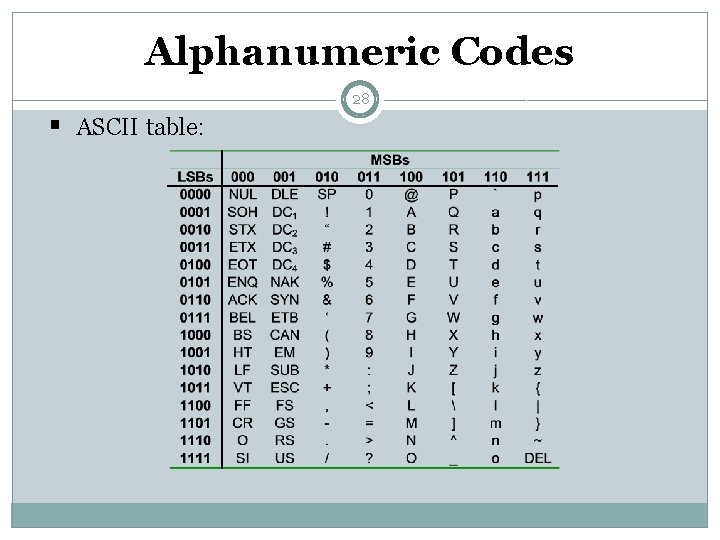
Alphanumeric Codes 28 § ASCII table:

Error Detection Codes 29 § Errors can occur data transmission. They should be detected, so that re-transmission can be requested. § With binary numbers, usually single-bit errors occur. Example: 0010 erroneously transmitted as 0011, or 0000, or 0110, or 1010. § Biquinary code uses 3 additional bits for errordetection. For single-error detection, one additional bit is needed.

Error Detection Codes 30 § Parity bit. v Even parity: additional bit supplied to make total number of ‘ 1’s even. v Odd parity: additional bit supplied to make total number of ‘ 1’s odd. § Example: Odd parity. Parity bits

Error Detection Codes 31 § Parity bit can detect odd number of errors but not even number of errors. Example: For odd parity numbers, 10011 10001 (detected) 10011 10101 (non detected) § Parity bits can also be applied to a block of data: Column-wise parity Row-wise parity

Error Detection Codes 32 § Sometimes, it is not enough to do error detection. We may want to do error correction. § Error correction is expensive. In practice, we may use only single-bit error correction. § Popular technique: Hamming Code.