Implicit Differentiation However some functions are defined implicitly






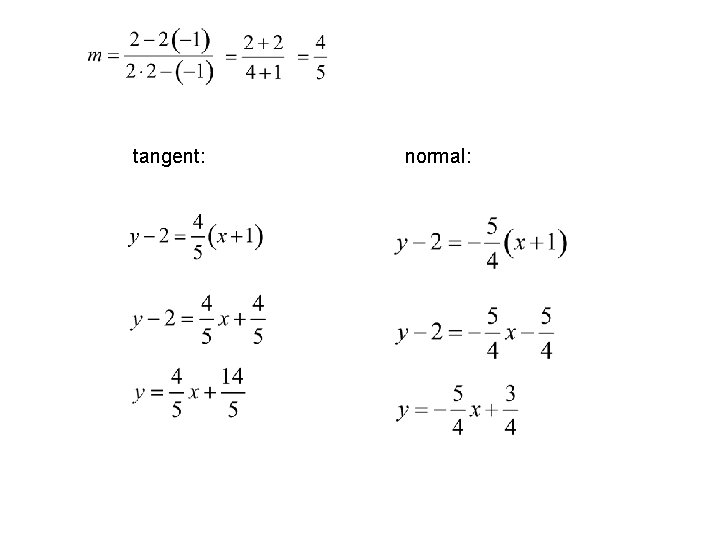



- Slides: 12

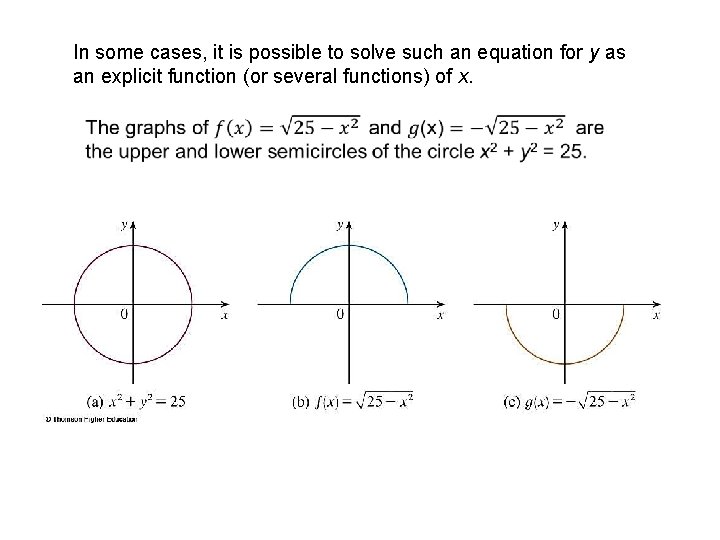
Implicit Differentiation However, some functions are defined implicitly. Some examples of implicit functions are: x 2 + y 2 = 25 x 3 + y 3 = 6 xy

In some cases, it is possible to solve such an equation for y as an explicit function (or several functions) of x.

Nonetheless, x 3 + y 3 = 6 xy is the equation of a curve called the folium of Descartes shown here and it implicitly defines y as several functions of x. It’s not easy to solve equation x 3 + y 3 = 6 xy for y explicitly as a function of x by hand. A computer algebra system has no trouble. However, the expressions it obtains are very complicated Fortunately, we don’t need to solve an equation for y in terms of x to find the derivative of y. Instead, we can use the method of implicit differentiation. This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. In the examples, it is always assumed that the given equation determines y implicitly as a differentiable function of x so that the method of implicit differentiation can be applied.

example: a. Differentiate both sides of the equation x 2 + y 2 = 25: At the point (3, 4) we have x = 3 and y = 4. Thus, an equation of the tangent to the circle at (3, 4) is: y – 4 = – ¾(x – 3) or 3 x + 4 y = 25.

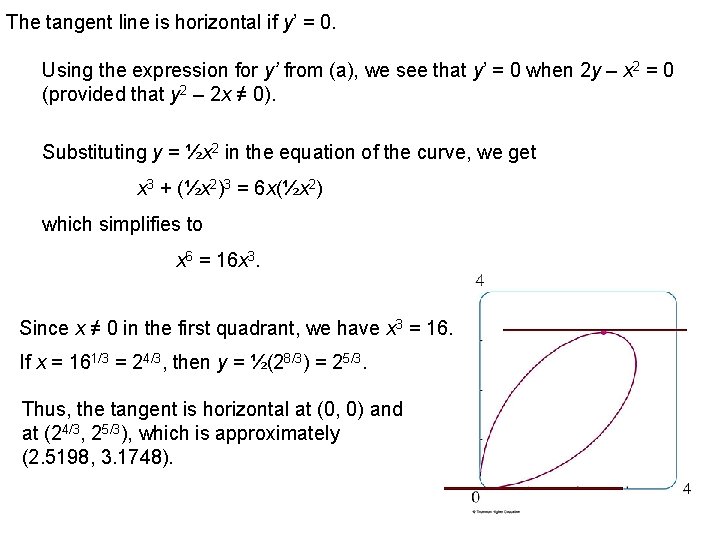
example: a. Find y’ if x 3 + y 3 = 6 xy. b. Find the tangent to the folium of Descartes x 3 + y 3 = 6 xy at the point (3, 3). c. At what points in the first quadrant is the tangent line horizontal? Differentiating both sides of x 3 + y 3 = 6 xy with respect to x, regarding y as a function of x, and using the Chain Rule on y 3 and the Product Rule on 6 xy, we get: 3 x 2 + 3 y 2 y’ = 6 xy’ + 6 y or x 2 + y 2 y’ = 2 xy’ + 2 y Now, we solve for y’: When x = y = 3, y’ = – 1 So, an equation of the tangent to the folium at (3, 3) is: y – 3 = – 1(x – 3) or x + y = 6.

The tangent line is horizontal if y’ = 0. Using the expression for y’ from (a), we see that y’ = 0 when 2 y – x 2 = 0 (provided that y 2 – 2 x ≠ 0). Substituting y = ½x 2 in the equation of the curve, we get x 3 + (½x 2)3 = 6 x(½x 2) which simplifies to x 6 = 16 x 3. Since x ≠ 0 in the first quadrant, we have x 3 = 16. If x = 161/3 = 24/3, then y = ½(28/3) = 25/3. Thus, the tangent is horizontal at (0, 0) and at (24/3, 25/3), which is approximately (2. 5198, 3. 1748).

This can’t be solved for y.

example: Find the equations of the lines tangent and normal to the curve at at We need the slope. Since we can’t solve for y, we use implicit differentiation to solve for y’. Note product rule.
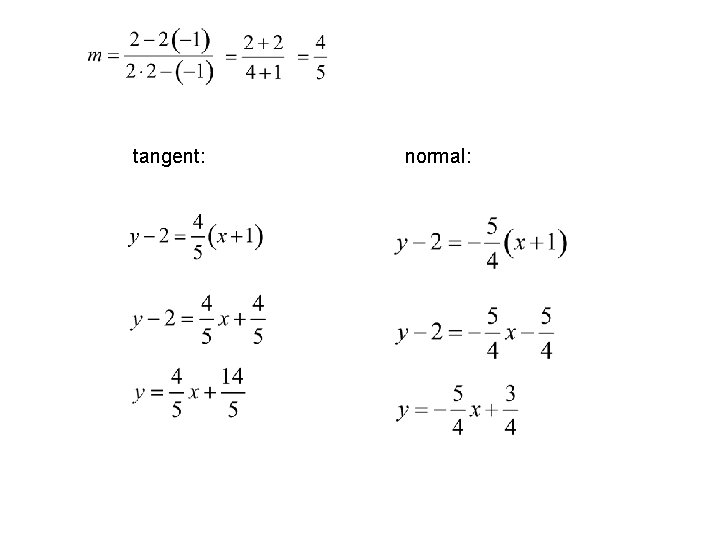
tangent: normal:

Higher Order Derivatives Find if Substitute back into the equation.

example: Find y” if x 4 + y 4 = 16. Differentiating the equation implicitly with respect to x, we get 4 x 3 + 4 y 3 y’ = 0. To find y’’, we differentiate this expression for y’ using the Quotient Rule and remembering that y is a function of x:

However, the values of x and y must satisfy the original equation x 4 + y 4 = 16. So, the answer looks quite simple:
 Implicitly defined functions
Implicitly defined functions Implicit function grapher
Implicit function grapher Insidan region jh
Insidan region jh Implicit differentiation with inverse trig functions
Implicit differentiation with inverse trig functions Does although need a comma
Does although need a comma Implicit differentiation formula
Implicit differentiation formula Rules of implicit differentiation
Rules of implicit differentiation Implicit differentiation
Implicit differentiation Implicit differentiation vs chain rule
Implicit differentiation vs chain rule Explicit differentiation
Explicit differentiation Derivatives of a function
Derivatives of a function Implicit partial differentiation
Implicit partial differentiation Explicit vs implicit equation
Explicit vs implicit equation


















